day49【代码随想录】动态规划之最长公共子序列、不相交的线、最大子序和、判断子序列
文章目录
- 前言
- 一、最长公共子序列(力扣1143)
- 二、不相交的线(力扣1035)
- 三、最大子序和(力扣53)
- 四、判断子序列(力扣392)
前言
1、最长公共子序列
2、不相交的线
3、最大子序和
4、判断子序列
一、最长公共子序列(力扣1143)
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

分析:
感觉类似于单词拆分问题
单词拆分问题
1、dp[i]数组以及下标含义
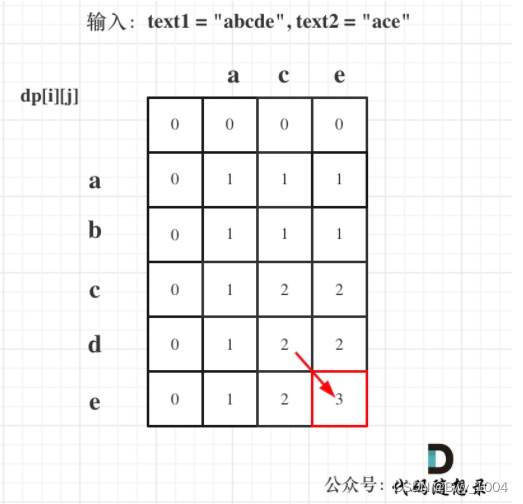
dp[i][j]: 以i-1为结尾的text1子数组和以j-1为结尾的text2子数组的最长公共子序列长度。
这样定义的好处可以节省初始化里面的过程
2、递推公式
if(nums1[i-1]==nums2[j-1])
dp[i][j] = dp[i-1][j-1]+1;
else dp[i][j] = max(dp[i-1][j], dp[i][j-1])
3、初始化
dp[0][j] = 0;
dp[i][0] = 0;
4、遍历顺序
先遍历哪个字符串都可以 从前向后
5、举例推导dp数组
以输入:text1 = “abcde”, text2 = “ace” 为例,dp状态如图:
class Solution {public int longestCommonSubsequence(String text1, String text2) {char[] char1 = text1.toCharArray();char[] char2 = text2.toCharArray();int[][] dp = new int[char1.length+1][char2.length+1];for(int i=1;i<=char1.length;i++){for(int j=1;j<=char2.length;j++){if(char1[i-1]==char2[j-1]){dp[i][j] = dp[i-1][j-1]+1;}else dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);}}return dp[char1.length][char2.length];}
}

二、不相交的线(力扣1035)
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足满足:
nums1[i] == nums2[j]
且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。

分析:
与上一题几乎一模一样
说是求绘制的最大连线数,其实就是求两个字符串的最长公共子序列的长度!
class Solution {public int maxUncrossedLines(int[] nums1, int[] nums2) {int[][] dp = new int[nums1.length+1][nums2.length+1];for(int i=1;i<=nums1.length;i++){for(int j=1;j<=nums2.length;j++){if(nums1[i-1]==nums2[j-1])dp[i][j] = dp[i-1][j-1]+1;else dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);}}return dp[nums1.length][nums2.length];}
}

三、最大子序和(力扣53)
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
分析:
之前用贪心算法已经求解过
贪心算法求解
通过动态规划求解:
1、确定dp数组以及下标的含义
dp[i]:包括下标i(以nums[i]为结尾)的最大连续子序列和为dp[i]。
2、递推公式
dp[i]只有两个方向可以推出来:
- dp[i - 1] + nums[i],即:nums[i]加入当前连续子序列和
- nums[i],即:从头开始计算当前连续子序列和
dp[i] = Math.max(dp[i-1]+nums[i],nums[i]);
3、初始化
dp[i]是依赖于dp[i - 1]的状态,dp[0]就是递推公式的基础。
dp[0] = nums[0]
4、遍历顺序
从前向后遍历
class Solution {public int maxSubArray(int[] nums) {int[] dp = new int[nums.length];dp[0] = nums[0];int res = dp[0];for(int i=1;i<nums.length;i++){dp[i] = Math.max(dp[i-1]+nums[i],nums[i]);res = Math.max(res,dp[i]);}return res;}
}

四、判断子序列(力扣392)
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)

暴力求解:
class Solution {public boolean isSubsequence(String s, String t) {int index = -1;for (char c : s.toCharArray()){index = t.indexOf(c, index+1);if (index == -1) return false;}return true;}
}
动态规划求解:
1、dp[]数组以及下标含义
dp[i][j] 表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。
2、递推公式
if(s[i-1]==t[j-1])
dp[i][j] = dp[i-1][j-1]+1
else
dp[i][j] = dp[i][j-1]
参考最长公共子序列(力扣1143)
3、初始化
dp[0][j] = 0;
dp[i][0] = 0;
4、遍历顺序
先遍历哪个字符串都可以 从前向后
class Solution {public boolean isSubsequence(String s, String t) {char[] ss = s.toCharArray();char[] tt = t.toCharArray();int[][] dp = new int[ss.length+1][tt.length+1];for(int i=1;i<=ss.length;i++){for(int j=1;j<=tt.length;j++){if(ss[i-1]==tt[j-1])dp[i][j] = dp[i-1][j-1]+1;elsedp[i][j] = dp[i][j-1];}} return dp[ss.length][tt.length]==ss.length;}
}

相关文章:

day49【代码随想录】动态规划之最长公共子序列、不相交的线、最大子序和、判断子序列
文章目录前言一、最长公共子序列(力扣1143)二、不相交的线(力扣1035)三、最大子序和(力扣53)四、判断子序列(力扣392)前言 1、最长公共子序列 2、不相交的线 3、最大子序和 4、判断…...
)
华为OD机试真题Python实现【字母消消乐】真题+解题思路+代码(20222023)
字母消消乐 题目 游戏规则: 输入一个只包含英文字母的字符串, 字符串中的两个字母如果相邻且相同,就可以消除。 在字符串上反复执行消除的动作, 直到无法继续消除为止,此时游戏结束。 输出最终得到的字符串长度。 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试…...

程序中的日期使用问题-格式转化:SimpleDateFormat、org.apache.commons.lang3.time.DateUtils
前言 日期使用问题主要是格式转换的问题 场景:通过excel导入数据,其中一个字段为出生日期,需要对字段值进行合法性校验 博客地址:芒果橙的个人博客 【http://mangocheng.com】 一、个人浅谈日期 时间日期作为一个基础的标识和维度…...

C++——map和set的应用总结
目录1. 关联式容器2. 键值对3. 树形结构的关联式容器3.1 set3.1.1 set的介绍3.1.2 set的使用3.2 multiset3.2.1 multiset的介绍3.2.2 multiset的使用3.3 map3.3.1 map的介绍3.3.2 map的使用operator[]3.4 multimap3.4.1 multimap的介绍3.4.2 multimap的使用3.5 map和set在OJ中的…...

学习Python可以做什么工作?
一: 1、web开发:Python拥有非常完善与web服务器交互的库,大量的免费网页模板,相对于更具有优势,同时还具有非常优秀的Django框架,功能齐全。目前国内的豆瓣网、果壳网等,国外的Google、YouTube等…...
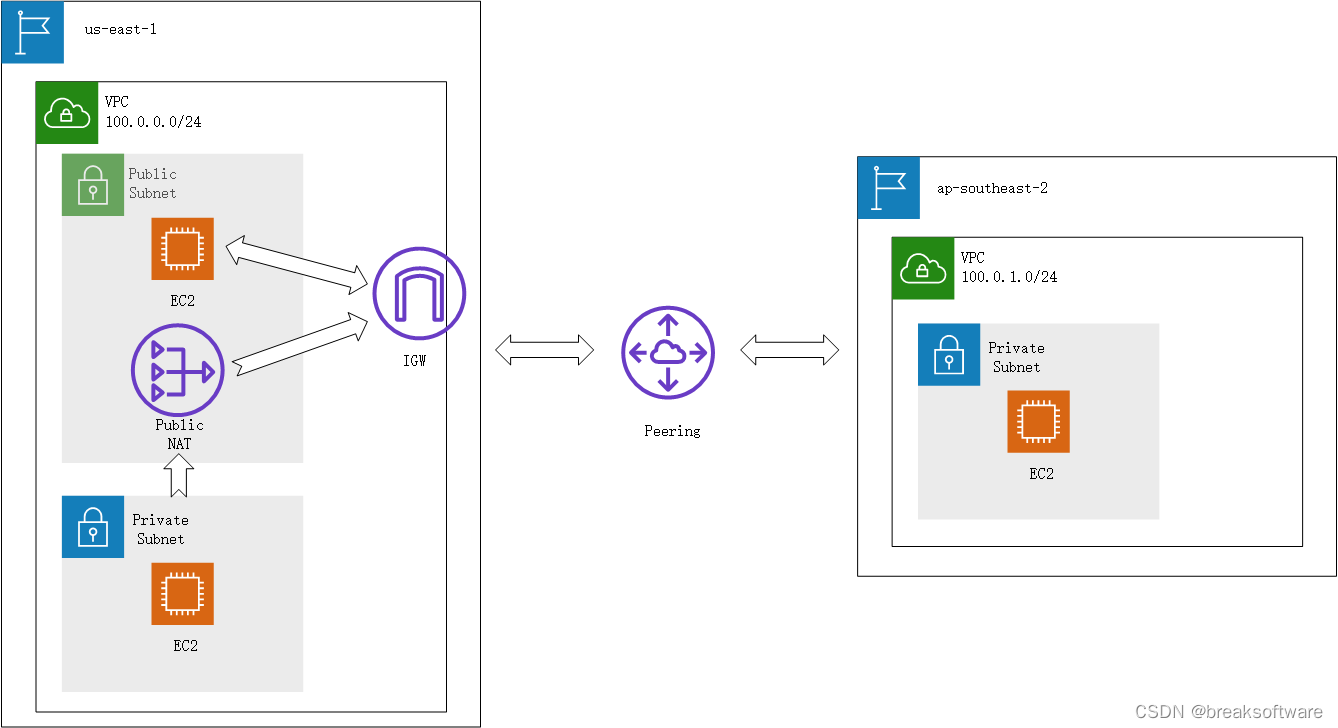
AWS攻略——Peering连接VPC
文章目录创建IP/CIDR不覆盖的VPC创建VPC创建子网创建密钥对创建EC2创建Peering接受Peering邀请修改各个VPC的路由表修改美东us-east-1 pulic subnet的路由修改悉尼ap-southeast-2路由测试知识点我们回顾下《AWS攻略——VPC初识》中的知识: 一个VPC只能设置在一个Re…...

程序员遇到人生低谷期怎么做?
每个人的一生都是起起伏伏的,你不会天天高潮,总会经历一段又一段的不如意,你怎么把握这一段段时间,如何掌控人生节奏,都源于对人生低谷期的回答。 尤其是2022年,程序员受到的冲击并不小,从年初…...

理解IM消息“可靠性”和“一致性”问题,以及解决方案探讨
试想如果一个IM连发出的消息都不知道对方到底能不能收到、发出的聊天内容对方看到的到底是不是“胡言乱语”(严重乱序问题),这样的APP用户肯定不会让他在手机上过夜(肯定第一时间卸载了),因为最基本的聊天逻…...

2021-08-29
服务器 主:172.17.0.2 master 备:172.17.0.3 slave1 lvs虚拟IP:172.17.0.100 #nginx下载地址 http://nginx.org/download/ 本地文件路径 1.dockerfile构建nginx FROM centos:7 ADD nginx-1.6.0.tar.gz /usr/local COPY nginx_install.sh /usr/local RUN sh …...

第八题、哈夫曼编码大全
题目: 哈夫曼编码大全 描述: 关于哈夫曼树的建立,编码,解码。 输入 第一行输入数字N,代表总共有多少个字符以及权值 第二第三行分别是一行字符串,以及每个字符对应的权值 接下来输入一个数M,表…...
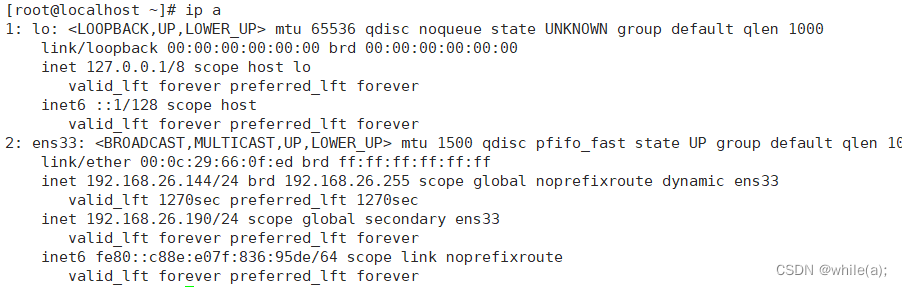
linux集群技术(二)--keepalived(高可用集群)(二)
案例1--keepalived案例2--keepalived Lvs集群1.案例1--keepalived 1.1 环境 初识keepalived,实现web服务器的高可用集群。 Server1: 192.168.26.144 Server2: 192.168.26.169 VIP: 192.168.26.190 1.2 server1 创建etc下的…...
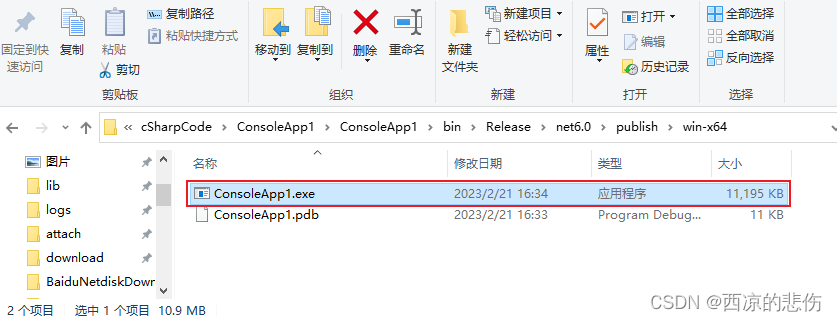
C# 控制台程序的开发和打包为一个exe文件
目录前言一、我的第一个C#控制台程序二、发布为一个exe文件前言 本文通过C#编写一个简单的示例计算器,来演示C#的使用和使用 Visual Studio 打包为一个 exe 文件。 一、我的第一个C#控制台程序 所谓控制台程序,就是没有界面,运行程序后只有…...
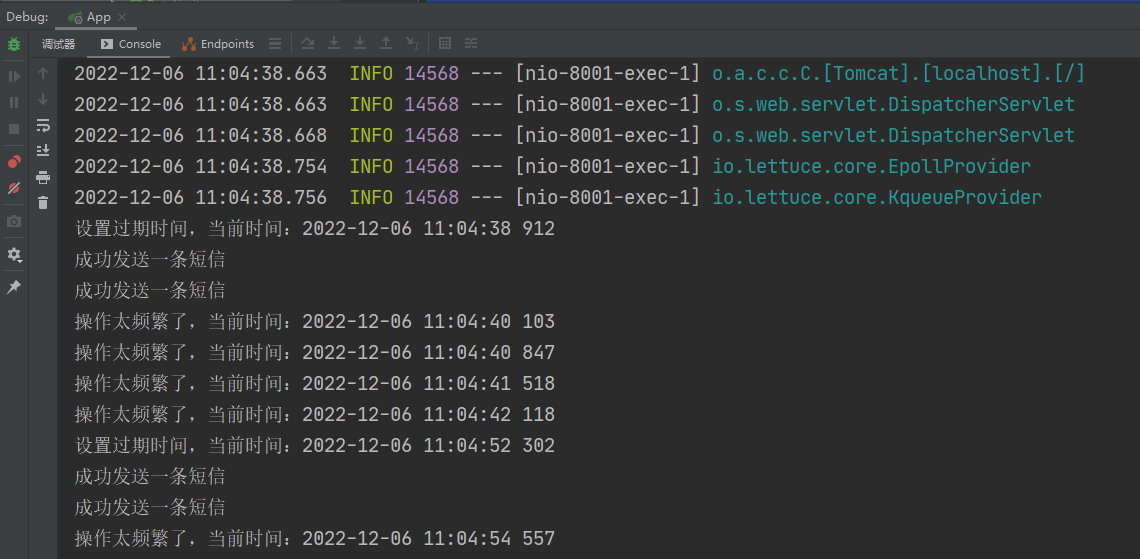
Redis实战案例
文章目录1、SpringBoot整合Redis1.1、新建项目1.2、接口编写1.3、集成Redis1.3、测试1.4、序列化问题2、Redis实现分布式缓存2.1、背景介绍2.2、代码编写2.3、缓存改造2.4、小结3、RedisAOP自定义注解,优雅实现分布式缓存3.1、自定义注解3.2、AOP切面类3.3、测试3.4…...

slice和splice区别
slice和splice区别 splice和slice是数组中的两个重要的方法。 slicesplice不会改变原数组改变原数组返回原数组中的部分元素返回原数组中被删除的元素组成的新数组用来选择数组中的元素用于在数组中插入或者删除元素 1.splice的语法 array.splice(index,howmany,item1,…,ite…...

动态规划从入门到精通-蓝桥杯
一、了解动态规划1.简单来说动态规划是一种状态转移与递推2.例题引入——最少硬币问题有多个不同面值的硬币(任意面值); 数量不限; 输入金额S,输出最少硬币组合。 (回顾用贪心求解硬币问题。)贪心法硬币面值1、2、5。支…...

Docker部署Prometheus
文章目录Prometheus相关介绍Docker部署Prometheus说明安装Prometheus搜索镜像拉取镜像配置启动容器进入容器遇到的问题Are you trying to mount a directory onto a file (or vice-versa)?其他可能的错误Prometheus相关介绍 官方介绍,非常的清楚: http…...

JavaScript的执行顺序
前言 在说 JavaScript 的执行顺序之前,我们先回答一下以下几组程序的输出结果 第 1 组 const output (v) > {console.log(v); };setTimeout(() > {console.log(1); }, 0); output(2); console.log(3);// 2 3 1第 2 组 new Promise((resolve) > {conso…...
C++11智能指针std::shared_ptr介绍及使用
介绍 shared_ptr是一种智能指针(smart pointer),作用有如同指针,但会记录有多少个shared_ptrs共同指向一个对象。这便是所谓的引用计数(reference counting),比如我们把只能指针赋值给另外一个对象,那么对象多了一个智能指针指向它,所以这个时候引用计数…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 数字的排列(Python) | 机试题+算法思路+考点+代码解析 【2023】
数字的排列 题目 小华是个很有对数字很敏感的小朋友, 他觉得数字的不同排列方式有特殊的美感。 某天,小华突发奇想,如果数字多行排列, 第一行1个数, 第二行2个, 第三行3个, 即第n行n个数字,并且奇数行正序排列, 偶数行逆序排列,数字依次累加。 这样排列的数字一定很…...
-常见面试题)
Android 事件分发机制(4)-常见面试题
目录 1.你了解过Android的事件分发机制吗?请大致介绍一下 2、如果父view中不拦截down事件,拦截move,up事件,在子view中设置了requestDisallowInterceptTouchEvent(true);(请求父view不拦截事件)这个标志后,…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...
