动态规划从入门到精通-蓝桥杯
一、了解动态规划
1.简单来说动态规划是一种状态转移与递推
2.例题引入——最少硬币问题
有多个不同面值的硬币(任意面值);
数量不限;
输入金额S,输出最少硬币组合。
(回顾用贪心求解硬币问题。)贪心法
硬币面值1、2、5。支付13元,要求硬币数量最少。
贪心法:
(1) 5元硬币,2个
(2) 2元硬币,1个
(3) 1元硬币,1个
正确! 答案是:2枚5元硬币+1枚2元硬币+1枚1元硬币。
硬币面值1、2、4、5、6。支付9元,要求硬币数量最少。
贪心法:
(1) 6元硬币,1个
(2) 2元硬币,1个
(3) 1元硬币,1个
错误! 答案是:1枚5元硬币+1枚4元硬币。
======>硬币问题的正解是动态规划!
动态规划
给定1,5,10,25,50这5种面值的硬币;
数量不限;
输入金额S,输出最少硬币组合。首先定义数组Min[ ] 记录最少硬币数量。
对输入的某个金额i,Min[i]是最少的硬币数量。
1. 只考虑1元面值的硬币。

i=1元时,等价于:i=i-1 = 0元需要的硬币数量,加上1个1元硬币。
------>其中把Min[ ]叫做“状态”;把Min[ ]的变化叫做“状态转移”。
2.所有金额仍然都只用1元硬币。

i=2元时,等价于:i=i-1 = 1元需要的硬币数量,加上1个1元硬币。
i=3元时,...
i=4元时,...
3.在1元硬币的计算结果基础上,再考虑加上5元硬币的情况。从i=5开始就行了。

i=5元时,等价于:
(1) i = i-5 = 0元需要的硬币数量,加上1个5元硬币。Min[5]=1
(2) 原来的Min[5]=5。
取 (1) (2)的最小值,所以Min[5]=1。
i=6元时,等价于:
(1) i = i-5 = 1元需要的硬币数量,加上1个5元硬币。Min[6]=2
(2) 原来的Min[6]=6。
取 (1) (2)的最小值,所以Min[6]=2。
i=7元时,...
i=8元时,...
动态规划总结
用1元和5元硬币,结果:

递推关系(状态转移方程):
Min[i] = min(Min[i], Min[i - 5] + 1)
继续处理其它面值硬币。
动态规划实现代码(实现递推关系)

上面代码状态名是Min[ ],但是其实习惯上把状态命名为dp[ ]更好。
二、动态规划的两个特征
1.重叠子问题
子问题是原大问题的小版本,计算步骤完全一样;计算大问题的时候,需要多次重复计算小问题。
一个子问题的多次计算,耗费了大量时间。用DP处理重叠子问题,每个子问题只需要计算一次,从而避免了重复计算,这就是DP效率高的原因。
2.最优子结构
首先,大问题的最优解包含小问题的最优解。
其次,可以通过小问题的最优解推导出大问题的最优解。
三、记忆化
如果各个子问题不是独立的,如果能够保存已经解决的子问题的答案,在需要的时候再找出已求得的答案,可以避免大量的重复计算。
基本思路:用一个表记录所有已解决的子问题的答案,不管该问题以后是否被用到,只要它被计算过,就将其结果填入表中。
四、动态规划求解过程图解
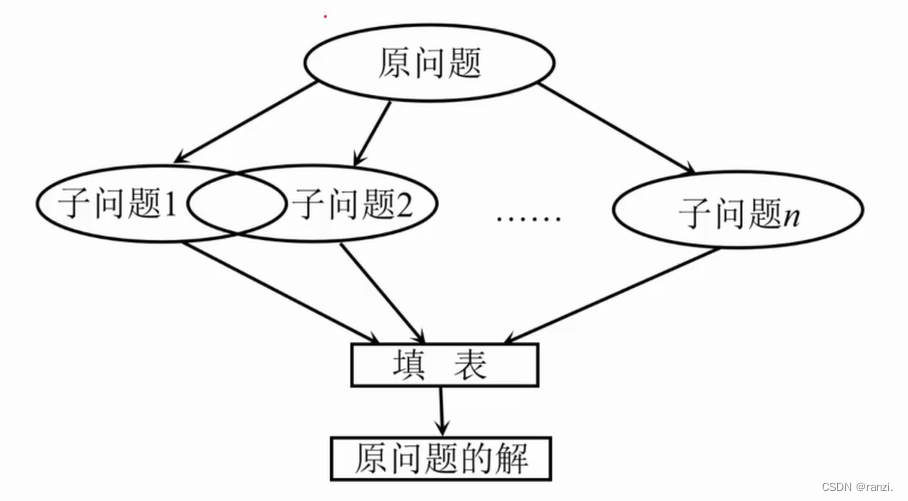
五、最经典的动态规划问题——0/1背包
给定n种物品和一个背包:
物品i的重量是wi,
其价值为Vi,
背包的容量为C。背包问题:
选择装入背包的物品,使得装入背包中物品的总价值最大。
如果在选择装入背包的物品时,对每种物品i只有两种选择:
装入背包或不装入背包,称为0/1背包问题。设xi表示物品i装入背包的情况:
xi=0,表示物品i没有被装入背包x;
i=1,表示物品i被装入背包。
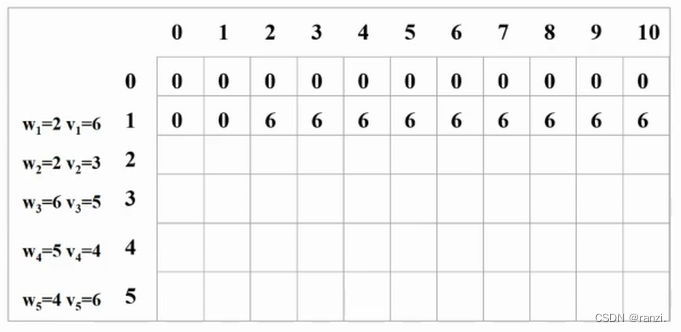
有5个物品,重量分别是{2,2,6,5,4},
价值分别为{6,3,5,4,6},
背包的容量为10。定义一个(n+1)X(C+1)的二维表dp[ ][ ]。
dp[i][i]表示把前i个物品装入容量为j的背包中获得的最大价值。
填表:按只放第1个物品、只放前2个、只放前3个......一直到放完,这样的顺序考虑。(从小问题扩展到大问题)
1、只装第1个物品。(横向是递增的背包容量)
2、只装前2个物品。
如果第2个物品重量比背包容量大,那么不能装第2个物品,情况和只装第1个一样。
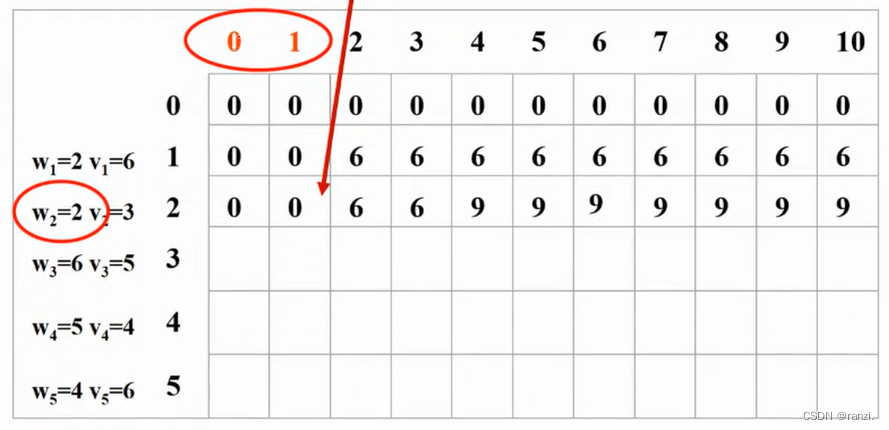
如果第2个物品重量小于等于背包容量,那么:
(1)如果把物品2装进去(重量是2),那么相当于只把1装到(容量-2)的背包中。
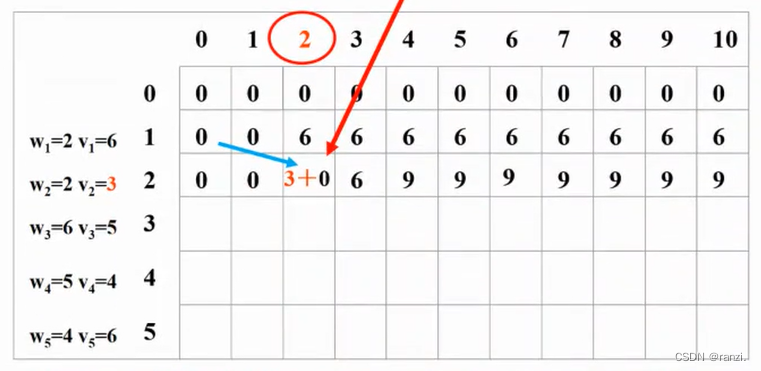
需要用到前面的需要用到前面的结果,即已经解决的子问题的答案经解决的子问题的答案。
(2)如果不装2,那么相当于只把1装到背包中。
------>取(1) 和 (2)的最大值。

3、只装前3个物品。
如果第3个物品重量比背包容量大,那么不能装第3个物品,情况和只装第1、2个一样。
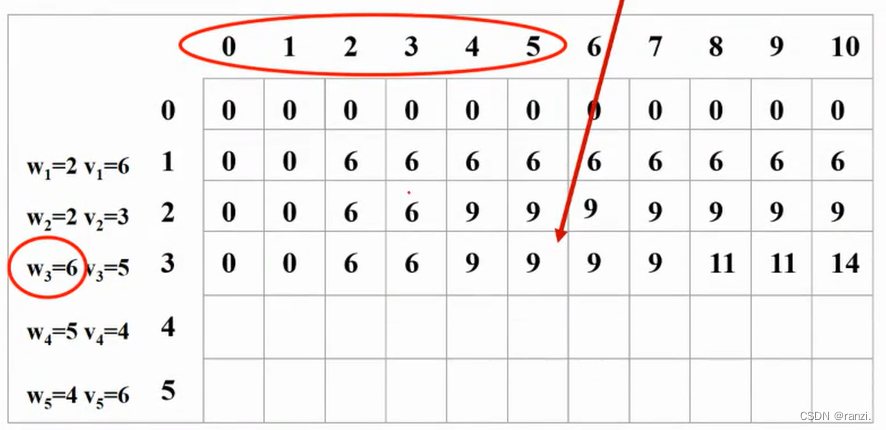
如果第3个物品重量小于等于背包容量,那么:
(1)如果把物品3装进去(重量是6),那么相当于只把1、2装到(容量-6)的背包中。

(2)如果不装3,那么相当于只把1、2装到背包中。
------>取(1) 和 (2)的最大值。
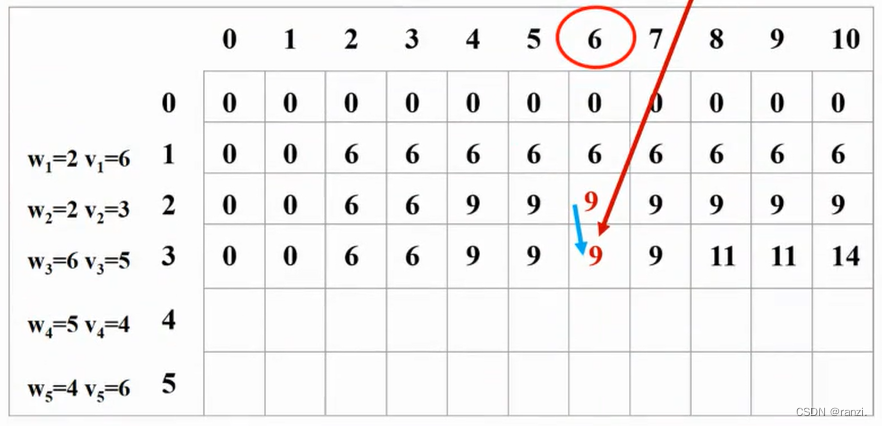
按这样的规律一行行填表,直到结束。现在回头考虑,装了哪些物品。
看最后一列,15>14,说明装了物品5,否则价值不会变化。

六、蓝桥杯真题(1174号)


1.DP状态设计
DP状态: 定义二维数组dp[ ][ ],大小为N * C。
dp[i][j]:把前i个物品(从第1个到第i个) 装入容量为j的背包中获得的最大价值。
把每个dp[i][j]看成一个背包: 背包容量为j,装1~i这些物品。最后得到的dp[N][C]就是问题的答案:把N个物品装进容量C的背包的最大价值。
2.DP状态转移方程(递推公式)
递推计算到dp[i][j],分2种情况:
(1)第i个物品的体积比容量j还大,不能装进容量的背包。那么直接继承前i-1个物品装进容量j的背包的情况即可: dp[i][j] = dp[i-1][j]。
(1)第i个物品的体积比容量j小,能装进背包。又可以分为2种情况: 装或者不装第i个。
1)装第i个。从前i-1个物品的情况下推广而来,前i-1个物品是dp[i-1][j]。第i个物品装进背包后,背包容量减少c[i],价值增加w[i]。有:
dp[i][j] = dp[i-1][j-c[i]] + w[i]。
2)不装第i个。那么:dp[i][j] = dp[i-1][j]。
取1)和2)的最大值,状态转移方程:
dp[i][j] = max(dp[i- 1][j],d[i- 1][j- c[i]] + w[i])
3.代码

七、空间优化:滚动数组
把dp[ ][ ]优化成一维的dp[ ],以节省空间。
Dp[i][]是从上面一行dp[i-1]算出来的,第i行只跟第i-1行有关系,跟更前面的行没有关系:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - c[i]] + w[i])
优化:只需要两行dp[0][]、dp[1][],用新的一行覆盖原来的一行,交替滚动。
经过优化,空间复杂度从O(N*C)减少为O(C)
1.交替滚动
定义:dp[2][i]: 用dp[O][]和dp[1][]交替滚动。
优点:逻辑清晰、编码不易出错,建议初学者采用这个方法。
代码:
now始终指向正在计算的最新的一行,old指向已计算过的旧的一行。
对照原递推代码,now相当于i,old相当于i - 1。

对照:
未经优化

优化之后

2.自我滚动
继续精简:用一个一维的dp[ ]就够了,自己滚动自己。
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - c[i]] + w[i])

对照:
未经优化

优化之后
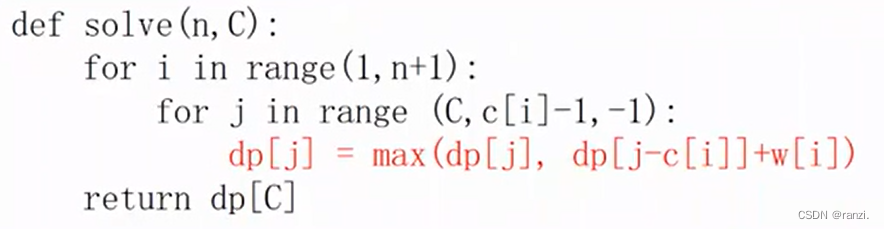
注意:自我滚动时j从小往大循环是错误的
优化之前填表的过程

自我滚动填表的过程

例如i = 2时,左图的dp[5]经计算得到dp[5] = 9,把dp[5]更新为9。
右图中继续往后计算,当计算dp[8]时,得dp[8] = dp[5]’ + 3 = 9+3 = 12。
这个答案是错的。
错误的产生是滚动数组重复使用同一个空间引起的。
注意:自我滚动时j从大往小循环是正确的
优化之前填表的过程

自我滚动填表的过程

例如i = 2时,首先计算最后的dp[9] = 9,它不影响前面状态的计算。
相关文章:

动态规划从入门到精通-蓝桥杯
一、了解动态规划1.简单来说动态规划是一种状态转移与递推2.例题引入——最少硬币问题有多个不同面值的硬币(任意面值); 数量不限; 输入金额S,输出最少硬币组合。 (回顾用贪心求解硬币问题。)贪心法硬币面值1、2、5。支…...

Docker部署Prometheus
文章目录Prometheus相关介绍Docker部署Prometheus说明安装Prometheus搜索镜像拉取镜像配置启动容器进入容器遇到的问题Are you trying to mount a directory onto a file (or vice-versa)?其他可能的错误Prometheus相关介绍 官方介绍,非常的清楚: http…...

JavaScript的执行顺序
前言 在说 JavaScript 的执行顺序之前,我们先回答一下以下几组程序的输出结果 第 1 组 const output (v) > {console.log(v); };setTimeout(() > {console.log(1); }, 0); output(2); console.log(3);// 2 3 1第 2 组 new Promise((resolve) > {conso…...
C++11智能指针std::shared_ptr介绍及使用
介绍 shared_ptr是一种智能指针(smart pointer),作用有如同指针,但会记录有多少个shared_ptrs共同指向一个对象。这便是所谓的引用计数(reference counting),比如我们把只能指针赋值给另外一个对象,那么对象多了一个智能指针指向它,所以这个时候引用计数…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 数字的排列(Python) | 机试题+算法思路+考点+代码解析 【2023】
数字的排列 题目 小华是个很有对数字很敏感的小朋友, 他觉得数字的不同排列方式有特殊的美感。 某天,小华突发奇想,如果数字多行排列, 第一行1个数, 第二行2个, 第三行3个, 即第n行n个数字,并且奇数行正序排列, 偶数行逆序排列,数字依次累加。 这样排列的数字一定很…...
-常见面试题)
Android 事件分发机制(4)-常见面试题
目录 1.你了解过Android的事件分发机制吗?请大致介绍一下 2、如果父view中不拦截down事件,拦截move,up事件,在子view中设置了requestDisallowInterceptTouchEvent(true);(请求父view不拦截事件)这个标志后,…...

计算机四级 [操作系统] | 选择题 2 重点标注版
1.某一个单道批处理系统几乎同时依次到达4个作业,这4个作业的预计运行时间分别为8、4、4和4分钟,按照短作业优先的调度算法运行,请问该批作业的平均周转时间为多少 B A. 14分钟 B. 11分钟 C. 20分钟 D. 10分钟 2.下列与进程具有一一对应的关…...

想玩好ChatGPT?不妨看看这篇文章
相信点进来的铁汁,此时已经对 ChatGPT 有所了解,并想上手体验一番 首先大伙儿要注意,不要被骗了。 现在很多商家提供的 ChatGPT 服务,不仅价格奇高,而且据我所知,有些压根不是 ChatGPT 。 想玩最好去官网注册,具体方法大伙自个儿查一查嗷。 怎么用好 ChatGPT 虽然 …...
day31 IO流
文章目录回顾collectionArrayTestListHashSetTsetHashMapTestPropertiesTreeSetTestIO流FileInputStreamTest01 文件流初步FileInputStreamTest02 循环读FileStreamTest03FileInputStreamTes04 需要掌握FiLeInputStreamTest5FileOutputStreamTest01Copy1 文件拷贝FileReaderTes…...

Linux 防火墙配置(iptables和firewalld)
目录 防火墙基本概念 Iptables讲解 Iptables表 Iptables规则链 Iptables控制类型 Iptables命令配置 firewalld讲解 Firewalld区域概念 Firewalld两种配置方法 firewall-cmd命令行基础配置 firewall-config图形化配置 防火墙基本概念 防火墙就是根据系统管理员设定的…...
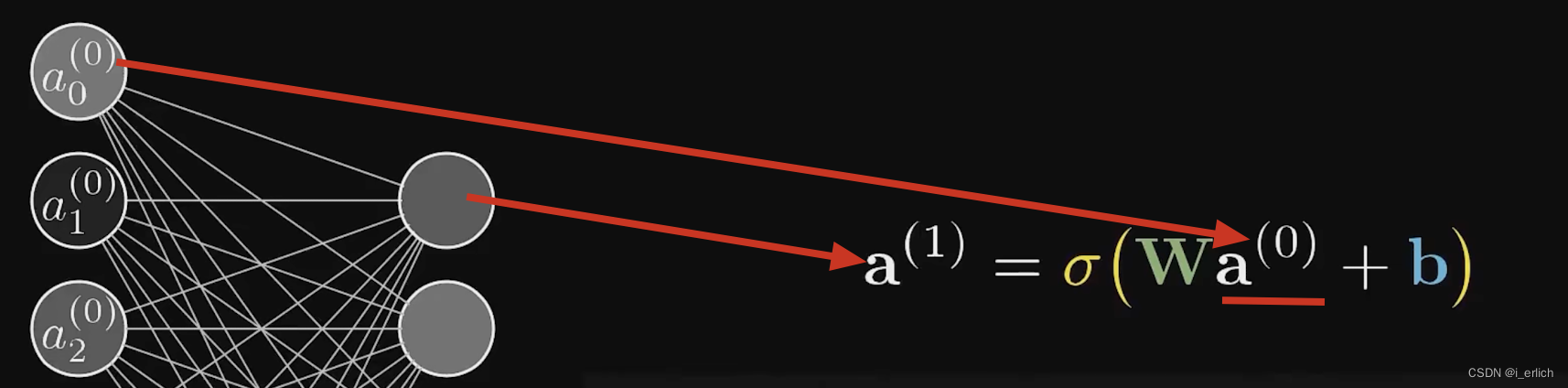
深度学习基础(一)
记得17年第一次阅读深度学习相关文献及代码觉得不是很顺畅,做客户端开发时间久了,思维惯性往往觉得比较迷茫。 而且文章中涉及的数学公式及各种符号又觉得很迷惑,虽然文章读下来了,代码也调试过了,意识里并没有轻松的…...

Maven 常用命令
mvn archetype: create :创建Maven 项目mvn compile :编译源代码。mvn deploy:发布项目。mvn test-compile :编译测试源代码mvn test:运行应用程序中的单元测试mvn site:生成项目相关信息的网站mvn clean:清除项目目录中的生成结果mvn package:根据项目生成的iar/war等mvn inst…...

2023年100道最新Android面试题,常见面试题及答案汇总
除了需要掌握牢固的专业技术之外,还需要刷更多的面试去在众多的面试者中杀出重围。小编特意整理了100道Android面试题,送给大家,希望大家都能顺利通过面试,拿下高薪。赶紧拿去吧~~文末有答案Q1.组件化和arouter原理Q2.自定义view&…...
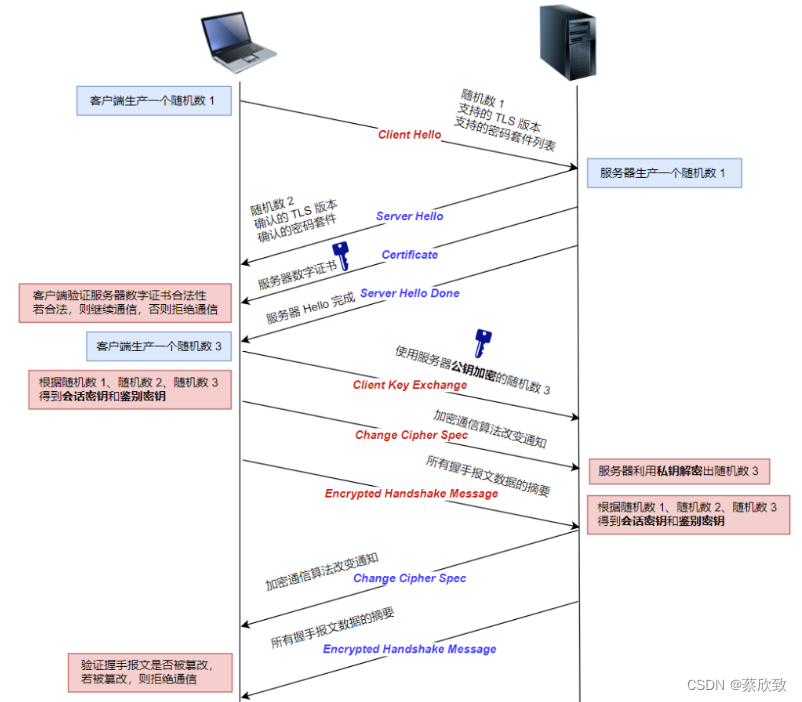
[JavaEE系列] 详解面试中HTTP协议HTTPS协议
文章目录HTTP不安全HTTPS中的加密算法对称加密非对称加密混合加密HTTPS中的摘要算法HTTPS中的数字证书SSL /TLS握手TCP建立连接(三次握手)三次握手中常见的面试题:TCP断开连接(四次挥手)四次挥手中常见的面试题&#x…...
mac 好用的类似Xshell工具
下载royal TSX 5.1.1 http://share.uleshi.com/f/9490615-685692355-33bf1e修改mac的etc/hosts文件权限访达(鼠标右键) -> 前往文件夹 ->输入/private --> 打开etc/hosts --> 显示简洁(鼠标右键) --> 权限改成读和写hosts文件写入如下内容:# Royal T…...

浅谈SQL中的union和union all
文章目录概念基础语法使用技巧区别总结概念 MySQL UNION 操作符用于连接两个以上的 SELECT 语句的结果组合到一个结果集合中。多个 SELECT 语句会删除重复的数据。 UNION 操作符选取不同的值,如果允许得到重复的值,可以使用 UNION ALL 基础语法 -- u…...

P6软件应用的核心收益
卷首语 提供了多用户、多项目的功能模块,支持多层次项目等级划分,资源分配计划,记录实际数据,自定义视图,并具有用户定义字段的扩展功能。 利用最佳实践,建立企业模板库 P6软件支持用户使用模板编制项目…...
性能测试中,我遇到的8个常见问题总结
性能压测中我们需要明白以下几点: 1、好的开始是成功的一半,前期的准备非常重要; 2、过程中,关注每个细节,多个维度监控; 3、在调优中多积累经验; 4、对结果负责,测试报告要清晰…...
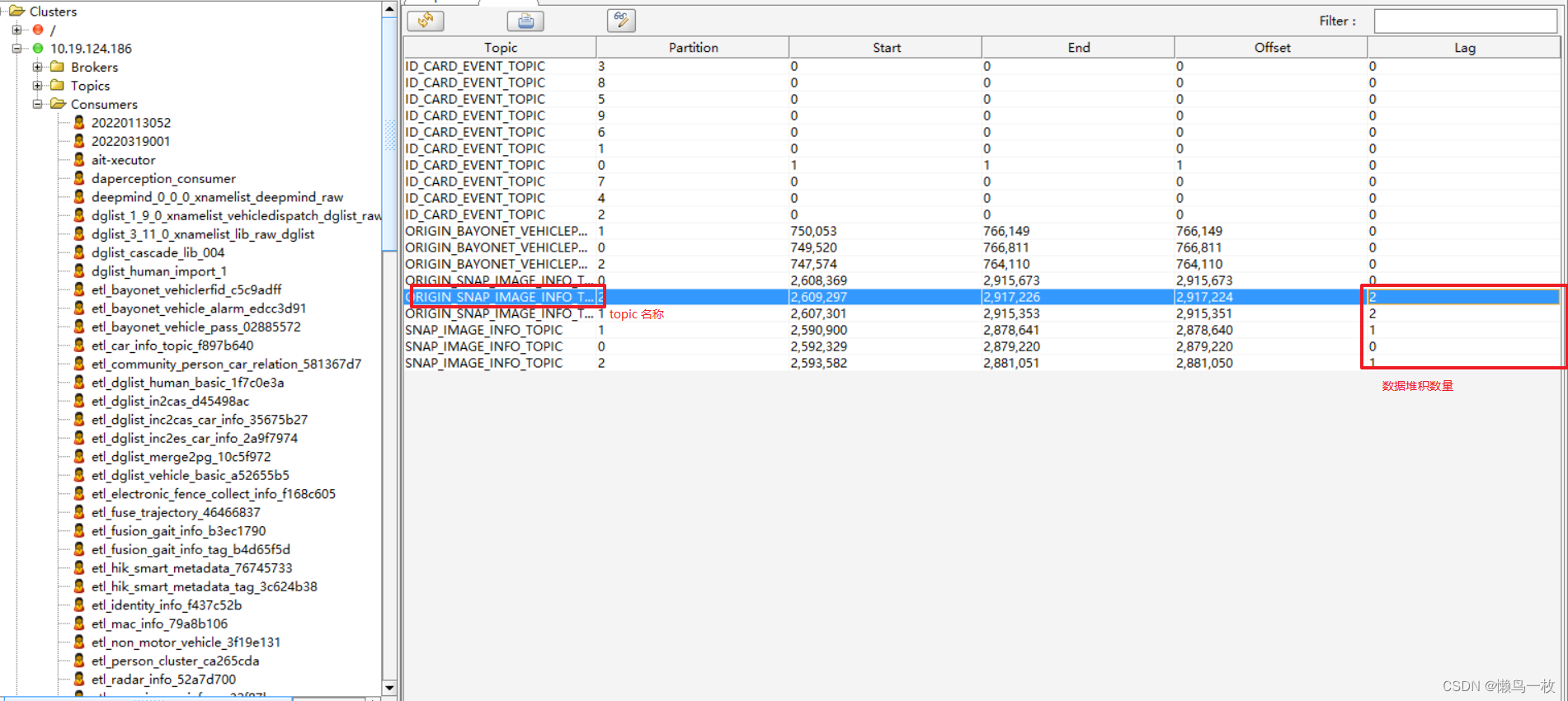
kafka架构体系
Kafka简介 Kafka是一个由Scala和Java编写的企业级的消息发布和订阅系统,最早是由Linkedin公司开发,最终开源到Apache软件基金会的项目。Kafka是一个分布式的,支持分区的,多副本的和多订阅者的高吞吐量的消息系统,被广…...
【Kafka】三.Kafka怎么保证高可用 学习总结
Kafka 的副本机制 Kafka 的高可用实现主要依赖副本机制。 Broker 和 Partition 的关系 在分析副本机制之前,先来看一下 Broker 和 Partition 之间的关系。Broker 在英文中是代理、经纪人的意思,对应到 Kafka 集群中,是一个 Kafka 服务器节…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...
