学习Python可以做什么工作?
一:
1、web开发:Python拥有非常完善与web服务器交互的库,大量的免费网页模板,相对于更具有优势,同时还具有非常优秀的Django框架,功能齐全。目前国内的豆瓣网、果壳网等,国外的Google、YouTube等都采用Python作为部分功能的开发。
2、系统运维:在运维的工作中,有大量重复性工作的地方,并需要做管理系统、监控系统、发布系统等。在很早之前都是通过shell脚本来进行自动化操作,但是shell编程能力比较弱,可以实现的功能库很少,Python作为胶水语言,可以进行集成,对各类工具可以进行二次开发。
3、游戏开发:Python有很好的3D渲染库和游戏开发框架,有很多使用Python开发的游戏,如迪斯尼卡通城、黑暗之刃。由于Python脚本化的优点所在,类似于游戏剧本,在逻辑上更加灵活一些,修改起来也是非常方便的。其中pygame是非常出名的。
4、爬虫工作:在进行爬虫方面工作的时候,Python可谓是独占优势,Python拥有非常丰富的库,可以访问文档的接口,还可以进行更好的后期快速处理。
5、桌面软件:在Windows系统桌面开发领域上,Python可以做到无缝对接c++,支持支持Qt和GTK。
6、数据分析:Python被广泛地运用于科学和数字计算中,例如生物信息学、物理、建筑、地理信息系统、图像可视化分析、生命科学等,常用numpy、SciPy、Biopython、SunPy等。
7、人工智能:Python人工智能的首选语言,使用python是因为CPython和底层原因的融合使得开发起来更加方便。
1、人工智能
二:Python是人工智能的黄金语言,选择人工智能作为就业方向是理所当然的。
2、大数据
Python在大数据上比Java更加有效率,大数据虽然难学,但是Python可以更好地和大数据对接,尤其是大数据分析这个方向。
3、网络爬虫工程师
网络爬虫是数据采集的利器,利用Python可以更快的提升对数据抓取的精准程度和速度。
4、Python web全栈工程师
全栈工程师是指掌握多种技能,并能利用多种技能独立完成产品的人,也叫全端工程师(同时具备前端和后台能力)。
5、Python自动化运维
运维工作者对Python的需求也很大。
6、Python自动化测试
Python十分高效,目前做自动化测试的大部分的工作者都需要学习Python帮助提高测试效率。用Python测试也可以说是测试人员必备的工具了。
7、数据科学
Python有很多数据包是专门用来做数据科学,不过数据科学语言的知识背景也挺宽的,从统计学到计算机理论每一个分支都需要不断学习才可以做到与时俱进。
相关文章:

学习Python可以做什么工作?
一: 1、web开发:Python拥有非常完善与web服务器交互的库,大量的免费网页模板,相对于更具有优势,同时还具有非常优秀的Django框架,功能齐全。目前国内的豆瓣网、果壳网等,国外的Google、YouTube等…...
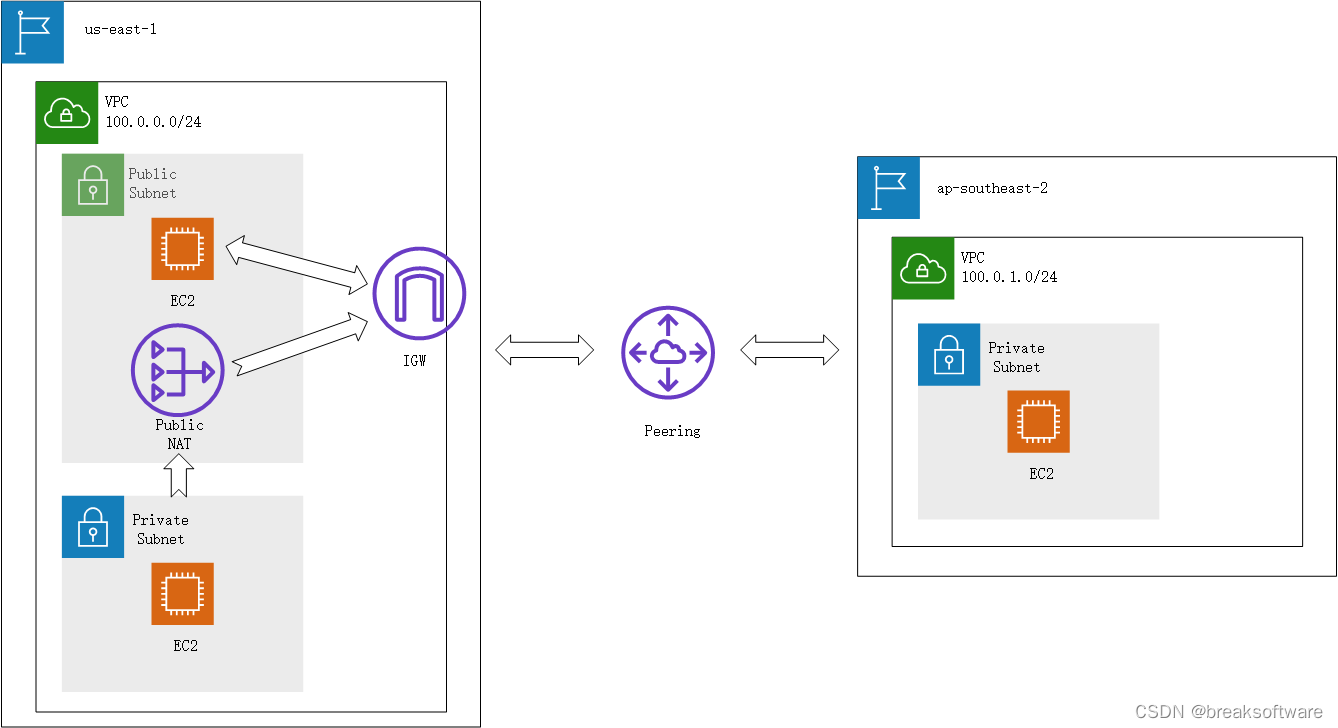
AWS攻略——Peering连接VPC
文章目录创建IP/CIDR不覆盖的VPC创建VPC创建子网创建密钥对创建EC2创建Peering接受Peering邀请修改各个VPC的路由表修改美东us-east-1 pulic subnet的路由修改悉尼ap-southeast-2路由测试知识点我们回顾下《AWS攻略——VPC初识》中的知识: 一个VPC只能设置在一个Re…...

程序员遇到人生低谷期怎么做?
每个人的一生都是起起伏伏的,你不会天天高潮,总会经历一段又一段的不如意,你怎么把握这一段段时间,如何掌控人生节奏,都源于对人生低谷期的回答。 尤其是2022年,程序员受到的冲击并不小,从年初…...

理解IM消息“可靠性”和“一致性”问题,以及解决方案探讨
试想如果一个IM连发出的消息都不知道对方到底能不能收到、发出的聊天内容对方看到的到底是不是“胡言乱语”(严重乱序问题),这样的APP用户肯定不会让他在手机上过夜(肯定第一时间卸载了),因为最基本的聊天逻…...

2021-08-29
服务器 主:172.17.0.2 master 备:172.17.0.3 slave1 lvs虚拟IP:172.17.0.100 #nginx下载地址 http://nginx.org/download/ 本地文件路径 1.dockerfile构建nginx FROM centos:7 ADD nginx-1.6.0.tar.gz /usr/local COPY nginx_install.sh /usr/local RUN sh …...

第八题、哈夫曼编码大全
题目: 哈夫曼编码大全 描述: 关于哈夫曼树的建立,编码,解码。 输入 第一行输入数字N,代表总共有多少个字符以及权值 第二第三行分别是一行字符串,以及每个字符对应的权值 接下来输入一个数M,表…...
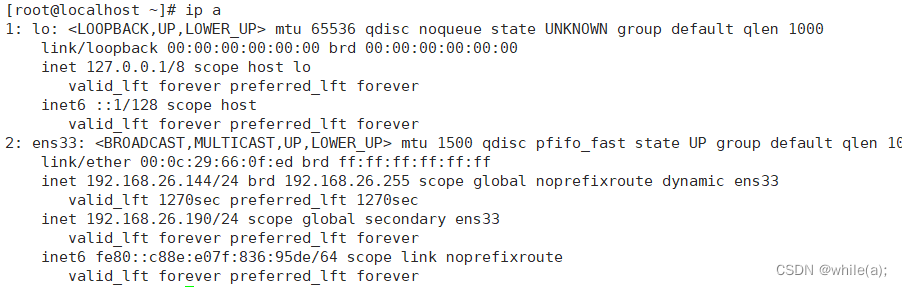
linux集群技术(二)--keepalived(高可用集群)(二)
案例1--keepalived案例2--keepalived Lvs集群1.案例1--keepalived 1.1 环境 初识keepalived,实现web服务器的高可用集群。 Server1: 192.168.26.144 Server2: 192.168.26.169 VIP: 192.168.26.190 1.2 server1 创建etc下的…...
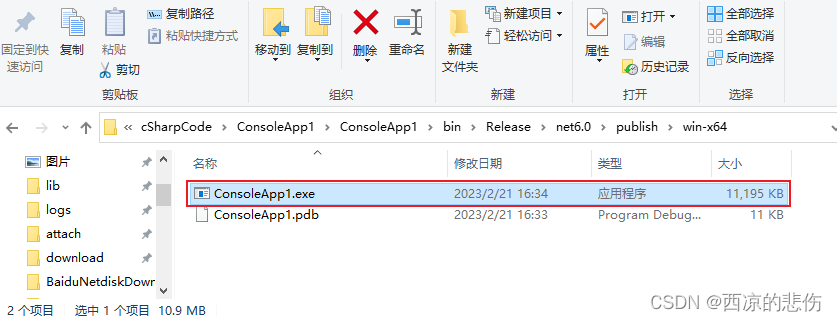
C# 控制台程序的开发和打包为一个exe文件
目录前言一、我的第一个C#控制台程序二、发布为一个exe文件前言 本文通过C#编写一个简单的示例计算器,来演示C#的使用和使用 Visual Studio 打包为一个 exe 文件。 一、我的第一个C#控制台程序 所谓控制台程序,就是没有界面,运行程序后只有…...
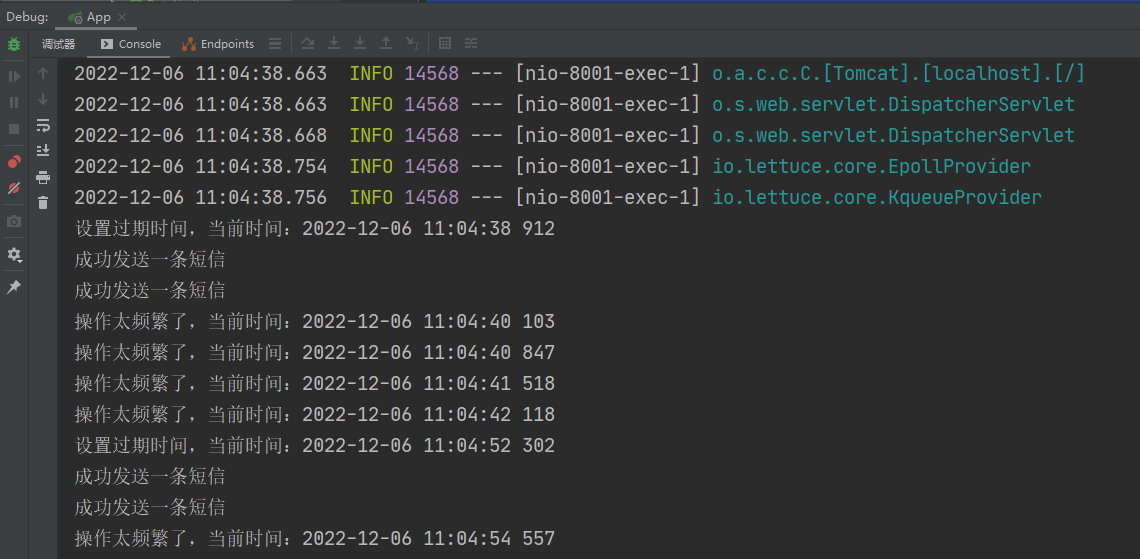
Redis实战案例
文章目录1、SpringBoot整合Redis1.1、新建项目1.2、接口编写1.3、集成Redis1.3、测试1.4、序列化问题2、Redis实现分布式缓存2.1、背景介绍2.2、代码编写2.3、缓存改造2.4、小结3、RedisAOP自定义注解,优雅实现分布式缓存3.1、自定义注解3.2、AOP切面类3.3、测试3.4…...

slice和splice区别
slice和splice区别 splice和slice是数组中的两个重要的方法。 slicesplice不会改变原数组改变原数组返回原数组中的部分元素返回原数组中被删除的元素组成的新数组用来选择数组中的元素用于在数组中插入或者删除元素 1.splice的语法 array.splice(index,howmany,item1,…,ite…...

动态规划从入门到精通-蓝桥杯
一、了解动态规划1.简单来说动态规划是一种状态转移与递推2.例题引入——最少硬币问题有多个不同面值的硬币(任意面值); 数量不限; 输入金额S,输出最少硬币组合。 (回顾用贪心求解硬币问题。)贪心法硬币面值1、2、5。支…...

Docker部署Prometheus
文章目录Prometheus相关介绍Docker部署Prometheus说明安装Prometheus搜索镜像拉取镜像配置启动容器进入容器遇到的问题Are you trying to mount a directory onto a file (or vice-versa)?其他可能的错误Prometheus相关介绍 官方介绍,非常的清楚: http…...

JavaScript的执行顺序
前言 在说 JavaScript 的执行顺序之前,我们先回答一下以下几组程序的输出结果 第 1 组 const output (v) > {console.log(v); };setTimeout(() > {console.log(1); }, 0); output(2); console.log(3);// 2 3 1第 2 组 new Promise((resolve) > {conso…...
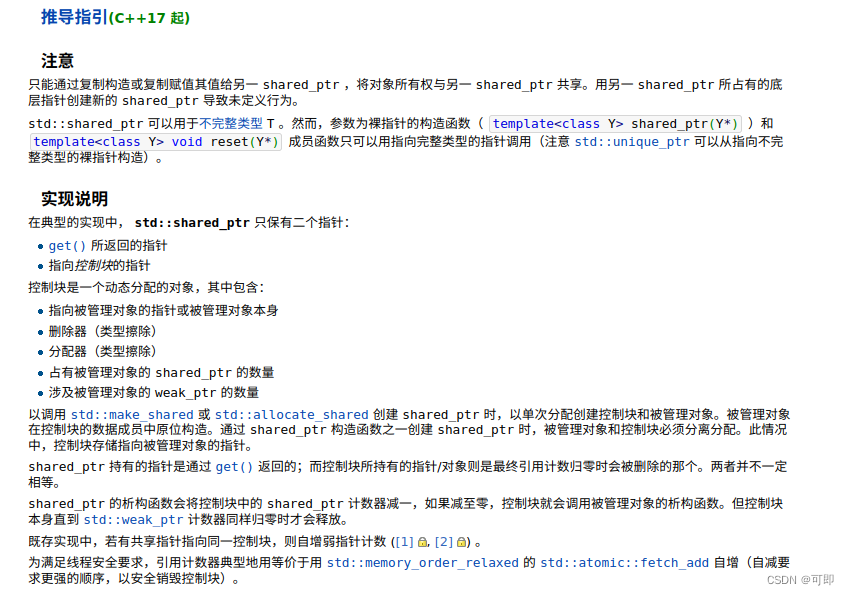
C++11智能指针std::shared_ptr介绍及使用
介绍 shared_ptr是一种智能指针(smart pointer),作用有如同指针,但会记录有多少个shared_ptrs共同指向一个对象。这便是所谓的引用计数(reference counting),比如我们把只能指针赋值给另外一个对象,那么对象多了一个智能指针指向它,所以这个时候引用计数…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 数字的排列(Python) | 机试题+算法思路+考点+代码解析 【2023】
数字的排列 题目 小华是个很有对数字很敏感的小朋友, 他觉得数字的不同排列方式有特殊的美感。 某天,小华突发奇想,如果数字多行排列, 第一行1个数, 第二行2个, 第三行3个, 即第n行n个数字,并且奇数行正序排列, 偶数行逆序排列,数字依次累加。 这样排列的数字一定很…...
-常见面试题)
Android 事件分发机制(4)-常见面试题
目录 1.你了解过Android的事件分发机制吗?请大致介绍一下 2、如果父view中不拦截down事件,拦截move,up事件,在子view中设置了requestDisallowInterceptTouchEvent(true);(请求父view不拦截事件)这个标志后,…...

计算机四级 [操作系统] | 选择题 2 重点标注版
1.某一个单道批处理系统几乎同时依次到达4个作业,这4个作业的预计运行时间分别为8、4、4和4分钟,按照短作业优先的调度算法运行,请问该批作业的平均周转时间为多少 B A. 14分钟 B. 11分钟 C. 20分钟 D. 10分钟 2.下列与进程具有一一对应的关…...

想玩好ChatGPT?不妨看看这篇文章
相信点进来的铁汁,此时已经对 ChatGPT 有所了解,并想上手体验一番 首先大伙儿要注意,不要被骗了。 现在很多商家提供的 ChatGPT 服务,不仅价格奇高,而且据我所知,有些压根不是 ChatGPT 。 想玩最好去官网注册,具体方法大伙自个儿查一查嗷。 怎么用好 ChatGPT 虽然 …...
day31 IO流
文章目录回顾collectionArrayTestListHashSetTsetHashMapTestPropertiesTreeSetTestIO流FileInputStreamTest01 文件流初步FileInputStreamTest02 循环读FileStreamTest03FileInputStreamTes04 需要掌握FiLeInputStreamTest5FileOutputStreamTest01Copy1 文件拷贝FileReaderTes…...

Linux 防火墙配置(iptables和firewalld)
目录 防火墙基本概念 Iptables讲解 Iptables表 Iptables规则链 Iptables控制类型 Iptables命令配置 firewalld讲解 Firewalld区域概念 Firewalld两种配置方法 firewall-cmd命令行基础配置 firewall-config图形化配置 防火墙基本概念 防火墙就是根据系统管理员设定的…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...
