【LeetCode算法系列题解】第36~40题
CONTENTS
- LeetCode 36. 有效的数独(中等)
- LeetCode 37. 解数独(困难)
- LeetCode 38. 外观数列(中等)
- LeetCode 39. 组合总和(中等)
- LeetCode 40. 组合总和 II(中等)
LeetCode 36. 有效的数独(中等)
【题目描述】
请你判断一个 9 x 9 的数独是否有效。只需要根据以下规则,验证已经填入的数字是否有效即可。
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次(请参考示例图)。
注意:
- 一个有效的数独(部分已被填充)不一定是可解的。
- 只需要根据以上规则,验证已经填入的数字是否有效即可。
- 空白格用
'.'表示。
【示例1】

输入:board =
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出:true
【示例2】
输入:board =
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出:false
解释:除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
【提示】
b o a r d . l e n g t h = = 9 board.length == 9 board.length==9
b o a r d [ i ] . l e n g t h = = 9 board[i].length == 9 board[i].length==9
board[i][j] 是一位数字(1-9)或者 '.'
【分析】
直接按题意模拟即可。
【代码】
class Solution {
public:bool isValidSudoku(vector<vector<char>>& board) {bool st[10];for (int i = 0; i < 9; i++){memset(st, false, sizeof st);for (int j = 0; j < 9; j++)if (board[i][j] == '.') continue;else if (st[board[i][j] - '0']) return false;else st[board[i][j] - '0'] = true;}for (int i = 0; i < 9; i++){memset(st, false, sizeof st);for (int j = 0; j < 9; j++)if (board[j][i] == '.') continue;else if (st[board[j][i] - '0']) return false;else st[board[j][i] - '0'] = true;}for (int i = 0; i < 9; i += 3) // 枚举每个3*3方格的左上角坐标for (int j = 0; j < 9; j += 3){memset(st, false, sizeof st);for (int x = i; x < i + 3; x++) // 枚举每个3*3方格中每个点的坐标for (int y = j; y < j + 3; y++)if (board[x][y] == '.') continue;else if (st[board[x][y] - '0']) return false;else st[board[x][y] - '0'] = true;}return true;}
};
LeetCode 37. 解数独(困难)
【题目描述】
编写一个程序,通过填充空格来解决数独问题。
数独的解法需遵循如下规则:
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次(请参考示例图)。
数独部分空格内已填入了数字,空白格用 '.' 表示。
【示例1】

输入:board =
输入:board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
输出:[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
【提示】
b o a r d . l e n g t h = = 9 board.length == 9 board.length==9
b o a r d [ i ] . l e n g t h = = 9 board[i].length == 9 board[i].length==9
board[i][j] 是一位数字(1-9)或者 '.'
题目数据保证输入数独仅有一个解
【分析】
类似 N 皇后问题,爆搜每个位置可以填入的数,我们需要使用三个数组:row[i][x]、col[i][x]、cell[i][j][x],分别表示第 i i i 行(列)是否已经存在数字 x x x 以及第 i , j i,j i,j(左上角坐标)个3*3小方格是否已经存在数字 x x x。
【代码】
class Solution {
public:bool row[9][9], col[9][9], cell[3][3][9];void solveSudoku(vector<vector<char>>& board) {memset(row, false, sizeof row);memset(col, false, sizeof col);memset(cell, false, sizeof cell);for (int i = 0; i < 9; i++)for (int j = 0; j < 9; j++)if (board[i][j] == '.') continue;else{int t = board[i][j] - '1'; // 将'1'-'9'映射为0-8row[i][t] = col[j][t] = cell[i / 3][j / 3][t] = true;}dfs(board, 0, 0); // 从第0行第0列开始搜索}bool dfs(vector<vector<char>>& board, int x, int y){if (x == 9) return true; // 搜完了所有位置,找到解if (y == 9) return dfs(board, x + 1, 0); // 搜完了一行,x加一y清零if (board[x][y] != '.') return dfs(board, x, y + 1); // 该位置已经有数直接跳过for (int i = 0; i < 9; i++)if (!row[x][i] && !col[y][i] && !cell[x / 3][y / 3][i]){board[x][y] = i + '1';row[x][i] = col[y][i] = cell[x / 3][y / 3][i] = true;if (dfs(board, x, y + 1)) return true; // 注意不能写return dfs(board, x, y + 1);board[x][y] = '.'; // 还原现场row[x][i] = col[y][i] = cell[x / 3][y / 3][i] = false;}return false; // 该位置已经用完了所有数,返回false}
};
LeetCode 38. 外观数列(中等)
【题目描述】
给定一个正整数 n,输出外观数列的第 n 项。
外观数列是一个整数序列,从数字 1 开始,序列中的每一项都是对前一项的描述。
你可以将其视作是由递归公式定义的数字字符串序列:
countAndSay(1) = "1"countAndSay(n)是对countAndSay(n-1)的描述,然后转换成另一个数字字符串。
前五项如下:
1. 1
2. 11
3. 21
4. 1211
5. 111221
第一项是数字 1
描述前一项,这个数是 1 即 “ 一 个 1 ”,记作 "11"
描述前一项,这个数是 11 即 “ 二 个 1 ” ,记作 "21"
描述前一项,这个数是 21 即 “ 一 个 2 + 一 个 1 ” ,记作 "1211"
描述前一项,这个数是 1211 即 “ 一 个 1 + 一 个 2 + 二 个 1 ” ,记作 "111221"
要描述一个数字字符串,首先要将字符串分割为最小数量的组,每个组都由连续的最多相同字符组成。然后对于每个组,先描述字符的数量,然后描述字符,形成一个描述组。要将描述转换为数字字符串,先将每组中的字符数量用数字替换,再将所有描述组连接起来。
例如,数字字符串 "3322251" 的描述如下图:

【示例1】
输入:n = 1
输出:"1"
解释:这是一个基本样例。
【示例2】
输入:n = 4
输出:"1211"
解释:
countAndSay(1) = "1"
countAndSay(2) = 读 "1" = 一 个 1 = "11"
countAndSay(3) = 读 "11" = 二 个 1 = "21"
countAndSay(4) = 读 "21" = 一 个 2 + 一 个 1 = "12" + "11" = "1211"
【提示】
1 ≤ n ≤ 30 1\le n\le 30 1≤n≤30
【分析】
直接按题意模拟即可。
【代码】
class Solution {
public:string countAndSay(int n) {string s = "1"; // 初始化for (int i = 0; i < n - 1; i++) // 需要变换n-1次{string t;for (int j = 0, k; j < s.size(); j = k){k = j + 1;while (k < s.size() && s[k] == s[k - 1]) k++; // 找到第一个不同的数t += to_string(k - j) + s[j]; // 一共k-j个s[j]}s = t;}return s;}
};
LeetCode 39. 组合总和(中等)
【题目描述】
给你一个无重复元素的整数数组 candidates 和一个目标整数 target,找出 candidates 中可以使数字和为目标数 target 的所有不同组合 ,并以列表形式返回。你可以按任意顺序返回这些组合。
candidates 中的同一个数字可以无限制重复被选取。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
【示例1】
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
【示例2】
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
【示例3】
输入: candidates = [2], target = 1
输出: []
【提示】
1 ≤ c a n d i d a t e s . l e n g t h ≤ 30 1\le candidates.length\le 30 1≤candidates.length≤30
2 ≤ c a n d i d a t e s [ i ] ≤ 40 2\le candidates[i]\le 40 2≤candidates[i]≤40
candidates 的所有元素互不相同
1 ≤ t a r g e t ≤ 40 1\le target\le 40 1≤target≤40
【分析】
本题要求出所有的方案,因此考虑可以使用爆搜。枚举每个数选不同的数量,若当前组合方案的和超过 target 了则直接剪枝。此外,由于相同的组合调换顺序不属于新的组合,因此爆搜的时候还需要保证顺序关系保证一种组合固定以一种顺序出现一次,而不会重复。
【代码】
class Solution {
public:vector<vector<int>> res;vector<int> v;vector<vector<int>> combinationSum(vector<int>& candidates, int target) {dfs(candidates, 0, target);return res;}// now表示从第几个数开始选,因为序列不能重复,例如[2,2,3]和[2,3,2]是一样的// target每次减去选中的数,减为0说明找到和恰好为target的序列void dfs(vector<int>& c, int now, int target){if (target <= 0) // 剪枝{if (target == 0) res.push_back(v); // 找到一个合法序列return;}for (int i = now; i < c.size(); i++) // 每次dfs都可以选一次now{v.push_back(c[i]);dfs(c, i, target - c[i]);v.pop_back(); // 还原现场}}
};
LeetCode 40. 组合总和 II(中等)
【题目描述】
给定一个候选人编号的集合 candidates 和一个目标数 target,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
注意:解集不能包含重复的组合。
【示例1】
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
【示例2】
输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]
【提示】
1 ≤ c a n d i d a t e s . l e n g t h ≤ 100 1\le candidates.length\le 100 1≤candidates.length≤100
1 ≤ c a n d i d a t e s [ i ] ≤ 50 1\le candidates[i]\le 50 1≤candidates[i]≤50
1 ≤ t a r g e t ≤ 30 1\le target\le 30 1≤target≤30
【分析】
与上一题基本一样,唯一区别在于每个元素只能选一次,因此每个数能选择的次数的上限是固定的,我们可以先将数组排好序,搜索的时候每次先求出每个数出现的次数,然后枚举每个数选择的次数即可。
【代码】
class Solution {
public:vector<vector<int>> res;vector<int> v;vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(), candidates.end());dfs(candidates, 0, target);return res;}void dfs(vector<int>& c, int now, int target){if (target == 0) { res.push_back(v); return; }if (now == c.size()) return; // 已经遍历完所有数int k = now + 1; // 找到第一个不相同数的下标while (k < c.size() && c[k] == c[now]) k++;int cnt = k - now; // 一共有k-now个数相同for (int i = 0; i <= cnt && c[now] * i <= target; i++) // 枚举c[now]选几个{dfs(c, k, target - c[now] * i); // 下一个位置是下一个不同的数,也就是kv.push_back(c[now]); // 注意刚开始是选0个,因此先搜索完才选c[now]}for (int i = 0; i <= cnt && c[now] * i <= target; i++)v.pop_back(); // 还原现场}
};
相关文章:

【LeetCode算法系列题解】第36~40题
CONTENTS LeetCode 36. 有效的数独(中等)LeetCode 37. 解数独(困难)LeetCode 38. 外观数列(中等)LeetCode 39. 组合总和(中等)LeetCode 40. 组合总和 II(中等)…...
java+ssm+mysql电梯管理系统
项目介绍: 使用javassmmysql开发的电梯管理系统,系统包含管理员,监管员、安全员、维保员角色,功能如下: 管理员:系统用户管理(监管员、安全员、维保员);系统公告&#…...

最近读书了吗?林曦老师与你分享来自暄桐课堂的读书方法
近来,大家有在开心读书吗?对于读书,有一个很生动的说法:“无事常读书,一日是四日。若活七十年,便二百八十。”读书帮助我们超越个体生命经验的限制,此时此地的我们,也可借由书本&…...
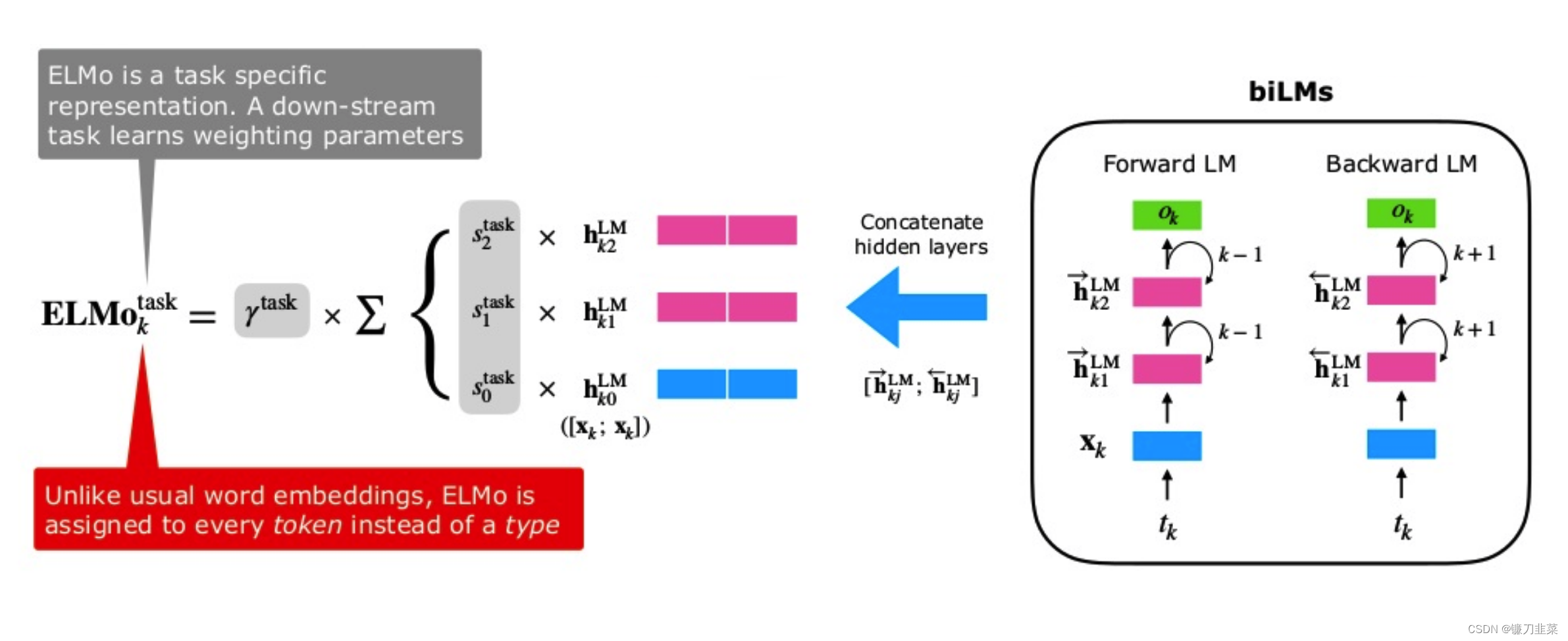
【AI理论学习】语言模型:从Word Embedding到ELMo
语言模型:从Word Embedding到ELMo ELMo原理Bi-LM总结参考资料 本文主要介绍一种建立在LSTM基础上的ELMo预训练模型。2013年的Word2Vec及2014年的GloVe的工作中,每个词对应一个vector,对于多义词无能为力。ELMo的工作对于此,提出了…...

多功能透明屏,在智能家居领域中,有哪些功能特点?显示、连接
多功能透明屏是一种新型的显示技术,它能够在透明的表面上显示图像和视频,并且具有多种功能。 这种屏幕可以应用于各种领域,如商业广告、智能家居、教育等,为用户提供更加便捷和多样化的体验。 首先,多功能透明屏可以…...
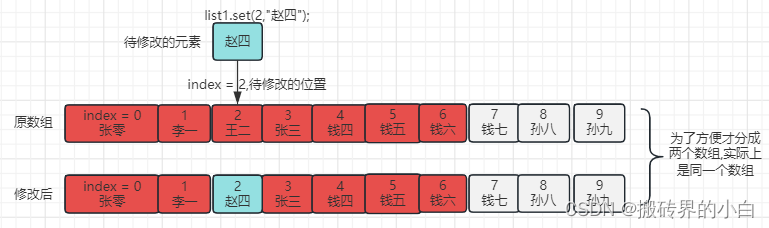
【List篇】ArrayList 详解(含图示说明)
Java中的ArrayList是一个动态数组,可以自动扩展容量以适应数据的添加和删除。它可以用来存储各种类型的数据,例如String,Integer,Boolean等。ArrayList实现了List接口,可以进行常见的List操作,例如添加、插…...

SSL证书只有收费的吗?有没有免费使用的?
首先明白SSL证书是什么SSL英文全称:英文全称: Secure Socket Layer Certificate,中文全称:安全套接字层证书。 SSL是一种由数字证书颁发机构(CA) 签发的数字证书。它用于建立安全的加密连接,确保通过网络传输的数据在客户端和服务器之间的安全性和完整性…...

48V轻混技术
文章目录 48V轻混技术的主要特点和优势48V轻混技术的优缺点优点:缺点: 48V轻混技术的主要特点和优势 48V轻混技术(48V Mild Hybrid Technology)是一种汽车动力系统技术,它结合了内燃机和电动机的优势,以提…...

机器学习基础算法--回归类型和评价分析
目录 1.数据归一化处理 2.数据标准化处理 3.Lasso回归模型 4.岭回归模型 5.评价指标计算 1.数据归一化处理 """ x的归一化的方法还是比较多的我们就选取最为基本的归一化方法 x(x-x_min)/(x_max-x_min) """ import numpy as np from sklea…...

MATLAB 软件功能简介
MATLAB 的名称源自 Matrix Laboratory,1984 年由美国 Mathworks 公司推向市场。 它是一种科学计算软件,专门以矩阵的形式处理数据。MATLAB 将高性能的数值计算和可 视化集成在一起,并提供了大量的内置函数,从而被广泛的应用于科学计算、控制…...
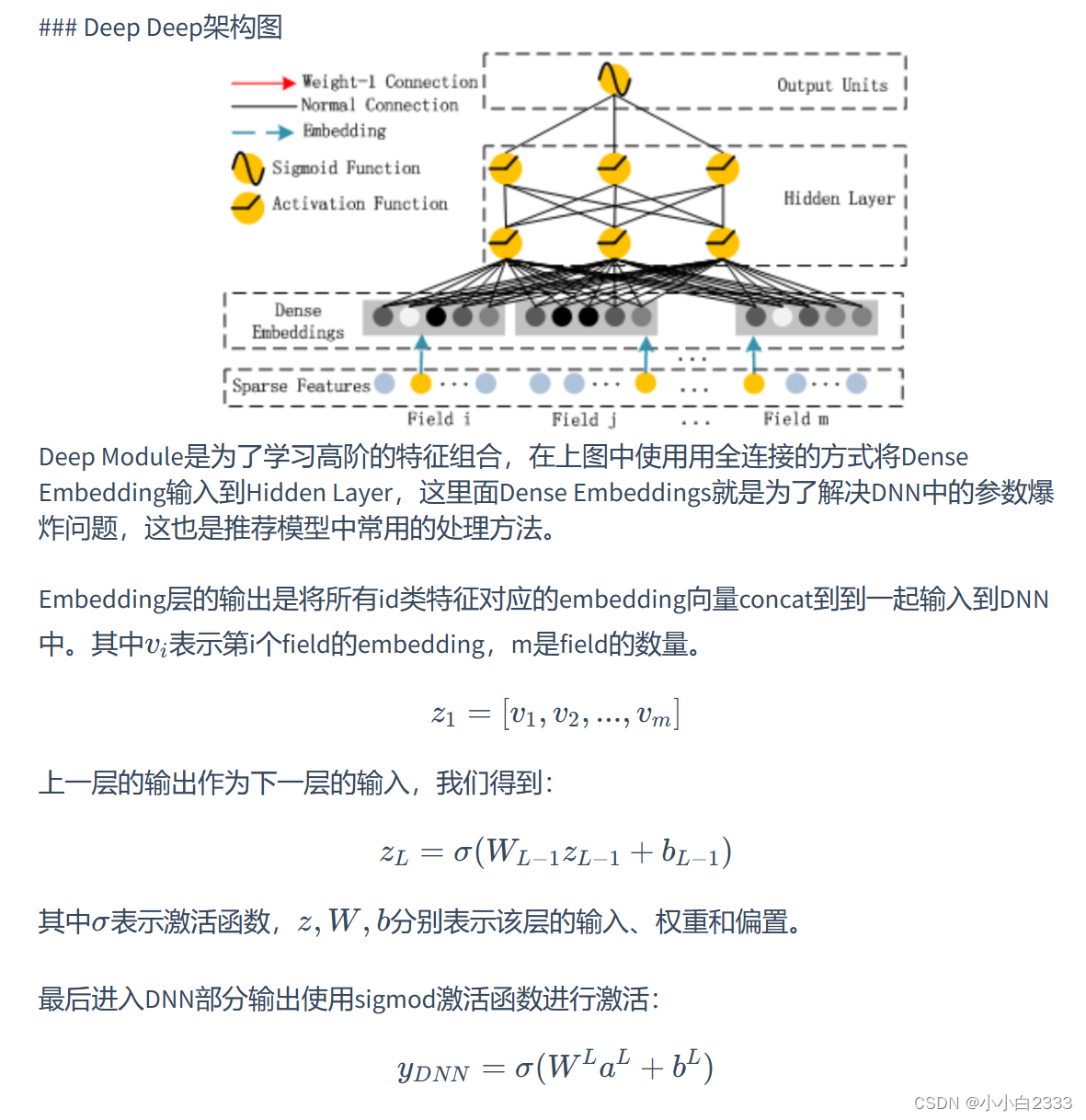
deepfm内容理解
对于CTR问题,被证明的最有效的提升任务表现的策略是特征组合(Feature Interaction); 两个问题: 如何更好地学习特征组合,进而更加精确地描述数据的特点; 如何更高效的学习特征组合。 DNN局限 :当我们使…...
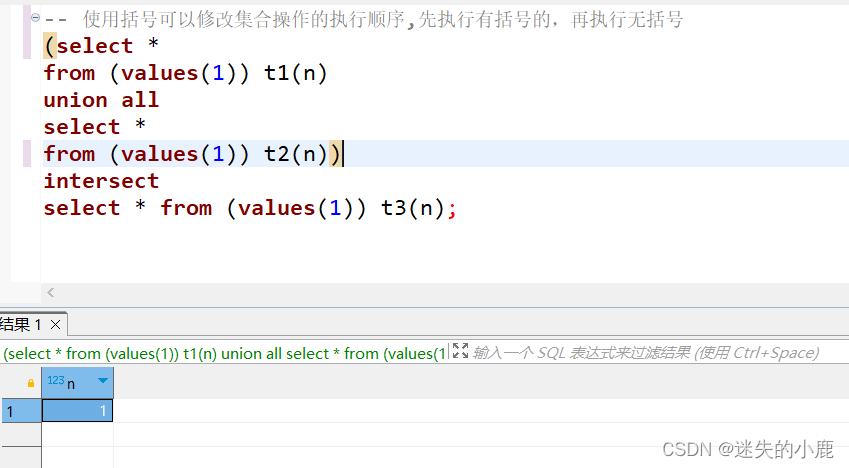
postgresql-集合运算
postgresql-集合运算 并集交集差集集合运算符的优先级 并集 create table excellent_emp( year int not null, emp_id integer not null, constraint pk_excellent_emp primary key(year,emp_id) );insert into excellent_emp values(2018,9); insert into excellent_emp value…...

[持续更新]计算机经典面试题基础篇Day2
[通用]计算机经典面试题基础篇Day2 1、单例模式是什么,线程安全吗 单例模式是一种设计模式,旨在确保一个类只有一个实例,并提供全局访问点。通过使用单例模式,可以避免多次创建相同的对象,节省内存资源,同…...

C++:类和对象(二)
本文主要介绍:构造函数、析构函数、拷贝构造函数、赋值运算符重载、const成员函数、取地址及const取地址操作符重载。 目录 一、类的六个默认成员函数 二、构造函数 1.概念 2.特性 三、析构函数 1.概念 2.特性 四、拷贝构造函数 1.概念 2.特征 五、赋值…...
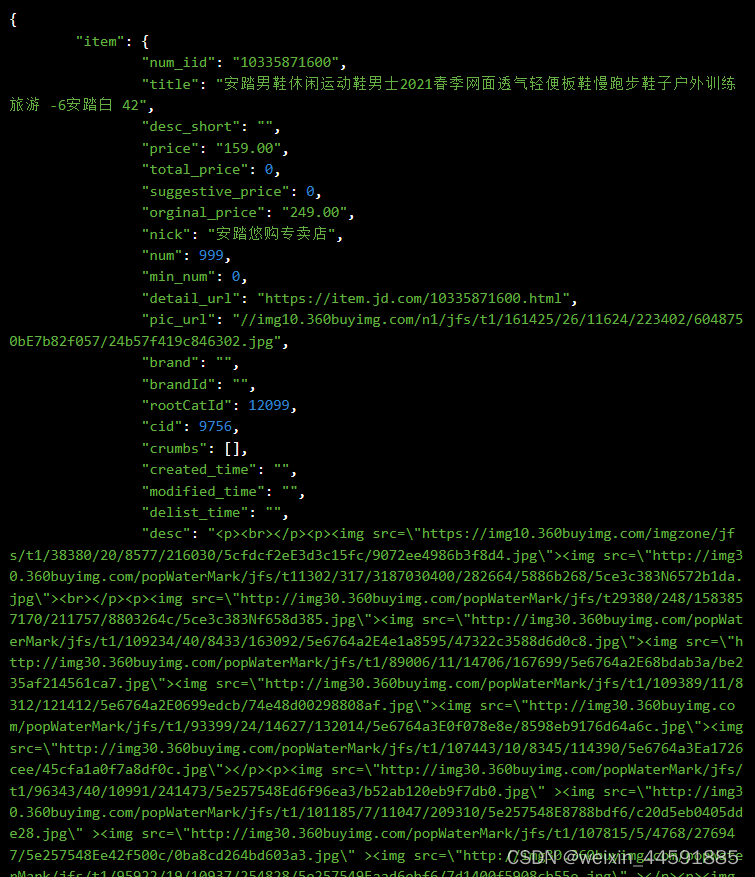
Java“牵手”京东商品详情数据,京东商品详情API接口,京东API接口申请指南
京东平台商品详情接口是开放平台提供的一种API接口,通过调用API接口,开发者可以获取京东商品的标题、价格、库存、月销量、总销量、库存、详情描述、图片等详细信息 。 获取商品详情接口API是一种用于获取电商平台上商品详情数据的接口,通过…...

Fluidd摄像头公网无法正常显示修复一例
Fluidd摄像头在内网正常显示,公网一直无法显示,经过排查发现由于url加了端口号引起的,摄像头url中正常填写的是/webcam?actionsnapshot,或者/webcam?actionstream。但是由于nginx跳转机制,会被301跳转到/webcam/?ac…...
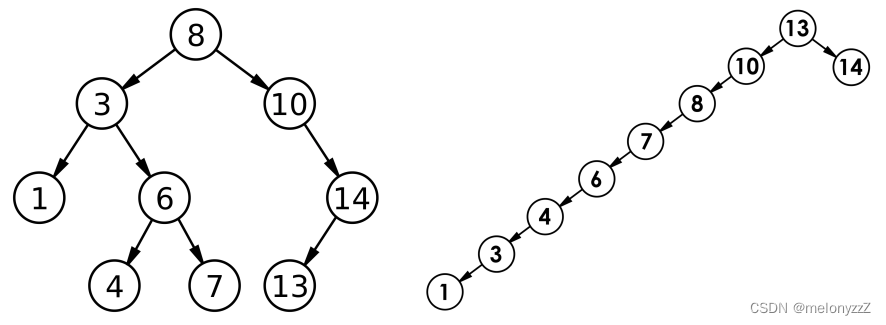
【C++ 学习 ⑳】- 详解二叉搜索树
目录 一、概念 二、实现 2.1 - BST.h 2.2 - test.cpp 三、应用 四、性能分析 一、概念 二叉搜索树(BST,Binary Search Tree),又称二叉排序树或二叉查找树。 二叉搜索树是一棵二叉树,可以为空;如果不…...
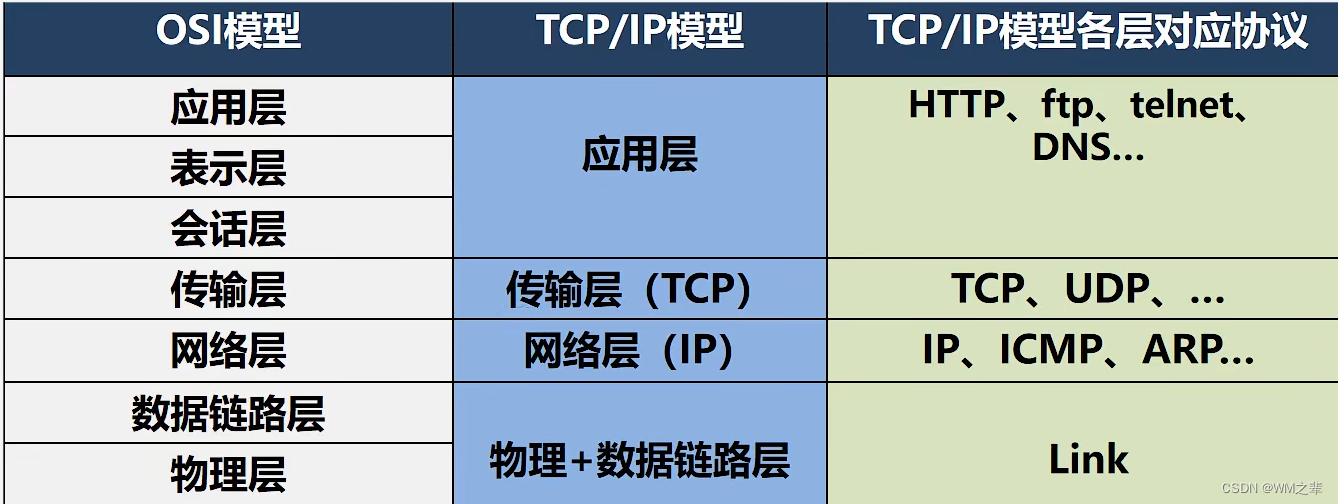
Java中网络的基本介绍。网络通信,网络,ip地址,域名,端口,网络通信协议,TCP/IP传输过程,网络通信协议模型,TCP协议,UDP协议
- 网络通信 概念:网络通信是指通过计算机网络进行信息传输的过程,包括数据传输、语音通话、视频会议等。在网络通信中,数据被分成一系列的数据包,并通过网络传输到目的地。在数据传输过程中,需要确保数据的完整性、准…...

【Qt】总体把握文本编码问题
在项目开发中,经常会遇到文本编码问题。文本编码知识非常基础,但对于新手来说,可能需要花费较长的时间去尝试,才能在脑海中建立对编码的正确认知。文本编码原理并不难,难的是在项目实践中掌握正确处理文本编码的方法。…...
之curl)
Linux命令(77)之curl
linux命令之curl 1.curl介绍 linux命令之curl是一款强大的http命令行工具,它支持文件的上传和下载,是综合传输工具。 2.curl用法 curl [参数] [url] curl参数 参数说明-C断点续传-o <filename>把输出写到filename文件中-x在给定的端口上使用HT…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
