Windows平台Fortran编程入门
Fortran,原意为 Formula Translation(公式翻译器);一门出现很早的面向科学计算的高级语言,在数值计算领域仍然使用;
免费 Fortran 的编译器包括 GCC 的 GFortran,Intel 的 Intel Fortran Compiler 等;
下面看一下一个小巧的Fortran编译器G95;
安装以后,把G95的bin目录加入path环境变量;

新建如下的环境变量;

做一个简单程序,保存为test1.f90,
program addNumbers
! This simple program adds two numbersimplicit none
! Type declarationsreal :: a, b, result
! Executable statementsa = 12.0b = 15.0result = a + bprint *, 'The total is ', result
end program addNumbers构建运行如下;

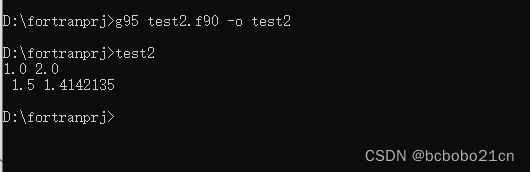
再做一个test2.f90,
PROGRAM Example_1_1 ! 求两种平均値REAL :: a, b, av1, av2READ *, a, bav1 = (a + b)/2; av2 = (a*b)**0.5PRINT *, av1, av2
END构建运行如下;输入2个数,然后计算;
没有分类,先放到matlab里面;
相关文章:

Windows平台Fortran编程入门
Fortran,原意为 Formula Translation(公式翻译器);一门出现很早的面向科学计算的高级语言,在数值计算领域仍然使用; 免费 Fortran 的编译器包括 GCC 的 GFortran,Intel 的 Intel Fortran Compi…...

05-Mysql夺命三连问:什么是索引下推?什么是索引覆盖?什么是回表?【Java面试总结】
Mysql夺命三连问:什么是索引下推?什么是索引覆盖?什么是回表? 索引下推是mysql5.6 提出的一个查询优化方案,主要的目的是减少数据或查询中不必要的读取和计算,它的原理是将查询条件尽可能的推送到索引层面…...
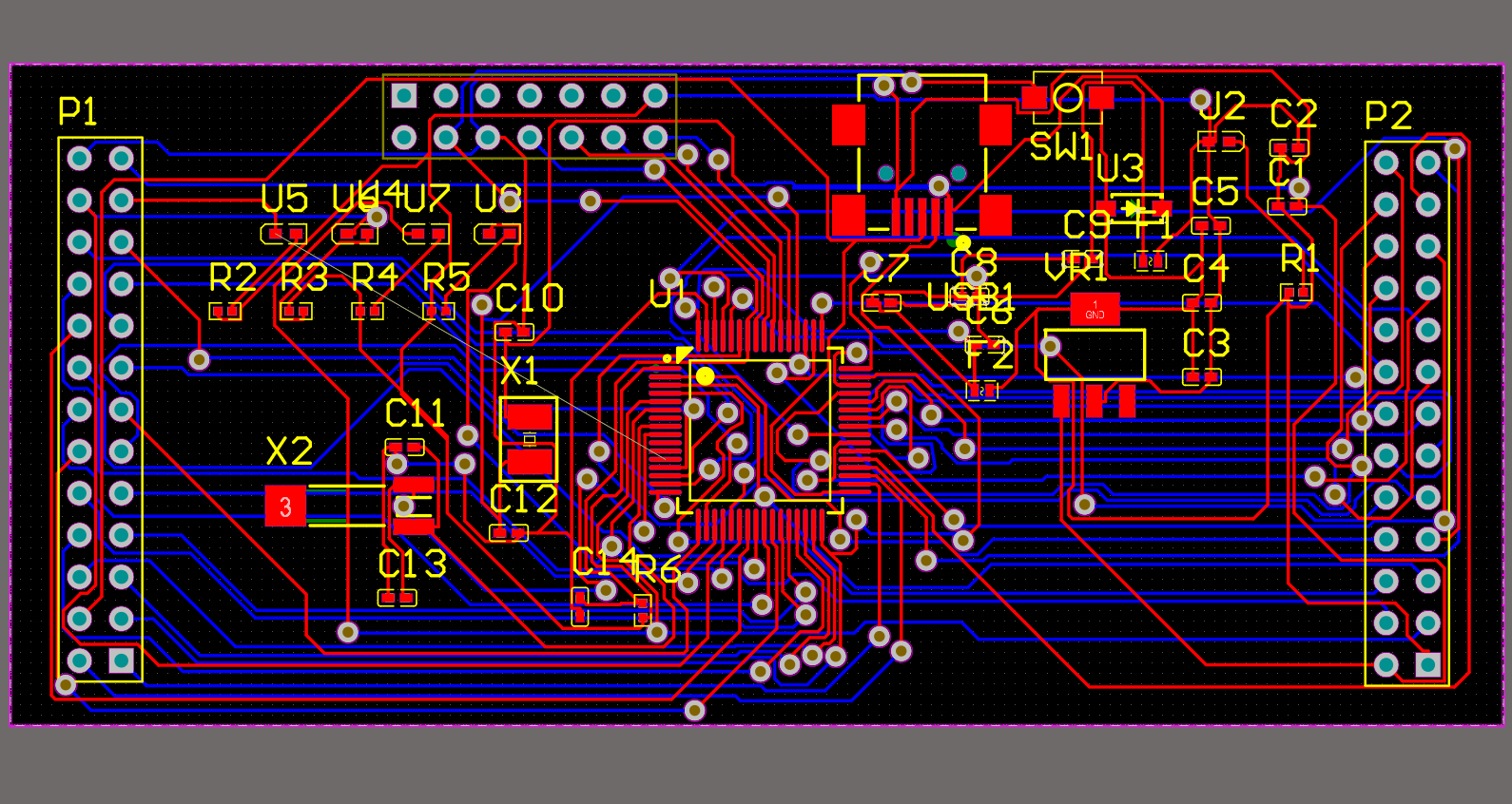
晨启,MSP430开发板,51开发板,原理图,PCB图
下载:https://github.com/xddun/blog_code_search...

Notepad++ 的安装及配置
由于电脑重装了Win11系统,干脆重头开始,重新安装每一个软件~~~ 很多博客或者博主都会推荐notepad的官网:https://notepad-plus-plus.org/ 但大家亲自点开就会发现是无响应,如下图 同时,也会有很多博主直接给网盘地址…...

✔ ★算法基础笔记(Acwing)(一)—— 基础算法(20道题)【java版本】
基础算法 一、快速排序1. 快速排序例题2. 第k个数( 快速选择 ) ✔ ✔1.31★快排二刷总结( 4点 ) 二、归并排序1. 归并排序模板题 ✔ ✔1.31★二刷总结 ★2. 逆序对的数量 ✔ ✔1.31★二刷总结 三、二分1. 数的范围 ✔1.31★二刷总结(mid > x 则是 输出最左边一个)第一个大于…...

简单记录下gin中使用中间件记录操作日志
1、直接定义中间件package middlewareimport ("bytes""encoding/json""fmt""github.com/gin-gonic/gin""go.uber.org/zap""io""strconv""strings" )func LoggerMiddleWare() gin.HandlerFunc…...
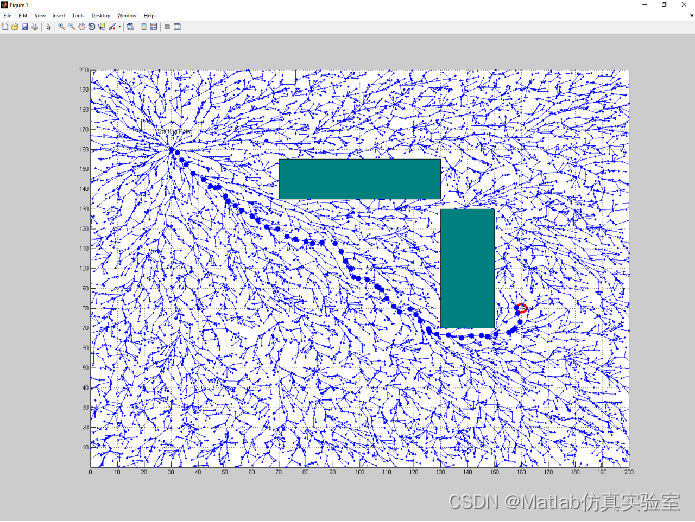
基于Matlab利用IRM和RRTstar实现无人机路径规划(附上源码+数据+说明+报告+PPT)
无人机路径规划是无人机应用领域中的关键问题之一。本文提出了一种基于IRM(Informed RRTstar Method)和RRTstar(Rapidly-exploring Random Tree star)算法的无人机路径规划方法,并使用Matlab进行实现。该方法通过结合I…...

uniapp使用@microsoft/signalr(报错“ReferenceError: require is not defined“)
后台老哥要用微软的signalr,总结了一些经验和问题 引入方法 1、npm npm i microsoft/signalr 2、下载他的js或者cdn <script src"https://cdnjs.cloudflare.com/ajax/libs/microsoft-signalr/6.0.1/signalr.js"></script>在uniapp中&…...

CloudCompare 二次开发(9)——半径滤波
目录 一、概述二、代码集成三、结果展示本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫。 一、概述 使用CloudCompare与PCL的混合编程实现点云半径滤波。半径滤波的算法原理见:PCL 半径滤波器。基于PCL将半径滤波集成到Cl…...

ElementUI浅尝辄止29:Breadcrumb 面包屑
显示当前页面的路径,快速返回之前的任意页面。 1.如何使用? 在el-breadcrumb中使用el-breadcrumb-item标签表示从首页开始的每一级。Element 提供了一个separator属性,在el-breadcrumb标签中设置它来决定分隔符,它只能是字符串&am…...

ABB MPRC086444-005数字输入模块
ABB MPRC086444-005 是一款数字输入模块,通常用于工业自动化和控制系统中,用于接收和处理数字信号。以下是这种类型的数字输入模块通常可能具备的一般功能和特点: 数字输入接口:MPRC086444-005 模块通常配备多个数字输入通道&…...

stable diffusion实践操作-常见lora模型介绍
系列文章目录 本文专门开一节写Lora相关的内容,在看之前,可以同步关注: stable diffusion实践操作 文章目录 系列文章目录前言一、什么是lora?1.1 lora 定义1.2 lora的基本原理1.2 通过分层控制lora 二、作用:2.1 复刻人物特征2…...
kubeadm 安装k8s
目录 安装k8s 环境准备 所有节点,关闭防火墙规则,关闭selinux,关闭swap交换(必须关闭swap分区) //修改主机名 //所有节点修改hosts文件 //调整内核参数 所有节点安装docker 所有节点安装kubeadm,kube…...

选择最适合您的Bug管理软件:市场比较与推荐
“Bug管理软件哪家好?市场上有许多优秀的Bug管理系统品牌如:Zoho Projects、JIRA、Redmine、Bugzilla、MantisBT。” 一款高效的Bug管理系统可以帮助团队更有效地发现、记录和解决软件中的问题,从而提高产品质量和用户满意度。本文将为您介绍…...
Spring MVC的常用注解及用法
Spring MVC的执行流程: 1.用户的请求首先到Controller 2.Controller将请求转发给Model 3.Model处理业务并将数据结果给Controller 4.Controller会将数据给View引擎 5.View转换数据生成最终的页面给用户。 常用注解: 1.requestMapping:…...

HTTP和HTTPS的区别、 HTTPS运行原理
HTTP 一种用于web浏览器和web服务器基于数据传递的协议基于TCP/IP协议的应用层传送,用于客户端和服务器之间的数据交互 HTTPS 是HTTP的安全版,基于SSL或TLS协议,对客户端和服务器之间加密和身份验证,使得数据之间传递具有了安全…...

统计封闭岛屿的数目
1254. 统计封闭岛屿的数目 关于岛屿的相似题目: 岛屿数量 – 二维矩阵的dfs算法封闭岛屿数量 – 二维矩阵的dfs算法统计封闭岛屿的数目统计子岛屿不同岛屿的数量 class MaxAreaOfIsland:"""floodFill 算法1254. 统计封闭岛屿的数目https://leetcod…...

【数据结构与算法系列4】长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl1, ..., numsr-1, numsr] ,并返回其长度**。**如果不存在符合条件的子数组,返回 0 。 示例 1: 输入&…...

问道管理:底部渐渐抬高 今年反弹时刻或已来临
快速探底后,两市呈现分解走势。 沪指周三低开震动,指数在20日均线取得支撑后小幅上升,最终以红盘报收。深成指走势弱于沪指,尽管午后指数有所上升,但最终未能翻红。到收盘,沪指报收3158.08点,上…...

正规黄金代理的三大要素
对于现货黄金投资来说,寻找一个正规的黄金代理是十分重要的问题。在目前的现货黄金投资市场中,现货黄金代理的数量很多,他们都致力于耕耘现货黄金投资市场。当越来越多的专业人士加入到现货黄金投资的市场中当中时,这个市场将会越…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...
