软考高级系统架构设计师系列案例考点专题三:数据库系统考点梳理及精讲
软考高级系统架构设计师系列案例考点专题三:数据库系统考点梳理及精讲
- 一、ORM技术
- 二、数据库分类比较
- 三、并发控制
- 四、封锁协议
- 五、不规范化带来的四大问题
- 六、反规范化技术
- 七、分布式数据库
- 八、数据仓库集成
数据库系统知识在架构设计师的考试里时有考查,主要考查的是数据库的一些新技术的比较,如关系型数据库、内存数据库及NoSQL等,很少涉及到规范化,但也要掌握。
一、ORM技术
- ORM,即Object-Relational Mapping,它在关系型数据库和对象之间作一个映像,这样,在具体操作数据库的时候,就不需要再去和复杂的SQL语句打交道,只要像平时操作对象一样操作即可。
- 面向对象编程把所有实体看成对象(object),关系型数据库则是采用实体之间的关系连接数据。很早就有人提出,关系也可以用对象表达,这样,就能使用面向对象编程来操作关系型数据库。
ORM把数据库映像成对象,如:
- 数据库的表table = 类 class
- 记录 = 对象
- 字段 = 对象的属性
ORM的优点:
- 使用
相关文章:

软考高级系统架构设计师系列案例考点专题三:数据库系统考点梳理及精讲
软考高级系统架构设计师系列案例考点专题三:数据库系统考点梳理及精讲 一、ORM技术二、数据库分类比较三、并发控制四、封锁协议五、不规范化带来的四大问题六、反规范化技术七、分布式数据库八、数据仓库集成数据库系统知识在架构设计师的考试里时有考查,主要考查的是数据库…...

【 XXL-JOB】 XXL-JOB任务分片
文章目录 前言xxl-job 分片广播任务的详细教程创建任务编写任务代码分片参数设置执行任务查看任务执行结果示例1示例2 总结 前言 xxl-job 是一个分布式任务调度平台,支持定时任务和分片任务。其中,分片任务可以将一个大任务拆分成多个小任务,…...

RK3568开发笔记-SATA接口调试
目录 前言 一、sata接口介绍 物理连接 数据传输速度...

异步编程 - 09 Spring框架中的异步执行_@Async注解异步执行原理源码解析
文章目录 概述小结好文推荐 概述 在Spring中调用线程将在调用含有Async注释的方法时立即返回,Spring是如何做到的呢?其实是其对标注Async注解的类做了代理,比如下面的类Async-AnnotationExample。 public class AsyncAnnotationExample {As…...

django-项目
一、RESTful设计风格 基础概念 全称:Representational State Transfer 1.资源 网络上的一个实体,每个资源都有一个独一无二的URL与之对应;获取资源-直接访问URL即可 2.表现层 资源的表现形式 如HTML、xml、JPG、json等 3.状态转化 …...
红日靶场五(vulnstack5)渗透分析
环境搭建 win7 192.168.111.132(仅主机) 192.168.123.212(桥接) .\heart p-0p-0p-0win2008 ip: 192.168.111.131(仅主机) sun\admin 2020.comkali ip: 192.168.10.131(nat)vps&…...

掌握Gitflow的一些进阶用法
1、自定义分支命名约定: 默认情况下,GitFlow使用一套分支命名约定,如feature/、release/和hotfix/等前缀。然而,你可以根据项目的需求自定义分支名称。例如,你可以在分支名称中包含项目、功能或团队成员的信息&#x…...

算法随笔:各种经典最短路算法的简要比较总结
有多种最短路径的应用场景,它们需要用到不同的算法来解决。除了贪心最优搜索之外,其他都是最优性算法,即得到的解都是最短路径。其中m是边的数量,n是点的数量。 问题边权算法时间复杂度一个起点,一个终点非负数&#…...

concrt140.dll怎么下载,concrt140.dll修复工具(修复精灵下载)一键修复问题
今天,我将为大家介绍一个非常常见的问题:由于找不到concrt140.dll,无法继续执行代码怎么办。这个问题可能会让很多网友感到头疼,但是别担心,我会为大家提供5种最全详细的恢复方法。在接下来我将详细介绍这些问题及其解决方法。希望…...
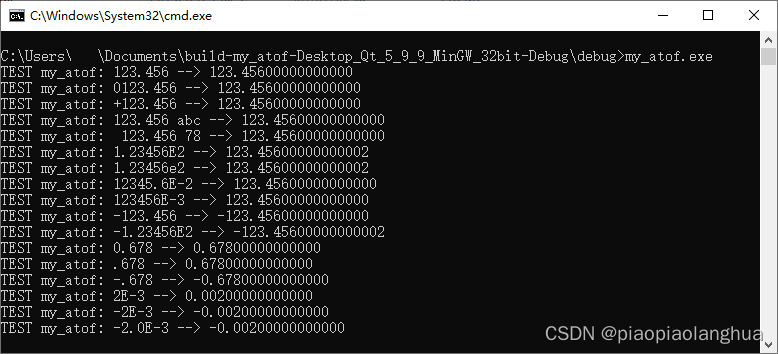
自行实现字符串转浮点数函数atof()
【重复造轮子的原因】 尽管atof是标准C中自带的函数,用于将字符串转为浮点数,但是在某些环境下有可能没法使用的(例如CUDA环境中,没有atof函数,但是math.h可以使用),因此自行实现。 【通过的测试用例】 【实现的代码】 #include <stdio.h> #include <math.h…...
Windows平台Fortran编程入门
Fortran,原意为 Formula Translation(公式翻译器);一门出现很早的面向科学计算的高级语言,在数值计算领域仍然使用; 免费 Fortran 的编译器包括 GCC 的 GFortran,Intel 的 Intel Fortran Compi…...

05-Mysql夺命三连问:什么是索引下推?什么是索引覆盖?什么是回表?【Java面试总结】
Mysql夺命三连问:什么是索引下推?什么是索引覆盖?什么是回表? 索引下推是mysql5.6 提出的一个查询优化方案,主要的目的是减少数据或查询中不必要的读取和计算,它的原理是将查询条件尽可能的推送到索引层面…...
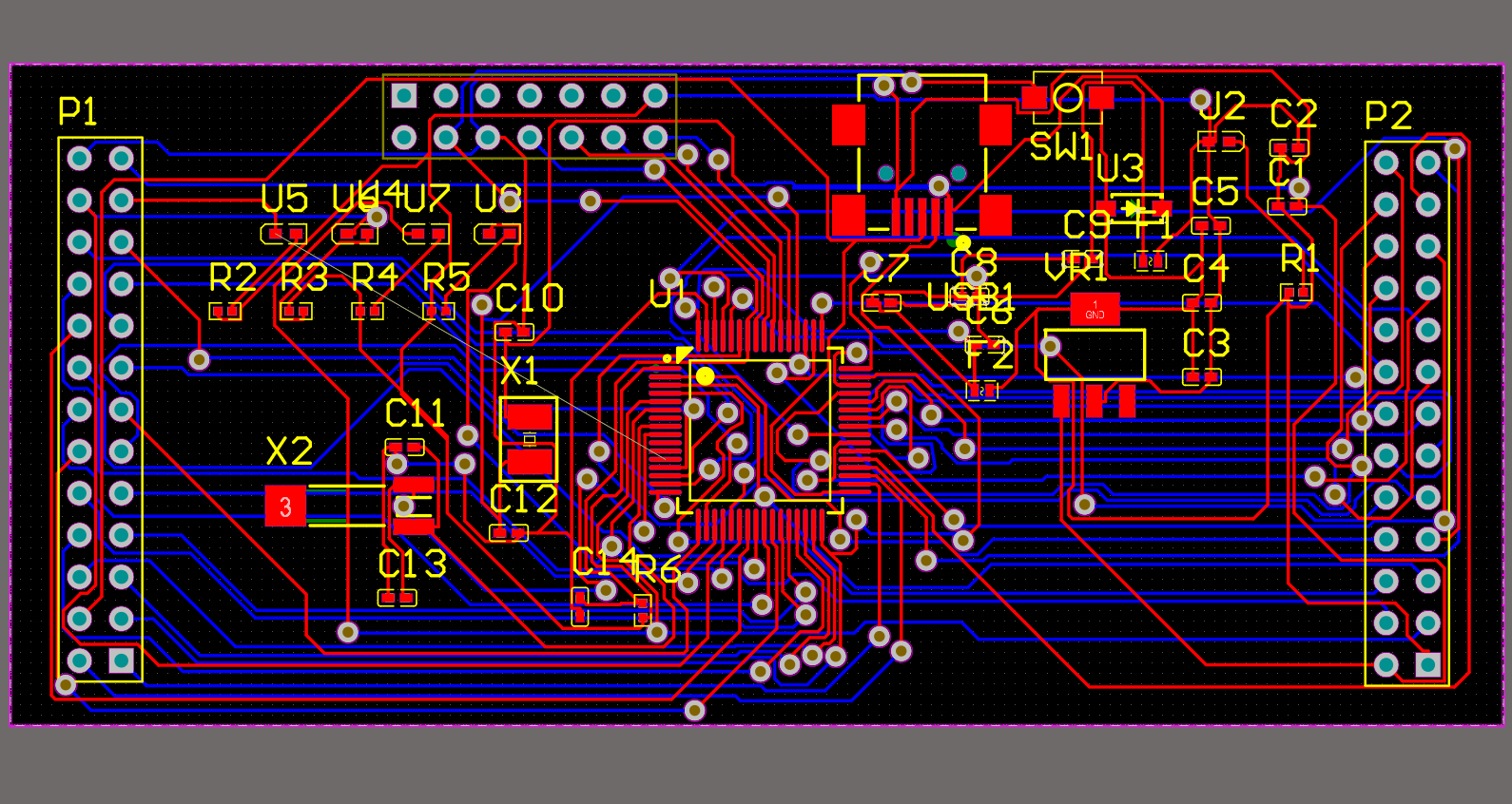
晨启,MSP430开发板,51开发板,原理图,PCB图
下载:https://github.com/xddun/blog_code_search...

Notepad++ 的安装及配置
由于电脑重装了Win11系统,干脆重头开始,重新安装每一个软件~~~ 很多博客或者博主都会推荐notepad的官网:https://notepad-plus-plus.org/ 但大家亲自点开就会发现是无响应,如下图 同时,也会有很多博主直接给网盘地址…...

✔ ★算法基础笔记(Acwing)(一)—— 基础算法(20道题)【java版本】
基础算法 一、快速排序1. 快速排序例题2. 第k个数( 快速选择 ) ✔ ✔1.31★快排二刷总结( 4点 ) 二、归并排序1. 归并排序模板题 ✔ ✔1.31★二刷总结 ★2. 逆序对的数量 ✔ ✔1.31★二刷总结 三、二分1. 数的范围 ✔1.31★二刷总结(mid > x 则是 输出最左边一个)第一个大于…...

简单记录下gin中使用中间件记录操作日志
1、直接定义中间件package middlewareimport ("bytes""encoding/json""fmt""github.com/gin-gonic/gin""go.uber.org/zap""io""strconv""strings" )func LoggerMiddleWare() gin.HandlerFunc…...
基于Matlab利用IRM和RRTstar实现无人机路径规划(附上源码+数据+说明+报告+PPT)
无人机路径规划是无人机应用领域中的关键问题之一。本文提出了一种基于IRM(Informed RRTstar Method)和RRTstar(Rapidly-exploring Random Tree star)算法的无人机路径规划方法,并使用Matlab进行实现。该方法通过结合I…...

uniapp使用@microsoft/signalr(报错“ReferenceError: require is not defined“)
后台老哥要用微软的signalr,总结了一些经验和问题 引入方法 1、npm npm i microsoft/signalr 2、下载他的js或者cdn <script src"https://cdnjs.cloudflare.com/ajax/libs/microsoft-signalr/6.0.1/signalr.js"></script>在uniapp中&…...

CloudCompare 二次开发(9)——半径滤波
目录 一、概述二、代码集成三、结果展示本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫。 一、概述 使用CloudCompare与PCL的混合编程实现点云半径滤波。半径滤波的算法原理见:PCL 半径滤波器。基于PCL将半径滤波集成到Cl…...

ElementUI浅尝辄止29:Breadcrumb 面包屑
显示当前页面的路径,快速返回之前的任意页面。 1.如何使用? 在el-breadcrumb中使用el-breadcrumb-item标签表示从首页开始的每一级。Element 提供了一个separator属性,在el-breadcrumb标签中设置它来决定分隔符,它只能是字符串&am…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...
