Pytorch深度学习实战3-4:通俗理解张量Tensor的爱因斯坦求和(附实例)
目录
- 1 爱因斯坦求和由来
- 2 爱因斯坦求和原理
- 3 实例:字母表示法
- 3.1 向量运算
- 3.2 矩阵运算
- 3.3 张量运算
- 4 实例:常量表示法
- 4.1 向量运算
- 4.2 矩阵运算
- 4.3 张量运算
1 爱因斯坦求和由来
爱因斯坦求和约定(Einstein summation convention)是一种标记的约定,又称为爱因斯坦标记法(Einstein notation),在处理关于坐标的方程式时非常有用。这约定是由阿尔伯特·爱因斯坦于1916年提出的。后来,爱因斯坦与友人半开玩笑地说:“这是数学史上的一大发现,若不信的话,可以试着返回那不使用这方法的古板日子。”
采用爱因斯坦求和约定,可以使数学表达式显得简洁明快。
在深度学习中经常涉及高阶张量运算,普通代数方法(如矩阵乘法)相对冗杂,因此引入爱因斯坦求和约定,其核心原理是将张量下标划分为自由标(free index)和哑标(dummy index),通过遍历自由标而对哑标逐元相乘求和的方式进行张量运算。
2 爱因斯坦求和原理
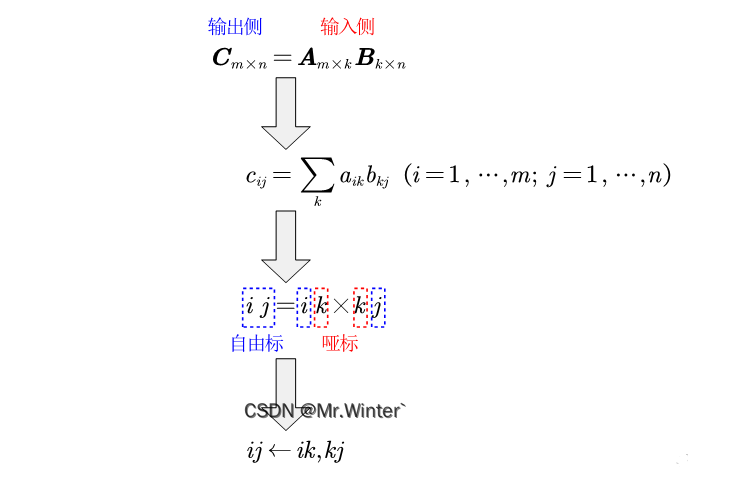
爱因斯坦求和原理并不复杂,具体而言,可以用下图来通俗理解,定义:
- 自由标:在输入输出侧都出现且各出现一次的索引号;
- 哑标:只在输入侧出现且出现两次的索引号。
输入、输出索引号的个数表示各参与运算张量的维度,例如下图表示两个二维张量做求和运算输出一个二维张量。
3 实例:字母表示法
3.1 向量运算
# ============================ 一维张量 ================================
a = torch.tensor([1, 2, 3], dtype=float)
b = torch.tensor([4, 5, 6], dtype=float)# 向量内积
print("向量内积:", torch.einsum("i, i ->", a, b))
# 向量点乘
print("向量点乘:",torch.einsum("i, i -> i", a, b))
结果如下:
>>> 向量内积: tensor(32., dtype=torch.float64)
>>> 向量点乘: tensor([ 4., 10., 18.], dtype=torch.float64)
3.2 矩阵运算
# ============================ 二维张量 ================================
c = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)
d = torch.ones((3, 4), dtype=float)# 矩阵乘法
print("矩阵乘法:", torch.einsum("ij, jk -> ik", c, d))
# 转置
print("矩阵转置:", torch.einsum("ij -> ji", c))
# 迹
print("迹:", torch.einsum("ii ->", c))
# 对角元
print("对角元:", torch.einsum("ii -> i", c))
# 矩阵按行求和
print("矩阵按行求和:", torch.einsum("ij -> j", c))
# 矩阵按列求和
print("矩阵按列求和:", torch.einsum("ij -> i", c))
# 矩阵所有元素求和
print("矩阵所有元素求和:", torch.einsum("ij ->", c))
# 矩阵乘向量
print("矩阵乘向量:", torch.einsum("ij, j -> i", c, a))
结果如下:
>>> 矩阵乘法: tensor([[ 6., 6., 6., 6.],[15., 15., 15., 15.],[24., 24., 24., 24.]], dtype=torch.float64)
>>> 矩阵转置: tensor([[1., 4., 7.],[2., 5., 8.],[3., 6., 9.]], dtype=torch.float64)
>>> 迹: tensor(15., dtype=torch.float64)
>>> 对角元: tensor([1., 5., 9.], dtype=torch.float64)
>>> 矩阵按行求和: tensor([12., 15., 18.], dtype=torch.float64)
>>> 矩阵按列求和: tensor([ 6., 15., 24.], dtype=torch.float64)
>>> 矩阵所有元素求和: tensor(45., dtype=torch.float64)
>>> 矩阵乘向量: tensor([14., 32., 50.], dtype=torch.float64)
3.3 张量运算
# ============================ 高阶张量 ================================
e = torch.arange(60.).reshape(5, 3, 4)
f = torch.arange(24.).reshape(2, 4, 3)# 三维张量压缩
print("三维张量压缩:", torch.einsum("kij, lji -> kl", e, f))
结果如下:
>>> 三维张量压缩: tensor([[ 440., 1232.],[ 1232., 3752.],[ 2024., 6272.],[ 2816., 8792.],[ 3608., 11312.]])
4 实例:常量表示法
以下结果同第三节,不再赘述
4.1 向量运算
'''
索引表示法
(张量后接输入索引, 最后是输出索引)
'''
# ============================ 一维张量 ================================
a = np.array([1, 2, 3], dtype=float)
b = np.array([4, 5, 6], dtype=float)# 向量内积
print("向量内积:", np.einsum(a, [0], b, [0]))
# 向量点乘
print("向量点乘:",np.einsum(a, [0], b, [0], [0]))
4.2 矩阵运算
# ============================ 二维张量 ================================
c = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)
d = np.ones((3, 4), dtype=float)# 矩阵乘法
print("矩阵乘法:", np.einsum(c, [0, 1], d, [1, 2], [0, 2]))
# 转置
print("矩阵转置:", np.einsum(c, [0, 1], [1, 0]))
# 迹
print("迹:", np.einsum(c, [0, 0]))
# 对角元
print("对角元:", np.einsum(c, [0, 0], [0]))
# 矩阵按行求和
print("矩阵按行求和:", np.einsum(c, [0, 1], [1]))
# 矩阵按列求和
print("矩阵按列求和:", np.einsum(c, [0, 1], [0]))
# 矩阵所有元素求和
print("矩阵所有元素求和:", np.einsum(c, [0, 1]))
# 矩阵乘向量
print("矩阵乘向量:", np.einsum(c, [0, 1], a, [1], [0]))
4.3 张量运算
# ============================ 高阶张量 ================================
e = np.arange(60.).reshape(5, 3, 4)
f = np.arange(24.).reshape(2, 4, 3)# 三维张量压缩
print("三维张量压缩:", np.einsum(e, [2, 0, 1], f, [3, 1, 0], [2, 3]))
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
相关文章:

Pytorch深度学习实战3-4:通俗理解张量Tensor的爱因斯坦求和(附实例)
目录1 爱因斯坦求和由来2 爱因斯坦求和原理3 实例:字母表示法3.1 向量运算3.2 矩阵运算3.3 张量运算4 实例:常量表示法4.1 向量运算4.2 矩阵运算4.3 张量运算1 爱因斯坦求和由来 爱因斯坦求和约定(Einstein summation convention)是一种标记的约定&#…...
GEE学习笔记 五十六:GEE中如何把文件导出到Google Drive的子目录
今天在群里看到有人在问一个问题,如何使用GEE把文件导出到Google Drive的子目录中?这里我就简单的说一下这个问题。 首先,在GEE中我们都知道了如何将数据导出导出Google Drive的文件夹中,如下面的一个例子: var geome…...

【Go基础】数据库编程
文章目录1. SQL语法简介2. MySQL最佳实践3. Go SQL驱动接口解读4. 数据库增删改查5. stmt6. SQLBuilder6.1 Go-SQLBuilder6.2 Gendry6.3 自行实现SQLBuilder7. GORM8. Go操作MongoDB1. SQL语法简介 SQL(Structured Query Language)是一套语法标准&#…...

【颠覆软件开发】华为自研IDE!未来IDE将不可预测!
IDE是软件开发生态的入口,但目前我们所使用的IDE基本都是由国外巨头提供,比如Visual Studio、Eclipse、JetBrains。这些IDE具有很高的断供风险,与操作系统、芯片、编程语言一样,非常重要。 随着越来越多的软件开始采用云上开发模…...

怎样从零基础学黑客
可以说想学黑客技术,要求你首先是一个“T”字型人才,也就是说电脑的所有领域你都能做的来,而且有一项是精通的。因此作为一个零基础的黑客爱好者来说,没有良好的基础是绝对不行的,下面我就针对想真正学习黑客的零基础朋…...
burp小程序抓包
身为一名码农,抓包肯定是一项必备技能。工作中遇到很多次需要对小程序进行抓包排查问题。下面分享一下我的抓包方式,使用的是电脑版小程序抓包,跟手机的方式都差不多的。 一、环境 微信版本:3.6.0.18 Burpsuite版本:…...

文件上传攻击骚操作
允许直接上传shell 只要有文件上传功能,那么就可以尝试上传webshell直接执行恶意代码,获得服务器权限,这是最简单也是最直接的利用。 允许上传压缩包 如果可以上传压缩包,并且服务端会对压缩包解压,那么就可能存在Zip …...
Scala流程控制(第四章:分支控制、嵌套分支、switch分支、for循环控制全、while与do~while、多重与中断)
文章目录第 4 章 流程控制4.1 分支控制 if-else4.1.1 单分支4.1.2 双分支4.1.3 多分支4.2 嵌套分支4.3 Switch 分支结构4.4 For 循环控制4.4.1 范围数据循环(To)4.4.2 范围数据循环(Until)4.4.3 循环守卫4.4.4 循环步长4.4.5 嵌套…...
)
华为OD机试真题Python实现【整理扑克牌】真题+解题思路+代码(20222023)
整理扑克牌 题目 给定一组数字,表示扑克牌的牌面数字,忽略扑克牌的花色,请安如下规则对这一组扑克牌进行整理。 步骤一: 对扑克牌进行分组,规则如下 当牌面数字相同张数大于等于4时,组合牌为炸弹;三张相同牌面数字+两张相同牌面数字,且三张牌与两张牌不相同时,组合牌…...
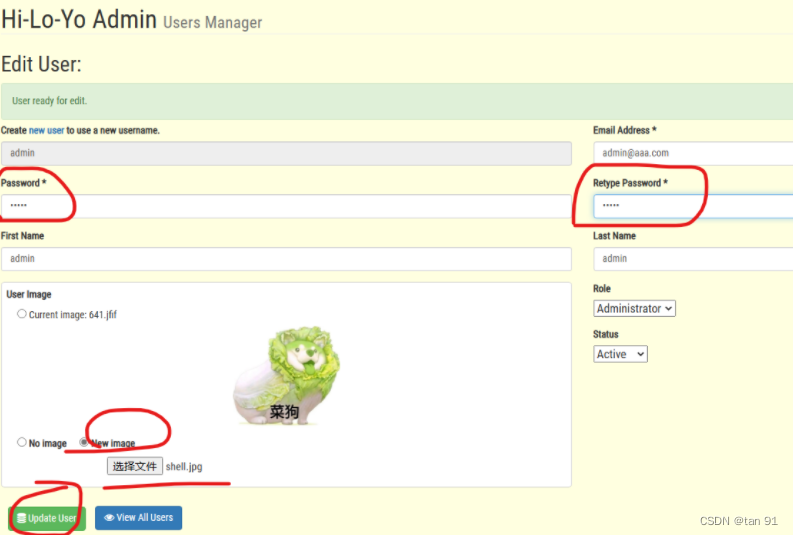
【春秋云境】CVE-2022-28525
靶标介绍: ED01-CMS v20180505 存在任意文件上传漏洞 打开靶场: 盲猜一波弱密码admin:admin就进去了。登录后在图中位置点击进行图片更新,需要将密码等都写上 抓包将图片信息进行替换,并修改文件名: POST /admin…...

Android设置取消系统闹钟
系统闹钟包名:com.android.deskclock 调用系统闹钟,首先在清单文件AndroidManifest.xml中添加权限: <uses-permission android:name"com.android.alarm.permission.SET_ALARM" />设置系统闹钟: public static v…...

使用 Node.js 多进程提高任务执行效率
什么是 Node 多进程? Node 是在单个线程中运行,我们虽然没办法开启额外的线程,但是可以开启进程集群。这样可以让下载任务和上传任务同时进行。 使用多进程进行初步代码优化 const dl require(./download.js) const ul require(./upload…...
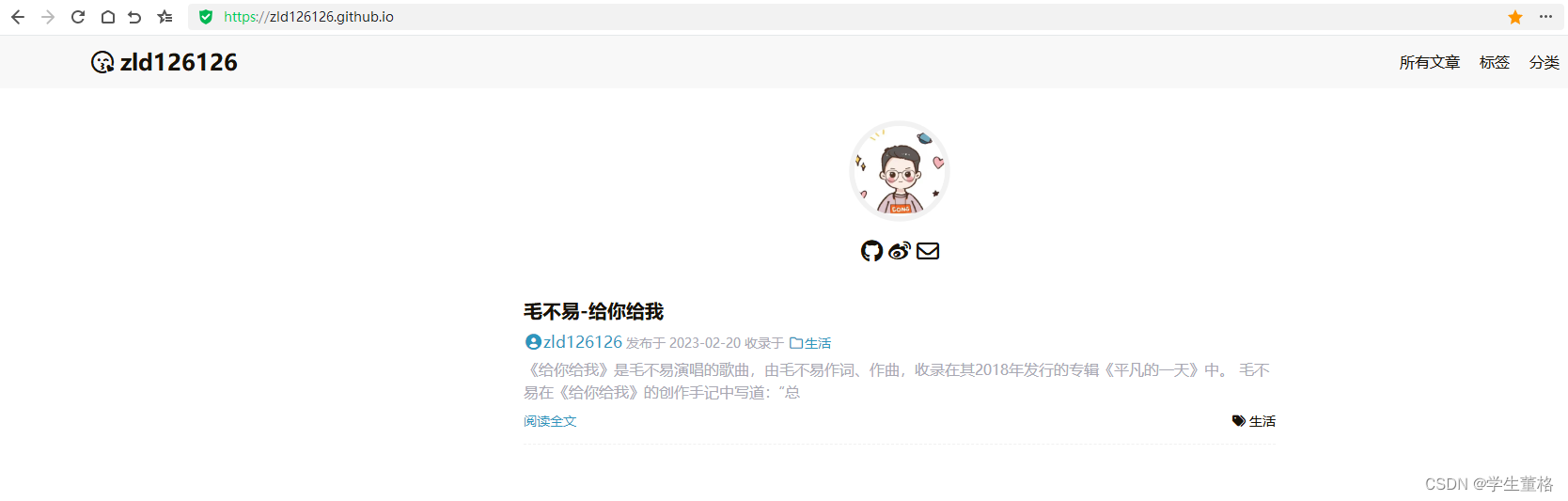
[Golang实战]github.io部署个人博客hugo[新手开箱可用][小白教程]
[Golang实战]github.io部署个人博客hugo[新手开箱可用][小白教程]1.新手教程(小白也能学会)2.开始准备2.1myBlog是hugo的项目1.安装Hugo2.创建hugo项目2.2 xxxx.github.io是github.io中规定的pages项目3.成功部署4.TODO自动化workflows部署github.io1.新手教程(小白也能学会) …...

50个 Pandas 高频操作技巧,建议收藏
在数据分析和数据建模的过程中需要对数据进行清洗和整理等工作,有时需要对数据增删字段。 下面为大家介绍Pandas对数据的复杂查询、数据类型转换、数据排序、数据的修改、数据迭代以及函数的使用 文章目录技术交流01、复杂查询1、逻辑运算2、逻辑筛选数据3、函数筛…...

pygraphviz安装教程
0x01. 背景 最近在做casual inference,做实验时候想因果图可视化,遂需要安装pygraphviz,整了一下午,终于捣鼓好了,真头大。 环境: win10操作系统python3.9环境 0x02. 安装Graphviz 传送门:…...
HarmonyOS Connect认证测试
在HarmonyOS Connect生态产品的认证测试过程中,你是否存在这些疑问:认证流程具体包括哪些操作环节?如何根据实际场景选择合适的认证方式?如何选择认证测试标准的版本…… 本期FAQ为大家带来HarmonyOS Connect认证测试的常见问题…...

Datawhale团队第九期录取名单!
Datawhale团队 公示:Datawhale团队成员Datawhale成立四年了,从一开始的12个人,学习互助,到提议成立开源组织,做更多开源的事情,帮助更多学习者,也促使我们更好地成长。于是有了我们的使命&#…...

ChatGPT 的原理与未来研究方向
1、原理: 架构:chatGPT是一种基于转移学习的大型语言模型,它使用GPT-3.2 (Generative PretrainedTransformer2)模型的技术,使用了transformer的架构,并进行了进一步的训练和优化。InstructGPT/…...

基于UIAutomation+Python+Unittest+Beautifulreport的WindowsGUI自动化测试框架主入口main解析
文章目录1 main.py主入口2 testcase目录2.1 实例:test\_test\_mymusic.py2.2 实例:test\_toolbar.py3 page目录3.1 page/mymusic.py3.2 page/toolbar.py注: 1、本文为本站首发,他用请联系作者并注明出处,谢谢ÿ…...
)
华为OD机试真题Python实现【挑选字符串】真题+解题思路+代码(20222023)
挑选字符串 题目 给定a-z,26 个英文字母小写字符串组成的字符串A和B, 其中A可能存在重复字母,B不会存在重复字母, 现从字符串A中按规则挑选一些字母可以组成字符串B 挑选规则如下: 同一个位置的字母只能挑选一次, 被挑选字母的相对先后顺序不能被改变, 求最多可以同时…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

