AcWing 482. 合唱队形
482. 合唱队形
N 位同学站成一排,音乐老师要请其中的 (N−K) 位同学出列,使得剩下的 K 位同学排成合唱队形。
合唱队形是指这样的一种队形:设 K位同学从左到右依次编号为 1,2…,K,他们的身高分别为 T1,T2,…,TK, 则他们的身高满足 T1<…<Ti>Ti+1>…>TK(1≤i≤K)。
你的任务是,已知所有 N 位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。
输入格式
输入的第一行是一个整数 N,表示同学的总数。
第二行有 N 个整数,用空格分隔,第 i 个整数 Ti是第 i 位同学的身高(厘米)。
输出格式
输出包括一行,这一行只包含一个整数,就是最少需要几位同学出列。
数据范围
2≤N≤100
130≤Ti≤230
输入样例:
8
186 186 150 200 160 130 197 220输出样例:
4假设最优解的中心是第 i 个人,则 T1,T2,…,Ti 一定是以 Ti 结尾的最长上升子序列。同理,TK,TK−1,…,Ti也一定是以 Ti 结尾的最长上升子序列。因此可以先预处理出:
从前往后以每个点结尾的最长上升子序列长度 f[i];
从后往前以每个点结尾的最长上升子序列长度 g[i];
那么以 k 为中心的最大长度就是 f[k] + g[k] - 1,遍历 k = 1, 2, ..., n 取最大值即为答案。
求最长上升子序列问题(LIS)可以参考 AcWing 895. 最长上升子序列。
时间复杂度
本题数据范围只有 100,因此可以用朴素的LIS求解方式,时间复杂度是 O(n2),使用贪心 + 二分可以将时间复杂度优化到 O(nlogn),具体可以参考 AcWing 896. 最长上升子序列 II。
AC代码如下:
#include <bits/stdc++.h>
using namespace std;int n;
int bxj[101];//以第i位同学为终点的最长不下降序列的长度
int bss[101];//以第i位同学为起点的最长不上升序列的长度
int t[101];int main()
{int maxn = 0;scanf("%d", &n);for(int i = 1; i <= n; i++){scanf("%d", &t[i]);}
// memset(bss, 1, sizeof(bss));
// memset(bxj, 1, sizeof(bxj));bxj[1] = 1;bss[n] = 1;for(int i = 1; i <= n; i++){maxn = 0;for(int j = 1; j < i; j++){if(t[i] > t[j])if(bxj[j] > maxn)maxn = bxj[j]; }bxj[i] = maxn + 1;}for(int i = n - 1; i >= 1; i--){maxn = 0;for(int j = i + 1; j <= n; j++){if(t[i] > t[j])if(bss[j] > maxn)maxn = bss[j];}bss[i] = maxn + 1;}maxn = 0;for(int i = 1; i <= n; i++){if((bxj[i] + bss[i]) > maxn)maxn = bxj[i] + bss[i];}cout << n - maxn + 1 << endl;
// for(int i = 1; i <= n; i++)
// {
// cout << i << " " ;
// }
// cout << endl;
// for(int i = 1; i <= n; i++)
// {
// cout << bxj[i] << " " ;
// }
// cout << endl;
// for(int i = 1; i <= n; i++)
// {
// cout << bss[i] << " " ;
// }return 0;
}相关文章:

AcWing 482. 合唱队形
482. 合唱队形N 位同学站成一排,音乐老师要请其中的 (N−K) 位同学出列,使得剩下的 K 位同学排成合唱队形。 合唱队形是指这样的一种队形:设 K位同学从左到右依次编号为 1,2…,K,他们的身高分别为…...
Pytorch深度学习实战3-4:通俗理解张量Tensor的爱因斯坦求和(附实例)
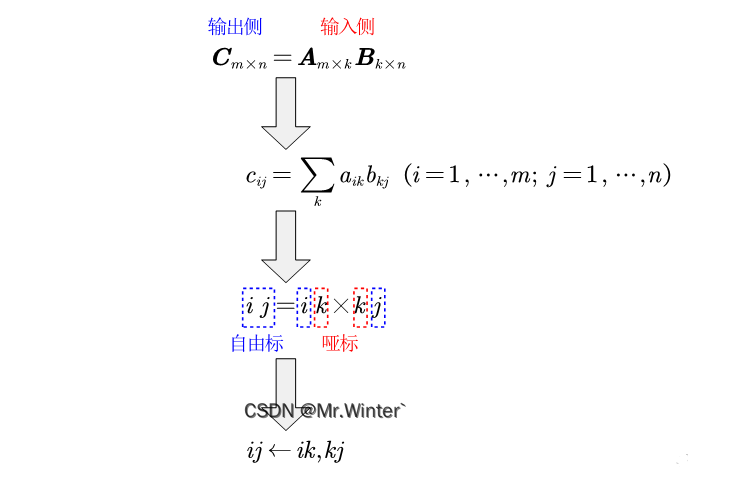
目录1 爱因斯坦求和由来2 爱因斯坦求和原理3 实例:字母表示法3.1 向量运算3.2 矩阵运算3.3 张量运算4 实例:常量表示法4.1 向量运算4.2 矩阵运算4.3 张量运算1 爱因斯坦求和由来 爱因斯坦求和约定(Einstein summation convention)是一种标记的约定&#…...
GEE学习笔记 五十六:GEE中如何把文件导出到Google Drive的子目录
今天在群里看到有人在问一个问题,如何使用GEE把文件导出到Google Drive的子目录中?这里我就简单的说一下这个问题。 首先,在GEE中我们都知道了如何将数据导出导出Google Drive的文件夹中,如下面的一个例子: var geome…...

【Go基础】数据库编程
文章目录1. SQL语法简介2. MySQL最佳实践3. Go SQL驱动接口解读4. 数据库增删改查5. stmt6. SQLBuilder6.1 Go-SQLBuilder6.2 Gendry6.3 自行实现SQLBuilder7. GORM8. Go操作MongoDB1. SQL语法简介 SQL(Structured Query Language)是一套语法标准&#…...

【颠覆软件开发】华为自研IDE!未来IDE将不可预测!
IDE是软件开发生态的入口,但目前我们所使用的IDE基本都是由国外巨头提供,比如Visual Studio、Eclipse、JetBrains。这些IDE具有很高的断供风险,与操作系统、芯片、编程语言一样,非常重要。 随着越来越多的软件开始采用云上开发模…...

怎样从零基础学黑客
可以说想学黑客技术,要求你首先是一个“T”字型人才,也就是说电脑的所有领域你都能做的来,而且有一项是精通的。因此作为一个零基础的黑客爱好者来说,没有良好的基础是绝对不行的,下面我就针对想真正学习黑客的零基础朋…...
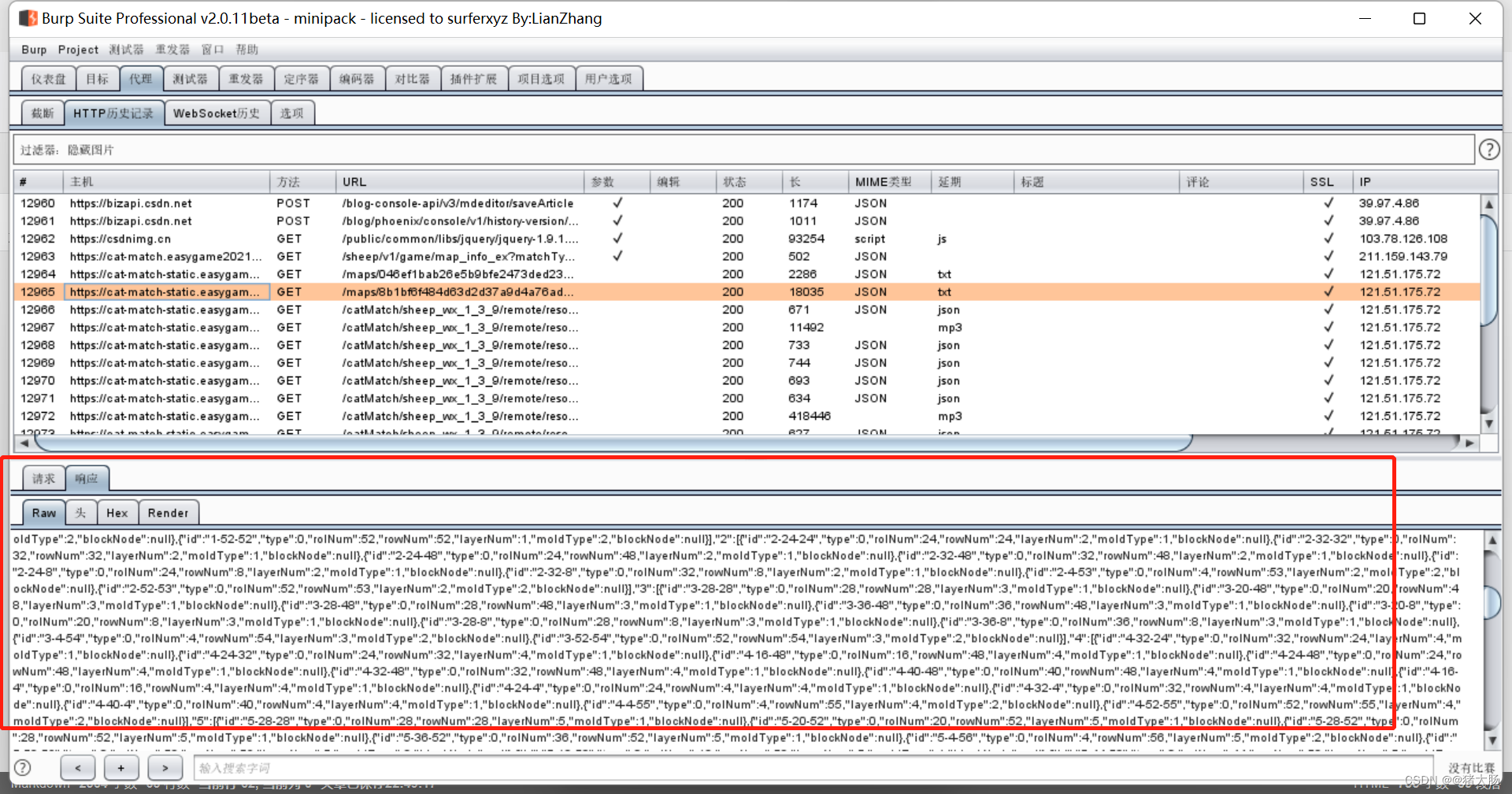
burp小程序抓包
身为一名码农,抓包肯定是一项必备技能。工作中遇到很多次需要对小程序进行抓包排查问题。下面分享一下我的抓包方式,使用的是电脑版小程序抓包,跟手机的方式都差不多的。 一、环境 微信版本:3.6.0.18 Burpsuite版本:…...

文件上传攻击骚操作
允许直接上传shell 只要有文件上传功能,那么就可以尝试上传webshell直接执行恶意代码,获得服务器权限,这是最简单也是最直接的利用。 允许上传压缩包 如果可以上传压缩包,并且服务端会对压缩包解压,那么就可能存在Zip …...
Scala流程控制(第四章:分支控制、嵌套分支、switch分支、for循环控制全、while与do~while、多重与中断)
文章目录第 4 章 流程控制4.1 分支控制 if-else4.1.1 单分支4.1.2 双分支4.1.3 多分支4.2 嵌套分支4.3 Switch 分支结构4.4 For 循环控制4.4.1 范围数据循环(To)4.4.2 范围数据循环(Until)4.4.3 循环守卫4.4.4 循环步长4.4.5 嵌套…...
)
华为OD机试真题Python实现【整理扑克牌】真题+解题思路+代码(20222023)
整理扑克牌 题目 给定一组数字,表示扑克牌的牌面数字,忽略扑克牌的花色,请安如下规则对这一组扑克牌进行整理。 步骤一: 对扑克牌进行分组,规则如下 当牌面数字相同张数大于等于4时,组合牌为炸弹;三张相同牌面数字+两张相同牌面数字,且三张牌与两张牌不相同时,组合牌…...
【春秋云境】CVE-2022-28525
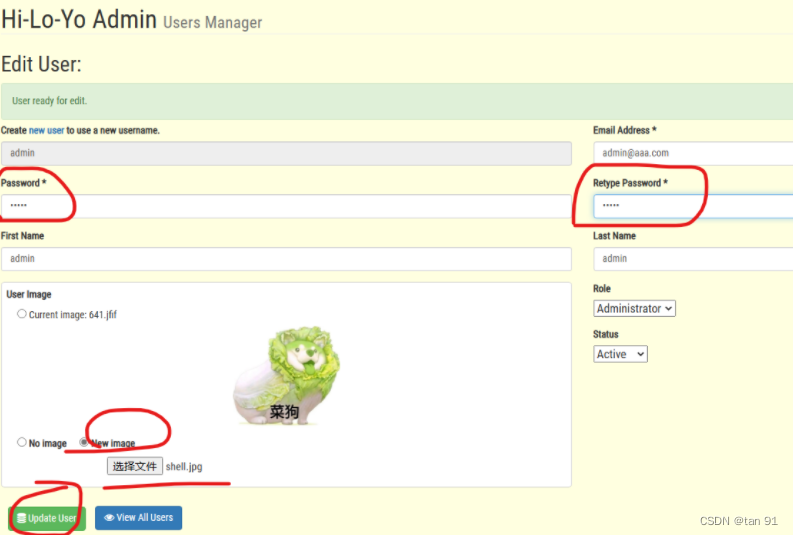
靶标介绍: ED01-CMS v20180505 存在任意文件上传漏洞 打开靶场: 盲猜一波弱密码admin:admin就进去了。登录后在图中位置点击进行图片更新,需要将密码等都写上 抓包将图片信息进行替换,并修改文件名: POST /admin…...

Android设置取消系统闹钟
系统闹钟包名:com.android.deskclock 调用系统闹钟,首先在清单文件AndroidManifest.xml中添加权限: <uses-permission android:name"com.android.alarm.permission.SET_ALARM" />设置系统闹钟: public static v…...

使用 Node.js 多进程提高任务执行效率
什么是 Node 多进程? Node 是在单个线程中运行,我们虽然没办法开启额外的线程,但是可以开启进程集群。这样可以让下载任务和上传任务同时进行。 使用多进程进行初步代码优化 const dl require(./download.js) const ul require(./upload…...
[Golang实战]github.io部署个人博客hugo[新手开箱可用][小白教程]
[Golang实战]github.io部署个人博客hugo[新手开箱可用][小白教程]1.新手教程(小白也能学会)2.开始准备2.1myBlog是hugo的项目1.安装Hugo2.创建hugo项目2.2 xxxx.github.io是github.io中规定的pages项目3.成功部署4.TODO自动化workflows部署github.io1.新手教程(小白也能学会) …...

50个 Pandas 高频操作技巧,建议收藏
在数据分析和数据建模的过程中需要对数据进行清洗和整理等工作,有时需要对数据增删字段。 下面为大家介绍Pandas对数据的复杂查询、数据类型转换、数据排序、数据的修改、数据迭代以及函数的使用 文章目录技术交流01、复杂查询1、逻辑运算2、逻辑筛选数据3、函数筛…...

pygraphviz安装教程
0x01. 背景 最近在做casual inference,做实验时候想因果图可视化,遂需要安装pygraphviz,整了一下午,终于捣鼓好了,真头大。 环境: win10操作系统python3.9环境 0x02. 安装Graphviz 传送门:…...
HarmonyOS Connect认证测试
在HarmonyOS Connect生态产品的认证测试过程中,你是否存在这些疑问:认证流程具体包括哪些操作环节?如何根据实际场景选择合适的认证方式?如何选择认证测试标准的版本…… 本期FAQ为大家带来HarmonyOS Connect认证测试的常见问题…...

Datawhale团队第九期录取名单!
Datawhale团队 公示:Datawhale团队成员Datawhale成立四年了,从一开始的12个人,学习互助,到提议成立开源组织,做更多开源的事情,帮助更多学习者,也促使我们更好地成长。于是有了我们的使命&#…...

ChatGPT 的原理与未来研究方向
1、原理: 架构:chatGPT是一种基于转移学习的大型语言模型,它使用GPT-3.2 (Generative PretrainedTransformer2)模型的技术,使用了transformer的架构,并进行了进一步的训练和优化。InstructGPT/…...

基于UIAutomation+Python+Unittest+Beautifulreport的WindowsGUI自动化测试框架主入口main解析
文章目录1 main.py主入口2 testcase目录2.1 实例:test\_test\_mymusic.py2.2 实例:test\_toolbar.py3 page目录3.1 page/mymusic.py3.2 page/toolbar.py注: 1、本文为本站首发,他用请联系作者并注明出处,谢谢ÿ…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...
