数据结构和算法(2):向量
抽象数据类型

数组到向量
C/C++ 中,数组A[]中的元素与[0,n)内的编号一一对应,A[0],A[1],...,A[n-1];反之,每个元素均由(非负)编号唯一指代,并可直接访问A[i] 的物理地址 = A+i × s,s 为单个元素占用的空间量,所以也叫作线性数组。
向量是数组的抽象与泛化,由一组元素按线性次数封装而成。各元素与[0,n)内的秩(rank)一一对应。
元素的类型不限于基本类型;
操作、管理维护更加简化、统一与安全;
可更为便捷地参与复杂数据结构的定制与实现

Vector 模板类
using Rank = unsigned int; //秩
#define DEFAULT_CAPACITY 3 //默认的初始容量(实际应用中可设置为更大)
template <typename T> class Vector { //向量模板类
private:Rank_size;int_capacity;T* _elem;//规模、容量、数据区
protected:/.../
public://构造函数Vector ( Rank c = DEFAULT_CAPACITY, Rank s = 0, T v = 0 ) //容量为c、规模为s、所有元素初始为v{ _elem = new T[_capacity = c]; for ( _size = 0; _size < s; _elem[_size++] = v ); } //s<=cVector ( T const* A, Rank n ) { copyFrom ( A, 0, n ); } //数组整体复制Vector ( T const* A, Rank lo, Rank hi ) { copyFrom ( A, lo, hi ); } //区间Vector ( Vector<T> const& V ) { copyFrom ( V._elem, 0, V._size ); } //向量整体复制Vector ( Vector<T> const& V, Rank lo, Rank hi ) { copyFrom ( V._elem, lo, hi ); } //区间// 析构函数~Vector() { delete [] _elem; } //释放内部空间
}; //Vector
可扩充向量
静态空间管理
开辟内部数组_elem[]并使用一段地址连续的物理空间
_capacity :总容量
_size:当前的实际规模n
若采用静态空间管理策略,容量_capacity固定,则有明显的不足
1.上溢( overf1ow ) : _elem[]不足以存放所有元素
尽管此时系统仍有足够的空间
2.下溢( underflow ) : _elem[]中的元素寥寥无几
装填因子(load factor) λ = _ s i z e / _ c a p a c i t y < < 50 % \lambda = \_size/\_capacity << 50\% λ=_size/_capacity<<50%
更糟糕的是,一般的应用环境中难以准确预测空间的需求量。
动态空间管理
在即将发生上溢时,适当地扩大内部数组的容量
template <typename T>
void Vector<T>::expand() { //向量空间不足时扩容if(_size < _capacity) return; //尚未满员时,不必扩容_capacity = max(_capacity, DEFAULT_CAPACITY); //不低于最小容量T* oldElem =_elem; _elem = new T[_capacity <<= 1];//容量加倍for (int i = 0; i <_size; i++) //复制原向量内容_elem[i] = oldElem[i]; //T为基本类型,或已重载赋值操作符'='delete [] oldElem; //释放原空间
}
得益于向量的封装,尽管扩容之后数据区的物理地址有所改变,却不致出现野指针。
容量加倍策略在时间复杂度上总体优于容量递增策略。
| \space | 递增策略 | 倍增策略 |
|---|---|---|
| 累计增容时间 | O ( n 2 ) \mathcal O(n^2) O(n2) | O ( n ) \mathcal O(n) O(n) |
| 分摊增容时间 | O ( n ) \mathcal O(n) O(n) | O ( 1 ) \mathcal O(1) O(1) |
| 装填因子 | ≈ 100 % ≈100\% ≈100% | > 50 % >50\% >50% |
平均分析 vs 分摊分析
平均复杂度或期望复杂度(average/expected complexity)
根据数据结构各种操作出现概率的分布,将对应的成本加权平均
各种可能的操作,作为独立事件分别考查
割裂了操作之间的相关性和连贯性
往往不能准确地评判数据结构和算法的真实性能
分摊复杂度(amortized complexity)
对数据结构连续地实施足够多次操作,所需总体成本分摊至单次操作
从实际可行的角度,对一系列操作做整体的考量
更加忠实地刻画了可能出现的操作序列
可以更为精准地评判数据结构和算法的真实性能
分摊复杂度和平均复杂度的结果并没有必然联系。
无序向量
元素访问
通过V.get(r)和V.put(r)接口,可以对元素进行读写。
可以重载下标操作符,增加其便捷性:
template<typename T> //0 <= _size
T & Vector<T>::operator[](Rank(r)) const {return _elem[r];}
此后,对外的V[r]即对应内部的V._elem[r]可以使用下标进行操作:
//右值
T x = V[r] + U[s] + W[t];
//左值
V[r] = T(2*x + 3);
插入
template <typename T> //将e插入至[r]
Rank Vector<T>::insert ( Rank r, T const& e ) { //0 <= r <= sizeexpand(); //如必要,先扩容for ( Rank i = _size; r < i; i-- ) //自后向前,后继元素_elem[i] = _elem[i-1]; //顺次后移一个单元_elem[r] = e; _size++; //置入新元素并更新容量return r; //返回秩
}
区间删除
template <typename T> int Vector<T>::remove( Rank lo, Rank hi ) { //0 <= lo <= hi <= nif ( lo == hi ) return 0; //出于效率考虑,单独处理退化情况while ( hi < _size ) _elem[lo++] = _elem[hi++]; //后缀[hi, _size)顺次前移 hi-lo 位_size = lo; shrink(); //更新规模,lo=_size之后的内容无需清零;如必要,则缩容//若有必要,则缩容return hi-lo;//返回被删除元素的数目
}
单元素删除
可以视作区间删除的特例:[r] = [r,r+1)
template <typename T> T Vector<T>::remove( Rank r ) { //删除向量中秩为r的元素,0 <= r < sizeT e = _elem[r]; //备份被删除元素remove( r, r + 1 ); //调用区间删除算法,等效于对区间[r, r + 1)的删除return e; //返回被删除元素
}
查找
template <typename T> //在无序向量中顺序查找e:成功则返回最靠后的出现位置,否则返回lo-1
Rank Vector<T>::find ( T const& e, Rank lo, Rank hi ) const { //0 <= lo < hi <= _sizewhile ( ( lo < hi-- ) && ( e != _elem[hi] ) ); //从后向前,顺序查找return hi; //若hi < lo,则意味着失败;否则hi即命中元素的秩
}
输入敏感:最好: O ( 1 ) \mathcal O(1) O(1) ; 最差: O ( n ) \mathcal O(n) O(n)
实例:去重(删除重复元素)
template <typename T> Rank Vector<T>::dedup() { //删除无序向量中重复元素(高效版)Rank oldSize = _size; //记录原规模for ( Rank i = 1; i < _size; ) //自前向后逐个考查_elem[1,_size)if ( -1 == find(_elem[i], 0, i) ) //在前缀[0,i)中寻找与[i]雷同者(至多一个),O(i)i++; //若无雷同,则继续考查其后继elseremove(i); //否则删除[i],O(_size-i)return oldSize - _size; //被删除元素总数
}
每轮迭代中 find() 和 remove(累计耗费线性时间,总体为 O ( n 2 ) \mathcal O(n^2) O(n2) )
有序向量:唯一化
有序/无序序列中,任意/总有一对相邻元素顺序/逆序因此,相邻逆序对的数目,可用以度量向量的逆序程度。
实例:有序向量去重
观察︰在有序向量中,重复的元素必然相互紧邻构成一个区间。因此,每一区间只需保留单个元素即可
低效算法
template <typename T> Rank Vector<T>::uniquify() { //有序向量重复元素剔除算法(低效版)Rank oldSize = _size, i = 1; //当前比对元素的秩,起始于首元素while ( i < _size ) //从前向后,逐一比对各对相邻元素_elem[i - 1] == _elem[i] ? remove ( i ) : i++; //若雷同,则删除后者;否则,转至后一元素return oldSize - _size; //向量规模变化量,即被删除元素总数
}
效率低,运行时间主要取决于 while 循环,次数共计:_size - 1 = n -1
最坏: O ( n 2 ) \mathcal O(n^2) O(n2)
高效算法
反思:低效的根源狂于,同一元素可作为被删除元素的后继多次前移
启示︰若能以重复区间为单位,成批删除雷同元素,性能必将改进
template <typename T> Rank Vector<T>::uniquify() { //有序向量重复元素剔除算法(高效版)Rank i = 0, j = 0; //各对互异“相邻”元素的秩while ( ++j < _size ) //逐一扫描,直至末元素if ( _elem[i] != _elem[j] ) //跳过雷同者_elem[++i] = _elem[j]; //发现不同元素时,向前移至紧邻于前者右侧_size = ++i; shrink(); //直接截除尾部多余元素return j - i; //向量规模变化量,即被删除元素总数
}
共计 n - 1 次迭代,每次常数时间,累计 O ( n ) \mathcal O(n) O(n) 时间。
有序向量:二分查找(A)
//二分查找算法(版本A)︰在有序向量的区间[lo,hi)内查找元素e,0 <= lo <= hi <= _size
template <typename T> static Rank binSearch( T* S, T const& e, Rank lo,Rank hi ) {while ( lo < hi ) { //每步迭代可能要做两次比较判断,有三个分支Rank mi = ( lo + hi ) >>1; //以中点为轴点(区间宽度折半,等效于其数值表示的右移一位)if( e < s[mi] ) hi = mi; //深入前半 段[ 1o, mi)继续查找else if ( S[mi] < e ) lo = mi + 1; //深入后半段(mi,hi)继续查找elsereturn mi; //在mi处命中} //成功查找可以提前终止return -1; //查找失败
} //有多个命中元素时,不能保证返回秩最大者;查找失败时,简单地返回-1,而不能指示失败的位置
转向左、右分支前的关键码比较次数不等,而递归深度却相同
有序向量:Fib 查找
若能通过递归深度的不均衡,对转向成本的不均衡进行补偿平均查找长度应能进一步缩短…
#include "fibonacci/Fib.h" //引入Fib数列类
//Fibonacci查找算法(版本A):在有序向量的区间[lo, hi)内查找元素e,0 <= lo <= hi <= _size
template <typename T> static Rank fibSearch( T* S, T const& e, Rank lo, Rank hi ) {//用O(log_phi(n = hi - lo)时间创建Fib数列for ( Fib fib( hi - lo ); lo < hi; ) { //Fib制表备查;此后每步迭代仅一次比较、两个分支while ( hi - lo < fib.get() ) fib.prev(); //自后向前顺序查找(分摊O(1))Rank mi = lo + fib.get() - 1; //确定形如Fib(k)-1的轴点if ( e < S[mi] ) hi = mi; //深入前半段[lo, mi)继续查找else if ( S[mi] < e ) lo = mi + 1; //深入后半段(mi, hi)继续查找else return mi; //在mi处命中} //一旦找到,随即终止return -1; //查找失败
} //有多个命中元素时,不能保证返回秩最大者;失败时,简单地返回-1,而不能指示失败的位置
通用策略:对于任何的 A [ 0 , n ) A[0,n) A[0,n),总是选取 A [ λ n ] A[\lambda n] A[λn] 作为轴点, 0 ≤ λ < 1 0\leq \lambda<1 0≤λ<1
在 [ 0 , 1 ) [0,1) [0,1)内, λ \lambda λ 如何取值才能达到最优 ? 设平均查找长度为 α ( λ ) ⋅ l o g 2 n α(\lambda)· log_2n α(λ)⋅log2n,何时 α ( λ ) α(\lambda) α(λ) 最小?
二分查找: λ = 0.5 \lambda = 0.5 λ=0.5 Fib 查找: 0.6180339... 0.6180339... 0.6180339...
有序向量:二分查找(B)
二分查找中左、右分支转向代价不平衡的问题,也可直接解决。将中间点包含在了右边。
//二分查找算法(版本B):在有序向量的区间[lo, hi)内查找元素e,0 <= lo < hi <= _size
template <typename T> static Rank binSearch( T* S, T const& e, Rank lo, Rank hi ) {while ( 1 < hi - lo ) { //每步迭代仅需做一次比较判断,有两个分支;成功查找不能提前终止Rank mi = ( lo + hi ) >> 1; //以中点为轴点(区间宽度折半,等效于其数值表示的右移一位)( e < S[mi] ) ? hi = mi : lo = mi; //经比较后确定深入[lo, mi)或[mi, hi)} //出口时hi = lo + 1,查找区间仅含一个元素A[lo]return e < S[lo] ? lo - 1 : lo; //返回位置,总是不超过e的最大者
} //有多个命中元素时,返回秩最大者;查找失败时,简单地返回-1,而不能指示失败的位置
有序向量:二分查找(C)
//二分查找算法(版本C):在有序向量的区间[lo, hi)内查找元素e,0 <= lo <= hi <= _size
template <typename T> static Rank binSearch( T* S, T const& e, Rank lo, Rank hi ) {while ( lo < hi ) { //每步迭代仅需做一次比较判断,有两个分支Rank mi = ( lo + hi ) >> 1; //以中点为轴点(区间宽度折半,等效于其数值表示的右移一位)( e < S[mi] ) ? hi = mi : lo = mi + 1; //经比较后确定深入[lo, mi)或(mi, hi)} //成功查找不能提前终止return lo - 1; //至此,[lo]为大于e的最小者,故[lo-1]即为不大于e的最大者
} //有多个命中元素时,返回最靠后者;查找失败时,返回失败的位置
与版本B的差异
1)待查找区间宽度缩短至e而非1时,算法才结束
2)转入右侧子向量时,左边界取作mi + 1而非mi——A[mi]会被遗漏?
3)无论成功与否,返回的秩严格符合接口的语义约定…
冒泡排序
向量元素若有序排列,计算效率将大大提升
template <typename T> void vector<T>::bubbleSort(Rank lo,Rank h1)
{ while (!bubble(lo,hi--)); } //逐趟做扫描交换,直至全序template <typename T> bool Vector<T>::bubble(Rank lo,Rank hi) {bool sorted = true; //整体有序标志while (++lo < hi) //自左向右,逐一检查各对相邻元素if (_elem[lo - 1] > _elem[lo]) { //若逆序,则sorted = false;//意味着尚未整体有序,并需要swap(_elem[lo - 1],_elem[lo]);//交换}return sorted; l/返回有序标志
}//乱序限于[0,√n)时,仍需O(n^{3/2})时间——按理,O(n)应已足矣
改进:
template <typename T> void vector<1>::bubbleSort(Rank lo,Rank h1)
{ while (lo < (hi = bubble(lo,hi)));}//逐趟扫描交换,直至全序
template <typename T> Rank Vector<T> : :bubble(Rank lo,Rank hi) {Rank last = lo;//最右侧的逆序对初始化为[lo - 1,1o]while (++lo < hi)//自左向右,逐一检查各对相邻元素if(_elem[lo - 1] > _elem[lo])//若逆序,则last = lo;//更新最右侧逆序对位置记录,并swap(_elem[lo - 1],_elem[lo]);//交换}return last;//返回最右侧的逆序对位置
}//前一版本中的逻辑型标志sorted,改为秩last
三种冒泡排序算法效率相同,最好o(n),最坏o(n^2)
在冒泡排序中,元素 a 和 b 的相对位置发生变化,只有一种可能;
1.经分别与其它元素的交换,二者相互接近直至相邻
2.在接下来一轮扫描交换中,二者因逆序而交换位置
归并排序
分治策略,向量与列表通用
序列一分为二 ( O ( 1 ) ) (\mathcal O(1)) (O(1)),子序列递归排序 ( 2 × T ( n / 2 ) ) (2 \times T(n/2)) (2×T(n/2)),合并有序子序列 ( O ( n ) ) (\mathcal O(n)) (O(n))
总体复杂度为 ( O ( n log n ) ) (\mathcal O(n\log n)) (O(nlogn))
template <typename T> //向量归并排序
void Vector<T>::mergeSort( Rank lo, Rank hi ) { // 0 <= lo < hi <= sizeif ( hi - lo < 2 ) return; //单元素区间自然有序,否则...Rank mi = ( lo + hi ) / 2; //以中点为界mergeSort( lo, mi ); mergeSort( mi, hi ); //前缀、后缀分别排序merge( lo, mi, hi ); //归并
}template <typename T> //对各自有序的[lo, mi)和[mi, hi)做归并
void Vector<T>::merge( Rank lo, Rank mi, Rank hi ) { // lo < mi < hiRank i = 0; T* A = _elem + lo; //合并后的有序向量A[0, hi - lo) = _elem[lo, hi)Rank j = 0, lb = mi - lo; T* B = new T[lb]; //前子向量B[0, lb) <-- _elem[lo, mi)for ( Rank i = 0; i < lb; i++ ) B[i] = A[i]; //复制出A的前缀Rank k = 0, lc = hi - mi; T* C = _elem + mi; //后缀C[0, lc) = _elem[mi, hi)就地while ( ( j < lb ) && ( k < lc ) ) //反复地比较B、C的首元素A[i++] = ( B[j] <= C[k] ) ? B[j++] : C[k++]; //将更小者归入A中while ( j < lb ) //若C先耗尽,则A[i++] = B[j++]; //将B残余的后缀归入A中——若B先耗尽呢?delete[] B; //释放临时空间:mergeSort()过程中,如何避免此类反复的new/delete?
}
算法的运行时间主要在于 for 循环,merge() 总体迭代不超过 O ( n ) \mathcal O(n) O(n) 次,累计只需线性时间。 T ( n ) = 2 T ( n / 2 ) + O ( n ) T(n) = 2T(n/2)+\mathcal O(n) T(n)=2T(n/2)+O(n)
位图
位图(Bitmap)是一种数据结构,用于表示一组位或二进制值的集合。在计算机科学中,位图通常用于存储和操作大量的二进制数据,其中每个位都表示某种状态或信息。
位图中的每个位(或者可以理解为数组的元素)代表一个元素是否存在于集合中。当元素存在时,对应位的值为1;不存在时,对应位的值为0。
相关文章:

数据结构和算法(2):向量
抽象数据类型 数组到向量 C/C 中,数组A[]中的元素与[0,n)内的编号一一对应,A[0],A[1],...,A[n-1];反之,每个元素均由(非负)编号唯一指代,并可直接访问A[i] 的物理地址 Ai s,s 为单…...

mysql 大表如何ddl
大家好,我是蓝胖子,mysql对大表(千万级数据)的ddl语句,在生产上执行时一定要千万小心,一不小心就有可能造成业务阻塞,数据库io和cpu飙高的情况。今天我们就来看看如何针对大表执行ddl语句。 通过这篇文章,…...
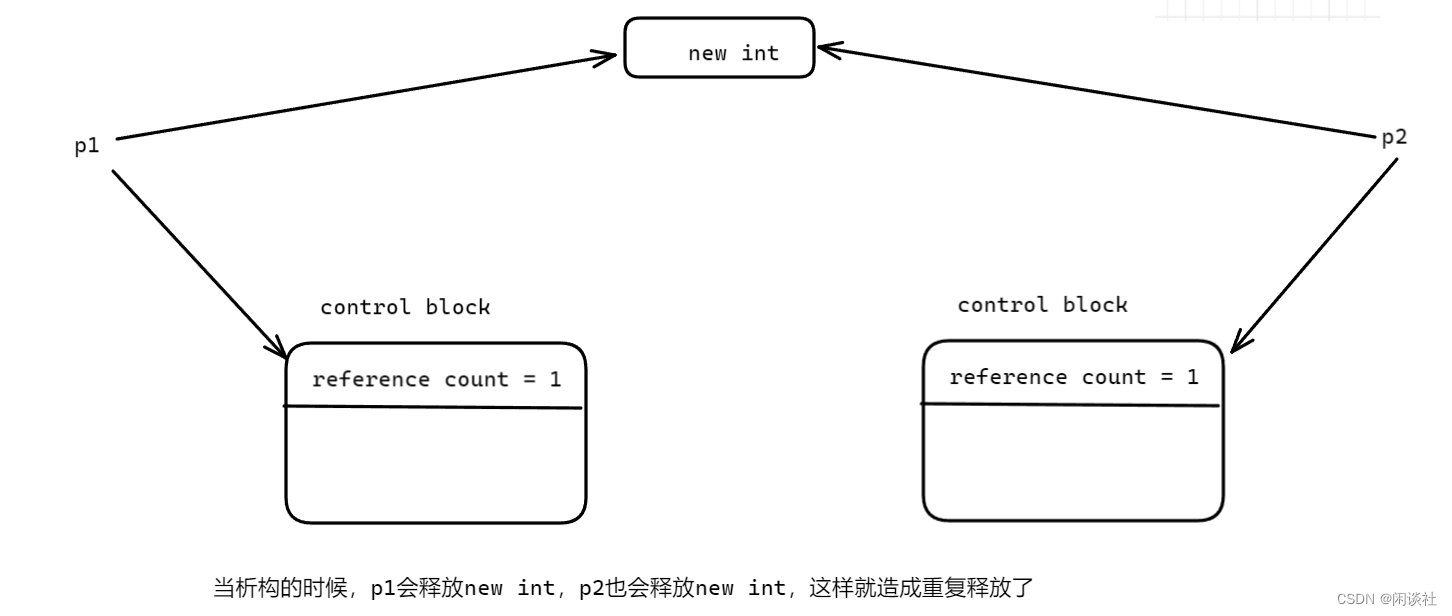
C++新特性:智能指针
一 、为什么需要智能指针 智能指针主要解决以下问题: 1)内存泄漏:内存手动释放,使用智能指针可以自动释放 2)共享所有权指针的传播和释放,比如多线程使用同一个对象时析构问题,例如同样的数据…...
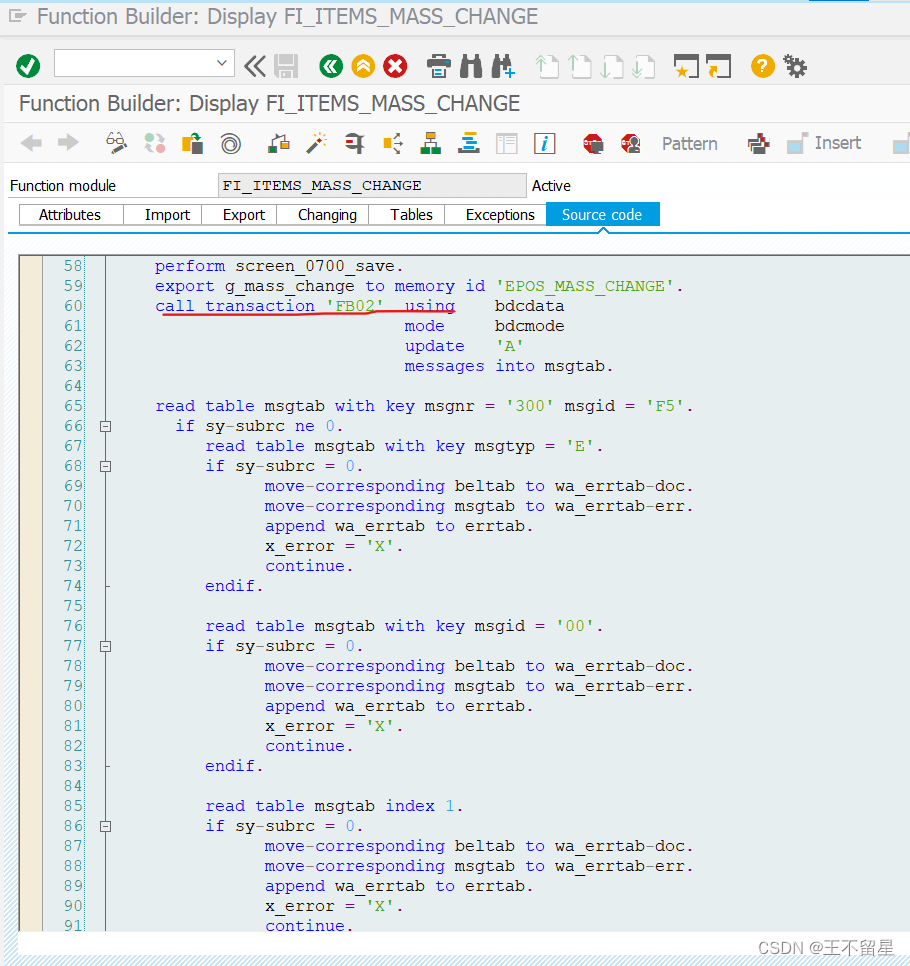
SAP FI之批量修改财务凭证的BAPI
文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 前言 一般涉及修改财务凭证,或者其它凭证,不应直接更新数据库,而是使用系统提供的function module,或者BAPI,或者使用BDC。 一、 示例…...

Spring Boot + Vue的网上商城之商品分类
Spring Boot Vue的网上商城之商品分类 在网上商城中,商品分类是非常重要的一个功能,它可以帮助用户更方便地浏览和筛选商品。本文将介绍如何使用Spring Boot和Vue来实现商品分类的功能,包括一级分类和二级分类的管理以及前台按分类浏览商品…...

Docker 容器逃逸漏洞 (CVE-2020-15257)复现
漏洞概述 containerd是行业标准的容器运行时,可作为Linux和Windows的守护程序使用。在版本1.3.9和1.4.3之前的容器中,容器填充的API不正确地暴露给主机网络容器。填充程序的API套接字的访问控制验证了连接过程的有效UID为0,但没有以其他方式…...
Python 如何使用 csv、openpyxl 库进行读写 Excel 文件详细教程(更新中)
csv 基本概述 首先介绍下 csv (comma separated values),即逗号分隔值(也称字符分隔值,因为分隔符可以不是逗号),是一种常用的文本格式,用以存储表格数据,包括数字或者字符。 程序在处理数据时…...

$nextTick属性使用与介绍
属性介绍 $nextTick 是 Vue.js 中的一个重要方法,之前我们也说过$ref 等一些重要的属性,这次我们说$nextTick,$nextTick用于在 DOM 更新后执行回调函数。它通常用于处理 DOM 更新后的操作,因为 Vue 在更新 DOM 后不会立即触发回调…...

【群智能算法改进】一种改进的鹈鹕优化算法 IPOA算法[2]【Matlab代码#58】
文章目录 【获取资源请见文章第5节:资源获取】1. 原始POA算法2. 改进后的IPOA算法2.1 随机对立学习种群初始化2.2 动态权重系数2.3 透镜成像折射方向学习 3. 部分代码展示4. 仿真结果展示5. 资源获取 【获取资源请见文章第5节:资源获取】 1. 原始POA算法…...

k8s 入门到实战--部署应用到 k8s
k8s 入门到实战 01.png 本文提供视频版: 背景 最近这这段时间更新了一些 k8s 相关的博客和视频,也收到了一些反馈;大概分为这几类: 公司已经经历过服务化改造了,但还未接触过云原生。公司部分应用进行了云原生改造&…...

编程语言新特性:instanceof的改进
以前也写过类似的博文,可能重复。 要判断一个对象是哪个类或父类的实例,JAVA用到instanceof,其实语言也有类似语法。而类一般是多层继承的,有时就让人糊涂。所以我提出改进思路: instanceof:保持不变。ins…...
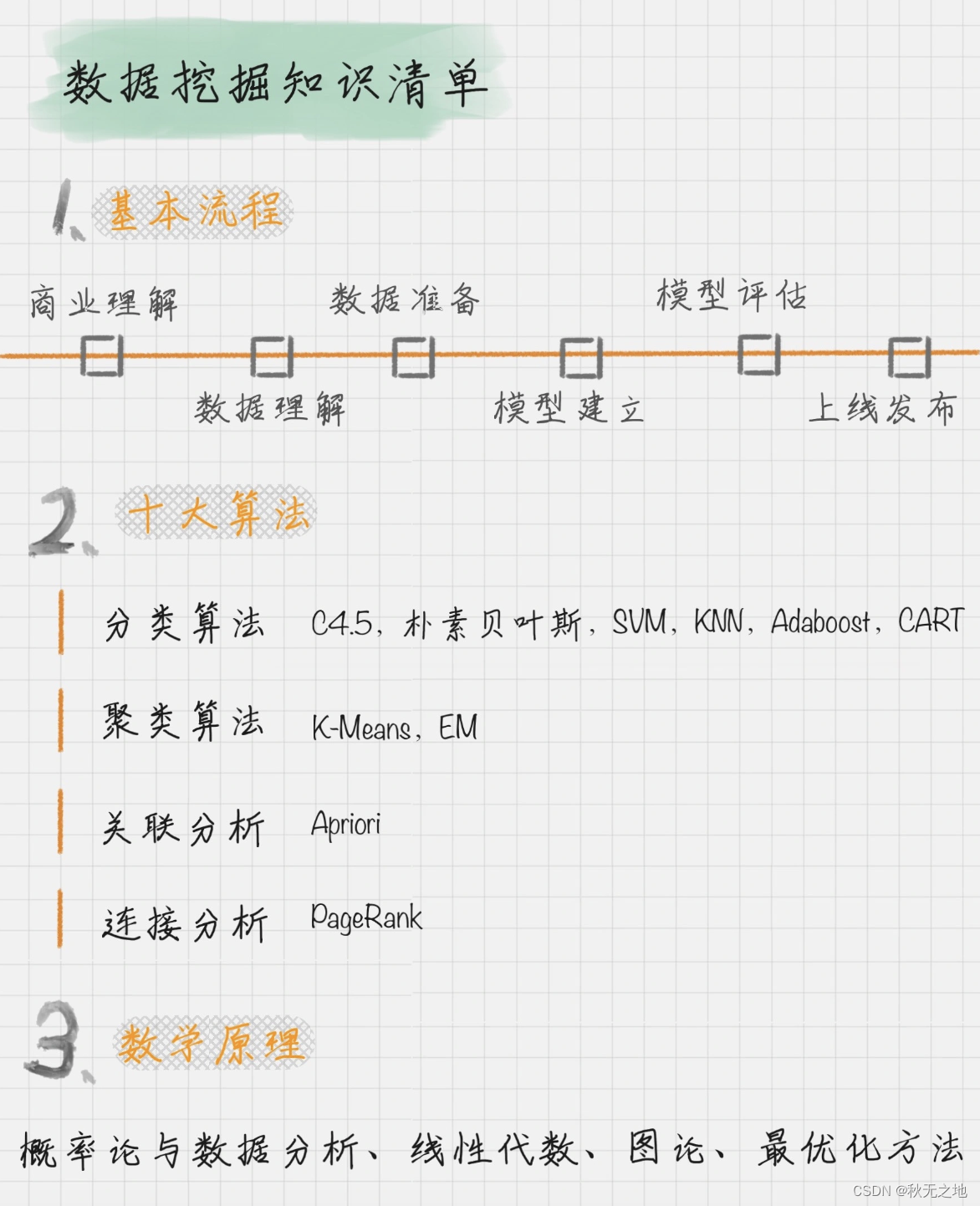
数据挖掘的学习路径
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...
逻辑回归Logistic
回归 概念 假设现在有一些数据点,我们用一条直线对这些点进行拟合(这条直线称为最佳拟合直线),这个拟合的过程就叫做回归。进而可以得到对这些点的拟合直线方程。 最后结果用sigmoid函数输出 因此,为了实现 Logisti…...
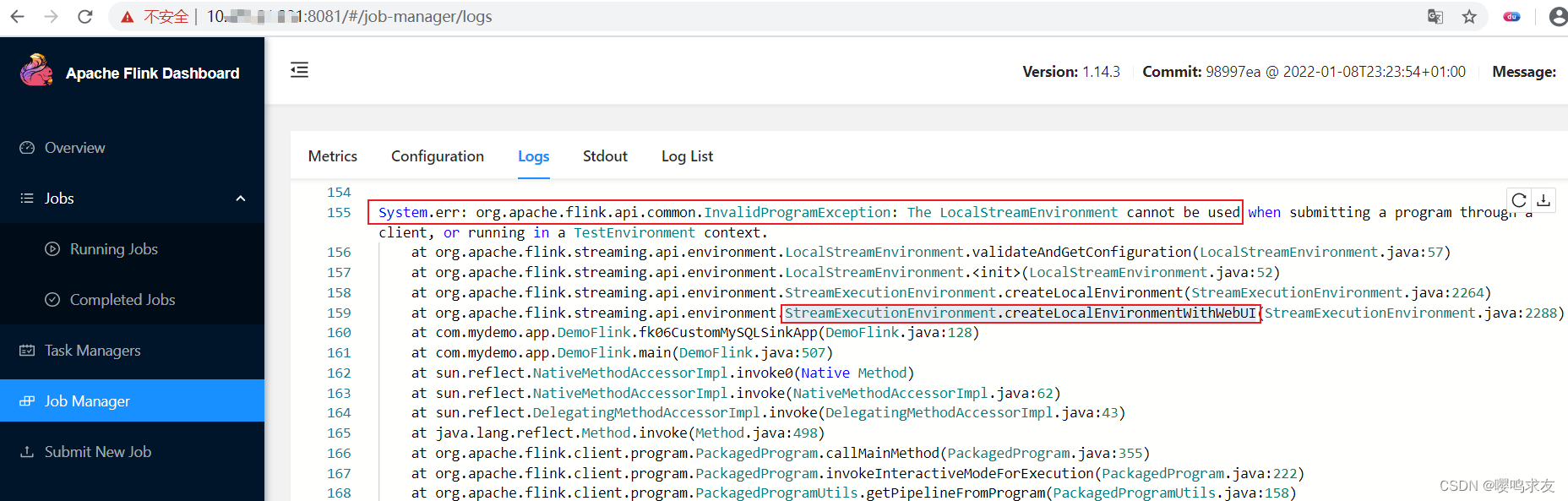
Flink提交jar出现错误RestHandlerException: No jobs included in application.
今天打包一个flink的maven工程为jar,通过flink webUI提交,发现居然报错。 如上图所示,提示错误为: Server Response Message: org.apache.flink.runtime.rest.handler.RestHandlerException: No jobs included in application. …...
】基础概念:数据仓库【用于决策的数据集合】的概念、建立数据仓库的原因与好处)
【数仓基础(一)】基础概念:数据仓库【用于决策的数据集合】的概念、建立数据仓库的原因与好处
文章目录 一. 数据仓库的概念1. 面向主题2. 集成3. 随时间变化4. 非易失粒度 二. 建立数据仓库的原因三. 使用数据仓库的好处 一. 数据仓库的概念 数据仓库的主要作用: 数据仓库概念主要是解决多重数据复制带来的高成本问题。 在没有数据仓库的时代,需…...
电商类面试问题--01Elasticsearch与Mysql数据同步问题
在实现基于关键字的搜索时,首先需要确保MySQL数据库和ES库中的数据是同步的。为了解决这个问题,可以考虑两层方案。 全量同步:全量同步是在服务初始化阶段将MySQL中的数据与ES库中的数据进行全量同步。可以在服务启动时,对ES库进…...
天线材质介绍--FPC天线
...

vue3 的 ref、 toRef 、 toRefs
1、ref: 对原始数据进行拷贝。当修改 ref 响应式数据的时候,模版中引用 ref 响应式数据的视图处会发生改变,但原始数据不会发生改变 <template><div>{{refA}}</div> </template><script lang"ts" setup> impor…...
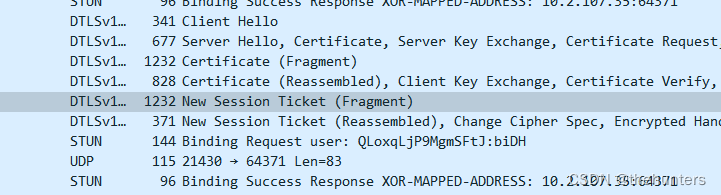
WebRTC中 setup:actpass、active、passive
1、先看一下整个DTLS的流程 setup:actpass、active、passive就发生在Offer sdp和Anser SDP中 Offer的SDP是setup:actpass,这个是服务方: v0\r o- 1478416022679383738 2 IN IP4 127.0.0.1\r s-\r t0 0\r agroup:BUNDLE 0 1\r aextmap-allow-mixed\r amsid-semanti…...

ModuleNotFoundError: No module named ‘lavis‘解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
