《蓝桥杯每日一题》并查集·AcWing1249. 亲戚
1.题目描述
或许你并不知道,你的某个朋友是你的亲戚。
他可能是你的曾祖父的外公的女婿的外甥女的表姐的孙子。
如果能得到完整的家谱,判断两个人是否是亲戚应该是可行的,但如果两个人的最近公共祖先与他们相隔好几代,使得家谱十分庞大,那么检验亲戚关系实非人力所能及。
在这种情况下,最好的帮手就是计算机。
为了将问题简化,你将得到一些亲戚关系的信息,如Marry和Tom是亲戚,Tom和Ben是亲戚,等等。
从这些信息中,你可以推出Marry和Ben是亲戚。
请写一个程序,对于我们的关于亲戚关系的提问,以最快的速度给出答案。
输入格式
输入由两部分组成。
第一部分以 N,M 开始。N 为问题涉及的人的个数。这些人的编号为 1,2,3,…,N。下面有 M 行,每行有两个数 ai,bi,表示已知 ai 和 bi是亲戚。
第二部分以 Q开始。以下 Q 行有 Q 个询问,每行为 ci,di,表示询问 ci 和 di 是否为亲戚。
输出格式
对于每个询问 ci,di,输出一行:若 ci和 di 为亲戚,则输出“Yes”,否则输出“No”。
数据范围
1≤N≤20000
1≤M≤10的六次方
1≤Q≤10的六次方
输入样例:
10 7
2 4
5 7
1 3
8 9
1 2
5 6
2 3
3
3 4
7 10
8 9
输出样例:
Yes
No
Yes
2.思路分析
我们先初始化p数组
然后输入m个数
我们查询一下,如果root1(find(a),即a的根节点)不是root2(find(b),即b的根节点),我们就把它们连接起来
最后输入q个数判断一下就行了,如果它们都是一个祖宗,我们就输出Yes,反之输出No
注意用BufferedReader和BufferedWriter优化一下输入输出,不然会超时
关于快速输入可以看一下我的这篇博客
https://blog.csdn.net/m0_68055637/article/details/128551437
3.Ac代码
import java.io.*;public class Main {static int N=20010;static int []p=new int[N]; //存储每个点的祖宗节点public static void main(String[] args) throws IOException {BufferedReader br=new BufferedReader(new InputStreamReader(System.in));BufferedWriter bw=new BufferedWriter(new OutputStreamWriter(System.out));String []s=br.readLine().split(" ");int n=Integer.parseInt(s[0]),m=Integer.parseInt(s[1]);for (int i = 0; i < n; i++) {p[i]=i;}while (m-->0){s=br.readLine().split(" ");int a=Integer.parseInt(s[0]),b=Integer.parseInt(s[1]);int root1=find(a),root2=find(b); //分别找到两个人的祖宗节点,并判断是不是亲戚if(root1!=root2) p[root1]=root2; //如果不是,添加至同族}int t=Integer.parseInt(br.readLine());while (t-->0){s=br.readLine().split(" ");int a=Integer.parseInt(s[0]),b=Integer.parseInt(s[1]);bw.write(find(a)==find(b)?"Yes":"No");bw.newLine(); //换行}bw.flush(); //输出缓冲区才能输出}private static int find(int x) {if(p[x]!=x) p[x]=find(p[x]);return p[x];}
}
感谢你能看完, 如有错误欢迎评论指正,有好的思路可以交流一波,如果对你有帮助的话,点个赞支持下
相关文章:

《蓝桥杯每日一题》并查集·AcWing1249. 亲戚
1.题目描述或许你并不知道,你的某个朋友是你的亲戚。他可能是你的曾祖父的外公的女婿的外甥女的表姐的孙子。如果能得到完整的家谱,判断两个人是否是亲戚应该是可行的,但如果两个人的最近公共祖先与他们相隔好几代,使得家谱十分庞…...
亚马逊云科技依托人工智能进行游戏数据分析,解决游戏行业痛点,助力游戏增长
前言 据互联网数据显示:2014 年我国游戏行业用户规模为 517.31 百万人,直至 2020 年达 554.79 百万人;同时,2020 年,我国游戏市场实际销售收入 2786.87 亿元,比 2019 年增加了478.1 亿元,…...

为什么不建议用 equals 判断对象相等?
一直以为这个方法是java8的,今天才知道是是1.7的时候,然后翻了一下源码。 这片文章中会总结一下与a.equals(b)的区别,然后对源码做一个小分析。 一,值是null的情况: 1.a.equals(b), a 是null, 抛出NullPointExcepti…...

手写线程池实例并测试
前言:在之前的文章中介绍过线程池的核心原理,在一次面试中面试官让手写线程池,这块知识忘记的差不多了,因此本篇文章做一个回顾。 希望能够加深自己的印象以及帮助到其他的小伙伴儿们😉😉。 如果文章有什么…...
实操go开发环境的配置
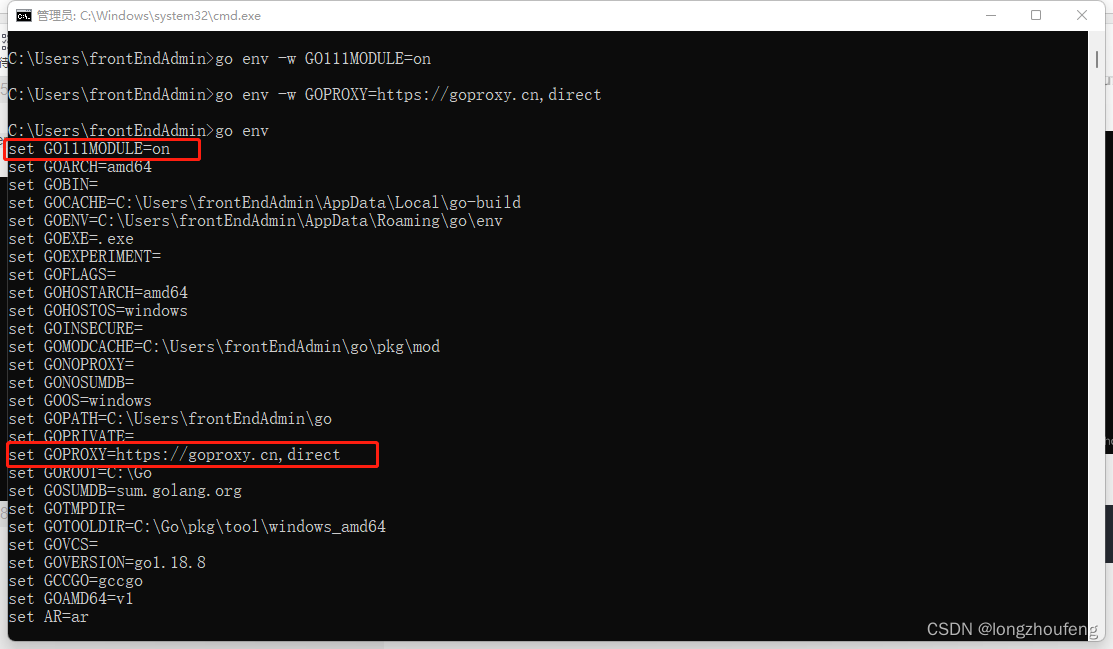
1、Go 安装包下载,下载地址如下: go语言中文网下载(本人电脑的系统是Windows,这里以Windows版本的安装包为例,安装就是傻瓜式安装,只要点下一步–下一步–完成就可以了,本人安装在C盘下。 我…...
)
华为OD机试真题Python实现【匿名信】真题+解题思路+代码(20222023)
匿名信 题目 电视剧《分界线》里面有一个片段,男主为了向警察透露案件细节,且不暴露自己,于是将报刊上的字减下来,剪拼成匿名信。 现在又一名举报人,希望借鉴这种手段,使用英文报刊完成举报操作。 但为了增加文章的混淆度,只需满足每个单词中字母数量一致即可,不关注…...
)
阿里淘系面试经历(一)
文章目录 1、JVM讲一下,尽你所知道的1. 类的加载过程1.1 加载过程介绍1.2 类加载流程1.3 类加载器2. 垃圾回收2.1 如何确定对象已死2.2 垃圾回收算法2.2.1 标记--清除算法2.2.2 复制算法2.2.3 标记--整理算法2.3 垃圾收集器2.3.1 Serial 收集器2.3.2 ParNew 收集器2.3.3 Paral…...
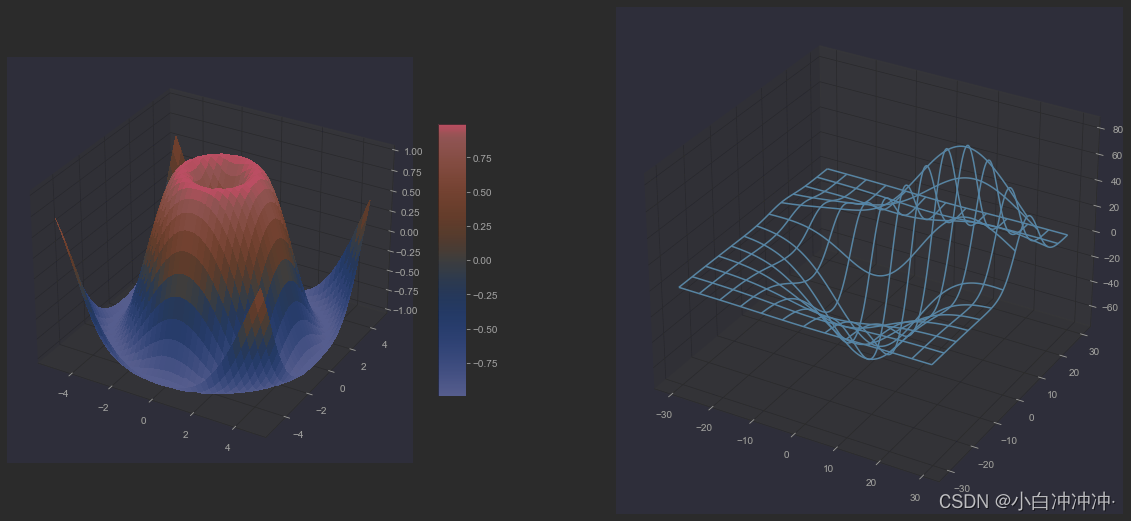
matplotlib绘制三维图
目录线状堆积图 PolygonPlot三维表面图 SurfacePlot散点图ScatterPlot柱形图 BarPlot三维直方图螺旋曲线图 LinePlotContourPlot轮廓图网状图 WireframePlot箭头图二维三维合并文本图Text三维多个子图线状堆积图 PolygonPlot Axes3D.add_collection3d(col, zs0, zdir‘z’) …...
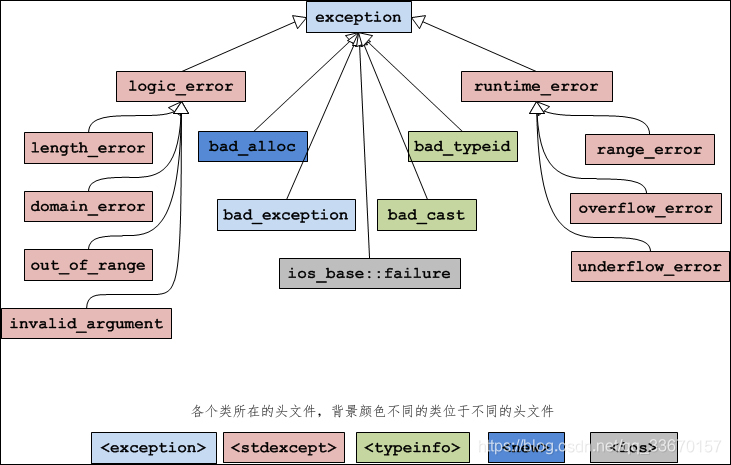
4万字c++讲解+区分c和c++,不来可惜了(含代码+解析)
目录 1 C简介 1.1 起源 1.2 应用范围 1.3 C和C 2开发工具 3 基本语法 3.1 注释 3.2关键字 3.3标识符 4 数据类型 4.1基本数据类型 4.2 数据类型在不同系统中所占空间大小 4.3 typedef声明 4.4 枚举类型 5 变量 5.1 变量的声明和定义 5.2 变量的作用域 6 运算符…...

AcWing 482. 合唱队形
482. 合唱队形N 位同学站成一排,音乐老师要请其中的 (N−K) 位同学出列,使得剩下的 K 位同学排成合唱队形。 合唱队形是指这样的一种队形:设 K位同学从左到右依次编号为 1,2…,K,他们的身高分别为…...
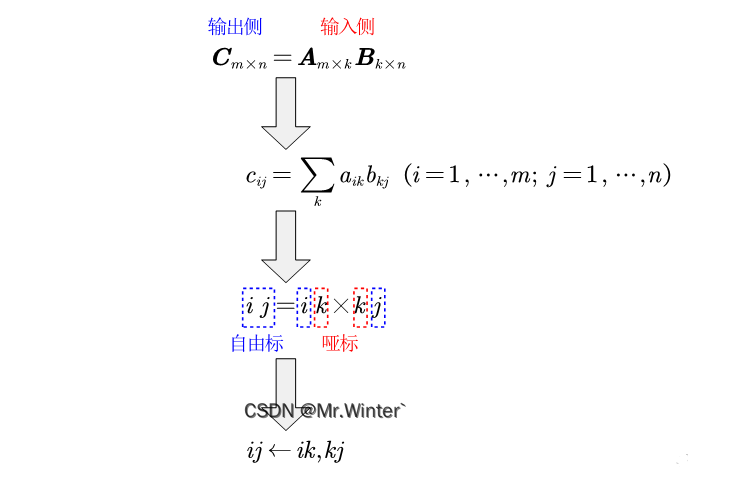
Pytorch深度学习实战3-4:通俗理解张量Tensor的爱因斯坦求和(附实例)
目录1 爱因斯坦求和由来2 爱因斯坦求和原理3 实例:字母表示法3.1 向量运算3.2 矩阵运算3.3 张量运算4 实例:常量表示法4.1 向量运算4.2 矩阵运算4.3 张量运算1 爱因斯坦求和由来 爱因斯坦求和约定(Einstein summation convention)是一种标记的约定&#…...
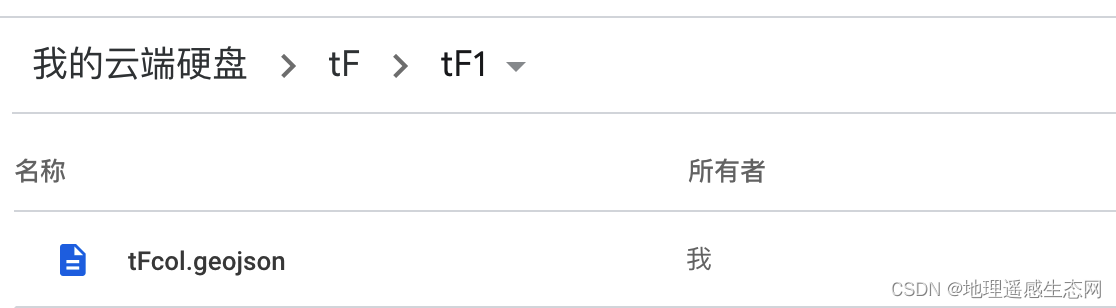
GEE学习笔记 五十六:GEE中如何把文件导出到Google Drive的子目录
今天在群里看到有人在问一个问题,如何使用GEE把文件导出到Google Drive的子目录中?这里我就简单的说一下这个问题。 首先,在GEE中我们都知道了如何将数据导出导出Google Drive的文件夹中,如下面的一个例子: var geome…...

【Go基础】数据库编程
文章目录1. SQL语法简介2. MySQL最佳实践3. Go SQL驱动接口解读4. 数据库增删改查5. stmt6. SQLBuilder6.1 Go-SQLBuilder6.2 Gendry6.3 自行实现SQLBuilder7. GORM8. Go操作MongoDB1. SQL语法简介 SQL(Structured Query Language)是一套语法标准&#…...

【颠覆软件开发】华为自研IDE!未来IDE将不可预测!
IDE是软件开发生态的入口,但目前我们所使用的IDE基本都是由国外巨头提供,比如Visual Studio、Eclipse、JetBrains。这些IDE具有很高的断供风险,与操作系统、芯片、编程语言一样,非常重要。 随着越来越多的软件开始采用云上开发模…...

怎样从零基础学黑客
可以说想学黑客技术,要求你首先是一个“T”字型人才,也就是说电脑的所有领域你都能做的来,而且有一项是精通的。因此作为一个零基础的黑客爱好者来说,没有良好的基础是绝对不行的,下面我就针对想真正学习黑客的零基础朋…...
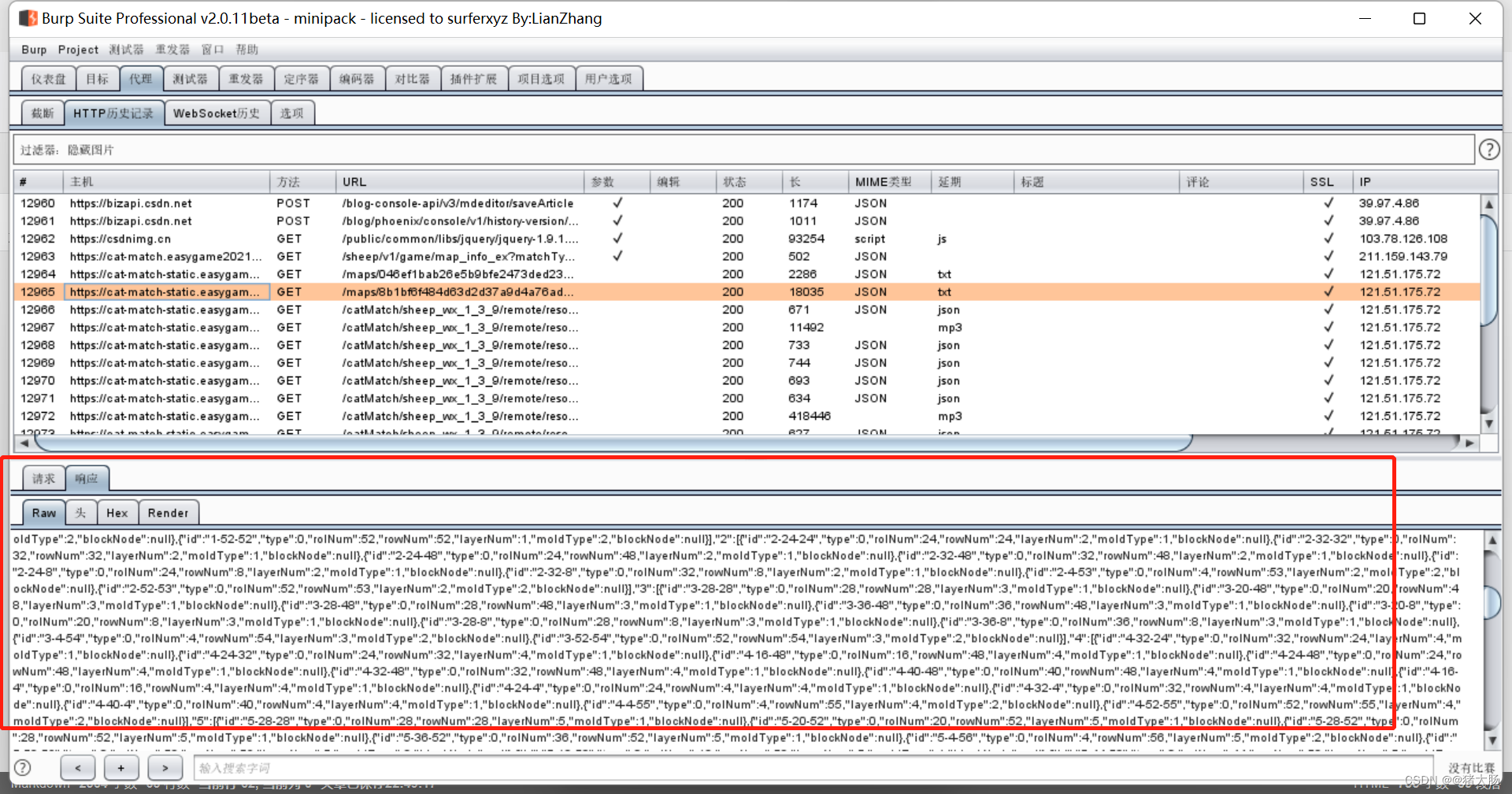
burp小程序抓包
身为一名码农,抓包肯定是一项必备技能。工作中遇到很多次需要对小程序进行抓包排查问题。下面分享一下我的抓包方式,使用的是电脑版小程序抓包,跟手机的方式都差不多的。 一、环境 微信版本:3.6.0.18 Burpsuite版本:…...

文件上传攻击骚操作
允许直接上传shell 只要有文件上传功能,那么就可以尝试上传webshell直接执行恶意代码,获得服务器权限,这是最简单也是最直接的利用。 允许上传压缩包 如果可以上传压缩包,并且服务端会对压缩包解压,那么就可能存在Zip …...
Scala流程控制(第四章:分支控制、嵌套分支、switch分支、for循环控制全、while与do~while、多重与中断)
文章目录第 4 章 流程控制4.1 分支控制 if-else4.1.1 单分支4.1.2 双分支4.1.3 多分支4.2 嵌套分支4.3 Switch 分支结构4.4 For 循环控制4.4.1 范围数据循环(To)4.4.2 范围数据循环(Until)4.4.3 循环守卫4.4.4 循环步长4.4.5 嵌套…...
)
华为OD机试真题Python实现【整理扑克牌】真题+解题思路+代码(20222023)
整理扑克牌 题目 给定一组数字,表示扑克牌的牌面数字,忽略扑克牌的花色,请安如下规则对这一组扑克牌进行整理。 步骤一: 对扑克牌进行分组,规则如下 当牌面数字相同张数大于等于4时,组合牌为炸弹;三张相同牌面数字+两张相同牌面数字,且三张牌与两张牌不相同时,组合牌…...
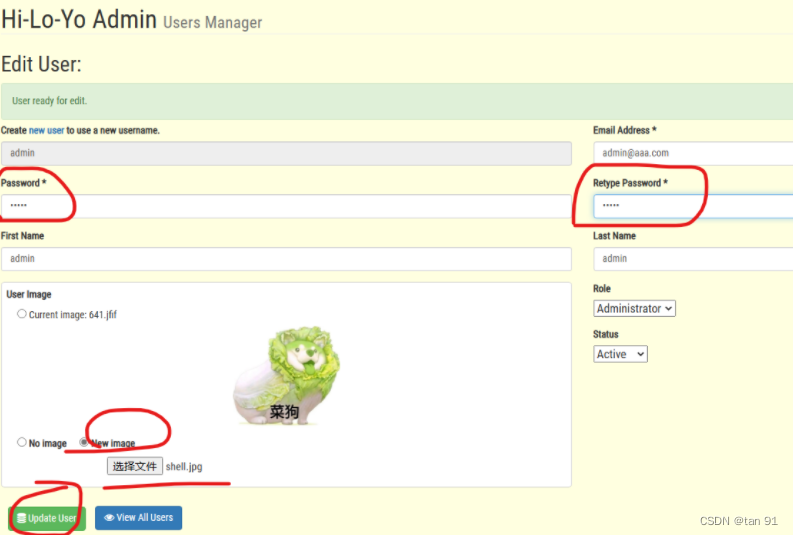
【春秋云境】CVE-2022-28525
靶标介绍: ED01-CMS v20180505 存在任意文件上传漏洞 打开靶场: 盲猜一波弱密码admin:admin就进去了。登录后在图中位置点击进行图片更新,需要将密码等都写上 抓包将图片信息进行替换,并修改文件名: POST /admin…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
