mysql基于AES_ENCRYPTAES_DECRYPT实现密码的加密与解密
1.直接使用AES_ENCRYPT&&AES_DECRYPT函数导致的问题。
执行语句
select AES_ENCRYPT('cd123','key')结果 加密过后的字符串是一串很奇怪的字符。
 尝试使用上面加密过后的字符解密。
尝试使用上面加密过后的字符解密。
select AES_DECRYPT('Äu5£dö|#餹','key')结果 并未成功的解密

2.解决办法
使用 hex() 和 unhex()处理密码。
2.1 hex()与unhex()函数
hex():将一个字符串或数字转换为十六进制格式的字符串。
unhex():把十六进制格式的字符串转化为原来的格式。每对十六进制数字转化为一个字符。执行hex(str)的逆运算。即,它将参数中的每对十六进制数字解释为一个数字,并将其转换为该数字表示的字符。结果字符将作为二进制字符串返回。参数字符串中的字符必须为合法的十六进制数字:“ 0” ..“ 9”,“ A” ..“ F”,“ a” ..“ f”。如果UNHEX在参数中遇到任何非十六进制数字,则返回NULL。
2.2 加密SQL
select hex(AES_ENCRYPT('cd123','key'))2.3 结果
如此加密可以直接使用varchar类型直接存储。
 2.4 解密SQL
2.4 解密SQL
SELECT AES_DECRYPT(UNHEX('C4753517A364960F83F67C7F23E9A4B9'),'key')2.5 结果

相关文章:

mysql基于AES_ENCRYPTAES_DECRYPT实现密码的加密与解密
1.直接使用AES_ENCRYPT&&AES_DECRYPT函数导致的问题。 执行语句 select AES_ENCRYPT(cd123,key) 结果 加密过后的字符串是一串很奇怪的字符。 尝试使用上面加密过后的字符解密。 select AES_DECRYPT(u5£d|#,key) 结果 并未成功的解密 2.解决办法 使用 hex(…...
怎么把pdf转换成jpg图片?
怎么把pdf转换成jpg图片?在工作中,如果我们收到无法修改编辑的PDF文件,可能会遇到一些困难。尤其是当平台或网站只支持JPG图片格式,而领导又要求我们将pdf文件改为JPG格式时,情况就更为棘手了。这对于我们打工一族来说…...

计算机脚本的概念,如何编写、使用脚本 (Script)?
一、脚本的概念和使用场景 在计算机领域的脚本,指的是使用一种特定的描述性语言,依据一定的格式编写的可执行文件脚本语言又被称为扩建的语言或者动态语言, 是一种编程语言, 用来控制软件应用程序, 脚本通常是以文本 (ASCⅡ) 保存, 只是在被调用时进行解…...

c语言 5.0
💂 个人主页: 程序员爱摸鱼🤟 版权: 本文由【程序员爱摸鱼】原创、在CSDN首发、需要转载请联系博主💬 如果文章对你有帮助、欢迎关注点赞收藏(一键三连)哦💅 想寻找共同成长的小伙伴,可以互粉哦 💬文章目录…...
如何配置远程访问以在外部网络中使用公司内部的OA办公系统——“cpolar内网穿透”
文章目录 前言1. 确认在内网下能够使用IP端口号登录OA办公系统2. 安装cpolar内网穿透3. 创建隧道映射内网OA系统服务端口4. 实现外网访问公司内网OA系统总结 前言 现在大部分公司都会在公司内网搭建使用自己的办公管理系统,如OA、ERP、金蝶等,员工只需要…...
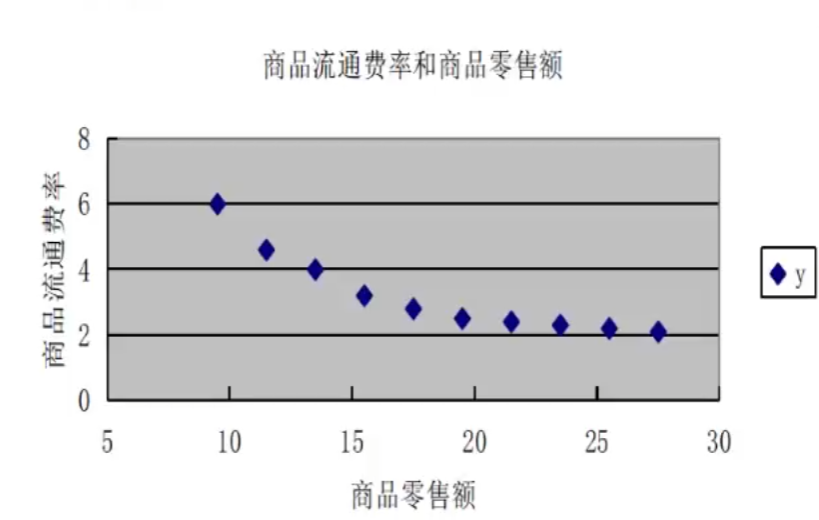
【AI】机器学习——线性模型(线性回归)
线性模型既能体现出重要的基本思想,又能构造出功能更加强大的非线性模型 文章目录 3.1 线性模型3.1.1 数据3.1.2 目标/应用 3.2 线性回归3.2.1 回归模型历史3.2.2 回归分析研究内容回归分析步骤 3.2.3 回归分析分类3.2.4 回归模型3.2.5 损失函数梯度下降法一元回归模…...
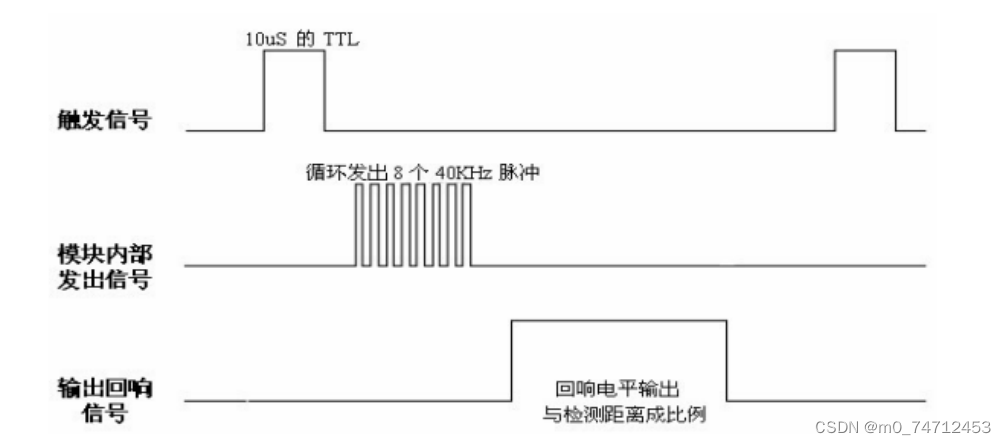
智能小车之跟随小车、避障小车原理和代码
目录 1. 红外壁障模块分析编辑 2. 跟随小车的原理 3. 跟随小车开发和调试代码 4. 超声波模块介绍 5. 摇头测距小车开发和调试代码 1. 红外壁障模块分析 原理和循迹是一样的,循迹红外观朝下,跟随朝前 TCRT5000传感器的红外发射二极管不断发射红外…...
行业追踪,2023-09-07
自动复盘 2023-09-07 凡所有相,皆是虚妄。若见诸相非相,即见如来。 k 线图是最好的老师,每天持续发布板块的rps排名,追踪板块,板块来开仓,板块去清仓,丢弃自以为是的想法,板块去留让…...
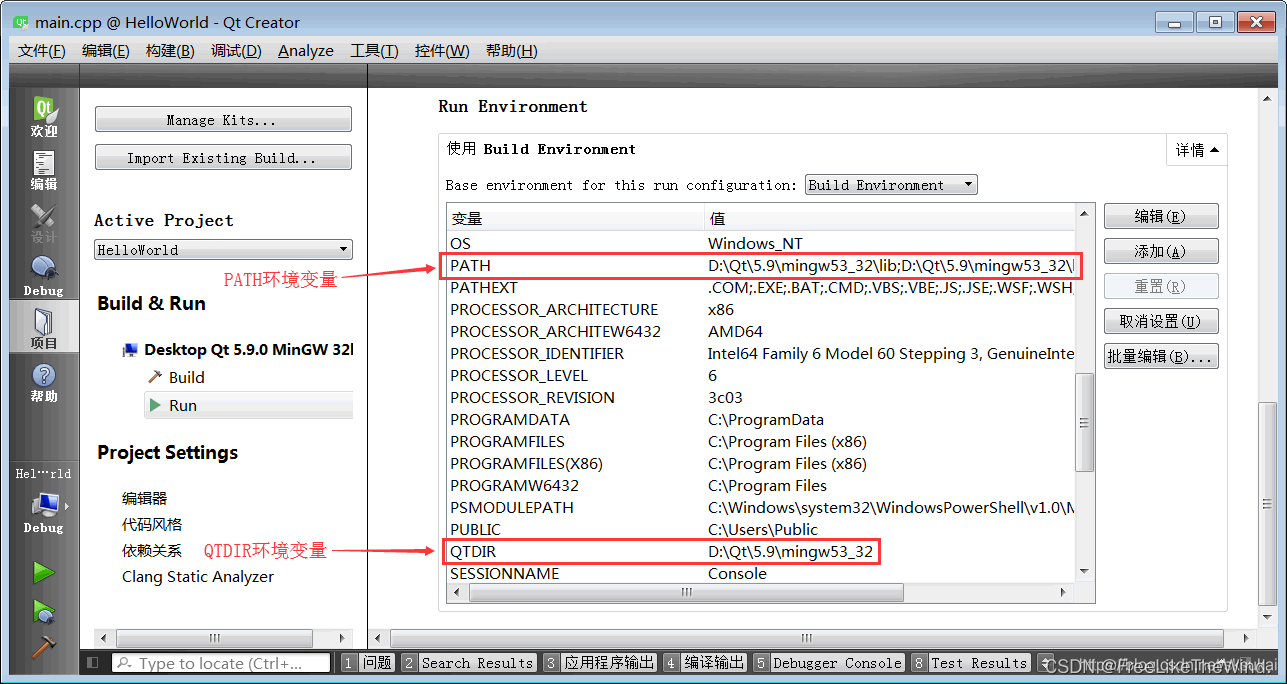
Qt creator中项目的构建配置和运行设置
使用 Qt Creator 集成开发环境构建和运行程序是一件非常简单的事情,一个按钮或者一个快捷键搞定全部,大家已经都了解了。但是,这些看起来简单的过程,背后到底发生了什么呢? 点击 Qt Creator 项目模式,可以…...

蓝桥杯打卡Day3
文章目录 吃糖果递推数列 一、吃糖果IO链接 本题思路:本题题意就是斐波那契数列! #include <bits/stdc.h>typedef uint64_t i64;i64 f(i64 n) {if(n1) return 1;if(n2) return 2;return f(n-1)f(n-2); }signed main() {std::ios::sync_with_stdio(false);s…...

Linux系统编程--IO
文章目录 一、系统调用1.open()1.1 所需基础知识1.2. open() 详解1.3 示例代码 二、标准IO三、高级IO 一、系统调用 1.open() 1.1 所需基础知识 Linux遵循一切皆是文件的理念,因此,很多的交互工作都是通过读取和写入文件来完成。 文件必须被打开才能被…...
亚马逊云科技通过生成式AI,帮助清华RIOS加速计算和分析的处理效率
近日,硬件创建平台Efabless宣布了其第一届“生成式AI开源芯片设计挑战赛”(AI Generated Open-Source Silicon Design Challenge)的评选结果。来自清华大学的RISC-V国际开源实验室(RIOS Lab)团队基于亚马逊云科技云上科…...

全志T113-S3入门资料汇总(避坑指南)一
也是闲着无事买了个芒果派的T113的小板子,因为自己以前搞过Linux,工作也跟Linux相关,本以为可以很快搞好开发环境,结果还是折腾了两个周末,所以就把资料整理下,关键的地方列出来,希望大家少走弯…...

3dMax全球学习资源、资源文件和教程 !
此样例教育教程和学习资源旨在提供使用Autodesk 3ds Max时的计划知识和培训、正确的工作流、流程管理和最佳实践。 您在Autodesk三维设计领域的职业生涯 有关使用3ds Max和Maya在计算机图形领域开始职业生涯的提示(包括新的3ds Max和Maya介绍教程,以复…...

API接口是什么?有哪些免费的API接口?
API(接口)是什么? 举个常见的例子,在京东上下单付款之后,商家选用顺丰发货,然后你就可以在京东上实时查看当前的物流信息。京东和顺丰作为两家独立的公司,为什么会在京东上实时看到顺丰的快递信…...

USB Server应用于汇丰晋信基金
为了满足UKey远程连接调用、安全集群管理需求,汇丰晋信基金选择了朝天椒USB Server作为其解决方案。朝天椒USB Server以其卓越的性能和可靠性,为汇丰晋信基金提供了稳定的Ukey连接管理服务。这一选择不仅提高了汇丰晋信基金的工作效率,还保障…...
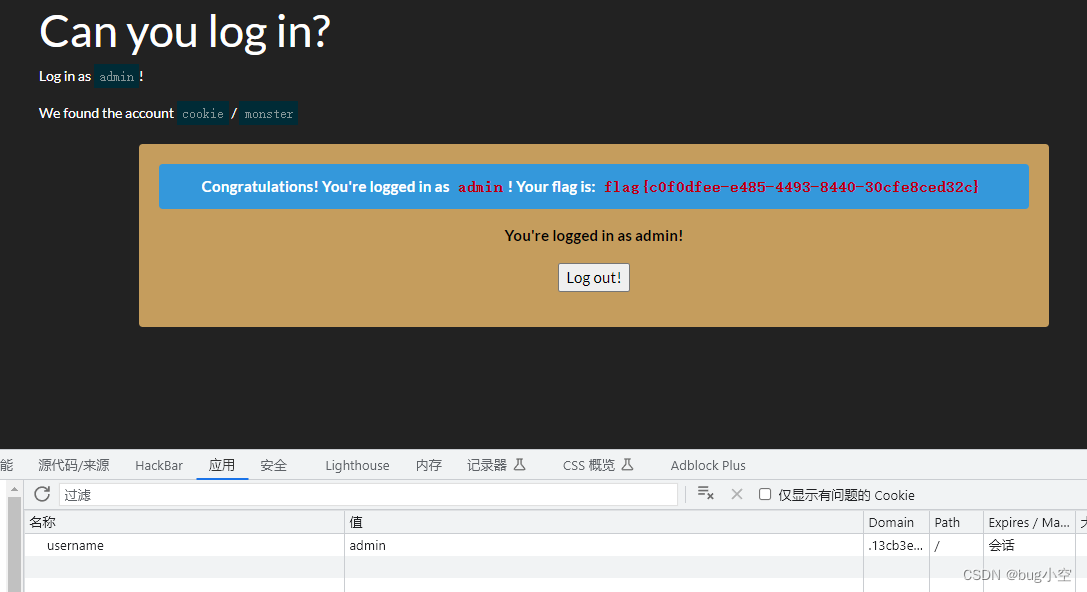
[BSidesCF 2019]Kookie 1 , cookie伪造
给了一个用户和密码 用户名:cookie 密码:monster 登录后查看cookie 发现就是用户名维持登录 那么修改用户名为 admin 得到flag...

如何查看MySQL的安装位置
MySQL的安装位置 1、查看安装目录 参数 路径 解释 备注 --basedir /usr/bin 相关命令目录 mysqladmin mysqldump等命令 --datadir /var/lib/mysql/ mysql 数据库文件的存放路径 --plugin-dir /usr/lib64/mysql/plugin mysql插件存放路径 --log-error …...

ui设计岗位招聘要求有哪些? 优漫动游
UI设计师的工作是接到使用者轮廓、线框草稿后,创造出好看、好用的画面,视情况会搭配VisualDesigner(视觉设计师),不过偶尔还是需要自己做图,包含插图、icon绘制等;透过设计过的画面,…...

Swift报错:“‘nil‘ is incompatible with return type ‘User‘”
func getUserById(userId: Int) -> User {if (userId ! nil) {...}return nil } 上述代码报了一个错误:“nil is incompatible with return type User”,表示“nil”与返回类型“User”不兼容。 解决方案: 将返回值类型改为Optional类型…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
