CF1120 D. Power Tree 巧妙的图论转化
传送门
[前题提要]:无
题目描述:
就是给你一棵树,然后每个点有花费,然后你可以选一个点,付费后对这个点的子树的所有叶子结点增减任意权值.
考虑有一个人会给这棵树的所有叶子结点赋值(值我们不知道),输出最小的花费,使得无论它如何赋值,我们使用上述的花
费都能使所有的叶子节点变为0
考虑对一个点的子树的所有叶子节点进行增减任意值.不难联想到对一个点的子树的所有节点增减任意值的做法.所以考虑使用类似于树链剖分的方式将树上修改化为链上区间修改.
考虑记录一个点的所有叶子节点,并且按照 d f s dfs dfs序将其离散化存下.按照 d f s dfs dfs序的性质,我们会发现一个点的所有叶子节点必然是连续的区间.那么此时我们的问题就变成了:
给你 n n n个可以修改的区间,每一个区间都有其修改范围,修改每一个区间需要一定花费,问你至少需要多少花费将所有数字变为0
考虑到区间修改以及单点查询,我们想到使用差分来解决.假设我们使用一个差分数组 k [ i ] = a [ i ] − a [ i − 1 ] k[i]=a[i]-a[i-1] k[i]=a[i]−a[i−1],那么对于每一次区间修改来说,我们都是 a [ l ] + = v a l , a [ r + 1 ] − = v a l a[l]+=val,a[r+1]-=val a[l]+=val,a[r+1]−=val,那么最终我们需要得到的所有的 k [ i ] = = 0 k[i]==0 k[i]==0.
此时有一个巧妙的转化,考虑我们需要所有的k[i]变为0,但是显然我们的差分数组是不改变前缀和的,所以此时所有的值肯定都转移到了cnt+1的位置(假设我们有cnt个叶子节点),那么对于我们的数的转移来说,我们只能将 l l l转移到 r + 1 r+1 r+1,如果我们将转移过程看成边,将每一个叶子结点看成点,那么我们想将所有的值都转移到 c n t + 1 cnt+1 cnt+1,就需要所有的点都联通才行,这样才能保证无论怎么赋值我们都可以将其转移到 c n t + 1 cnt+1 cnt+1的位置
那么此时这道题就简单了,考虑到必须所有点都联通,每次选择联通一个点我们都需要花费,又需要花费最小,所以显然是个最小生成树的模型,此时使用最小生成树跑一下就行.
但是还有一个问题,那就是这道题的最终问题是所有的可能性的最小生成树的点,所以我们用朴素的 k r u s k a l kruskal kruskal跑出来的只是一棵树,需要改一下.考虑到最小生成树的性质,当边相同时,我们可以选择任意一条不在联通块中的边,所以这些边显然都是平等的,所以这些边都是我们的答案(当然这一点是可以严谨证明的,但是限于篇幅,此处不再赘述)
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
inline void print(__int128 x){if(x<0) {putchar('-');x=-x;}if(x>9) print(x/10);putchar(x%10+'0');
}
#define maxn 1000000
#define int long long
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int w[maxn];vector<int>edge[maxn];int l[maxn],r[maxn];
int cnt=0;
void dfs(int u,int per_u) {if(edge[u].size()==1&&u!=1) {++cnt;l[u]=r[u]=cnt;}for(auto v:edge[u]) {if(v==per_u) continue;dfs(v,u);l[u]=min(l[u],l[v]);r[u]=max(r[u],r[v]);}
}
struct Edge{int u,v,w,id;bool operator < (const Edge &rhs) const {return w<rhs.w;}
}edge2[maxn];
int fa[maxn];
int find(int x) {if(x==fa[x]) return x;else return fa[x]=find(fa[x]);
}
signed main() {int n=read();for(int i=1;i<=n;i++) {w[i]=read();}for(int i=1;i<n;i++) {int u=read();int v=read();edge[u].push_back(v);edge[v].push_back(u);}memset(l,0x3f,sizeof l);memset(r,-0x3f,sizeof r);dfs(1,0);for(int i=1;i<=n;i++) {int u=l[i],v=r[i];edge2[i]={u,v+1,w[i],i};}for(int i=1;i<=cnt;i++) fa[i]=i;sort(edge2+1,edge2+1+n);vector<int>ans;int this_cnt=0;int need=0;for(int i=1;i<=n;i++) {int r=i;while(r+1<=n&&edge2[r+1].w==edge2[r].w) r++;for(int j=i;j<=r;j++) {auto [u,v,w,k]=edge2[j];if(find(u)!=find(v)) {this_cnt++;ans.push_back(k);}}for(int j=i;j<=r;j++) {auto [u,v,w,k]=edge2[j];if(find(u)!=find(v)) {need+=w;fa[find(u)]=find(v);}}i=r;}sort(ans.begin(),ans.end());cout<<need<<" "<<ans.size()<<endl;for(auto i:ans) cout<<i<<" ";return 0;
}
相关文章:

CF1120 D. Power Tree 巧妙的图论转化
传送门 [前题提要]:无 题目描述: 就是给你一棵树,然后每个点有花费,然后你可以选一个点,付费后对这个点的子树的所有叶子结点增减任意权值. 考虑有一个人会给这棵树的所有叶子结点赋值(值我们不知道),输出最小的花费,使得无论它如何赋值,我们使用上述的花 费都能使所有的叶子…...
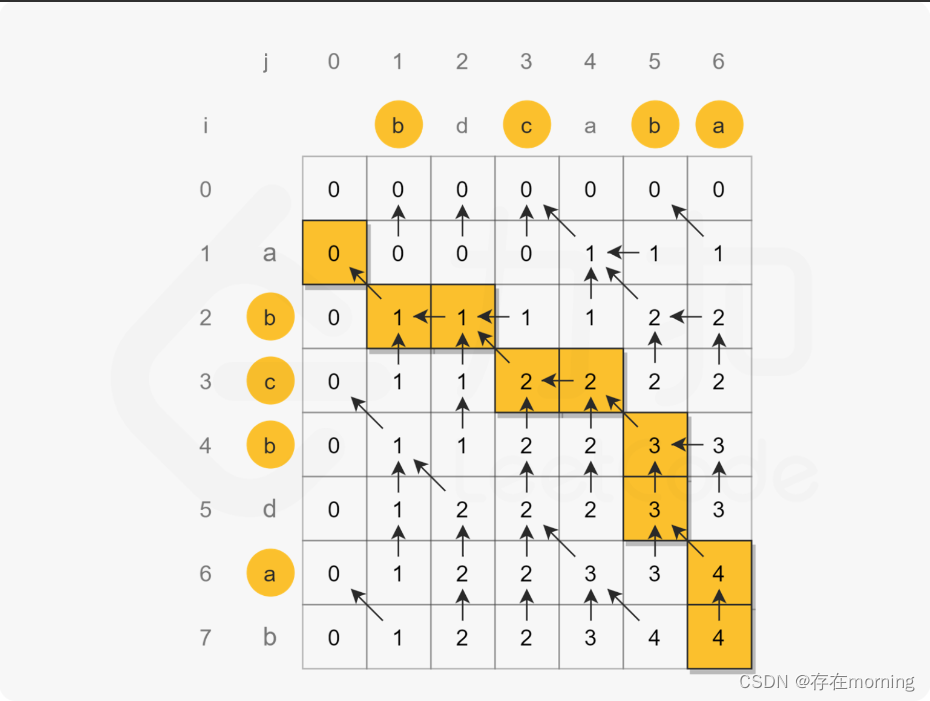
【算法训练-字符串 三】最长公共子串、最长公共子序列
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【】,使用【】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为:目标公…...

lintcode 1446 · 01矩阵走路问题 【两次BFS, VIP 中等 1也计算距离,但是不入队列】
题目链接,描述 https://www.lintcode.com/problem/1446 给定一个大小为 n*m 的 01 矩阵 grid ,1 是墙,0 是路,你现在可以把 grid 中的一个 1 变成 0,请问从左上角走到右下角是否有路可走?如果有路可走&am…...
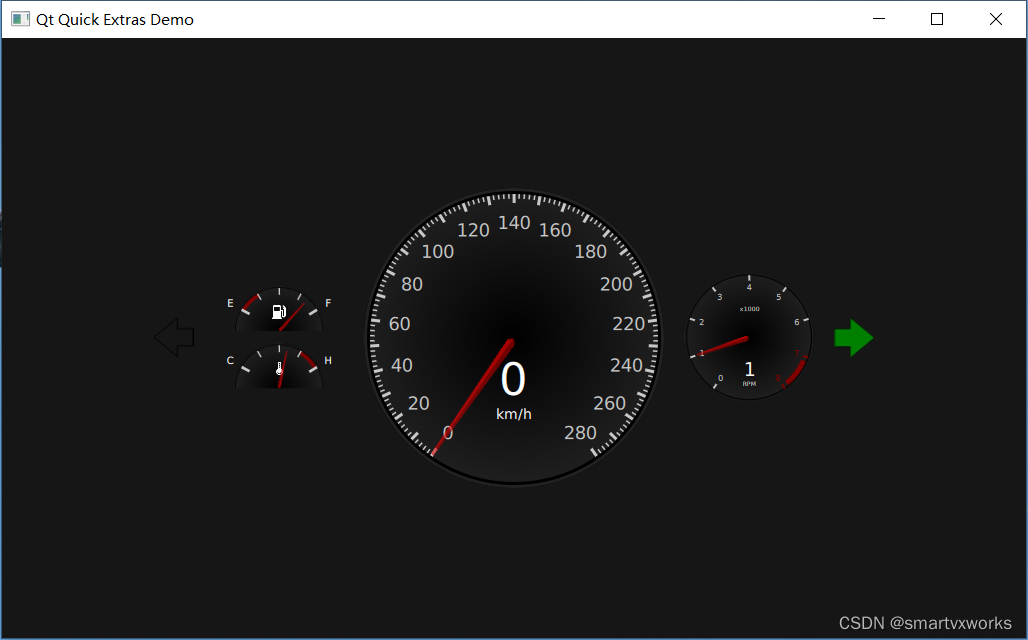
第一个实例:QT实现汽车电子仪表盘
目录 1.实现效果 1.1.视频演示 1.2.实现效果截图 2.生成的安装程序 3.功能概述 4.具体实现 5.QT扩展介绍 5.1.QT介绍 5.2.QT历史发展 5.3.QT平台支持 5.4.Qt Creator 5.5.优势 5.5.1.优良的跨平台特性 5.5.2.面向对象 5.5.3.丰富的 API 1.实现效果 1.1.视频演…...
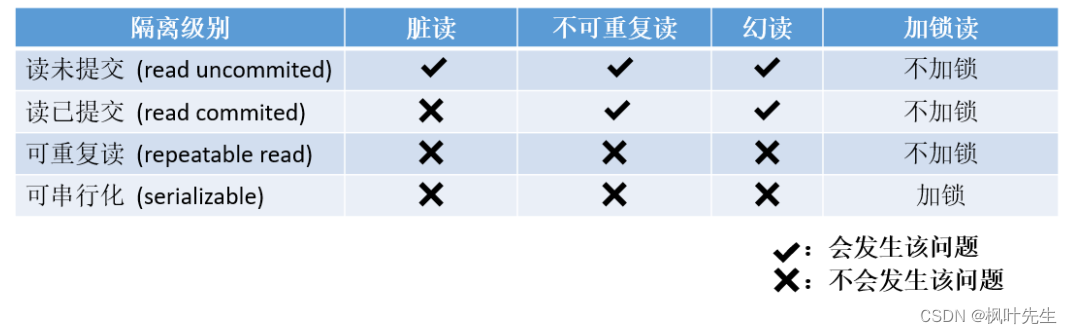
【MySQL系列】MySQL的事务管理的学习(一)_ 事务概念 | 事务操作方式 | 事务隔离级别
「前言」文章内容大致是MySQL事务管理。 「归属专栏」MySQL 「主页链接」个人主页 「笔者」枫叶先生(fy) 目录 一、事务概念二、事务的版本支持三、事务提交方式四、事务常见的操作方式4.1 事务正常操作4.2 事务异常验证 五、事务隔离级别5.1 查看与设置隔离性5.2 读未提交&…...

扫地机器人还能创新吗?云鲸给了个Yes
作者 | 辰纹 来源 | 洞见新研社 1996年,瑞典家电巨头伊莱克斯推出全球首款扫地机器人“三叶虫”。 与现在的产品相比,“三叶虫”靠随机碰撞的模式对空间进行清扫,清洁效率很低,市场渗透率也不高,但并不妨碍戴森、iRo…...
PHP NBA球迷俱乐部系统Dreamweaver开发mysql数据库web结构php编程计算机网页
一、源码特点 PHP NBA球迷俱乐部系统是一套完善的web设计系统,对理解php编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。 基于PHP的NBA球迷俱乐部 二、功能介绍 1、前台主要功能: 系统首页 网站介…...

JavaScript-----DOM元素
目录 前言: 1. DOM介绍 2. 获取节点 3. 操作HTML内容 4. 监听事件 案例 5. 操作节点的标签属性 6. 操作样式 7. 创建、添加、删除节点 前言: 在此之前我们要想去操作网页元素一般是去通过CSS选择器实现的,今天我们就学习JavaScript里…...

激光切割机在船舶行业的的应用有哪些
我国享有世界工厂的美誉,是全球制造业的主力。然而,在船舶制造的关键技术领域,我国的研发投入不足,技术进步仍滞后,我国高端船舶制造的实力仍显不足。 在我国制造业全面复苏的当前背景下,“精准制作”正构成…...
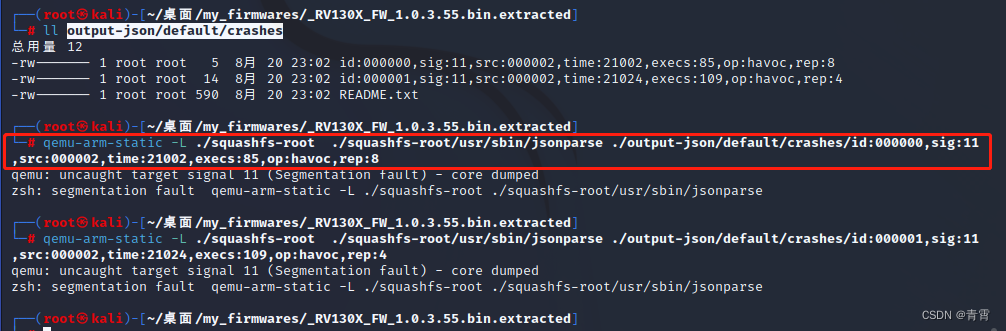
AFL++模糊测试
一、AFL 这里我们主要使用AFL Fuzzing 测试IOT的二进制文件,当我们解压提取一个固件时,能够获得大量的IOT二进制应用 ,如果要进行漏洞挖掘则需要将二进制文件进行逆向分析,然后查找危险函数以及输入接口,对于一个大型的…...

C# 使用ListBox及Picturebox显示所选的任意路径文件夹下的图像
using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System...

数据库: 存储过程
sql server begin end用法: SQL Server中的BEGIN END用法是用于定义一个代码块,这个代码块可以包含多个SQL语句,BEGIN END通常用于控制流程语句,例如IF语句、WHILE语句、TRY CATCH语句等。在BEGIN END代码块中,可以使用变量、函数…...
【juc】ReentrantReadWriteLock之缓存(仅当学习)
目录 一、说明二、代码示例2.1 pom依赖2.2 示例代码2.3 实体类 三、示例截图 一、说明 1.针对于读多写少的情况 2.先查缓存,没有再去查库 二、代码示例 2.1 pom依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"h…...

FLUX查询InfluxDB -- InfluxDB笔记三
1. 入门 from(bucket: "example_query") // 没有筛选条件直接查询会报错|> range(start: -1h) // |>是管道符,后跟筛选条件 2. 序列、表和表流 序列是InfluxDB的概念,一个序列是由measurement、标签集、一个字段名称 表流是FLUX为了…...
pico学习进程记录已经开发项目
Pico pin脚定义 Pico 运行准备 下载uf2文件 https://pico.org.cn/ (注意运行micropython的文件和运行c/c的不一样) 装载uf2文件:按住pico的按键,然后通过micro usb连接电脑(注意:如果用的线材,…...
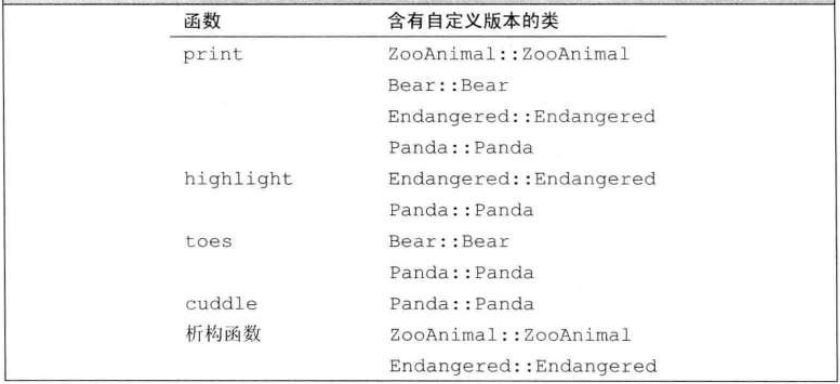
C++(20):多重继承与虚继承
多重继承 是指从多个直接基类中产生派生类的能力。多重继承的派生类继承了所有父类的属性。 多重继承 在派生类的派生列表中可以包含多个基类: class Bear : public zooAnimal { class Panda : public Bear, public Endangered{/* ...*/};每个基类包含一个可选的…...

Vue + Element UI 前端篇(一):搭建开发环境
Vue Element UI 实现权限管理系统 前端篇(一):搭建开发环境 技术基础 开发之前,请先熟悉下面的4个文档 vue.js2.0中文, 优秀的JS框架vue-router, vue.js 配套路由vuex,vue.js 应用状态管理库Element,饿…...

系统错误码指示确立+日志模块手动配置
1,系统错误码指示确立 对于前后端分离的系统设计中,后端建立错误码指示对于前端非常重要可以指示错误存在地方;以用户注册为例; public interface SystemCode{int SYSTEM_USER_ERROR_ADD_FAIL 10000;int SYSTEM_USER_INFO_ADD …...

Java入门第三季
一、异常与异常处理 1. 异常简介 在Java中,**异常是程序在执行过程中出现的问题或意外情况,导致程序无法按照预期的流程进行。**异常处理是Java中用于处理程序中出现的异常的一种机制。 Java中的异常可以分为两大类:受检查的异常ÿ…...

【linux命令讲解大全】056.updatedb命令:创建或更新slocate数据库文件
文章目录 updatedb补充说明语法选项实例 从零学 python updatedb 创建或更新slocate命令所必需的数据库文件 补充说明 updatedb命令用来创建或更新slocate命令所必需的数据库文件。updatedb命令的执行过程较长,因为在执行时它会遍历整个系统的目录树,…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...
