「TCG 规范解读」第11章 TPM工作组 TCG算法注册表
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alliance,TCPA)所开发的规范。现在的规范都不是最终稿,都还在不断的更新中,比如:TPM的规范就从原来的v1.0更新到v1.2,现在还在不断的修订。
TCG-_Algorithm_Registry_r1p32_pub
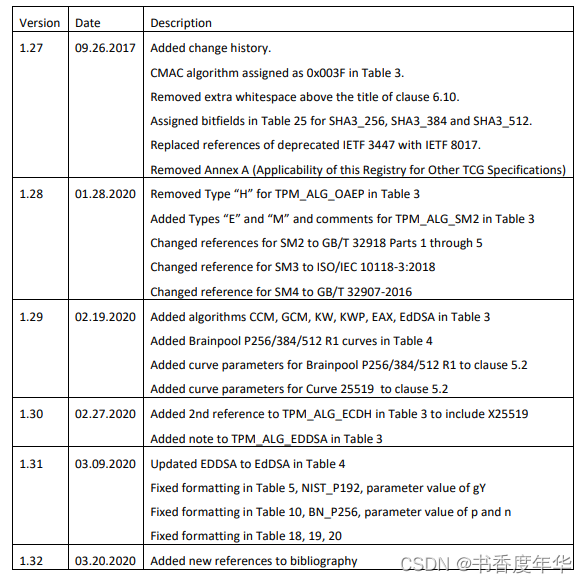
修订历史
TPM_ALG_ID
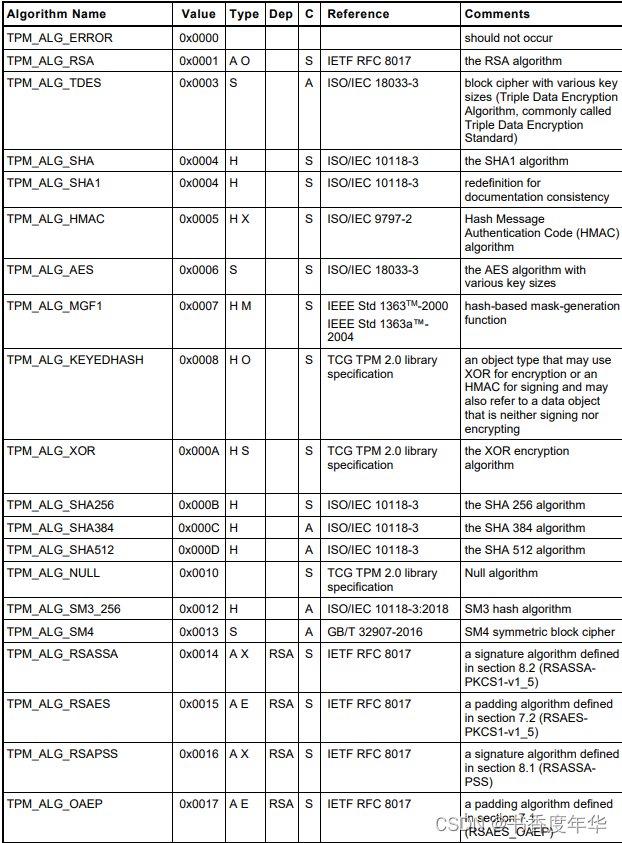
表3 是 TCG 给各个算法分配的标识,这些 ID 可用用来区分算法上下文中的数据结构,合法 ID 的取值范围是 0x0000~0x7fff,0x8000 以上用做 TCG 规定的其他的标签值。
这些算法包含了 RSA、TDES、SHA、HMAC、AES、SM3、SM4、ECC、KDF等,看起来是非常丰富的算法支持。其中 SM3、SM4 是国密算法,这也是 TPM 2.0 中引入的支持。
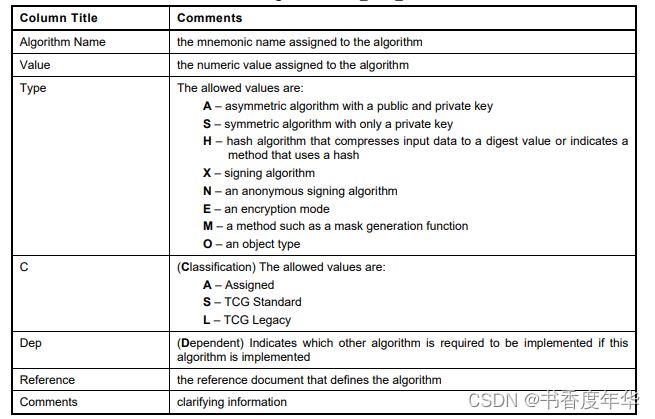
从表2中我们可以看到算法名称、表示的数值、算法类型、依赖、类别、参考以及备注。
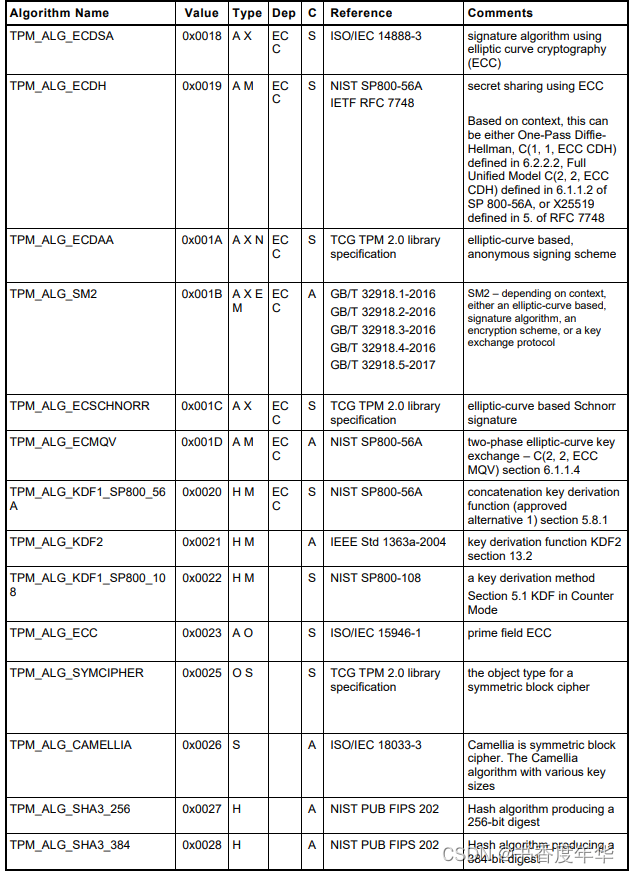
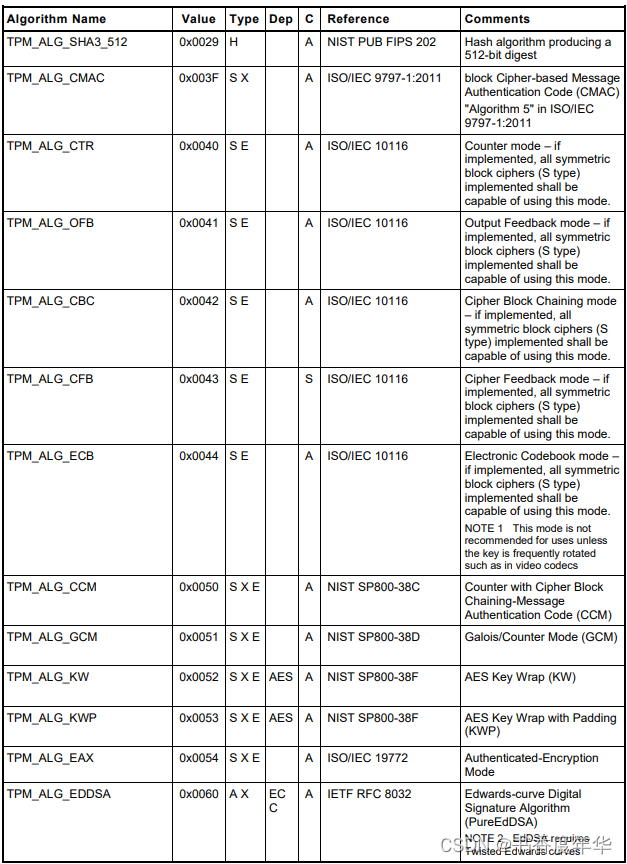
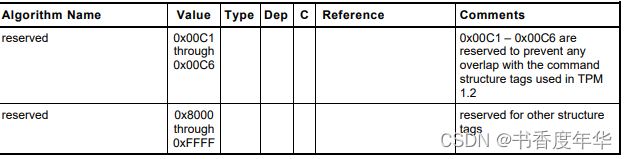
ECC相关数值
算法 ID
表 5 列出了 TCG 注册的 ECC 算法的 ID,可以看出对于 ECC 的支持也是比较全面的,包含了NIST 系列曲线、BN 曲线、SM2 曲线、BP 曲线、25519 曲线。
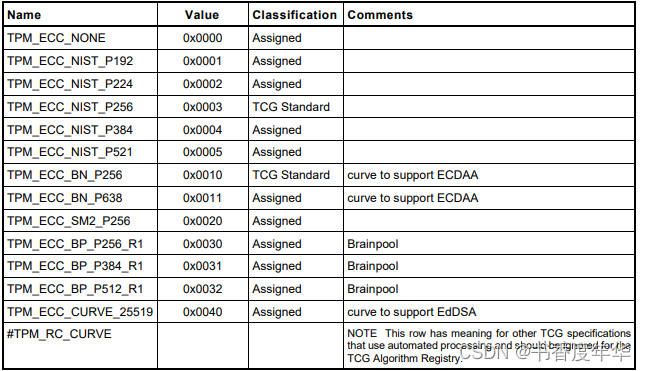
曲线参数
这节主要描述了图 5 中描述 ECC 算法的相关参数,具体如下:
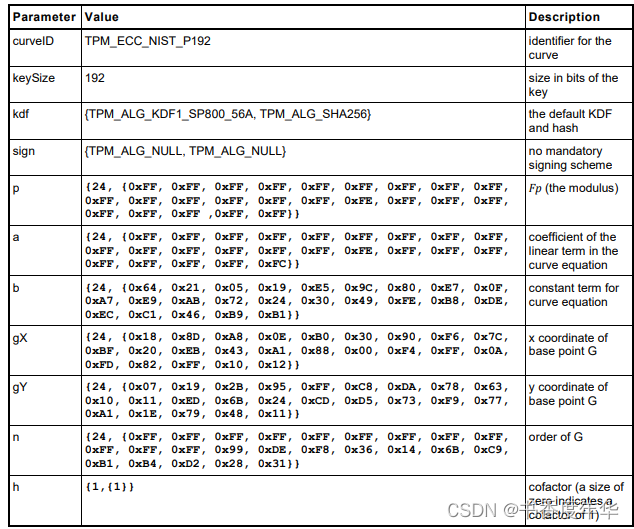
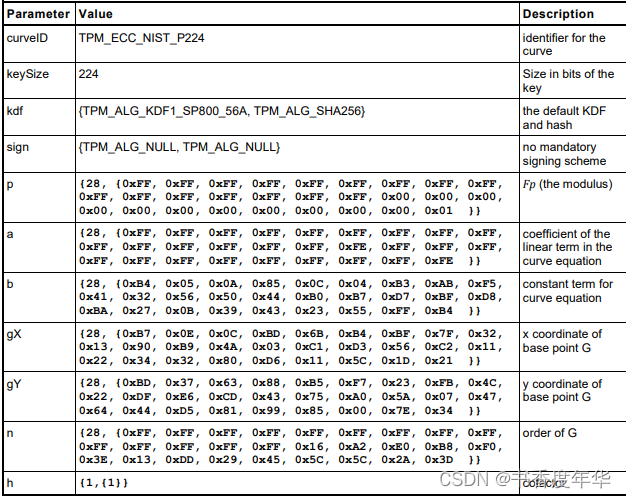
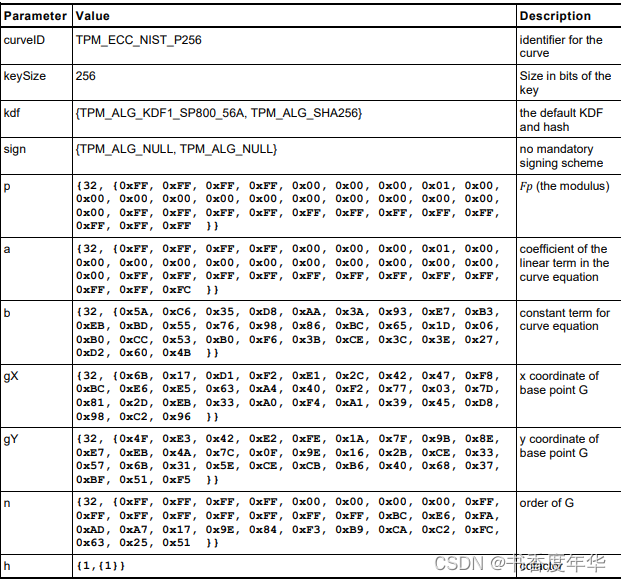
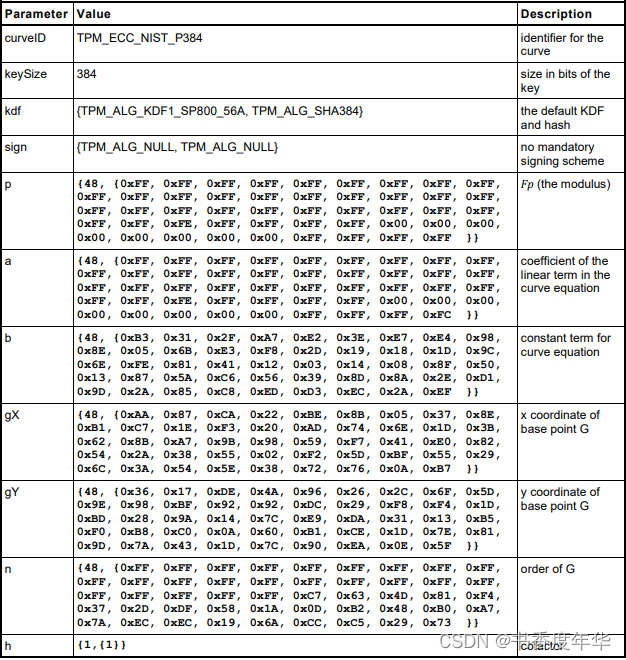
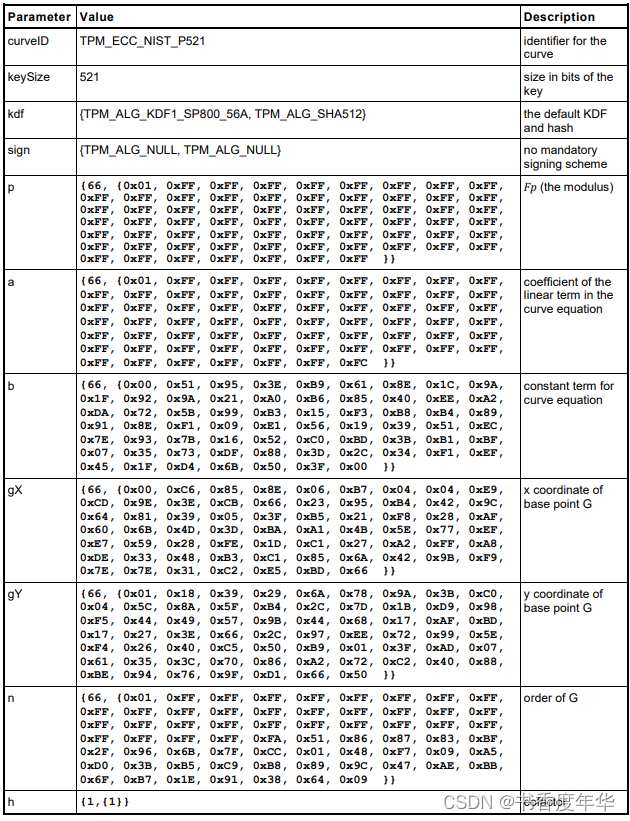
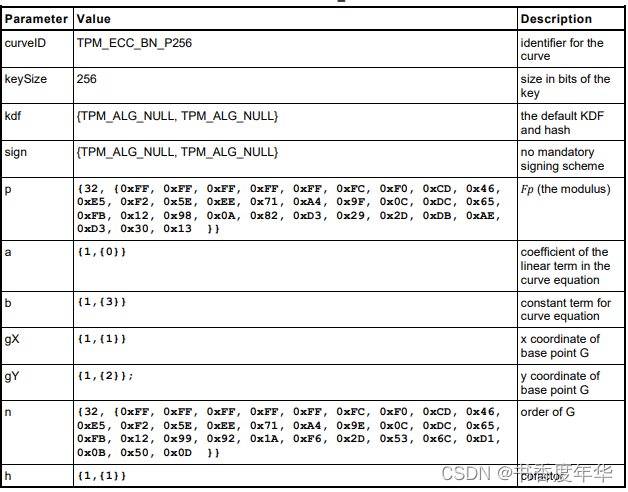
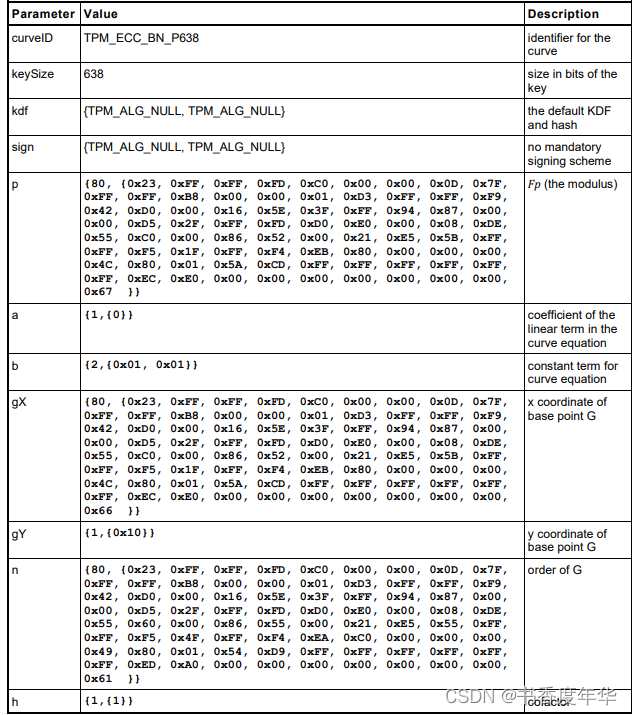
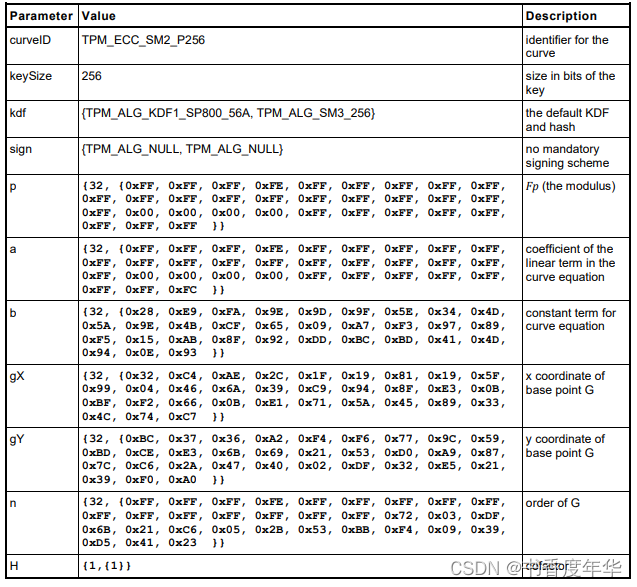
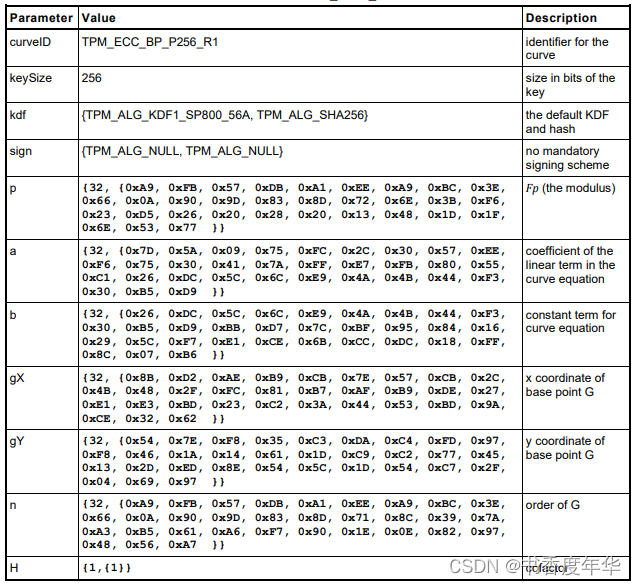
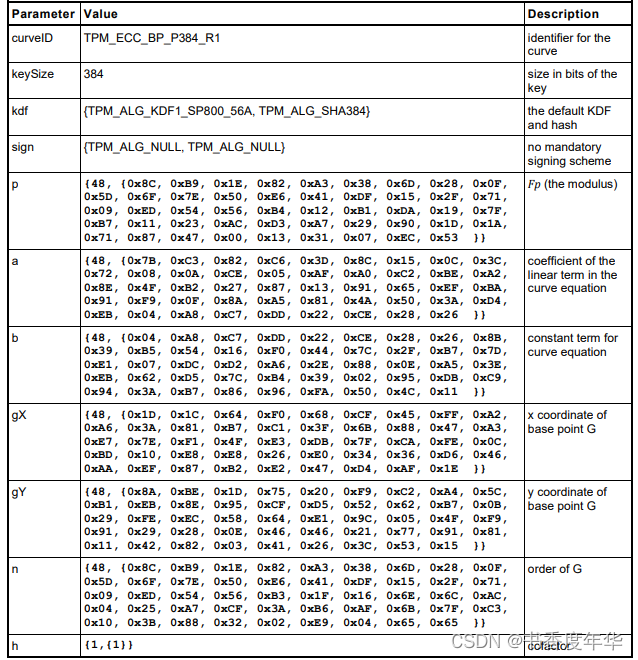
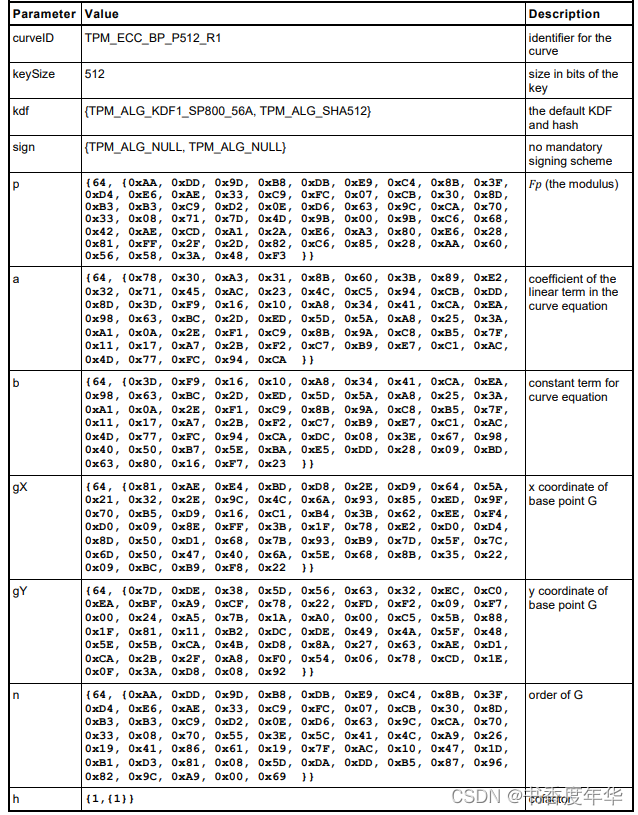
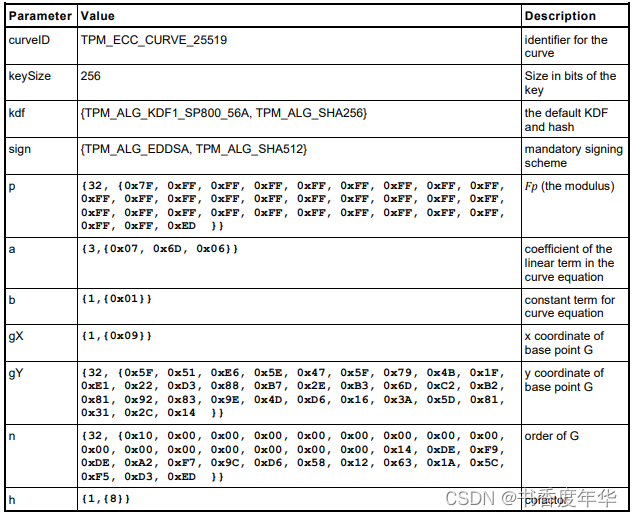
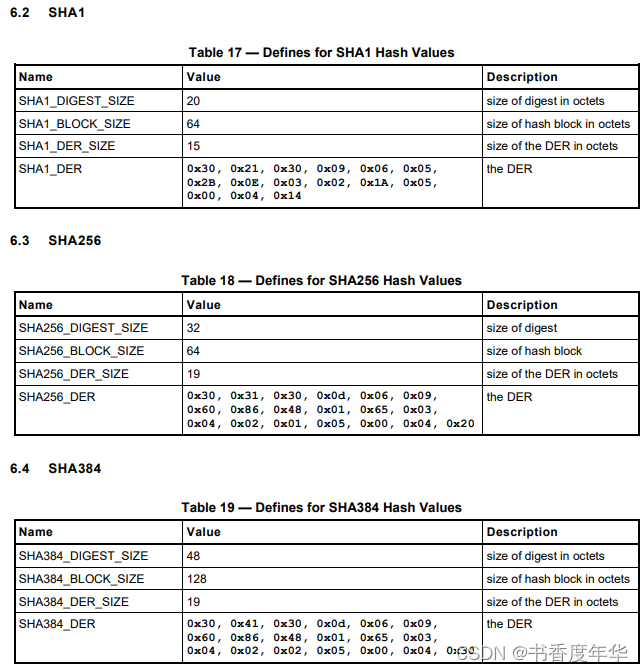
哈希参数
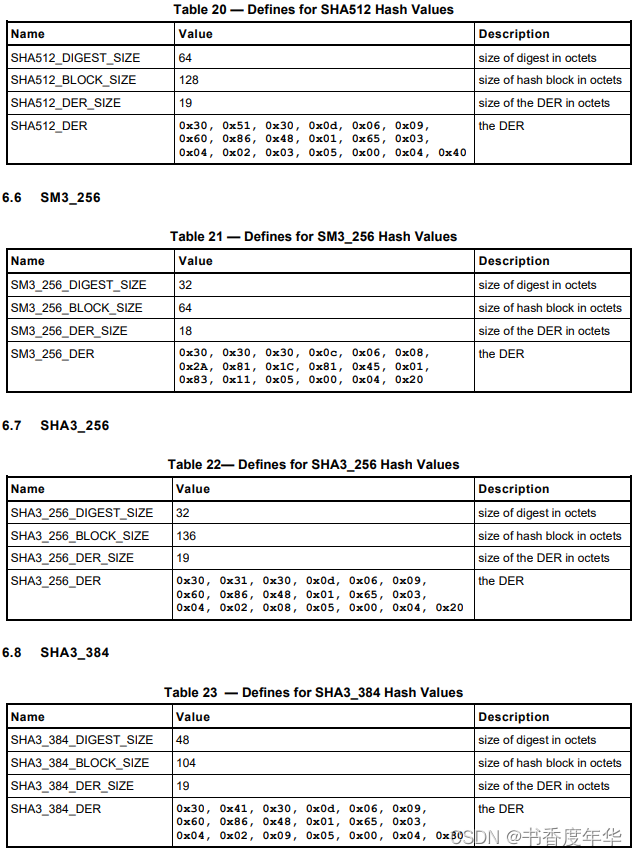

对称加密参数
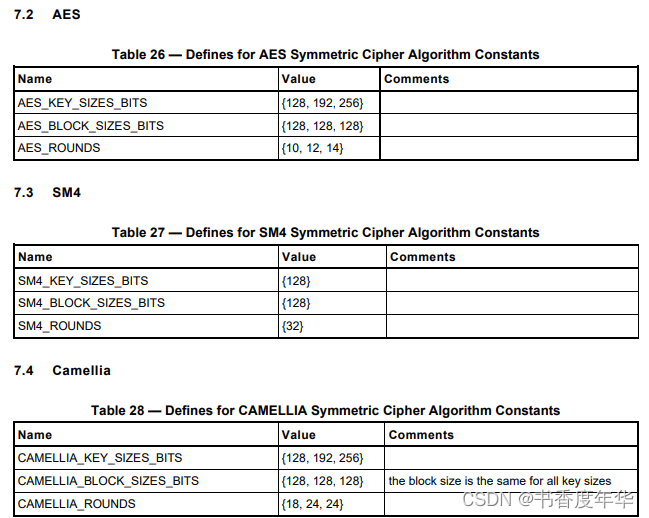
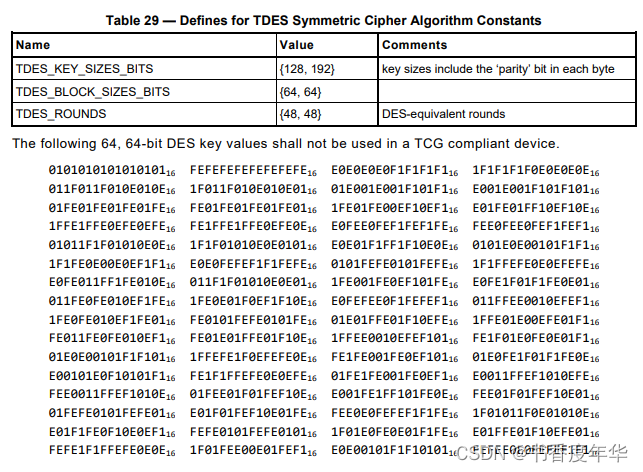
参考
• FIPS 202, SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions
• GB/T 32907-2016: Information security technology—SM4 block cipher algorithm
• GB/T 32918.1-2016: Information security technology—Public key cryptographic algorithm SM2 based on elliptic curves—Part 1: General
• GB/T 32918.2-2016: Information security technology—Public key cryptographic algorithm SM2 based on elliptic curves—Part 2: Digital signature algorithm
• GB/T 32918.3-2016: Information security technology—Public key cryptographic algorithm SM2 based on elliptic curves—Part 3: Key exchange protocol
• GB/T 32918.4-2016: Information security technology—Public key cryptographic algorithm SM2 based on elliptic curves—Part 4: Public key encryption algorithm
• GB/T 32918.5-2017: Information security technology—Public key cryptographic algorithm SM2 based on elliptic curves—Part 5: Parameter definition
• IEEE Std 1363TM-2000, Standard Specifications for Public Key Cryptography
• IEEE Std 1363a™-2004 (Amendment to IEEE Std 1363™-2000), IEEE Standard Specifications for Public Key Cryptography- Amendment 1: Additional Techniques
• IETF RFC 8017, Public-Key Cryptography Standards (PKCS) #1: RSA Cryptography Specifications Version 2.2
• IETF RFC 7748, Elliptic Curves for Security • IETF RFC 8032, Edwards-Curve Digital Signature Algorithm (EdDSA)
• ISO/IEC 9797-2, Information technology — Security techniques — Message authentication codes (MACs) — Part 2: Mechanisms using a dedicated hash-function
• ISO/IEC 10116, Information technology — Security techniques — Modes of operation for an nbit block cipher
• ISO/IEC 10118-3, Information technology — Security techniques — Hash-functions — Part 3: Dedicated hash functions
• ISO/IEC 14888-3, Information technology -- Security techniques -- Digital signature with appendix -- Part 3: Discrete logarithm based mechanisms
• ISO/IEC 15946-1, Information technology — Security techniques — Cryptographic techniques based on elliptic curves — Part 1: General
• ISO/IEC 18033-3, Information technology — Security techniques — Encryption algorithms — Part 3: Block ciphers
• ISO/IEC 19772, Information technology — Security techniques — Authenticated encryption • NIST SP800-108, Recommendation for Key Derivation Using Pseudorandom Functions (Revised)
• NIST SP800-56A, Recommendation for Pair-Wise Key Establishment Schemes Using Discrete Logarithm Cryptography (Revised)
• NIST SP800-38C, Recommendation for Block Cipher Modes of Operation: The CCM Mode for Authentication and Confidentiality
• NIST SP800-38D, Recommendation for Block Cipher Modes of Operation: Galois/Counter Mode (GCM) and GMAC
术语
TCG,可信计算组织;
TPM,可信平台模块;
可信度量,主体通过密码学方法对客体进行度量的方法;
皮格马利翁效应心理学指出,赞美、赞同能够产生奇迹,越具体,效果越好~
“收藏夹吃灰”是学“器”练“术”非常聪明的方法,帮助我们避免日常低效的勤奋~
相关文章:

「TCG 规范解读」第11章 TPM工作组 TCG算法注册表
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...

华为OD机试 - 事件推送(C++) | 附带编码思路 【2023】
刷算法题之前必看 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单查看地址:https://blog.csdn.net/hihell/category_12199283.html 华为OD详细说明:https://dream.blog.csdn.net/article/details/128980730 华为OD机试题…...

Java ”框架 = 注解 + 反射 + 设计模式“ 之 注解详解
Java ”框架 注解 反射 设计模式“ 之 注解详解 每博一文案 刹那间我真想令时光停住,好让我回顾自己,回顾失去的年华,缅怀哪个穿一身短小的连衣裙 和瘦窄的短衫的小女孩。让我追悔少年时代,我心灵的愚钝无知,它轻易…...
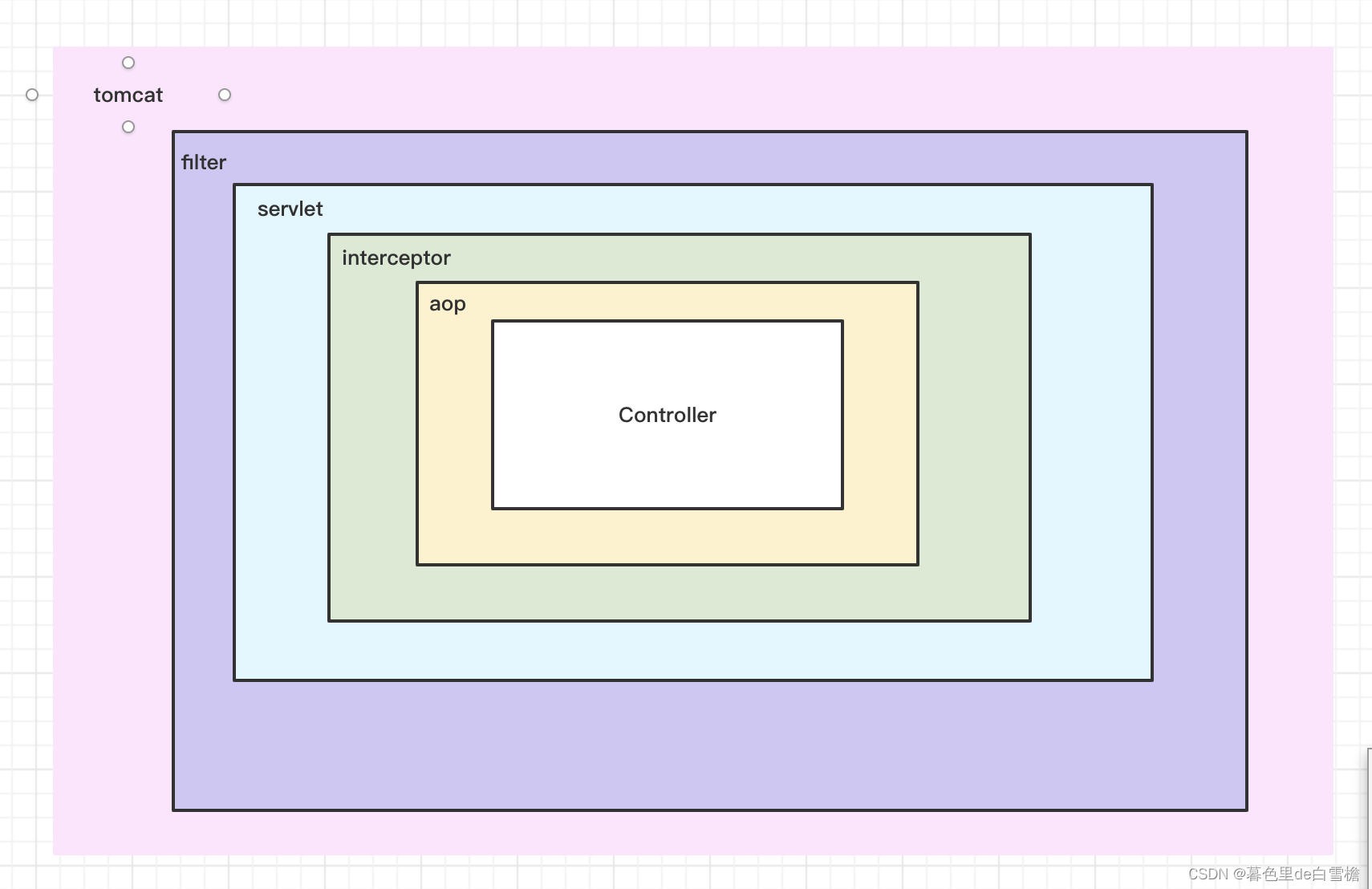
【拦截器、过滤器、springAop】那些不为人知的隐秘
首先说到这几个词的时候,大家肯定都很熟悉了,甚至觉得这几个的区别刚刚毕业都能回答了,但是我想大家在实际应用过程中是真得会真正的使用吗?换言之,什么时候用过滤器什么时候使用拦截器,什么时候使用spring…...

记录charles手机端配置https的成功过程
1.百度 https://www.likecs.com/show-204025787.html https://blog.csdn.net/enthan809882/article/details/117572094?spm1001.2101.3001.6650.6&utm_mediumdistribute.pc_relevant.none-task-blog-2defaultBlogCommendFromBaiduRate-6-117572094-blog-122959902.pc_rele…...
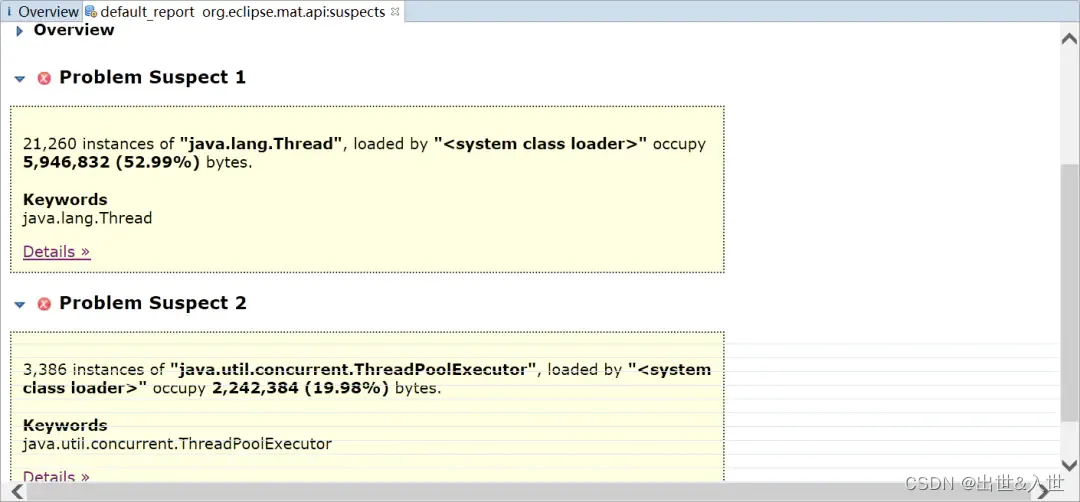
你知道这几种常见的JVM调优场景吗?
看此文前需已了解了运行时的数据区域和常用的垃圾回收算法,也了解了Hotspot支持的垃圾回收器。 一、cpu占用过高 cpu占用过高要分情况讨论,是不是业务上在搞活动,突然有大批的流量进来,而且活动结束后cpu占用率就下降了…...
)
华为OD机试真题Python实现【最长连续子串】真题+解题思路+代码(20222023)
最长连续子串 题目 给定一个字符串 只包含字母和数字 按要求找出字符串中的最长连续子串的长度 字符串本身是其最长的子串 子串要求 只包含一个字母(a~z A~Z)其余必须是数字字母可以在子串中的任意位置 如果找不到满足要求的子串 比如说,全是字母或数字则返回-1 🔥🔥🔥…...
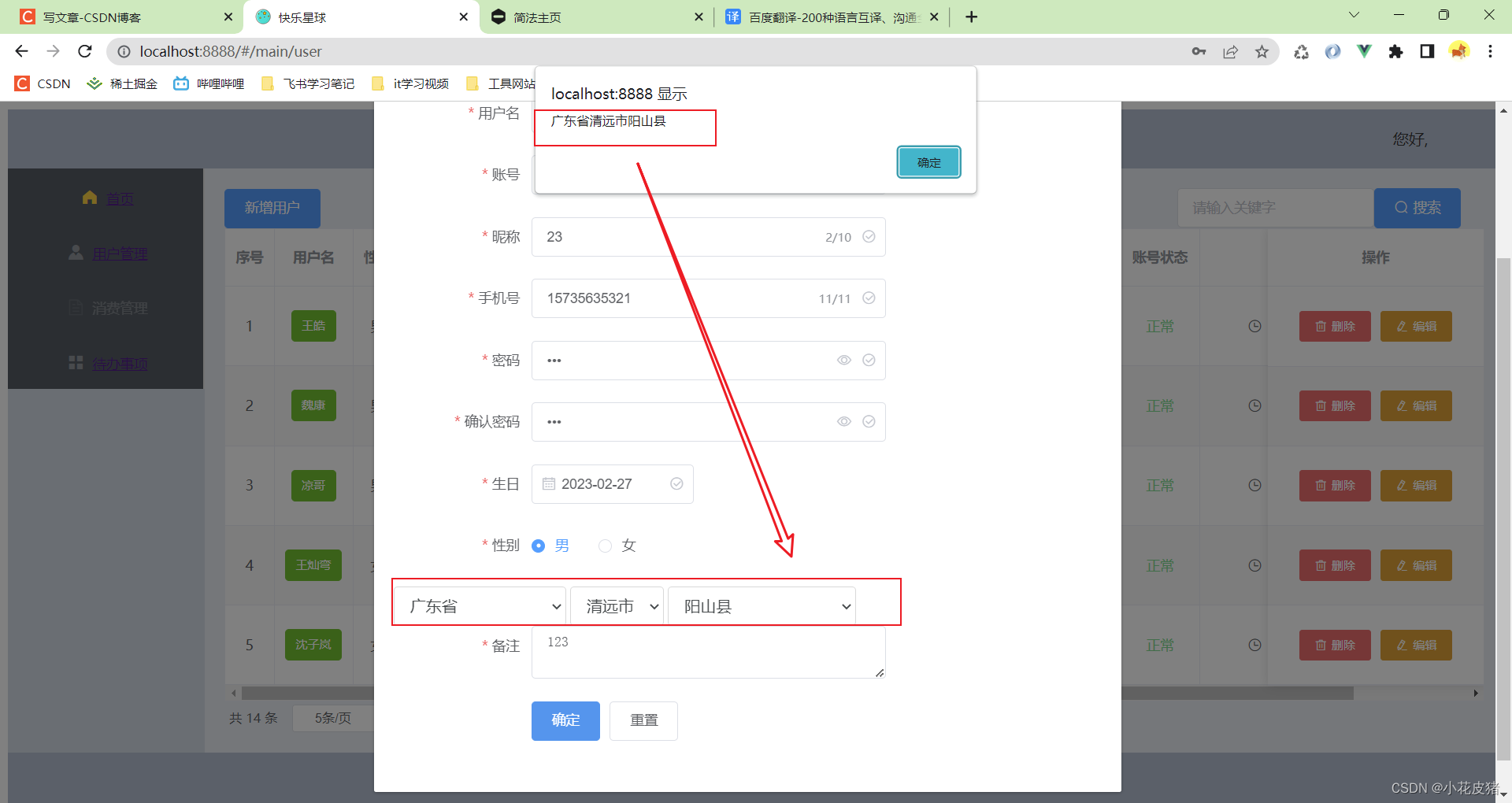
Vue使用distpicker插件实现省市级下拉框三级联动
前言 这几天做项目,想着用一个全国省市区插件,之前就知道有几种,比如通过JSON文件生成对应的区域下拉框,element-china-are插件,包括distpicker插件 今天主要介绍的是如何使用distpicker插件实现省市级三联跳动 官网…...

Unity Avatar Foot IK - Avatar Foot Placement Resolution
文章目录简介实现Avatar FBX Import SettingsAnimator SettingsOn Animator IKCalculate IK Position & RotationBody PositionApply IK Position & Rotation简介 通过Unity内部的Mecanim动画系统实现的FootIK功能,效果如图所示,左右分别为开启…...

是时候告别这些 Python 库了
随着每个 Python 版本的发布,都会添加新模块,并引入新的更好的做事方式,虽然我们都习惯了使用好的旧 Python 库和某些做事方式,但现在也时候升级并利用新的和改进的模块及其特性了。 文章目录技术提升PathlibSecretsZoneinfoDatac…...

nodejs基于vue论坛交流管理系统
可定制框架:ssm/Springboot/vue/python/PHP/小程序/安卓均可开发目录 目录 1 绪论 1 1.1课题背景 1 1.2课题研究现状 1 1.3初步设计方法与实施方案 2 1.4本文研究内容 2 2 系统开发环境 4 3 系统分析 6 3.1系统可行性分析 6 3.1.1经济可行性 6 3.1.2技术可行性 6 3.1.3运行可行…...
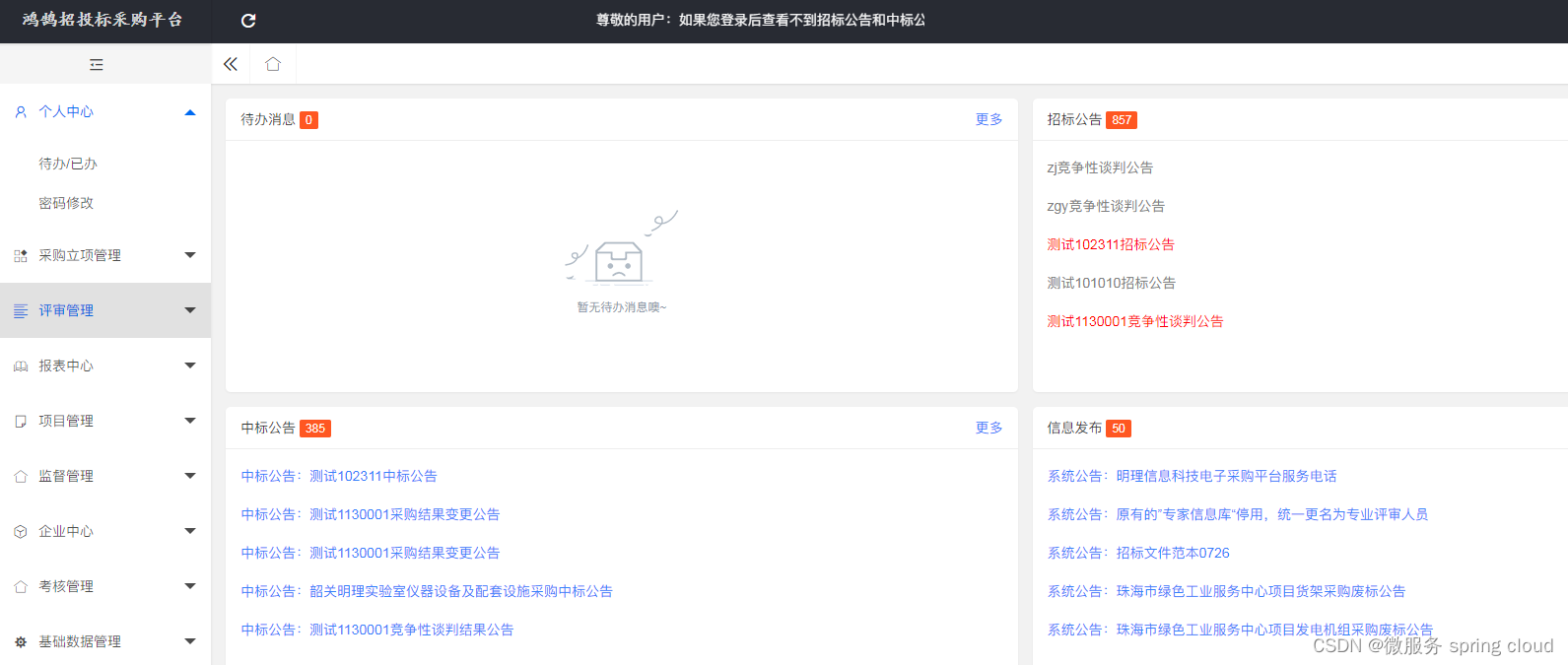
企业电子招投标采购系统源码之系统的首页设计
功能模块: 待办消息,招标公告,中标公告,信息发布 描述: 全过程数字化采购管理,打造从供应商管理到采购招投标、采购合同、采购执行的全过程数字化管理。通供应商门户具备内外协同的能力,为…...
)
华为OD机试真题Python实现【竖直四子棋】真题+解题思路+代码(20222023)
竖直四子棋 题目 竖直四子棋的棋盘是竖立起来的,双方轮流选择棋盘的一列下子, 棋子因重力落到棋盘底部或者其他棋子之上,当一列的棋子放满时,无法再在这列上下子。 一方的4个棋子横、竖或者斜方向连成一线时获胜。 现给定一个棋盘和红蓝对弈双方的下子步骤,判断红方或蓝…...

LeetCode 73. 矩阵置零
LeetCode 73. 矩阵置零 难度:middle\color{orange}{middle}middle 题目描述 给定一个 KaTeX parse error: Double subscript at position 3: _m_̲ x _n_ 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法…...
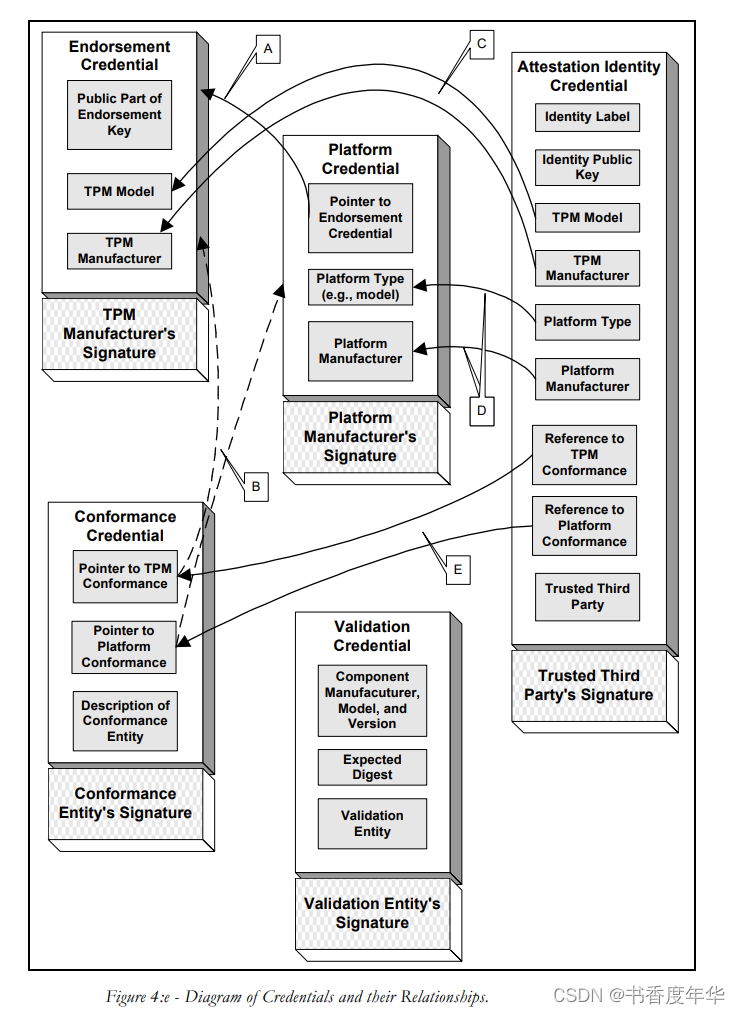
「TCG 规范解读」第10章 TPM工作组 保护你的数字环境
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...
)
华为OD机试真题Python实现【 找字符】真题+解题思路+代码(20222023)
找字符 题目 给定两个字符串, 从字符串2中找出字符串1中的所有字符, 去重并按照 ASCII 码值从小到大排列。 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 ## 输入 字符范围满足 ASCII 编码要求, 输入字符串1长度不超过1024, 字符串…...
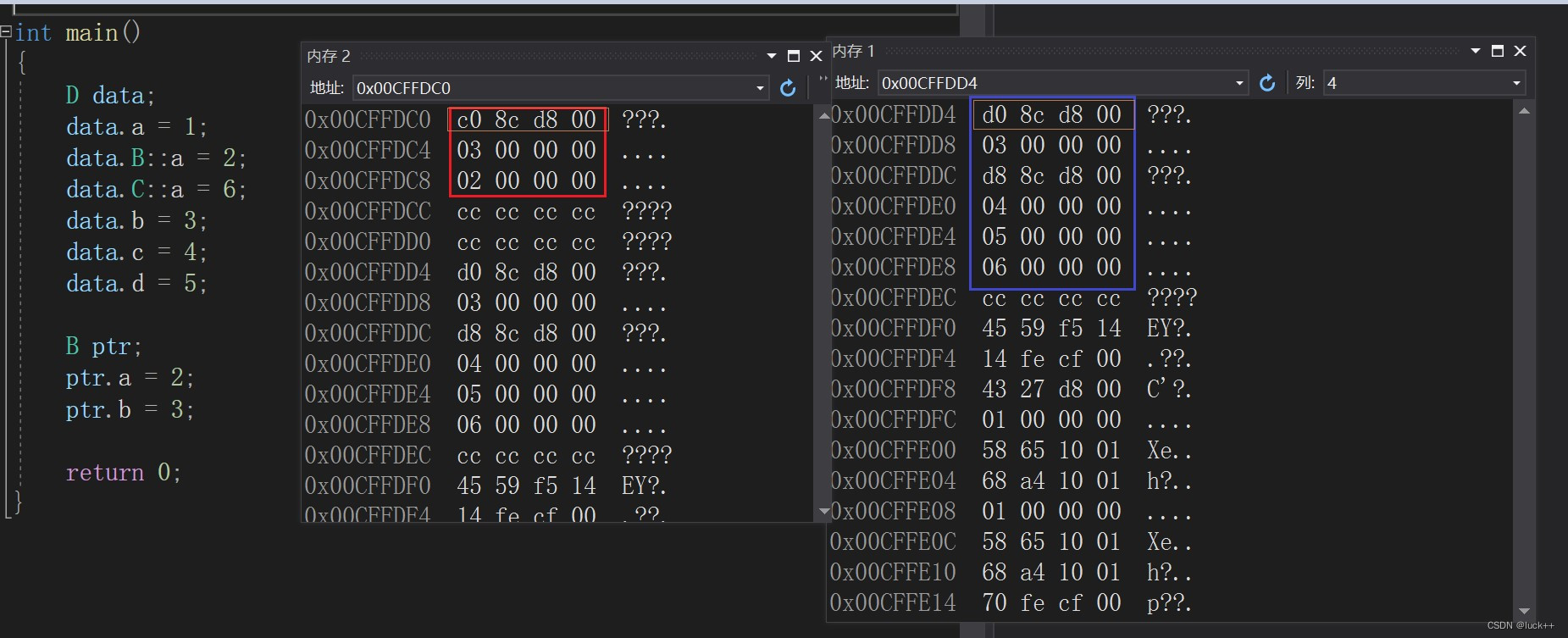
如何解决多继承下的 菱形继承 问题
目录 概念: 菱形虚拟继承: 概念: 此时D类属于多继承,可以看到D类里面会有两份A类的数据,菱形继承也并不一定就一定就是上图的菱形,假如B类下面还有一个类,D类继承它,同样也是菱形继承问题 cla…...

rk3288-android8.1-以太网ethernet和蓝牙Bluetooth
遇到一个现象,以太网和蓝牙打不开 经过不断分析和查找发现问题在.config中 CONFIG_MOTORCOMM_PHYy 会导致以太网的eth0注册不成功(现在是双网口,还有个USB网卡) 改成# CONFIG_MOTORCOMM_PHY is not set 后以太网可以正常 # CONFIG_RTC_DRV_RK808 is not set 会导致蓝牙打不…...

算法比赛——必备的数论知识
秋名山码民的主页 🎉欢迎关注🔎点赞👍收藏⭐️留言📝 🙏作者水平有限,如发现错误,还请私信或者评论区留言! 目录一、欧几里得二、扩展欧几里得三、算术基本定理四、线性筛选求质数五…...
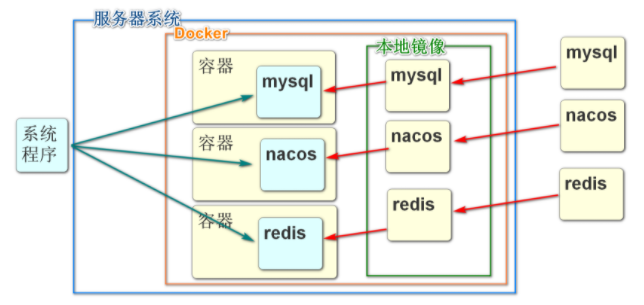
Docker概述
什么是Docker我们要学习在Linux(RockyLinux)中安装使用Docker来配置软件的功能Docker是一个用来开发、运输和运行应用程序的开放平台。使用Docker可以将应用程序与基础结构分离,以便快速交付软件。使用Docker,您可以以管理应用程序的方式管理基础架构。通…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...
