LeetCode 73. 矩阵置零
LeetCode 73. 矩阵置零
难度:middle\color{orange}{middle}middle
题目描述
给定一个 KaTeX parse error: Double subscript at position 3: _m_̲ x _n_ 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法 。
示例 1:
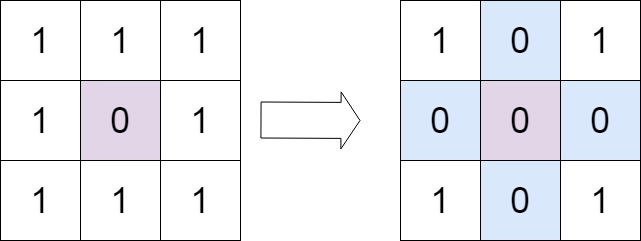
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FZihipLq-1677032011375)(null)]](https://img-blog.csdnimg.cn/bb15b9f7948a48f88f713dbbeca1cfd1.png)
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
- m==matrix.lengthm == matrix.lengthm==matrix.length
- n==matrix[0].lengthn == matrix[0].lengthn==matrix[0].length
- 1<=m,n<=2001 <= m, n <= 2001<=m,n<=200
- −231<=matrix[i][j]<=231−1-2^{31} <= matrix[i][j] <= 2^{31} - 1−231<=matrix[i][j]<=231−1
进阶:
- 一个直观的解决方案是使用 O(mn)O(mn)O(mn) 的额外空间,但这并不是一个好的解决方案。
- 一个简单的改进方案是使用 O(m+n)O(m+ n)O(m+n) 的额外空间,但这仍然不是最好的解决方案。
- 你能想出一个仅使用常量空间的解决方案吗?
算法
(原地算法) O(nm)O(nm)O(nm)
我们只需统计出矩阵中每一行或者每一列是否有0,然后把含有0的行或者列都置成0即可。
- 用两个变量记录第一行和第一列是否有0。
- 遍历整个矩阵,用矩阵的第一行和第一列记录对应的行和列是否有0。
- 把含有0的行和列都置成0。
复杂度分析
-
时间复杂度:矩阵中每个元素只遍历常数次数,所以时间复杂度是O(nm)O(nm)O(nm)。
-
空间复杂度 : 只用了两个额外的变量记录第一行和第一列是否含有0,所以额外的空间复杂度是 O(1)O(1)O(1)。
C++ 代码
class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {if (matrix.empty()) return;int n = matrix.size(), m = matrix[0].size();int r0 = 1, c0 = 1;//判断第0行for (int i = 0; i < m; i ++) if (matrix[0][i] == 0) r0 = 0;//判断第0列for (int i = 0; i < n; i ++) if (matrix[i][0] == 0) c0 = 0;//判断第1行到第n - 1行是否有0,存储在第一列中for (int i = 1; i < n; i ++) {for (int j = 0; j < m; j ++) {if (matrix[i][j] == 0) matrix[i][0] = 0;}}//判断第1列到第 n - 1列是否有0,存储在第一行中for (int i = 1; i < m; i ++) {for (int j = 0; j < n; j ++) {if (matrix[j][i] == 0) matrix[0][i] = 0;}}// 修改行的数值for (int i = 1; i < n; i ++ ) {if (matrix[i][0] == 0) for (int j = 0; j < m; j ++) matrix[i][j] = 0;}//修改列的数值for (int i = 1; i < m; i ++) {if (matrix[0][i] == 0) for (int j = 0; j < n; j ++)matrix[j][i] = 0;}//修改第一行if (r0 == 0) for (int i = 0; i < m; i ++) matrix[0][i] = 0;//修改第一列if (c0 == 0) for (int i = 0; i < n; i ++) matrix[i][0] = 0;}
};
相关文章:

LeetCode 73. 矩阵置零
LeetCode 73. 矩阵置零 难度:middle\color{orange}{middle}middle 题目描述 给定一个 KaTeX parse error: Double subscript at position 3: _m_̲ x _n_ 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法…...
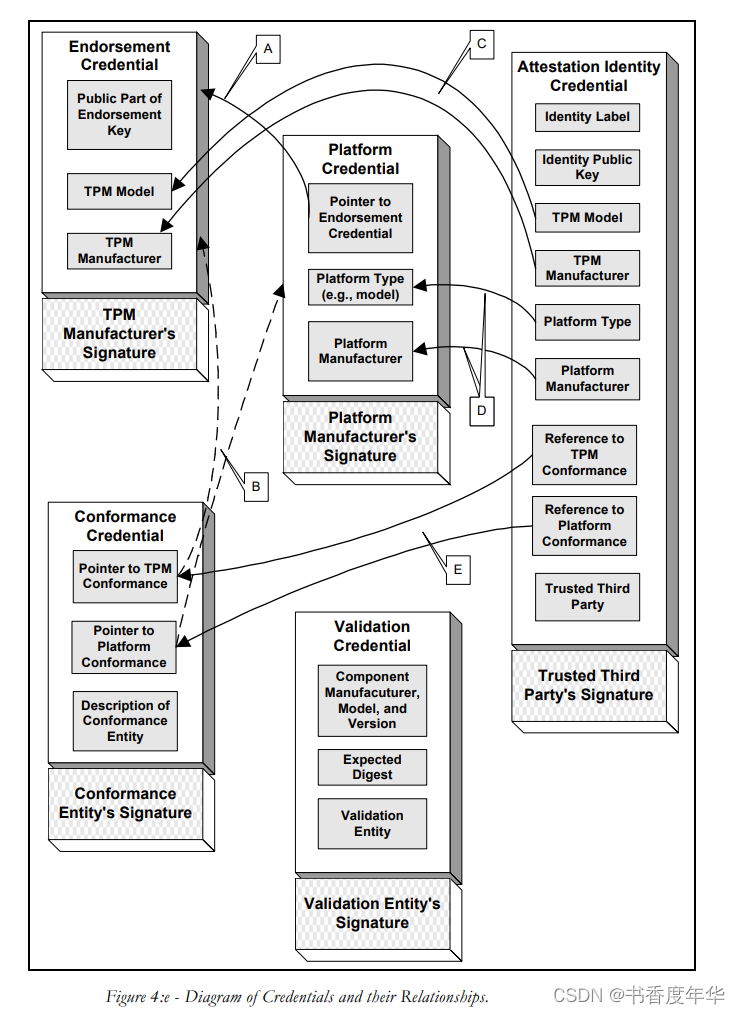
「TCG 规范解读」第10章 TPM工作组 保护你的数字环境
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...
)
华为OD机试真题Python实现【 找字符】真题+解题思路+代码(20222023)
找字符 题目 给定两个字符串, 从字符串2中找出字符串1中的所有字符, 去重并按照 ASCII 码值从小到大排列。 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 ## 输入 字符范围满足 ASCII 编码要求, 输入字符串1长度不超过1024, 字符串…...
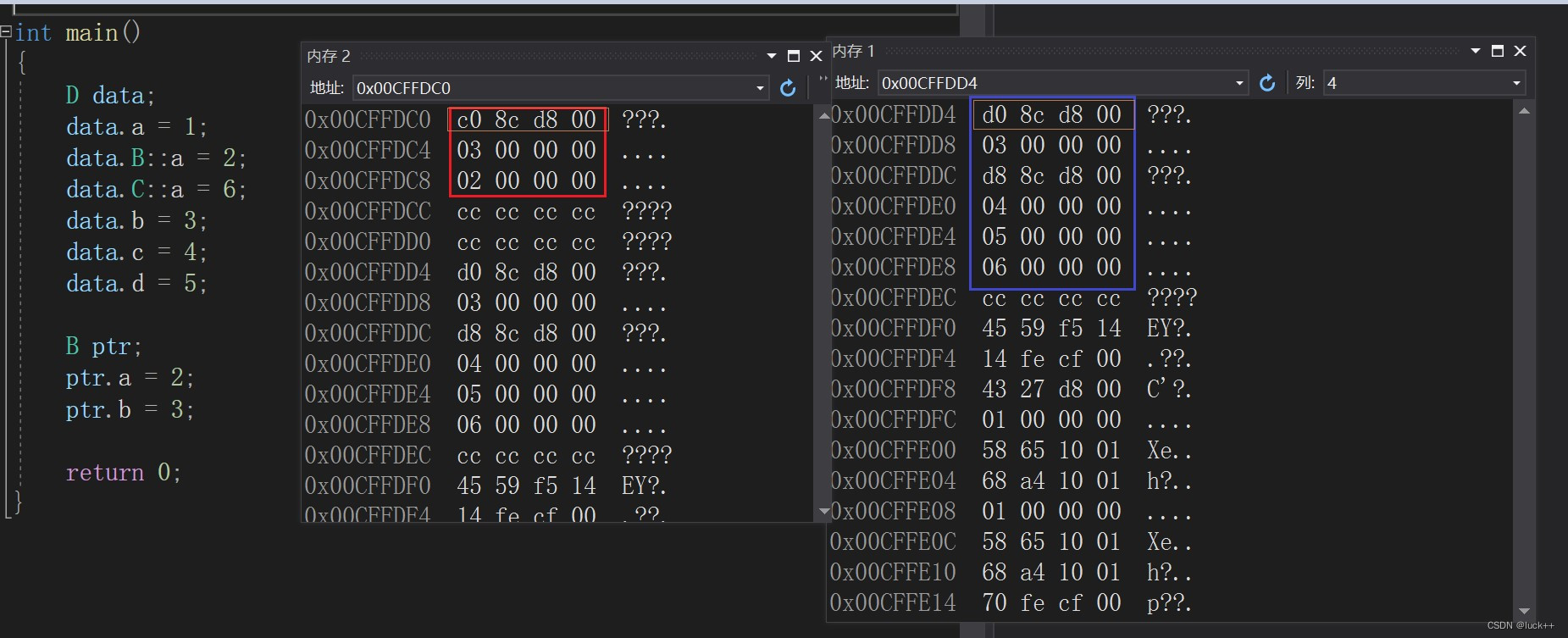
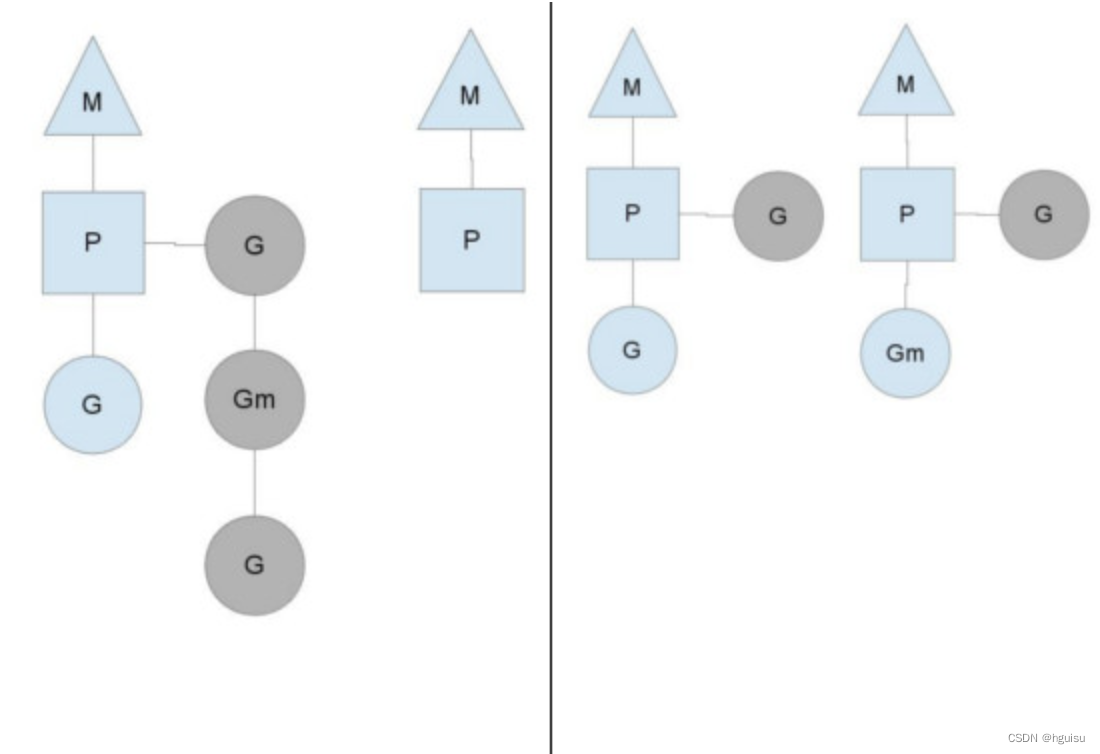
如何解决多继承下的 菱形继承 问题
目录 概念: 菱形虚拟继承: 概念: 此时D类属于多继承,可以看到D类里面会有两份A类的数据,菱形继承也并不一定就一定就是上图的菱形,假如B类下面还有一个类,D类继承它,同样也是菱形继承问题 cla…...

rk3288-android8.1-以太网ethernet和蓝牙Bluetooth
遇到一个现象,以太网和蓝牙打不开 经过不断分析和查找发现问题在.config中 CONFIG_MOTORCOMM_PHYy 会导致以太网的eth0注册不成功(现在是双网口,还有个USB网卡) 改成# CONFIG_MOTORCOMM_PHY is not set 后以太网可以正常 # CONFIG_RTC_DRV_RK808 is not set 会导致蓝牙打不…...

算法比赛——必备的数论知识
秋名山码民的主页 🎉欢迎关注🔎点赞👍收藏⭐️留言📝 🙏作者水平有限,如发现错误,还请私信或者评论区留言! 目录一、欧几里得二、扩展欧几里得三、算术基本定理四、线性筛选求质数五…...
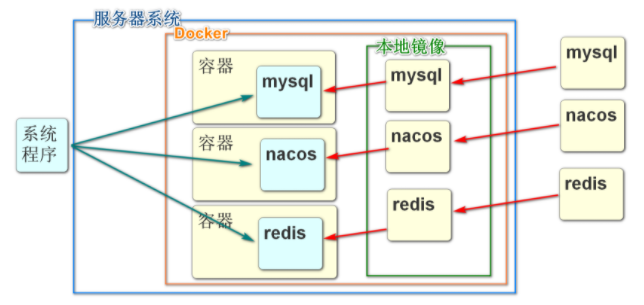
Docker概述
什么是Docker我们要学习在Linux(RockyLinux)中安装使用Docker来配置软件的功能Docker是一个用来开发、运输和运行应用程序的开放平台。使用Docker可以将应用程序与基础结构分离,以便快速交付软件。使用Docker,您可以以管理应用程序的方式管理基础架构。通…...

实验室设计建设方案主要内容
实验室设计建设整体解决方案SICOLAB需要综合考虑实验室的功能需求、空间布局、设备选型、安全防护、节能环保等多方面因素。以下是一个基本的实验室设计建设方案的流程:一、需求分析:了解实验室的使用目的、实验内容、使用人数、设备种类、实验标准等&am…...
)
华为OD机试真题Python实现【日志采集系统】真题+解题思路+代码(20222023)
日志采集系统 题目 日志采集是运维系统的的核心组件。日志是按行生成,每行记做一条,由采集系统分批上报。 如果上报太频繁,会对服务端造成压力; 如果上报太晚,会降低用户的体验; 如果一次上报的条数太多,会导致超时失败。 为此,项目组设计了如下的上报策略: 每成功上…...

Python的模块与工具包
模块 模块是一个Python文件,以 .py结尾。模块能定义函数,类和变量,模块里也能包含可执行的代码。 作用 python 中有很多各种不同的模块,每一个模块都可以帮助我们快速的实现一些功能,比如实现和时间相关的功能就可以…...

联合熵和条件熵
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。 文章目录联合熵条件熵联合…...
)
华为OD机试真题Python实现【求最大数字】真题+解题思路+代码(20222023)
求最大数字 题目 给定一个由纯数字组成以字符串表示的数值,现要求字符串中的每个数字最多只能出现2次,超过的需要进行删除;删除某个重复的数字后,其它数字相对位置保持不变。 如34533,数字3重复超过2次,需要删除其中一个3,删除第一个3后获得最大数值4533 请返回经过删…...

Python爬虫(10)selenium爬虫后数据,存入csv、txt并将存入数据并对数据进行查询
之前的文章有关于更多操作方式详细解答,本篇基于前面的知识点进行操作,如果不了解可以先看之前的文章 Python爬虫(1)一次性搞定Selenium(新版)8种find_element元素定位方式 Python爬虫(2)-Selenium控制浏览…...
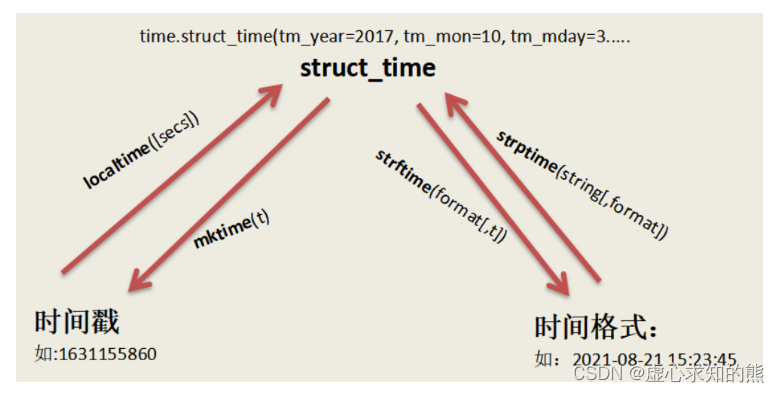
Python 之 Pandas 时间函数 time 、datetime 模块和时间处理基础
文章目录一、time 模块1、时间格式转换图2. struct_time 元组元素结构3. format time 结构化表示二、datetime 模块1. date类2. 方法和属性3. datetime 类三、timedelta 类的时间加减四、时间处理基础Python 中提供了对时间日期的多种多样的处理方式,主要是在 time …...

C语言学习及复习笔记-【5】C 运算符
文章目录5. C 运算符5.1 关系运算符5.2 逻辑运算符5.3 位运算符5.4 杂项运算符 ↦ sizeof & 三元5.5 例子1). 利用异或 ^ 来交换两个数的值,而且不引入其他变量。2). 利用位与 & 运算,判断一个整数是否是2的整数次幂。3). 不同长度的数据进行位运…...
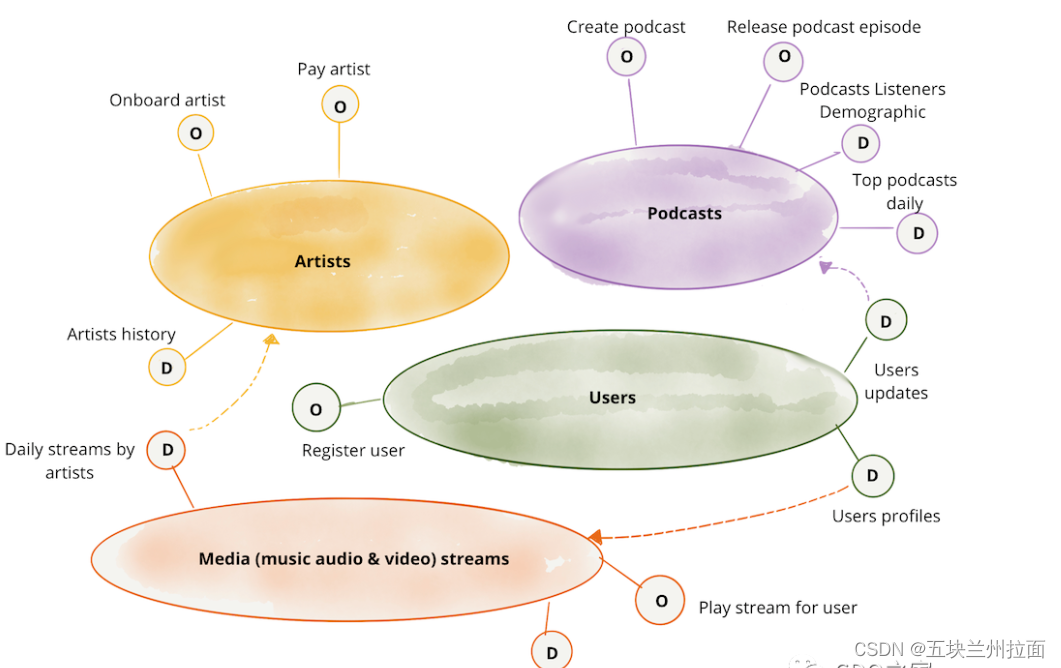
数仓、数据湖、湖仓一体、数据网格
第一代:数据仓库 定义 为解决数据库面对数据分析的不足,孕育出新一类产品数据仓库。数据仓库(Data Warehouse)是一个面向主题的、集成的、相对稳定的、反映历史变化的数据集合,用于支持管理决策和信息的全局共享。 数…...

C语言【atoi函数】
C语言【atoi函数】🫅系统atoi函数🫅 模拟实现atoi函数看到atoi函数,有人又会问有这个函数,我怎么没用过。那就说明:不是你刷题太少,就是atoi函数存在感太低。 这篇函数就带你领略atoi函数的魅力 Ǻ…...

一起学习用Verilog在FPGA上实现CNN----(八)integrationFC设计
1 integrationFC设计 LeNet-5网络结构全连接部分如图所示,该部分有2个全连接层,1个TanH激活层,1个SoftMax激活层: 图片来自附带的技术文档《Hardware Documentation》 integrationFC部分原理图,如图所示,…...

面试题总结
1.js的数据类型 分为基本数据类型和引用数据类型。 基本数据类型 ES5的5种:Null,undefined,Boolean,Number,String, ES6新增:Symbol表示独一无二的值 ES10新增:BigInt 表示任意大的…...
go进阶(1) -深入理解goroutine并发运行机制
并发指的是同时进行多个任务的程序,Web处理请求,读写处理操作,I/O操作都可以充分利用并发增长处理速度,随着网络的普及,并发操作逐渐不可或缺 一、goroutine简述 在Golang中一个goroutines就是一个执行单元ÿ…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
