摆动输入连杆夹持机构
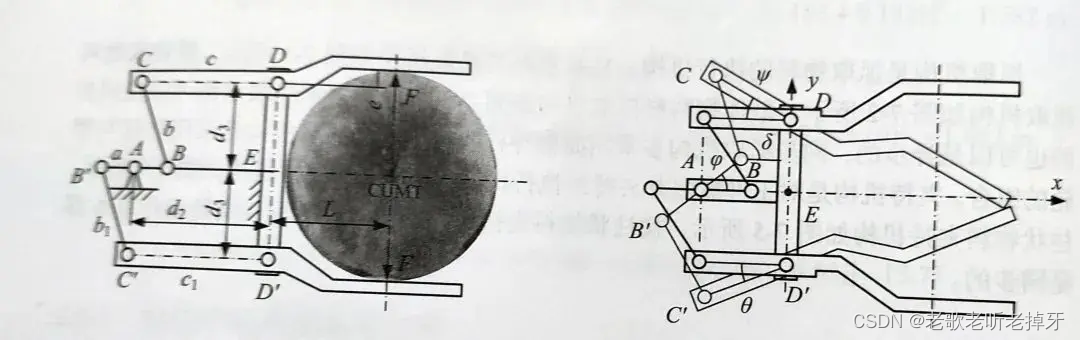
1、运动与受力分析
import sympy as sy
import numpy as np
import matplotlib.pyplot as plt
a,a1,b,b1,c,c1,d2,d3,fi,F,L,e= sy.symbols('a,a1,b,b1,c,c1,d2,d3,fi,F,L,e')
'''
A(-d2,0)
D(0,d3)
B(-d2+a*cos(fi),a*sin(fi))
C(-c*cos(pu),d3+c*sin(pu))
B'=(-d2+a*cos(fi+pi),a*sin(fi+pi))
C'=(c1*cos(theta+pi),-d3+c1*sin(theta+pi))'''
A1=2*c*(d3-a*sy.sin(fi))
B1=-2*c*(d2-a*sy.cos(fi))
C1=(d2-a*sy.cos(fi))**2+(d3-a*sy.sin(fi))**2+c**2-b**2
pu=2*sy.atan((-A1+sy.sqrt(A1**2+B1**2-C1**2))/(C1-B1))
delta=sy.atan((d3+c*sy.sin(pu)-a*sy.sin(fi))/(-c*sy.cos(pu)+d2-a*sy.cos(fi)))+sy.pi
A2=2*c1*(d3-a*sy.sin(fi))
B2=-2*c1*(d2+a*sy.cos(fi))
C2=(d2+a*sy.cos(fi))**2+(d3-a*sy.sin(fi))**2+c1**2-b1**2
theta=2*sy.atan((-A2+sy.sqrt(A2**2+B2**2-C2**2))/(C2-B2))
beta=sy.atan((d3-c1*sy.sin(theta)+a*sy.sin(fi))/(-c1*sy.cos(theta)+d2+a*sy.cos(fi)))
F23=F*(L*sy.cos(pu)+e*sy.sin(pu))/(c*sy.sin(delta+pu))
F23I=-F*(L*sy.cos(theta)+e*sy.sin(theta))/(c1*sy.sin(beta-theta))
M=F23*a*sy.sin(delta-fi)-F23I*a*(beta-fi)
pu_c=pu.subs({a:30,b:79.5,b1:79.5,c:120,c1:120,d2:120,d3:74,e:15,L:100})
delta_c=delta.subs({a:30,b:79.5,b1:79.5,c:120,c1:120,d2:120,d3:74,e:15,L:100})
fi_v=10*np.pi/180
xa=-120
ya=0
xb=-120+30*np.cos(fi_v)
yb=30*np.sin(fi_v)
Cx=-c*sy.cos(pu)
Cy=d3+c*sy.sin(pu)
xc=Cx.subs({a:30,b:79.5,b1:79.5,c:120,c1:120,d2:120,d3:74,e:15,L:100,fi:fi_v})
yc=Cy.subs({a:30,b:79.5,b1:79.5,c:120,c1:120,d2:120,d3:74,e:15,L:100,fi:fi_v})
xd=0
yd=74
B1x=-d2+a*sy.cos(fi+sy.pi)
B1y=a*sy.sin(fi+sy.pi)
C1x=c1*sy.cos(theta+sy.pi)
C1y=-d3+c1*sy.sin(theta+sy.pi)
xb1=B1x.subs({a:30,b:79.5,b1:79.5,c:120,c1:120,d2:120,d3:74,e:15,L:100,fi:fi_v})
yb1=B1y.subs({a:30,b:79.5,b1:79.5,c:120,c1:120,d2:120,d3:74,e:15,L:100,fi:fi_v})
xc1=C1x.subs({a:30,b:79.5,b1:79.5,c:120,c1:120,d2:120,d3:74,e:15,L:100,fi:fi_v})
yc1=C1y.subs({a:30,b:79.5,b1:79.5,c:120,c1:120,d2:120,d3:74,e:15,L:100,fi:fi_v})
# sy.plot(pu_c,(fi,0,80*sy.pi/180))
# sy.plot(delta_c,(fi,0,80*sy.pi/180))fig = plt.figure(figsize=(5, 4))
plt.rcParams['xtick.direction'] = 'in' # 将x周的刻度线方向设置向内
plt.rcParams['ytick.direction'] = 'in' # 将y轴的刻度方向设置向内
plt.rcParams['axes.unicode_minus']=False
# plt.rcParams['font.family'] = ["Times New Roman"] # 字体设置为Times NewRoman
plt.rcParams['font.sans-serif'] = ['SimHei']
clist = ['blue', 'red', 'green', 'black', 'darkgreen', 'lime', 'gold', 'purple', 'green', 'cyan', 'salmon', 'grey','mediumvioletred', 'darkkhaki', 'gray', 'darkcyan', 'violet', 'powderblue']
markerlst = ['o', '*', 'x', '>', '<', '^', 'D', 'd', '1', '2', '3', '4', 'o', '*', 'x', '>', '<', '^', 'D', 'd','1', '2', '3', '4', 'o', '*', 'x', '>', '<', '^', 'D', 'd', '1', '2', '3', '4']
linestylelst = ['-', '--', '-.', ':', '-', '--', '-.', ':', '-', '--', '-.', ':', '-', '--', '-.', ':', '-', '--','-.', ':', '-', '--', '-.', ':']
# 圆的基本信息
# 1.圆半径
r = 30
# 2.圆心坐标
a, b = (-120, 0.)
# ==========================================
# 参数方程画圆形
theta = np.arange(0, 2 * np.pi, 0.01)
x = a + r * np.cos(theta)
y = b + r * np.sin(theta)
plt.plot(x, y, c=clist[0])
plt.plot([xa,xb],[ya,yb],c=clist[1])
plt.plot([xb,xc],[yb,yc],c=clist[2])
plt.plot([xc,xd],[yc,yd],c=clist[3])
plt.plot([xd,xd],[-yd,yd],c=clist[4])
plt.plot([xa,xb1],[ya,yb1],c=clist[5])
plt.plot([xb1,xc1],[yb1,yc1],c=clist[6])
plt.plot([xc1,xd],[yc1,-yd],c=clist[7])
plt.show()
2、机构动画
import sympy as sy
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
a,a1,b,b1,c,c1,d2,d3,fi,F,L,e= sy.symbols('a,a1,b,b1,c,c1,d2,d3,fi,F,L,e')
'''
A(-d2,0)
D(0,d3)
B(-d2+a*cos(fi),a*sin(fi))
C(-c*cos(pu),d3+c*sin(pu))
B'=(-d2+a*cos(fi+pi),a*sin(fi+pi))
C'=(c1*cos(theta+pi),-d3+c1*sin(theta+pi))'''
A1=2*c*(d3-a*sy.sin(fi))
B1=-2*c*(d2-a*sy.cos(fi))
C1=(d2-a*sy.cos(fi))**2+(d3-a*sy.sin(fi))**2+c**2-b**2
pu=2*sy.atan((-A1+sy.sqrt(A1**2+B1**2-C1**2))/(C1-B1))
delta=sy.atan((d3+c*sy.sin(pu)-a*sy.sin(fi))/(-c*sy.cos(pu)+d2-a*sy.cos(fi)))+sy.pi
A2=2*c1*(d3-a*sy.sin(fi))
B2=-2*c1*(d2+a*sy.cos(fi))
C2=(d2+a*sy.cos(fi))**2+(d3-a*sy.sin(fi))**2+c1**2-b1**2
theta=2*sy.atan((-A2+sy.sqrt(A2**2+B2**2-C2**2))/(C2-B2))
beta=sy.atan((d3-c1*sy.sin(theta)+a*sy.sin(fi))/(-c1*sy.cos(theta)+d2+a*sy.cos(fi)))
F23=F*(L*sy.cos(pu)+e*sy.sin(pu))/(c*sy.sin(delta+pu))
F23I=-F*(L*sy.cos(theta)+e*sy.sin(theta))/(c1*sy.sin(beta-theta))
M=F23*a*sy.sin(delta-fi)-F23I*a*(beta-fi)
pu_c=pu.subs({a:30,b:79.5,b1:79.5,c:120,c1:120,d2:120,d3:74,e:15,L:100})
delta_c=delta.subs({a:30,b:79.5,b1:79.5,c:120,c1:120,d2:120,d3:74,e:15,L:100})
Cx = -c * sy.cos(pu)
Cy = d3 + c * sy.sin(pu)
B1x = -d2 + a * sy.cos(fi + sy.pi)
B1y = a * sy.sin(fi + sy.pi)
C1x = c1 * sy.cos(theta + sy.pi)
C1y = -d3 + c1 * sy.sin(theta + sy.pi)
cx = sy.lambdify(fi, Cx.subs({a: 30, b: 79.5, b1: 79.5, c: 120, c1: 120, d2: 120, d3: 74, e: 15, L: 100}), modules='numpy')
cy = sy.lambdify(fi, Cy.subs({a: 30, b: 79.5, b1: 79.5, c: 120, c1: 120, d2: 120, d3: 74, e: 15, L: 100}), modules='numpy')
b1x = sy.lambdify(fi, B1x.subs({a: 30, b: 79.5, b1: 79.5, c: 120, c1: 120, d2: 120, d3: 74, e: 15, L: 100}), modules='numpy')
b1y = sy.lambdify(fi, B1y.subs({a: 30, b: 79.5, b1: 79.5, c: 120, c1: 120, d2: 120, d3: 74, e: 15, L: 100}), modules='numpy')
c1x = sy.lambdify(fi, C1x.subs({a: 30, b: 79.5, b1: 79.5, c: 120, c1: 120, d2: 120, d3: 74, e: 15, L: 100}), modules='numpy')
c1y = sy.lambdify(fi, C1y.subs({a: 30, b: 79.5, b1: 79.5, c: 120, c1: 120, d2: 120, d3: 74, e: 15, L: 100}), modules='numpy')
# sy.plot(pu_c,(fi,0,80*sy.pi/180))
# sy.plot(delta_c,(fi,0,80*sy.pi/180))fig = plt.figure(figsize=(5, 4))
plt.rcParams['xtick.direction'] = 'in' # 将x周的刻度线方向设置向内
plt.rcParams['ytick.direction'] = 'in' # 将y轴的刻度方向设置向内
plt.rcParams['axes.unicode_minus']=False
# plt.rcParams['font.family'] = ["Times New Roman"] # 字体设置为Times NewRoman
plt.rcParams['font.sans-serif'] = ['SimHei']
clist = ['blue', 'red', 'green', 'black', 'darkgreen', 'lime', 'gold', 'purple', 'green', 'cyan', 'salmon', 'grey','mediumvioletred', 'darkkhaki', 'gray', 'darkcyan', 'violet', 'powderblue']
markerlst = ['o', '*', 'x', '>', '<', '^', 'D', 'd', '1', '2', '3', '4', 'o', '*', 'x', '>', '<', '^', 'D', 'd','1', '2', '3', '4', 'o', '*', 'x', '>', '<', '^', 'D', 'd', '1', '2', '3', '4']
linestylelst = ['-', '--', '-.', ':', '-', '--', '-.', ':', '-', '--', '-.', ':', '-', '--', '-.', ':', '-', '--','-.', ':', '-', '--', '-.', ':']# 创建绘图框架
fig, ax = plt.subplots()# 定义每帧图像的处理函数
'''
定义了一个处理函数draw_frame(),该函数根据当前的“帧数”(即第几张图)生成对应的x和y的坐标点
'''
def draw_frame(i):fi_v = i * np.pi / 180xa = -120ya = 0xb = -120 + 30 * np.cos(fi_v)yb = 30 * np.sin(fi_v)xc = cx(fi_v)yc = cy(fi_v)xd = 0yd = 74xb1 = b1x(fi_v)yb1 = b1y(fi_v)xc1 = c1x(fi_v)yc1 = c1y(fi_v)# 绘制图形ax.clear()r = 30# 2.圆心坐标x0, y0 = (-120, 0.)# ==========================================# 参数方程画圆形theta = np.arange(0, 2 * np.pi, 0.01)x = x0 + r * np.cos(theta)y = y0 + r * np.sin(theta)ax.plot(x, y, c=clist[0])ax.plot([xa, xb], [ya, yb], c=clist[1])ax.plot([xb, xc], [yb, yc], c=clist[2])ax.plot([xc, xd], [yc, yd], c=clist[3])ax.plot([xd, xd], [-yd, yd], c=clist[4])ax.plot([xa, xb1], [ya, yb1], c=clist[5])ax.plot([xb1, xc1], [yb1, yc1], c=clist[6])ax.plot([xc1, xd], [yc1, -yd], c=clist[7])ax.axis("equal")# 固定X轴、Y轴的范围ax.set_ylim(ymin=-150, ymax=150)ax.set_xlim(xmin=-160, xmax=10)plt.tight_layout()# 生成动画对象
'''
FuncAnimation()函数生成了一个动画对象anim,该对象会在循环中调用draw_frame()函数,并以50毫秒的时间间隔循环展示100帧图像
'''
anim = FuncAnimation(fig, draw_frame, frames=80, interval=50)
# 使用pillow将动画保存为GIF图片
anim.save('finger.gif', writer='pillow')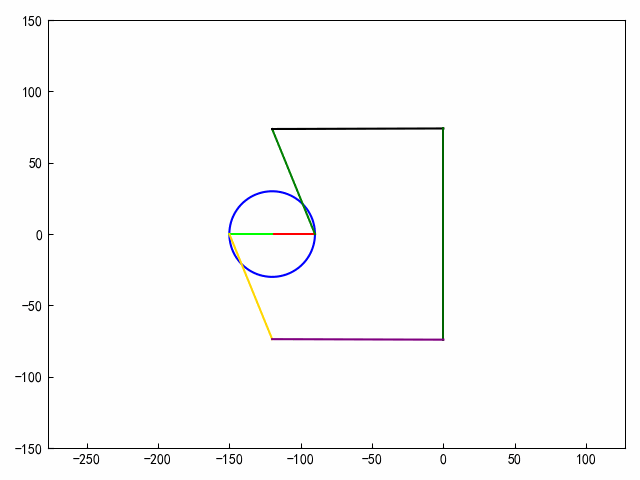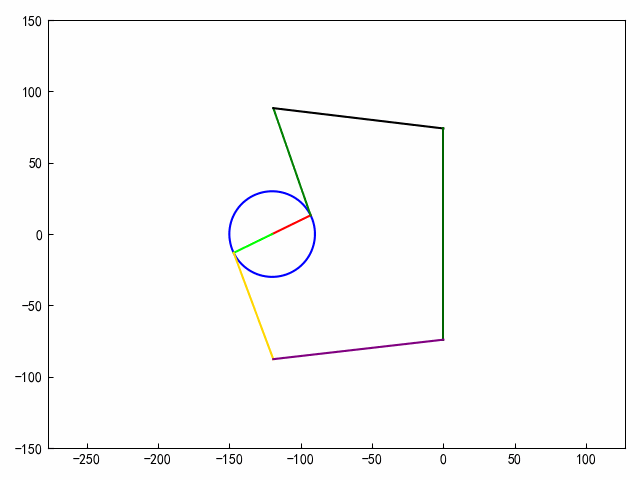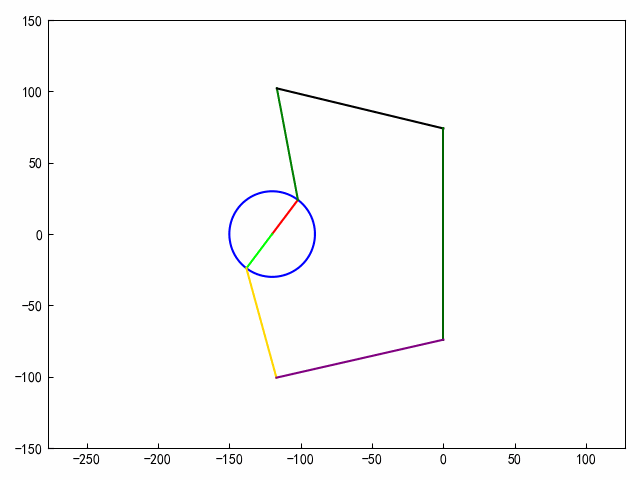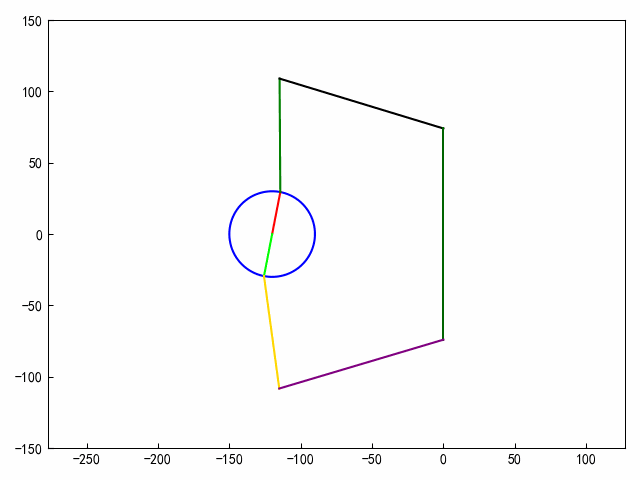
相关文章:

摆动输入连杆夹持机构
1、运动与受力分析 import sympy as sy import numpy as np import matplotlib.pyplot as plt a,a1,b,b1,c,c1,d2,d3,fi,F,L,e sy.symbols(a,a1,b,b1,c,c1,d2,d3,fi,F,L,e)A(-d2,0) D(0,d3) B(-d2a*cos(fi),a*sin(fi)) C(-c*cos(pu),d3c*sin(pu)) B(-d2a*cos(fipi),a*sin(fipi…...

C++——类与对象(下篇)
前言 前面已经介绍了类与对象(上),类与对象(中)的两篇文章,下面是类与对象的最后一些重要知识点的介绍和总结。 目录 再谈构造函数Static成员友元内部类匿名对象拷贝对象时的一些编译器优化再次理解封装…...

stm32 freeRTOS lwip TCP快速发送,内存泄露问题
现象1: 发送缓慢,tcp_write之后要等200多ms才能过发送出去,而且粘包严重。 解决办法 tcp_write之后,立马调用tcp_output ,tcp就会立马发送。 tcp_write tcp_output 现象2: 持续快速发送和接受TCP数据出…...

Ei、Scopus双检索 | 2024年第三届人工智能与机器学习前沿国际会议(FAIML 2024)
会议简介 Brief Introduction 2024年第三届人工智能与机器学习前沿国际会议(FAIML 2024) 会议时间:2024年4月26日-28日 召开地点:中国宜昌 大会官网:www.faiml.org FAIML 2024将围绕“人工智能与机器学习”的最新研究领域而展开,为…...

win10环境下搭建QT+opencv
安装步骤 源码编译安装免编译/cmake安装vs2022环境安装 问题解决 modules/core/CMakeFiles/opencv_core.dir/vs_version.rc.obj] Error 1 PS D:\Qt\Tools\mingw730_64\bin> D:\Qt\Tools\mingw730_64\bin\windres.exe D:\Opencv\opencv\opencv\build\modules\core\vs_ver…...
React16、18 使用 Redux
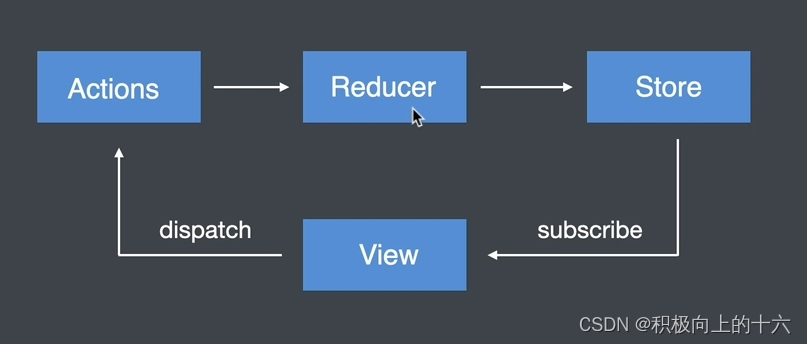
Redux 核心 Redux 介绍 Redux 是javaScript 状态容器,提供可预测化的状态管理 Redux 工作流程 Actions:对象,描述对状态进行怎样的操作 Reducer:函数,操作状态并返回新的状态 Store:存储状态的容器&am…...

【Python】Python运算符/部分函数对应的双下划线魔法方法
先说下Python版本:【Python 3.7.8】 以下用图片表格展示,一是防扒,二是没精力改成md格式。 还有就是内容肯定没有完全包含(而且也很难做到),像是__reduce__与py自带模块pickle有关(pickle用于对象序列化/反序列化)、sys.getsizeo…...
Macs Fan Control 1.5.16 Pro for mac风扇调节软件
Macs Fan Control是一款专门为 Mac 用户设计的软件,它可以帮助用户控制和监控 Mac 设备的风扇速度和温度。这款软件允许用户手动调整风扇速度,以提高设备的散热效果,减少过热造成的风险。 Macs Fan Control 可以在菜单栏上显示当前系统温度和…...

某技术公司技术二面面试题总结
存在一个单体架构的服务,怎么拆分为微服务的架构 将一个单体应用程序拆分成微服务架构是一个复杂的过程,需要深入的计划和实施。以下是一般的步骤和策略,可以帮助您成功地将单体应用程序拆分为微服务: 理解单体应用程序ÿ…...

初试小程序轮播组件
文章目录 一、轮播组件(一)swiper组件1、功能描述2、属性说明 (二)swiper-item组件1、功能描述2、属性说明 二、案例演示(一)运行效果(二)实现步骤1、创建小程序项目2、准备图片素材…...

Centos7 Yum安装PHP7.2
1、安装源 安装php72w,是需要配置额外的yum源地址的,否则会报错不能找到相关软件包。 php高版本的yum源地址,有两部分,其中一部分是epel-release,另外一部分来自webtatic。如果跳过epel-release的话,安装…...

2020年09月 C/C++(三级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C编程(1~8级)全部真题・点这里 第1题:铺砖 对于一个2行N列的走道。现在用12,22的砖去铺满。问有多少种不同的方式。 时间限制:3000 内存限制:131072 输入 整个测试有多组数据,请做到文件底结束。每行给出…...
30天入门Python(基础篇)——第2天:Python安装(保姆级)与IDE的认识与选择+详细安装教程
文章目录 专栏导读上一节课回顾1、Python解释器的安装查看各个版本的Python解释器①、ok,双击安装②、这里我们选择【自定义】安装, 下面的【将Python添加在环境变量】大家一定要打个勾③、点击【Next】进行下一步④、这里不建议安装在C盘, 点击【Browse】我在F盘创…...

软件测试/测试开发丨ChatGPT:带你进入智能对话的新时代
简介 人工智能时代来临 我们正处于AI的iPhone时刻。——黄仁勋(英伟达CEO) ChatGPT 好得有点可怕了,我们距离危险的强人工智能不远了。——马斯克(Tesla/SpaceX/Twitter CEO) 以上的内容说明我们现在正处于一个技术大…...
logback/log4j基本配置和标签详解
什么是logback logback 继承自 log4j,它建立在有十年工业经验的日志系统之上。它比其它所有的日志系统更快并且更小,包含了许多独特并且有用的特性。 logback.xml 首先直接上配置,我在项目过程中发现一些同时遇到需要logback文件的时候就去…...

雅思 《九分达人》阅读练习(二)
目录 雅思阅读练习 《九分达人》test3 paragraph3 1.单词含义要记准确,敏感度要上来。 2.找准定位,之后理解句子大致含义。 说说关于判断题的做题方法 关于“承认”有哪些单词 同替词汇 think 可以用什么其他单词来替换 单词 一些疑问 I have…...
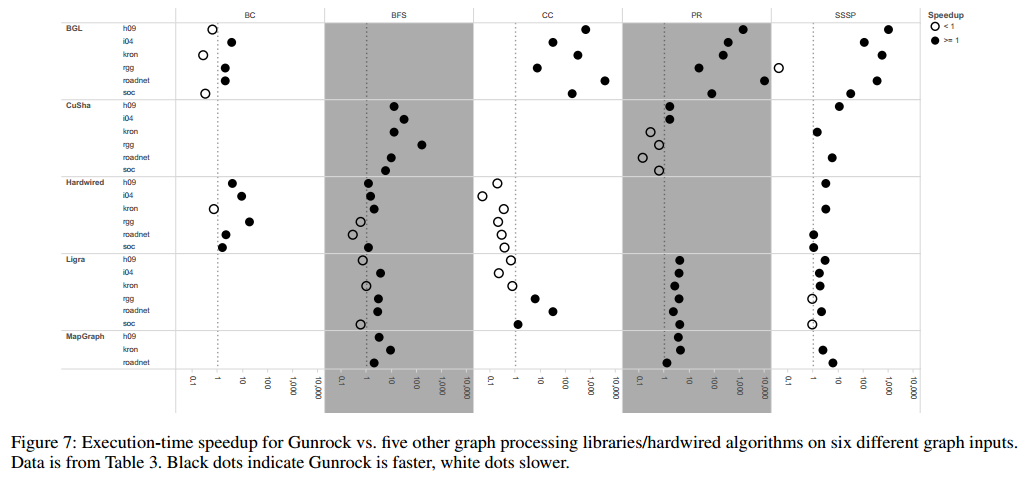
[论文笔记] Gunrock: A High-Performance Graph Processing Library on the GPU
Gunrock: A High-Performance Graph Processing Library on the GPU Gunrock: GPU 上的高性能图处理库 [Paper] [Code] PPoPP’16 摘要 Gunrock, 针对 GPU 的高层次批量同步图处理系统. 采用了一种新方法抽象 GPU 图分析: 实现了以数据为中心(data-centric)的抽象, 以在结点…...

A Guide to PriorityQueue
原文链接:https://blog.csdn.net/ohwang/article/details/116934308 PriorityQueue 又叫 优先队列 注意1: PriorityQueue是用数组实现,数组大小可以动态增加,容量无限。 优先队列采用的是堆排序(默认为最小堆ÿ…...

Jenkins教程—构建多分支流水线项目
本教程向你展示如何使用Jenkins协调一个用 Node Package Manager (npm) 管理的简单 Node.js 和 React 项目, 并同时 为开发和产品环境交付不同的结果。 在开始本教程之前,建议你前往 教程概览 页面,并至少完成一个 介绍教程, 从而…...
)
【vxe-table】@enter.keyup.native实现在列表中回车光标向右移动聚焦及vxe-table的一些方法的使用(具体实现+踩坑篇)
需求: vxe-table表格 1、新增的时候,vxe-table第一行的第一个输入框聚焦 2、输入完成后,按回车,自动跳到同一行的下一个输入框 3、当在同一行的最后一个输入框输入完成后,按回车跳回第一个输入框并选中状态且复选框为选…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
