算法训练营day44|动态规划 part06:完全背包 (完全背包、 LeetCode518. 零钱兑换 II、377. 组合总和 Ⅳ )
文章目录
- 完全背包
- 518. 零钱兑换 II (求组合方法数)
- 思路分析
- 代码实现
- 思考总结
- 377. 组合总和 Ⅳ (求排列方法数)
- 思路分析
- 代码实现
- 思考总结
完全背包
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
依然举这个例子:
背包最大重量为4。
物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
每件商品都有无限个!
问背包能背的物品最大价值是多少?
01背包和完全背包唯一不同就是体现在遍历顺序上,
01背包的核心代码:
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
01背包内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。
**而完全背包的物品是可以添加多次的,所以要从小到大去遍历,**即:
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
dp状态图如下:

01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了,一维dp数组的两个for循环先后循序一定是先遍历物品,再遍历背包容量。
在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序是无所谓的!
因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。
完整代码:
// 先遍历物品,在遍历背包
void test_CompletePack() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagWeight = 4;vector<int> dp(bagWeight + 1, 0);for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}cout << dp[bagWeight] << endl;
}
int main() {test_CompletePack();
}
// 先遍历背包,再遍历物品
void test_CompletePack() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagWeight = 4;vector<int> dp(bagWeight + 1, 0);for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量for(int i = 0; i < weight.size(); i++) { // 遍历物品if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}cout << dp[bagWeight] << endl;
}
int main() {test_CompletePack();
}518. 零钱兑换 II (求组合方法数)
题目链接🔥🔥
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
示例 1:
输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2:
输入: amount = 3, coins = [2]
输出: 0
解释: 只用面额2的硬币不能凑成总金额3。
示例 3:
输入: amount = 10, coins = [10]
输出: 1
注意,你可以假设:
0 <= amount (总金额) <= 5000
1 <= coin (硬币面额) <= 5000
硬币种类不超过 500 种
结果符合 32 位符号整数
思路分析
本题和纯完全背包不一样,纯完全背包是凑成背包最大价值是多少,而本题是要求凑成总金额的物品组合个数!
注意题目描述中是凑成总金额的硬币组合数,为什么强调是组合数呢?
例如示例一:
5 = 2 + 2 + 1
5 = 2 + 1 + 2
这是一种组合,都是 2 2 1。
如果问的是排列数,那么上面就是两种排列了。
组合不强调元素之间的顺序,排列强调元素之间的顺序。
- 确定dp数组以及下标的含义
dp[j]:凑成总金额j的货币组合数为dp[j]
- 确定递推公式
dp[j] 就是所有的dp[j - coins[i]](考虑coins[i]的情况)相加。
所以递推公式:dp[j] += dp[j - coins[i]];
这个递推公式在这篇494. 目标和中就讲解了,求装满背包有几种方法,公式都是:dp[j] += dp[j - nums[i]];
- dp数组如何初始化
首先dp[0]一定要为1,dp[0] = 1是 递归公式的基础。如果dp[0] = 0 的话,后面所有推导出来的值都是0了。
那么 dp[0] = 1 有没有含义,其实既可以说凑成总金额0的货币组合数为1,也可以说 凑成总金额0的货币组合数为0,好像都没有毛病。
但题目描述中,也没明确说 amount = 0 的情况,结果应该是多少。
这里我认为题目描述还是要说明一下,因为后台测试数据是默认,amount = 0 的情况,组合数为1的。
下标非0的dp[j]初始化为0,这样累计加dp[j - coins[i]]的时候才不会影响真正的dp[j]
dp[0]=1还说明了一种情况:如果正好选了coins[i]后,也就是j-coins[i] == 0的情况表示这个硬币刚好能选,此时dp[0]为1表示只选coins[i]存在这样的一种选法。
- 确定遍历顺序
本题中我们是外层for循环遍历物品(钱币),内层for遍历背包(金钱总额),还是外层for遍历背包(金钱总额),内层for循环遍历物品(钱币)呢?
完全背包的两个for循环的先后顺序都是可以的。但本题就不行了!
因为纯完全背包求得装满背包的最大价值是多少,和凑成总和的元素有没有顺序没关系,即:有顺序也行,没有顺序也行!
而本题要求凑成总和的组合数,元素之间明确要求没有顺序。两个for循环的先后顺序可就有说法了。
我们先来看 外层for循环遍历物品(钱币),内层for遍历背包(金钱总额)的情况。
代码如下:
for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量dp[j] += dp[j - coins[i]];}
}
假设:coins[0] = 1,coins[1] = 5。
那么就是先把1加入计算,然后再把5加入计算,得到的方法数量只有{1, 5}这种情况。而不会出现{5, 1}的情况。
所以这种遍历顺序中dp[j]里计算的是组合数!
如果把两个for交换顺序,代码如下:
for (int j = 0; j <= amount; j++) { // 遍历背包容量for (int i = 0; i < coins.size(); i++) { // 遍历物品if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];}
}
背包容量的每一个值,都是经过 1 和 5 的计算,包含了{1, 5} 和 {5, 1}两种情况。
此时dp[j]里算出来的就是排列数!
- 举例推导dp数组
输入: amount = 5, coins = [1, 2, 5] ,dp状态图如下:

代码实现
class Solution {
public:int change(int amount, vector<int>& coins) {vector<int> dp(amount+1,0);dp[0]=1;for(int i=0;i<coins.size();i++){for(int j=coins[i];j<=amount;j++){dp[j]+=dp[j-coins[i]];}}return dp[amount];}
};
思考总结
难点在于遍历顺序!
在求装满背包有几种方案的时候,认清遍历顺序是非常关键的。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
和下一道题好好对比。
377. 组合总和 Ⅳ (求排列方法数)
题目链接🔥🔥
给定一个由正整数组成且不存在重复数字的数组,找出和为给定目标正整数的组合的个数。
示例:
nums = [1, 2, 3]
target = 4
所有可能的组合为: (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1)
请注意,顺序不同的序列被视作不同的组合。
因此输出为 7。
思路分析
元素相同顺序不同的组合算两个组合,其实就是求排列!
其本质是本题求的是排列总和,而且仅仅是求排列总和的个数,并不是把所有的排列都列出来。
如果本题要把排列都列出来的话,只能使用回溯算法爆搜。
动规五部曲分析如下:
- 确定dp数组以及下标的含义
dp[i]: 凑成目标正整数为i的排列个数为dp[i]
- 确定递推公式
在494. 目标和和518.零钱兑换II中我们已经讲过了,求装满背包有几种方法,递推公式一般都是dp[j] += dp[j - nums[i]];
本题也一样。
- dp数组如何初始化
因为递推公式dp[i] += dp[i - nums[j]]的缘故,dp[0]要初始化为1,这样递归其他dp[i]的时候才会有数值基础。
至于dp[0] = 1 有没有意义呢?
其实没有意义,所以我也不去强行解释它的意义了,因为题目中也说了:给定目标值是正整数! 所以dp[0] = 1是没有意义的,仅仅是为了推导递推公式。
至于非0下标的dp[i]应该初始为多少呢?
初始化为0,这样才不会影响dp[i]累加所有的dp[i - nums[j]]。
- 确定遍历顺序
本题要求的是排列,那么这个for循环嵌套的顺序可以有说法了。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
如果把遍历nums(物品)放在外循环,遍历target的作为内循环的话,举一个例子:计算dp[4]的时候,结果集只有 {1,3} 这样的集合,不会有{3,1}这样的集合,因为nums遍历放在外层,3只能出现在1后面!
所以本题遍历顺序最终遍历顺序:target(背包)放在外循环,将nums(物品)放在内循环,内循环从前到后遍历。
- 举例来推导dp数组
我们再来用示例中的例子推导一下:

代码实现
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<int> dp(target+1,0);dp[0]=1;for(int j=0;j<=target;j++){for(int i=0;i<nums.size();i++){//C++测试用例有两个数相加超过int的数据,所以需要在if里加上dp[j] < INT_MAX - dp[j - nums[i]]。if(j>=nums[i]&&dp[j] < INT_MAX - dp[j - nums[i]]) dp[j]+=dp[j-nums[i]]; }}return dp[target];}
};
思考总结
求装满背包有几种方法,递归公式都是一样的,没有什么差别,但关键在于遍历顺序!
相关文章:

算法训练营day44|动态规划 part06:完全背包 (完全背包、 LeetCode518. 零钱兑换 II、377. 组合总和 Ⅳ )
文章目录 完全背包518. 零钱兑换 II (求组合方法数)思路分析代码实现思考总结 377. 组合总和 Ⅳ (求排列方法数)思路分析代码实现思考总结 完全背包 完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。 依然举这个例子: 背包最大重量为4。 物…...

包管理工具--》其他包管理器之cnpm、pnpm、nvm
包管理工具系列文章目录 一、包管理工具--》npm的配置及使用(一) 二、包管理工具--》npm的配置及使用(二) 三、包管理工具--》发布一个自己的npm包 四、包管理工具--》yarn的配置及使用 五、包管理工具--》其他包管理器之cnpm…...

线性代数的学习和整理22:矩阵的点乘(草稿)
4 矩阵乘法 A,B两个同阶同秩N阵,看上去结构一样,但两厢相乘,在做在右,地位差别巨大。 在左,你就是基,是空间的根本,是坐标系,是往哪去、能到哪的定海神针,是如来佛手&a…...
如何在Windows中使用C#填写和提取PDF表单
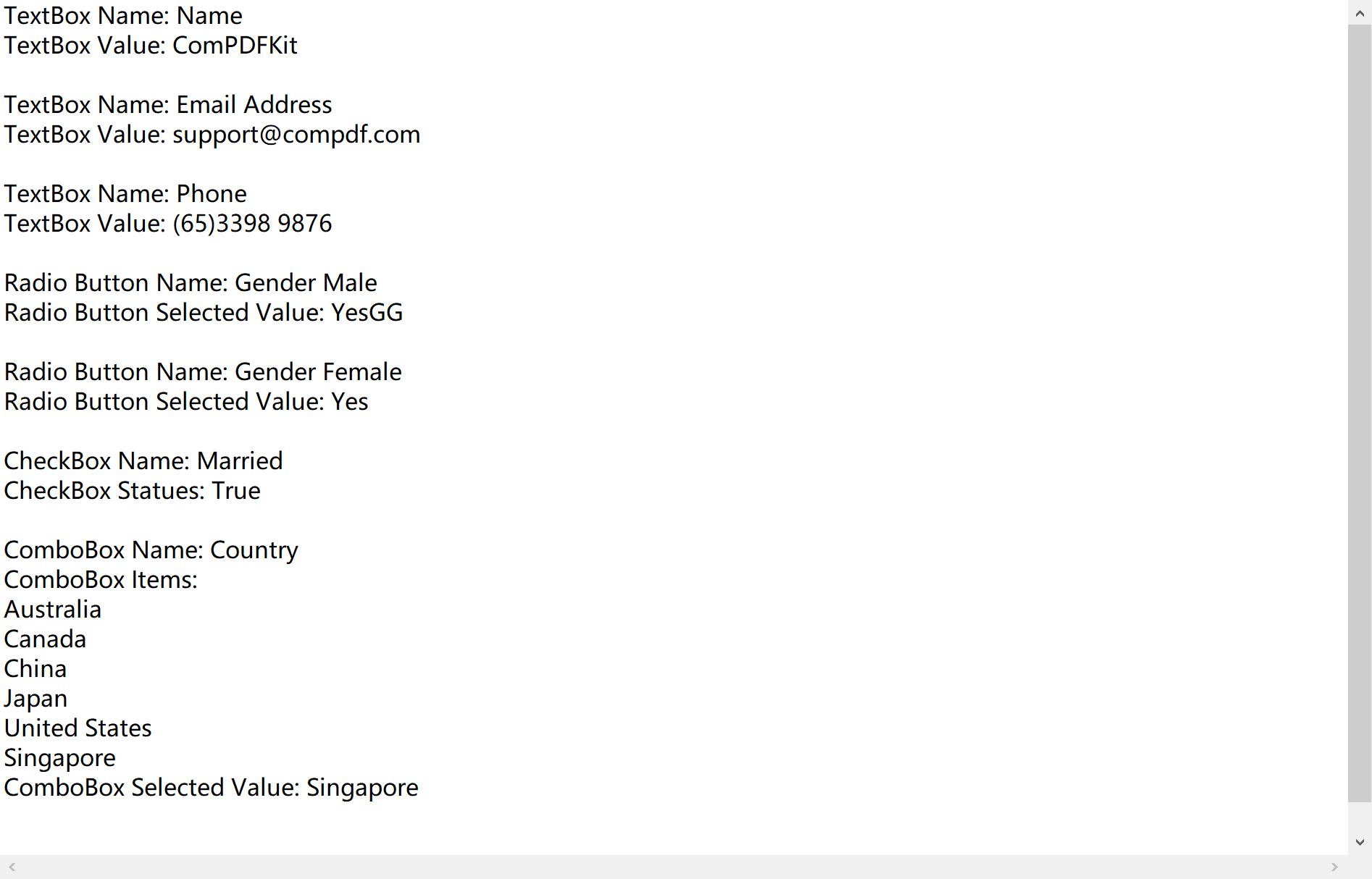
如何在Windows中使用C#填写和提取PDF表单 PDF表单不仅允许用户填写和提交数据,也允许用户创建各种表单域收集用户的数据,并通过提取表单字段值,将收集和合并提交的数据进一步分析或处理。PDF通过电子方式填写、保存和共享的形式,…...

microsoft.office.interop.word 怎样 读取 某个汉字 字体颜色为红色
SKY[管理]筱傑 SKY[机器]筱淋 microsoft.office.interop.word 怎样 读取 某个汉字 字体颜色为红色呢? 要读取某个汉字的字体颜色是否为红色,您可以使用Microsoft.Office.Interop.Word来进行操作。以下是一个示例代码,可以帮助您实现该功能&am…...

第二十二章 Classes - 调用类方法的快捷方式
文章目录 第二十二章 Classes - 调用类方法的快捷方式调用类方法的快捷方式类参数 第二十二章 Classes - 调用类方法的快捷方式 调用类方法的快捷方式 使用 ObjectScript 调用类方法时,在以下情况下可以省略包(或更高级别的包):…...

标准C++day2——函数重载、默认形参和引用
一、函数重载 1、什么是函数重载? 在同一作用域下,函数名相同,参数列表不同的函数构成重载关系 函数重载与返回值类型、参数名无关 与作用域是否相同,以及参数列表的数量、参数类型、常属性不同等有关 2、C是如何实现函数重载的&a…...

Qt5下遍历QList的方法
lines定义如下 QMap<QString,Line> lines; Line的定义如下 class Line{protected:QString name;QColor color;QList<int> total_stations; // all statuibQList<QString> start_stas,end_stas; //start end stationQList<QList<QString>>sta_li…...

Leetcode 剑指 Offer II 043. 完全二叉树插入器
题目难度: 中等 原题链接 今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复 剑指offer2 就能看到该系列当前连载的所有文章了, 记得关注哦~ 题目描述 完全二叉树是每一层(除最后一层外)都是完…...
链路追踪Skywalking应用实战
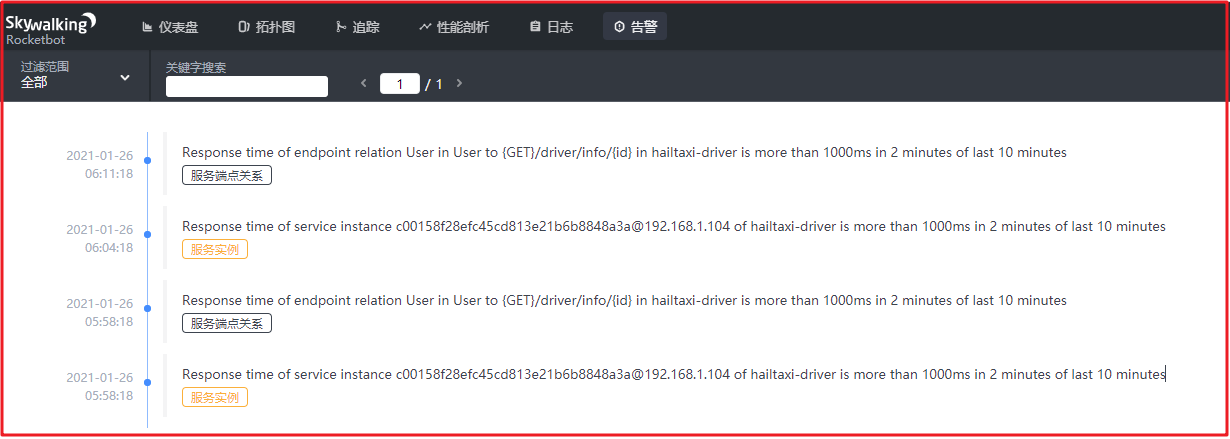
目录 1 Skywalking应用2 agent下载3 agent应用3.1 应用名配置3.2 IDEA集成使用agent3.3 生产环境使用agent 4 Rocketbot4.1 Rocketbot-仪表盘4.2 Rocketbot-拓扑图4.3 追踪4.4 性能分析4.5 告警4.5.1 警告规则详解4.5.2 Webhook规则4.5.3 自定义Webhook消息接收 1 Skywalking应…...

提升你的Android开发技能:从AR/VR沉浸到UI设计和故障排除
文章目录 探索最新AR/VR应用在教育、游戏、医疗等领域的应用教育领域游戏领域医疗领域 深入了解Android内存管理与性能优化的方法与技巧垃圾回收机制内存泄漏使用弱引用避免过度渲染内存优化图像优化延迟加载Android中的调试技术应用程序分析 分享如何提高Android应用的易用性和…...
Arm 架构 Ubuntu 使用 Docker 安装 Gitlab 并使用
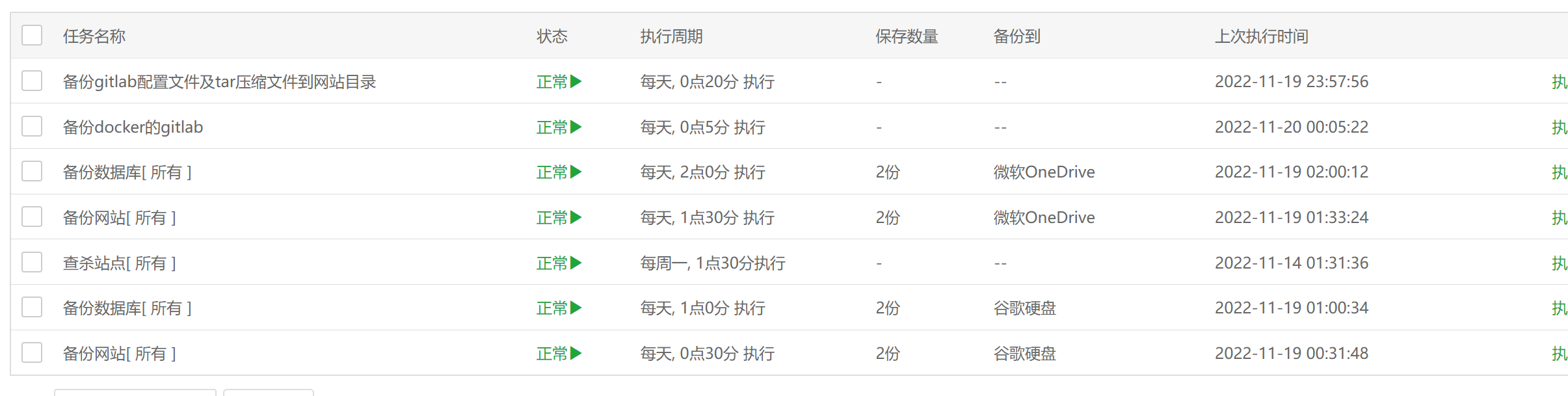
官方 gitlab 文档 我的系统是 arm 架构的 ubuntu 官网没有提供 arm 架构的 docker 的 gitlab 的安装方式,直接安装的也是后来加的,文档也是随笔带过,,,我用到了,记录一下 默认已经安装了 docker 在 docker …...
百度地图3D棱柱鼠标事件
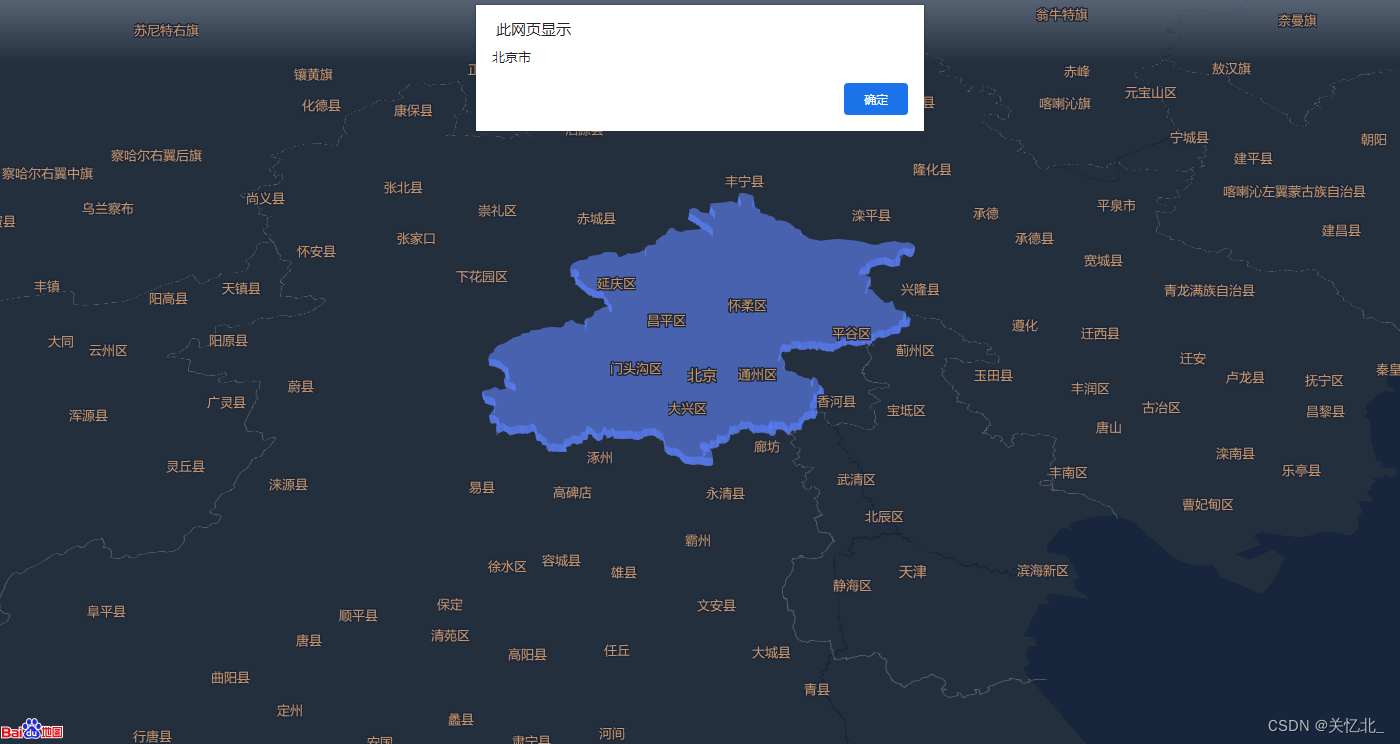
百度地图2D API JavaScript API | 百度地图API SDK 百度地图3D API jspopularGL | 百度地图API SDK 3D棱柱效果如下 一. 渲染地图 var map new BMapGL.Map(container, {style: {styleJson: styleJson2} }) map.centerAndZoom(new BMapGL.Point(116.404, 39.925), 9); map…...

PHP调用java class 类实现文件签名
PHP调用java class 类实现文件签名 原始代码改造开始PHP内调用方式起因:对接某平台API接口,发送的文件需要做 SM3 签名,对方平台是java写的,只有java加密示例,照着java的加密算法翻译为PHP版本,在编码转换上始终有些差异。没办法,只能想办法使用他们的java方式。 原始代…...

信号和槽机制
信号和槽机制 信号和槽的使用自定义信号槽信号槽机制是Qt框架中引以为豪机制之一,所谓信号槽实际就是类似于Gof中的观察者模式。当某个事件发生以后,比如点击一下按钮,按钮就会触发一个信号,这个信号按照类似广播的形式进行发送,如果某个对象对这个信号感兴趣就会触发连接…...
计算机视觉领域经典模型汇总(2023.09.08
一、RCNN系列 1、RCNN RCNN是用于目标检测的经典方法,其核心思想是将目标检测任务分解为两个主要步骤:候选区域生成和目标分类。 候选区域生成:RCNN的第一步是生成可能包含目标的候选区域,RCNN使用传统的计算机视觉技术&#x…...
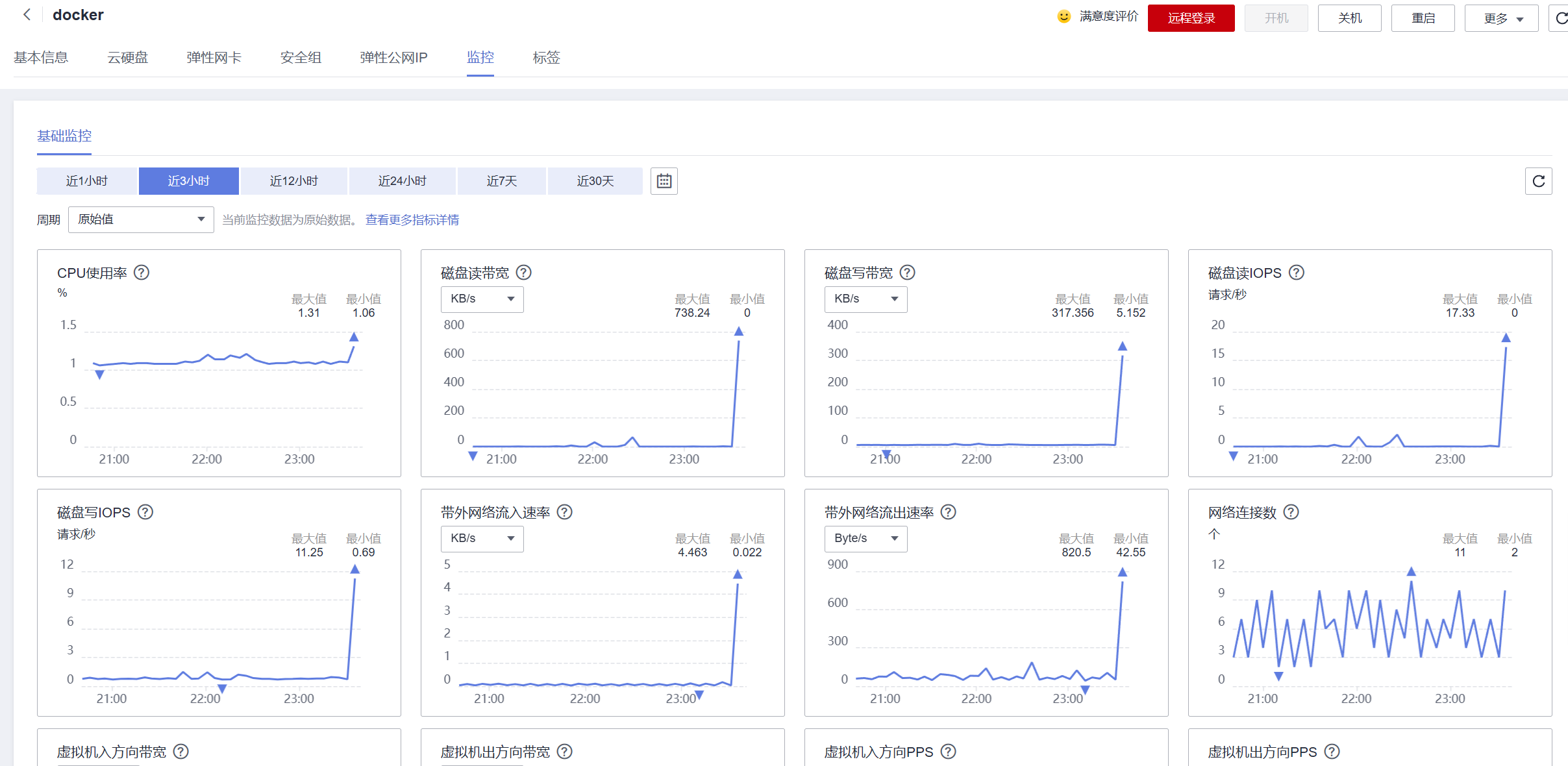
华为云云耀云服务器L实例评测|在 Centos Docker 中使用Nginx部署Vue项目
目录 前言 项目构建 使用CentOS部署 安装Nginx 配置Nginx 项目启动 访问重定向 使用Docker部署 编写docker文件 dockerfile nginx dockercompose 项目启动 前言 本期我们测试在云耀云服务器L实例中分别演示如何在 系统镜像Centos 与 应用镜像 Docker 中使用Nginx…...

高频知识汇总 |【计算机网络】面试题汇总(万字长文通俗易懂)
我之前也已经在写了好几篇高频知识点汇总,简要介绍一下,有需要的同学可以点进去先收藏,之后用到时可以看一看。如果有帮助的话,希望大家给个赞,给个收藏!有疑问的也可以在评论区留言讨论,能帮的…...

6.Flask-APScheduler定时任务框架
1.下载安装 pip install flask-apscheduler2.基本使用 from flask import Flask from flask_apscheduler import APScheduler app Flask(__name__) aps APScheduler() # 配置定时任务 scheduler { id: job1, func: scheduler:task, # 指向一个Python函数或方法…...

电脑入门:路由器访问控制列表基础知识
路由器访问控制列表基础知识 1、什么是访问控制列表? 访问控制列表在Cisco IOS软件中是一个可选机制,可以配置成过滤器来控制数据包,以决定该数据包是继续向前传递到它的目的地还是丢弃。 …...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...
