Leetcode 剑指 Offer II 043. 完全二叉树插入器
题目难度: 中等
原题链接
今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复
剑指offer2就能看到该系列当前连载的所有文章了, 记得关注哦~
题目描述
完全二叉树是每一层(除最后一层外)都是完全填充(即,节点数达到最大,第 n 层有 2n-1 个节点)的,并且所有的节点都尽可能地集中在左侧。
设计一个用完全二叉树初始化的数据结构 CBTInserter,它支持以下几种操作:
- CBTInserter(TreeNode root) 使用根节点为 root 的给定树初始化该数据结构;
- CBTInserter.insert(int v) 向树中插入一个新节点,节点类型为 TreeNode,值为 v 。使树保持完全二叉树的状态,并返回插入的新节点的父节点的值;
- CBTInserter.get_root() 将返回树的根节点。
示例 1:
- 输入:inputs =
["CBTInserter","insert","get_root"], inputs =[[[1]],[2],[]] - 输出:
[null,1,[1,2]]
示例 2:
- 输入:inputs =
["CBTInserter","insert","insert","get_root"], inputs =[[[1,2,3,4,5,6]],[7],[8],[]] - 输出:
[null,3,4,[1,2,3,4,5,6,7,8]]
提示:
- 最初给定的树是完全二叉树,且包含 1 到 1000 个节点。
- 每个测试用例最多调用 CBTInserter.insert 操作 10000 次。
- 给定节点或插入节点的每个值都在 0 到 5000 之间。
题目思考
- 如何利用完全二叉树的性质?
解决方案
思路
- 分析题目, 为了保证插入新节点后仍保持完全二叉树的状态, 我们需要知道当前待插入的节点位置
- 根据完全二叉树的性质, 这里有两种可能:
- 当前最底层还有空位, 则插入位置就是上个插入节点的相邻右侧
- 当前最底层没有空位了, 则需要往下新开辟一层, 并插入该层最左侧
- 那如何判断当前最底层还有没有空位呢?
- 我们可以利用按层 BFS, 记录最初给定的树的每一层节点信息, 这样就可以得到树高度, 以及最底层的节点个数
- 然后根据完全二叉树的性质, 如果某层高度是 h(从 0 开始), 那么当其节点个数达到 2^h 就表示这一层满了, 否则就还有空位
- 最后再按照上面的判断, 就可以知道当前待插入节点位置了
- 接下来我们需要得到待插入节点的父节点, 这里同样可以利用完全二叉树的性质: 某一层第 i 个节点的父节点一定是上一层第 i/2 个节点 (i 下标从 0 开始)
- 举两个例子:
- 某一层第 0 个节点的左子节点是下一层第 0 个节点, 右子节点是下一层第 1 个节点
- 某一层第 2 个节点的左子节点是下一层第 4 个节点, 右子节点是下一层第 5 个节点
- 得到父节点之后, 我们判断其左子节点是否为空, 是的话就说明待插入节点是其左子节点, 否则就是其右子节点
- 下面的代码就对应了上面的整个过程, 并且有详细的注释, 方便大家理解
复杂度
- 时间复杂度 O(1): 每次 insert 只需要几个常数时间的操作
- 空间复杂度 O(N): 需要存储所有节点到对应的层
代码
class CBTInserter:def __init__(self, root: TreeNode):self.root = rootself.levels = []q = [root]while q:curlen = len(q)for node in q[:curlen]:if node.left:q.append(node.left)if node.right:q.append(node.right)# 将当前层加入levels列表self.levels.append(q[:curlen])q = q[curlen:]def insert(self, v: int) -> int:h = len(self.levels) - 1if len(self.levels[-1]) == 1 << h:# 最底层满了, 需要新建一层self.levels.append([])# 父节点下标是当前待插入下标除以2pi = len(self.levels[-1]) // 2# 父节点在倒数第二层, 根据其下标得到父节点parent = self.levels[-2][pi]# 追加父子连接node = TreeNode(v)if not parent.left:# 父节点的左子节点还不存在, 将其指定为nodeparent.left = nodeelse:# 父节点的左子节点已存在, 将右子节点指定为nodeparent.right = node# 将node添加到最底层self.levels[-1].append(node)return parent.valdef get_root(self) -> TreeNode:return self.root
大家可以在下面这些地方找到我~😊
我的 GitHub
我的 Leetcode
我的 CSDN
我的知乎专栏
我的头条号
我的牛客网博客
我的公众号: 算法精选, 欢迎大家扫码关注~😊

相关文章:

Leetcode 剑指 Offer II 043. 完全二叉树插入器
题目难度: 中等 原题链接 今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复 剑指offer2 就能看到该系列当前连载的所有文章了, 记得关注哦~ 题目描述 完全二叉树是每一层(除最后一层外)都是完…...
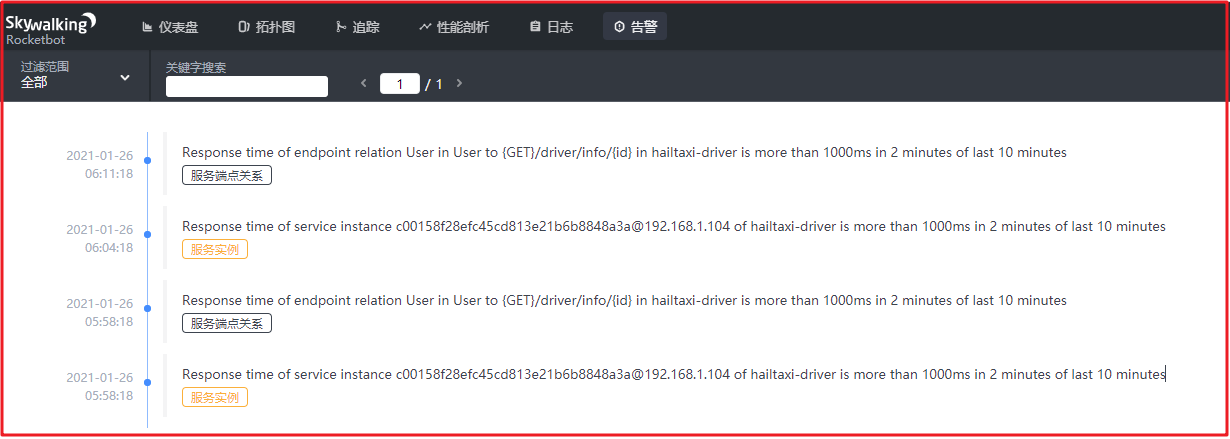
链路追踪Skywalking应用实战
目录 1 Skywalking应用2 agent下载3 agent应用3.1 应用名配置3.2 IDEA集成使用agent3.3 生产环境使用agent 4 Rocketbot4.1 Rocketbot-仪表盘4.2 Rocketbot-拓扑图4.3 追踪4.4 性能分析4.5 告警4.5.1 警告规则详解4.5.2 Webhook规则4.5.3 自定义Webhook消息接收 1 Skywalking应…...

提升你的Android开发技能:从AR/VR沉浸到UI设计和故障排除
文章目录 探索最新AR/VR应用在教育、游戏、医疗等领域的应用教育领域游戏领域医疗领域 深入了解Android内存管理与性能优化的方法与技巧垃圾回收机制内存泄漏使用弱引用避免过度渲染内存优化图像优化延迟加载Android中的调试技术应用程序分析 分享如何提高Android应用的易用性和…...
Arm 架构 Ubuntu 使用 Docker 安装 Gitlab 并使用
官方 gitlab 文档 我的系统是 arm 架构的 ubuntu 官网没有提供 arm 架构的 docker 的 gitlab 的安装方式,直接安装的也是后来加的,文档也是随笔带过,,,我用到了,记录一下 默认已经安装了 docker 在 docker …...
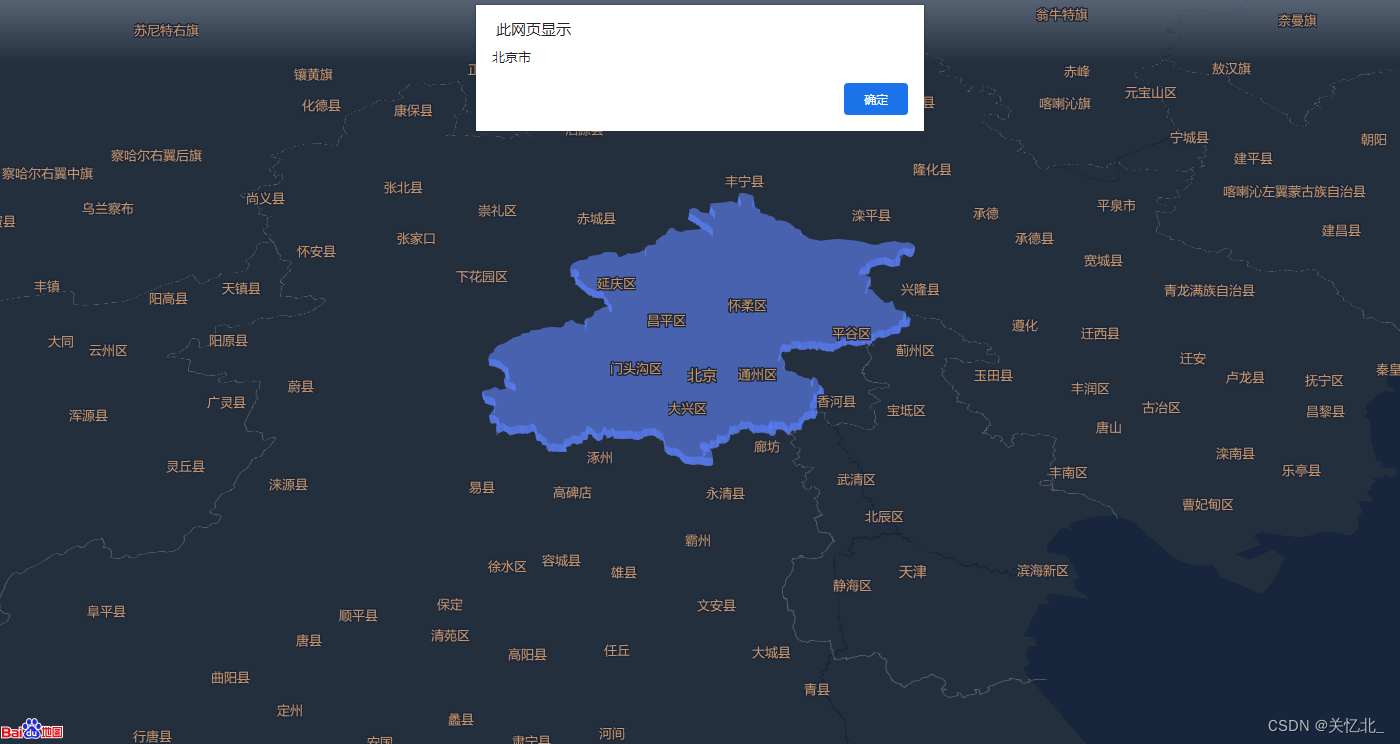
百度地图3D棱柱鼠标事件
百度地图2D API JavaScript API | 百度地图API SDK 百度地图3D API jspopularGL | 百度地图API SDK 3D棱柱效果如下 一. 渲染地图 var map new BMapGL.Map(container, {style: {styleJson: styleJson2} }) map.centerAndZoom(new BMapGL.Point(116.404, 39.925), 9); map…...

PHP调用java class 类实现文件签名
PHP调用java class 类实现文件签名 原始代码改造开始PHP内调用方式起因:对接某平台API接口,发送的文件需要做 SM3 签名,对方平台是java写的,只有java加密示例,照着java的加密算法翻译为PHP版本,在编码转换上始终有些差异。没办法,只能想办法使用他们的java方式。 原始代…...

信号和槽机制
信号和槽机制 信号和槽的使用自定义信号槽信号槽机制是Qt框架中引以为豪机制之一,所谓信号槽实际就是类似于Gof中的观察者模式。当某个事件发生以后,比如点击一下按钮,按钮就会触发一个信号,这个信号按照类似广播的形式进行发送,如果某个对象对这个信号感兴趣就会触发连接…...
计算机视觉领域经典模型汇总(2023.09.08
一、RCNN系列 1、RCNN RCNN是用于目标检测的经典方法,其核心思想是将目标检测任务分解为两个主要步骤:候选区域生成和目标分类。 候选区域生成:RCNN的第一步是生成可能包含目标的候选区域,RCNN使用传统的计算机视觉技术&#x…...
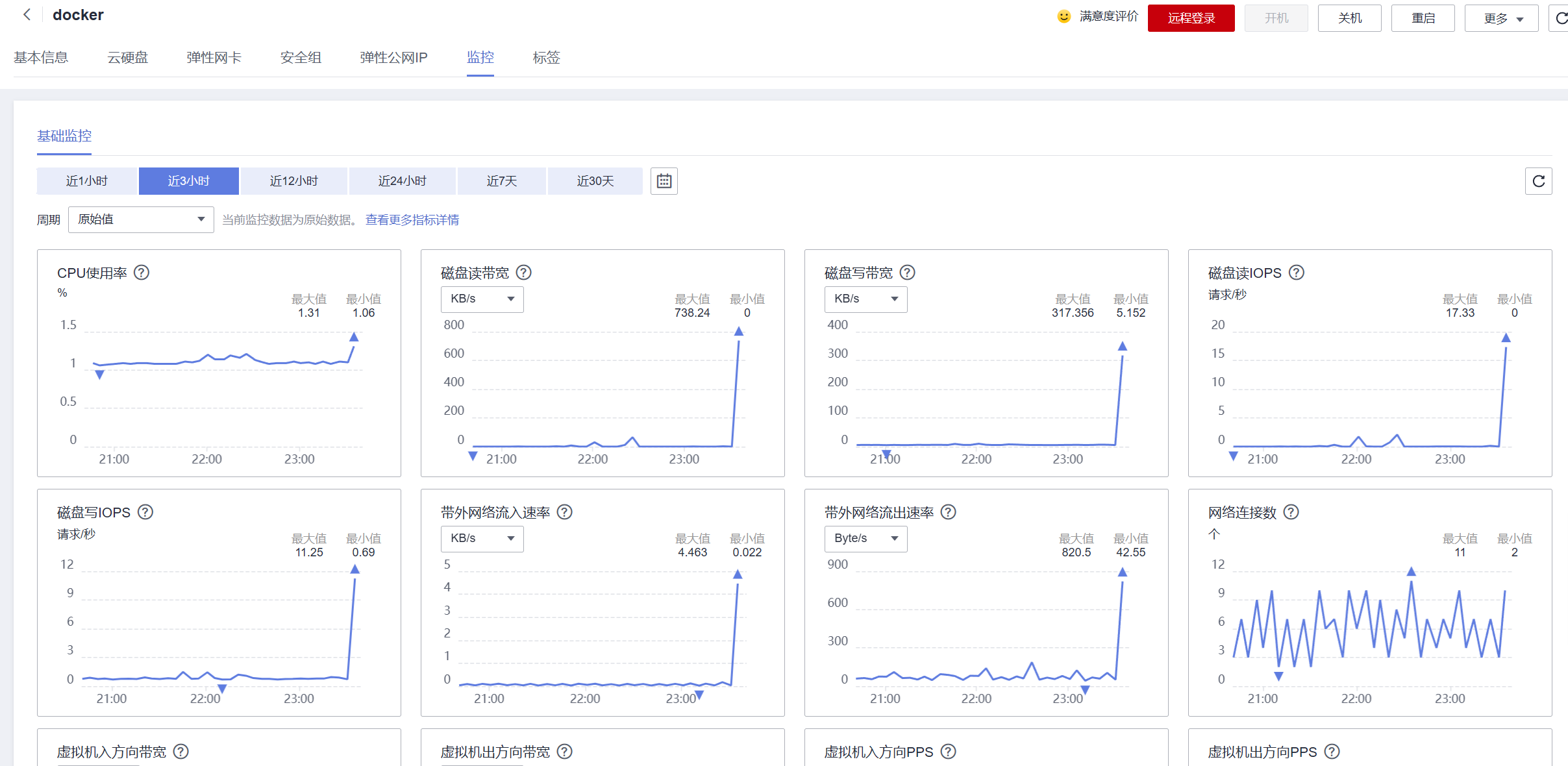
华为云云耀云服务器L实例评测|在 Centos Docker 中使用Nginx部署Vue项目
目录 前言 项目构建 使用CentOS部署 安装Nginx 配置Nginx 项目启动 访问重定向 使用Docker部署 编写docker文件 dockerfile nginx dockercompose 项目启动 前言 本期我们测试在云耀云服务器L实例中分别演示如何在 系统镜像Centos 与 应用镜像 Docker 中使用Nginx…...

高频知识汇总 |【计算机网络】面试题汇总(万字长文通俗易懂)
我之前也已经在写了好几篇高频知识点汇总,简要介绍一下,有需要的同学可以点进去先收藏,之后用到时可以看一看。如果有帮助的话,希望大家给个赞,给个收藏!有疑问的也可以在评论区留言讨论,能帮的…...

6.Flask-APScheduler定时任务框架
1.下载安装 pip install flask-apscheduler2.基本使用 from flask import Flask from flask_apscheduler import APScheduler app Flask(__name__) aps APScheduler() # 配置定时任务 scheduler { id: job1, func: scheduler:task, # 指向一个Python函数或方法…...

电脑入门:路由器访问控制列表基础知识
路由器访问控制列表基础知识 1、什么是访问控制列表? 访问控制列表在Cisco IOS软件中是一个可选机制,可以配置成过滤器来控制数据包,以决定该数据包是继续向前传递到它的目的地还是丢弃。 …...

目标检测笔记(十四): 使用YOLOv8完成对图像的目标检测任务(从数据准备到训练测试部署的完整流程)
文章目录 一、目标检测介绍二、YOLOv8介绍三、源码获取四、环境搭建4.1 环境检测 五、数据集准备六、 模型训练6.1 方式一6.2 方式二6.3 针对其他任务 七、模型验证八、模型测试九、模型转换9.1 转onnx9.1.1 方式一 9.2 转tensorRT9.2.1 trtexec9.2.2 代码转换9.2.3 推理代码 一…...
windows系统edge浏览器退出账户后还能免密登录的解决方式
edge浏览器明明退出登录了,还能不用输密码一键点击就能登录; 这是因为微软的煞笔产品经理用脚后跟想出来的方案。 解决方案: 去设置里的账号管理,注销自己的微软账号登录;如果你发现自己并没有登录,那么看…...
在Spring Boot项目中使用JPA
1.集成Spring Data JPA Spring Boot提供了启动器spring-boot-starter-data-jpa,只需要添加启动器(Starters)就能实现在项目中使用JPA。下面一步一步演示集成Spring Data JPA所需的配置。 步骤01 添加JPA依赖。 首先创建新的Spring Boot项目…...

探讨Socks5代理IP在跨境电商与网络游戏中的网络安全应用
随着全球互联网的迅猛发展,跨境电商和在线游戏成为了跨国公司和游戏开发商的新战场。然而,与此同时,网络安全问题也日益突出。本文将探讨如何利用Socks5代理IP来增强跨境电商和网络游戏的网络安全,保障数据传输的隐私和安全性。 …...

T检验的前提条件|独立性|方差齐性|随机抽样
T检验是一种用于比较两组数据均值是否存在显著差异的统计方法,但在进行T检验之前,有一些前提条件需要满足,以确保结果的准确性和可靠性。这些前提条件包括: 正态性:T检验要求数据在每个组内都服从正态分布。正态性可以…...
【GO语言基础】变量常量
系列文章目录 【Go语言学习】ide安装与配置 【GO语言基础】前言 【GO语言基础】变量常量 【GO语言基础】数据类型 【GO语言基础】运算符 文章目录 系列文章目录常量和枚举变量声明全局变量声明大小写敏感 总结 常量和枚举 使用const关键字声明常量,并为每个常量提…...

C++QT day3
1> 自行封装一个栈的类,包含私有成员属性:栈的数组、记录栈顶的变量 成员函数完成:构造函数、析构函数、拷贝构造函数、入栈、出栈、清空栈、判空、判满、获取栈顶元素、求栈的大小 2> 自行封装一个循环顺序队列的类,包含…...
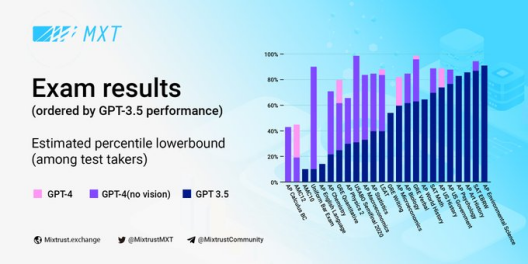
AI时代的较量,MixTrust能否略胜一筹?
人工智能的能力正在迅速接近人类,而在许多细分领域,已经超越了人类。虽然短期内这个突破是否会导致人工通用智能(AGI)还不清楚,但我们现在有的模型被训练成在数字交互中完美地模仿高能人类。尽管AGI仍不确定࿰…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
