day-41 代码随想录算法训练营(19)动态规划 part 03
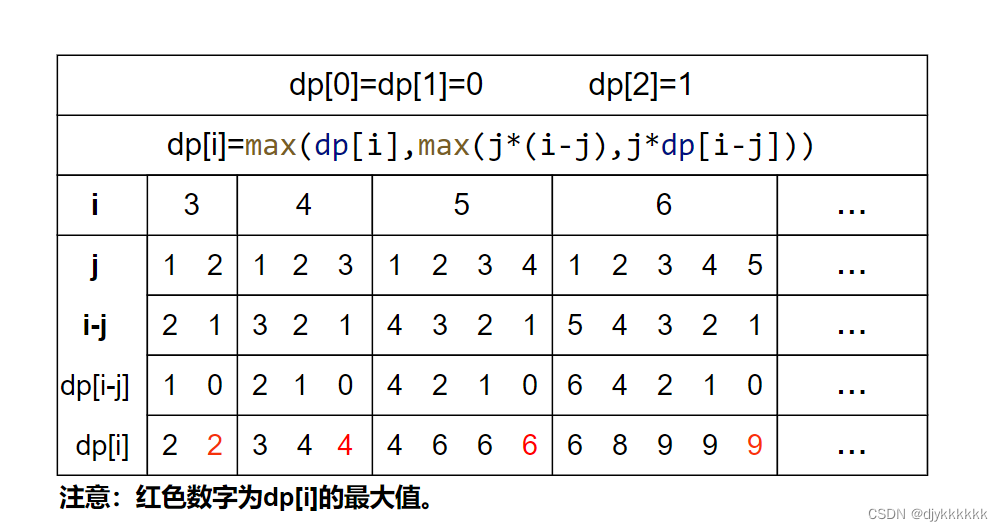
343.整数拆分
思路:
- 1.dp存储的是第i个数,拆分之后最大乘积
- 2.dp[i]=max(dp[i],max(j*(i-j),j*dp[i-j]));
- 3.初始化:dp[0]=dp[1]=0,dp[2]=1;
- 4.遍历顺序:外层循环 3-n,内层循环 1-i
2.涉及两次取max:
- dp[i] 表示拆开的最大乘积,因为涉及多次计算
- j*(i-j) 表示拆成两个数
- j*dp[i-j] 表示拆成两个以上的数(dp[i-j] 就是剩下没拆的数,拆开的最大乘积)
class Solution {
public:int integerBreak(int n) {vector<int>dp(n+1,0);dp[2]=1;for(int i=3;i<=n;i++){for(int j=1;j<i;j++){dp[i]=max(dp[i],max(j*(i-j),j*dp[i-j]));cout<<i<<" "<<dp[i]<<endl;}}return dp[n];}
};
96.不同的二叉搜索树
分析:1-n有几种二叉搜索树
-
1.以1-n每个数为根节点
-
2.判断根节点左边和右边各有几个节点,只有结点数相同,组合的二叉搜索树种数就是一样的。
思路:
- 1.dp存储n个节点有多少种二叉搜索树
- 2.dp[i]=dp[i-1]*dp[n-i];
- 3.初始化:dp[0]=dp[1]=1,dp[2]=2;
- 4.遍历顺序:3-n
416.分割等和子集
分析:
- 数组要求分成两个等和子集,所以一定要有子集和为总和的一半
- 转换为:在集合中找数字,看能否组合成总和的一半值的子集
- 转换为:在总和一半容量的背包里,寻找子集刚好装满
思路一:
1.dp存储:容量为 j 时,装入物品的最大值
2.dp [ j ] =max ( dp [ j ] ,dp [ j - nums [i] ] + nums [ i ] )
3.初始化:所有值初始化为0
4.遍历顺序:外层遍历数字(顺序,物品),内层遍历数字(倒序,背包容量)
class Solution {
public:bool canPartition(vector<int>& nums) {int total=0;for(auto it:nums) total+=it;//求出总和if(total%2!=0) return false;//过滤不可拆成两半的情况int target=total/2;//背包容量vector<int>dp(10001,0);for(int i=0;i<nums.size();i++){//遍历物品for(int j=target;j>=nums[i];j--){//背包容量递减,最少能装入一个物品dp[j]=max(dp[j],dp[j-nums[i]]+nums[i]);//dp[j] 是不装当前物品//dp[j-nums[i]]+nums[i] 是装当前物品}}if(dp[target]==target) return true;//背包容量为target,装了target重的物品return false;}
};相关文章:

day-41 代码随想录算法训练营(19)动态规划 part 03
343.整数拆分 思路: 1.dp存储的是第i个数,拆分之后最大乘积2.dp[i]max(dp[i],max(j*(i-j),j*dp[i-j]));3.初始化:dp[0]dp[1]0,dp[2]1;4.遍历顺序:外层循环 3-n,内层循环 1-i 2.涉及两次取max: dp[i] 表…...
)
K8S安装部署 初始化操作(一)
准备好服务器和服务器资源 ip hostnameip资源 (2核2G也可以)k8s-master 192.168.37.1184核 4G 40G硬盘k8s-node1192.168.37.1192核 2G 20G硬盘k8s-node2192.168.37.1202核 2G 20G硬盘 初始操作三台同时执行 1、关闭防火墙 [rootlocalhost ~]# s…...
【多线程案例】单例模式(懒汉模式和饿汉模式)
文章目录 1. 什么是单例模式?2. 立即加载/“饿汉模式”3. 延时加载/“懒汉模式”3.1 第一版3.2 第二版3.3 第三版3.4 第四版 1. 什么是单例模式? 提起单例模式,就必须介绍设计模式,而设计模式就是在软件设计中,针对特殊…...
Anaconda - 操作系统安装程序 简要介绍
Anaconda 简要介绍 1. Anaconda 简介2. Anaconda 体系结构3. Anaconda 开发模型4. Anaconda 启动概述5. Anaconda 源码1. 接口2. 自定义组件3. 硬盘分区:使用python-blivet包4. Bootloader5. 各个步骤的配置:6. 安装软件包:7. 安装控制&#…...

【数据库设计】向量搜索HNSW算法优化
做向量存储的过程中,遇到向量搜索的情况处理,HNSW算法是目前向量搜索的主要算法之一,采用的是图算法,主要的问题是使用内存大,训练时间长。做算法优化过程中获得部分技巧,分享出来。 一、算法本身的优化 对…...

多通道振弦数据记录仪应用桥梁安全监测的关键要点
多通道振弦数据记录仪应用桥梁安全监测的关键要点 随着近年来桥梁建设和维护的不断推进,桥梁安全监测越来越成为公共关注的焦点。多通道振弦数据记录仪因其高效、准确的数据采集和处理能力,已经成为桥梁安全监测中不可或缺的设备。本文将从以下几个方面…...

深入了解HTTP代理的工作原理
HTTP代理是一种常见的网络代理方式,它可以帮助用户隐藏自己的IP地址,保护个人隐私和安全。了解HTTP代理的工作原理对于使用HTTP代理的用户来说非常重要。本文将深入介绍HTTP代理的工作原理。 代理服务器的作用 HTTP代理的工作原理基于代理服务器的作用。…...

2023年高教社杯数学建模国赛选题人数+C题进阶版修改思路详解
C题思路 修改版 C题保奖 数据预处理 3σ原则 区间判断法、人为判定 问题 1 聚类分析进行简单的分类 相互关系 数据服从正态分布(K-S检验等判定分布类型后) 才能做person相关性 图表结合(热力图、数据结果表) 分布规律 宏…...
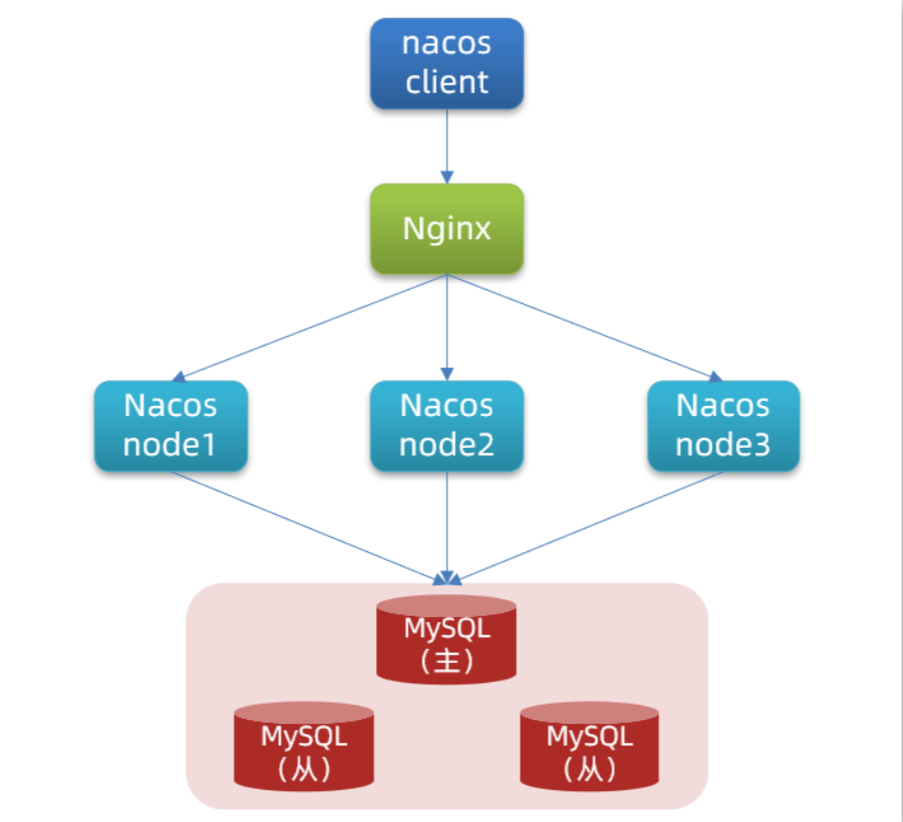
第三章微服务配置中心
文章目录 Nacos配置中心统一配置管理在nacos中添加配置文件从微服务拉取配置 配置热更新多环境共享配置 搭建Nacos集群搭建集群初始化数据库配置Nacos启动nginx反向代理 Nacos配置中心 Nacos配置管理 Nacos除了可以做注册中心,同样可以做配置管理来使用。 统一配置…...

箭头函数(arrow function)与普通函数之间的区别是什么?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 语法简洁性:⭐ this 的绑定:⭐ 不能用作构造函数:⭐ 没有 arguments 对象:⭐ 不适用于方法:⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上…...
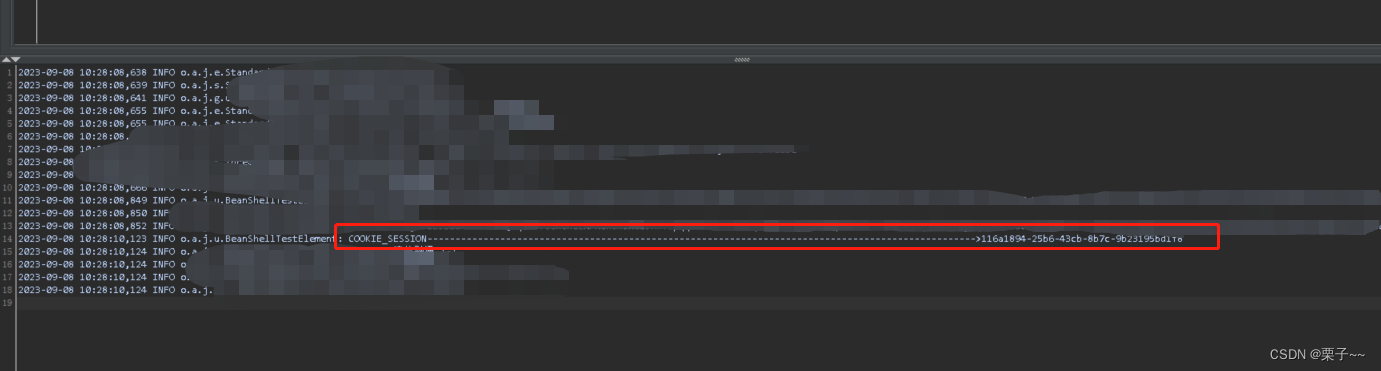
JMeter 4.0 如何获取cookie
文章目录 前言JMeter 4.0 如何获取cookie1. 修改jmeter.properties 文件2. 添加HTTP Cookie 管理器3. 获取cookie信息 前言 如果您觉得有用的话,记得给博主点个赞,评论,收藏一键三连啊,写作不易啊^ _ ^。 而且听说点赞的人每天…...
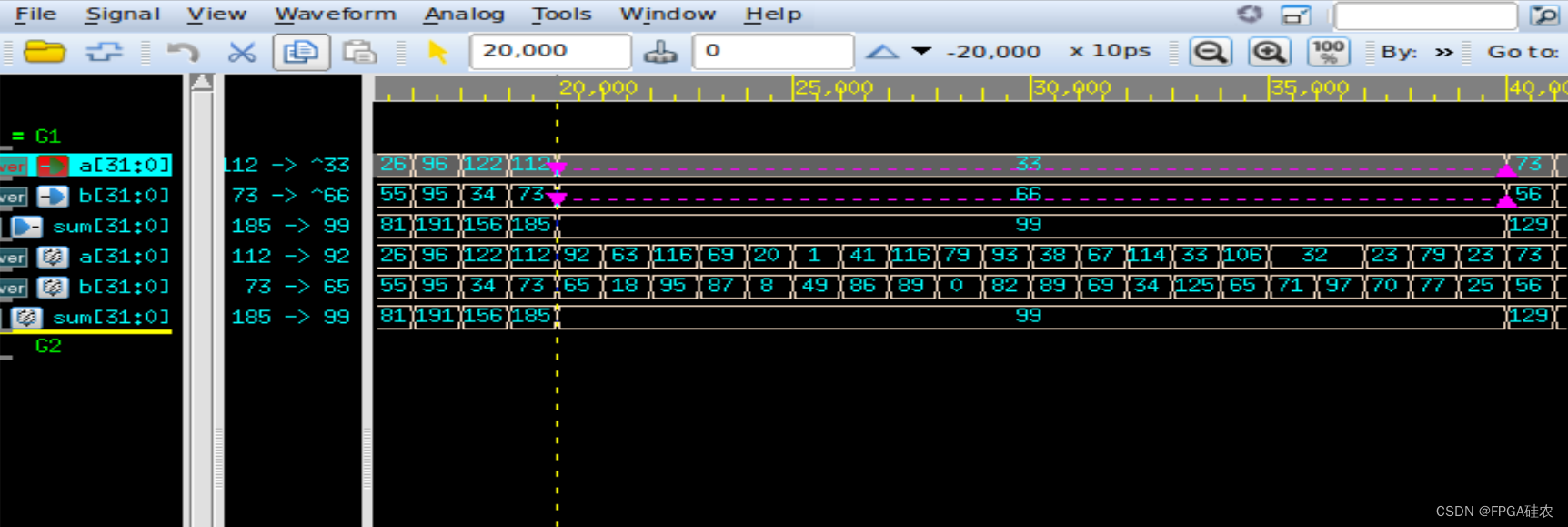
【数字IC/FPGA】Verilog中的force和release
在Verilog中,将force用于variable会覆盖掉过程赋值,或者assign引导的连续(procedural assign)赋值,直到release。 下面通过一个简单的例子展示其用法: 加法器代码 module adder ( input logic [31:0] a, …...

进阶C语言-指针的进阶(上)
指针的进阶 📖1.字符指针📖2.指针数组📖3.数组指针🎈3.1 数组指针的定义🎈3.2 &数组名VS数组名🎈3.3 数组指针的使用 📖4.数组参数、指针参数🎈4.1一维数组传参🎈4.2…...

初始化一个 vite + vue 项目
创建项目 首先使用以下命令创建一个vite项目 npm create vite然后根据提示命令 cd 到刚创建的项目目录下,使用npm install安装所需要的依赖包,再使用npm run dev即可启动项目 配置 vite.config.js 添加process.env配置,如果下面 vue-route…...

关于B+树
在数据库管理系统中,使用b树作为索引的数据结构,相比于B树和二叉树,有以下几个好处: b树的非叶子节点只存储关键字和指针,不存储数据,这样可以增加每个节点的关键字数量,降低树的高度ÿ…...

axios 请求和响应拦截器
1. 创建实例 使用 axios.create() 使用自定义配置创建一个 axios 实例。 const $http axios.create({timeout: 1000,headers: {Content-Type: application/json,} })2. 拦截器 在请求或响应被 then 或者 catch 处理前拦截他们,拦截分为请求拦截和响应拦截。 //…...

Element-ui select远程搜索
template部分: <el-form-item label"用户" prop"userId"><el-selectv-model"temp.userId"placeholder"用户"filterableremote:reserve-keyword"false":remote-method"remoteMethod":loading"loadi…...

【Express.js】Docker部署
Docker部署 本节我们来介绍如何使用 Docker 部署 express 应用 准备工作 linux 系统安装好 Docker一个基础的 evp-express-cli 项目,选上 pkg 工具包Docker 的详细用法本文不做介绍,请先自行查阅了解 在 Docker 中部署源码 一个很简单的部署方法就是…...

面试2:通用能力
15丨如何做好开场:给自我介绍加“特效 第一层,满足面试官对信息的期待 这是对自我介绍的基本要求,把个人信息、主要经历、经验和技能有条理地组织起来, 有逻辑地讲出来。需要找出多段经历的关联性和发展变化,形成连…...
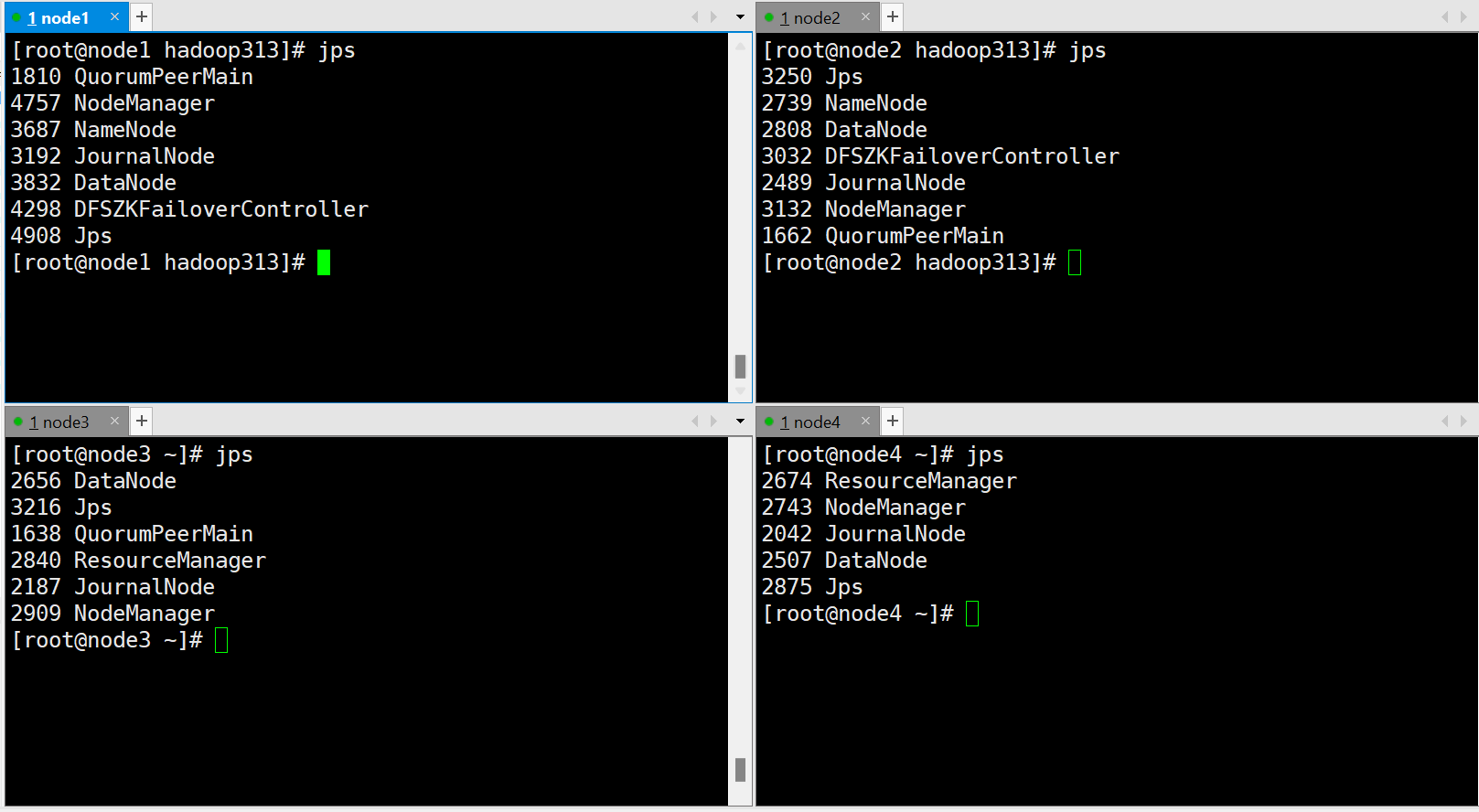
zookeeper/HA集群配置
1.zookeep配置 1.1 安装4台虚拟机 (1)按照如下设置准备四台虚拟机,其中三台作为zookeeper,配置每台机器相应的IP,hostname,下载vim,ntpdate配置定时器定时更新时间,psmiscÿ…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
