Matlab 如何选择采样频率和信号长度
Matlab 如何选择采样频率和信号长度
1、概述
在实际信号分析中经常会遇到要分辨出频率间隔为 的两个分量,在这种情形中如何选择采样频率和信号的长度呢?
2、案例分析
设有一个信号由三个正弦信号组成,其频率分别为
,即:
下面介绍如何选择采样频率 和信号长度 N 。
因为信号的最高频率为 3Hz,故按采样定理
,选择
,由频域分辨率分析可知,若要分辨 1Hz 和 2.5Hz的频率分量,最小采样长度 N1必须满足
若要区分 2.5Hz 和 3Hz 的频率分量,则最小采样长度 N2 必须为
因此,为了能区分各频率的峰值,信号的最小长度应为20。
3、实例
例:某信号由三个正弦信号组成,频率分别为,采样频率
,分别以数据长度
来分析该信号。
% Matlab 如何选择采样频率和信号长度
%
% pr2_2_10 clear; clc; close all;M = 256; % 数据长度M
fs = 10; % 采样频率fs
f1 = 1; f2 = 2.5; f3 = 3; % 设置3个正弦信号的频率
t = (0:M-1)/fs; % 设置时间序列
x = cos(2*pi*f1*t)+cos(2*pi*f2*t)+cos(2*pi*f3*t); % 计算出信号波形X1 = fft(x,20); % FFT变换
X2 = fft(x,40);
X3 = fft(x,128);
freq1 = (0:10)*fs/20; % 计算3个信号在频域的频率刻度
freq2 = (0:20)*fs/40;
freq3 = (0:64)*fs/128;% 作图
plot(freq1,abs(X1(1:11)),'g--',freq2,abs(X2(1:21)),'r:',freq3,abs(X3(1:65)),'b-');
legend('N=20','N=40','N=128');
title('不同N值的DFT变换');
xlabel('频率/Hz');
ylabel('幅值');
set(gcf,'color','w');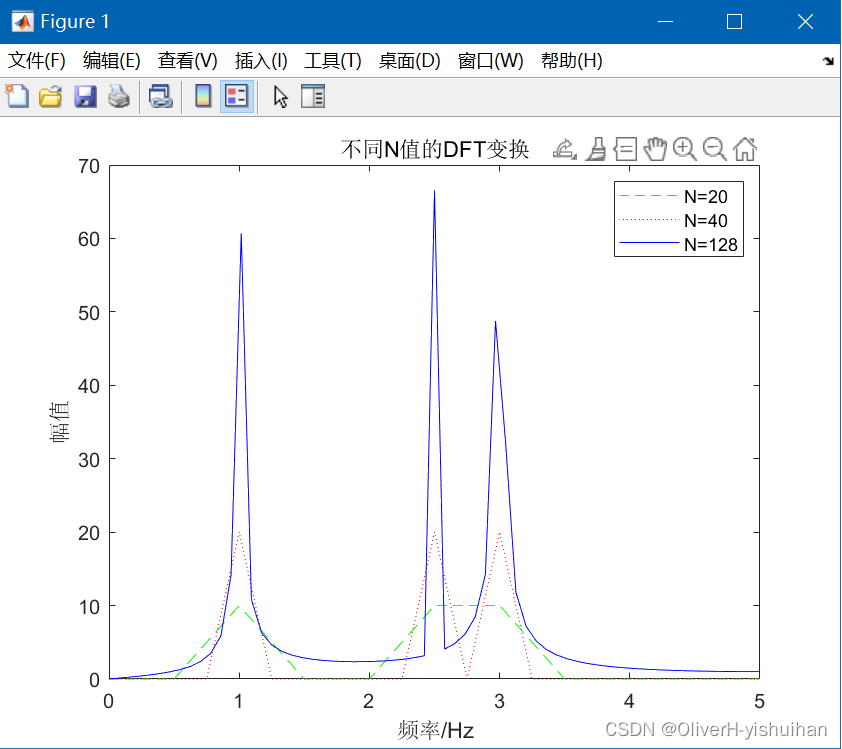
从图中可以看出,当 N=20 点时,虽然 2.5Hz 和 3Hz 这两个峰值大致能分开,但还是不太明显,可以认为是两个峰值,也可能被误认为有一个峰值在这两点之间。当 N=40 点时这两个峰值就十分明显了,因为 N 增加一倍后在这两点之间增加了一个谷值,从而突出了峰值。当 N=128 时,峰值更明显了,但由于栅栏现象和矩形窗泄漏存在,3个正弦信号虽然输入时幅值相同,但从频域上反映出的幅值各不相同。
相关文章:

Matlab 如何选择采样频率和信号长度
Matlab 如何选择采样频率和信号长度 1、概述 在实际信号分析中经常会遇到要分辨出频率间隔为 的两个分量,在这种情形中如何选择采样频率和信号的长度呢? 2、案例分析 设有一个信号由三个正弦信号组成,其频率分别为 ,即…...

TPTU: Task Planning and Tool Usage of Large Language Model-based AI Agents
本文是LLM系列文章,针对《TPTU: Task Planning and Tool Usage of Large Language Model-based AI Agents》的翻译。 TPTU:任务规划和工具使用的LLM Agents 摘要1 引言2 方法3 评估4 相关工作5 结论 摘要 随着自然语言处理的最新进展,大型语言模型&…...

【Spring IoC容器的加载过程】
加载配置文件 Spring IoC容器的配置通常以XML形式存储,并通过ResourceLoader和XmlBeanDefinitionReader类来加载。ResourceLoader主要负责加载Bean配置文件,而XmlBeanDefinitionReader则负责解析这些文件,将Bean定义封装为BeanDefinition对象…...
C++多文件类的声明与实现
...
16 “count(*)“ 和 “count(1)“ 和 “count(field1)“ 的差异
前言 经常会有面试题看到这样的问题 “ select count(*) ”, “ select count(field1) ”, “ select count(1) ” 的效率差异啥的 然后 我们这里 就来探索一下 这个问题 我们这里从比较复杂的 select count(field1) 开始看, 因为 较为复杂的处理过程 会留一下一些关键的调试…...

【云原生进阶之PaaS中间件】第一章Redis-1.4过期策略
1 设置带过期时间的 key # 时间复杂度:O(1),最常用方式 expire key seconds# 字符串独有方式 setex(String key, int seconds, String value)除了string独有设置过期时间的方法,其他类型都需依靠expire方法设置时间&a…...
windows弹出交互式服务检测一键取消bat脚本
现象 脚本命令 新建一个bat文件,将下面的脚本拷贝进去,保存,双击即可 禁用服务:重启电脑的时候不会启动 停止服务:立即停止服务,马上生效的 sc config UI0Detect start disabled net stop UI0Detect...
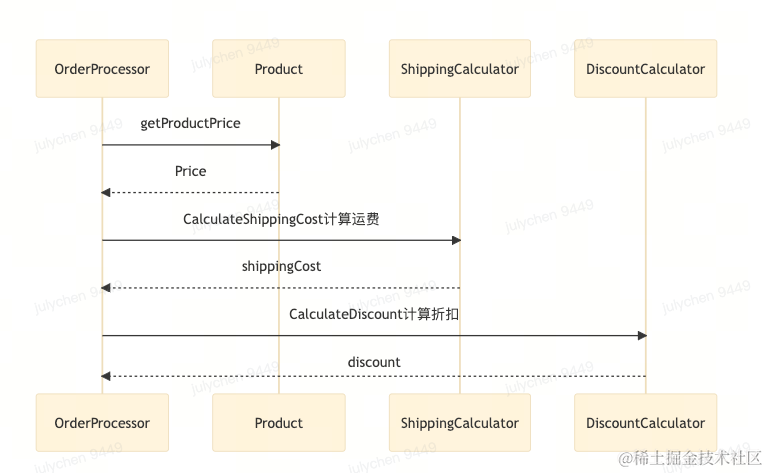
接口使用的最佳时机
1. 引言 接口在系统设计中,以及代码重构优化中,是一个不可或缺的工具,能够帮助我们写出可扩展,可维护性更强的程序。 在本文,我们将介绍什么是接口,在此基础上,通过一个例子来介绍接口的优点。…...

freertos之任务运行时间统计实验
这里写目录标题 任务时间统计函数时间统计API函数使用流程实验 任务时间统计函数 void vTaskGetRunTimeStats(char * pcWriteBuffer); 时间统计API函数使用流程 实验 1.首先现在FreeRTOSConfig.h文件里将configGENERATE_RUN_TIME_STATS 和configUSE_STATS_FORMATTING_FUNCTIO…...

Js中一些数组常用API总结
前言 Js中数组是一个重要的数据结构,它相比于字符串有更多的方法,在一些算法题中我们经常需要将字符串转化为数组,使用数组里面的API进行操作。本篇文章总结了一些数组中常用的API,我们把它们分成两类,一类是会改变原…...
LlamaIndex:将个人数据添加到LLM
推荐:使用 NSDT场景编辑器 快速搭建3D应用场景 LlamaIndex是基于大型语言模型(LLM)的应用程序的数据框架。像 GPT-4 这样的 LLM 是在大量公共数据集上预先训练的,允许开箱即用的令人难以置信的自然语言处理能力。但是,…...
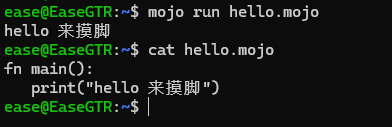
Mojo 摸脚语言,似乎已经可以安装
文章原地址:https://i.scwy.net/it/2023/090821-mojo/ Mojo 吹得很凶,面向AI编程,甩Python几十条街,融资上亿.... 但无缘一试,在Win和Ubuntu上试都不能通过。 由 LLVM 和 Swift 编程语言的联合创始人 Chris Lattner…...

Spark 6:Spark SQL DataFrame
SparkSQL 是Spark的一个模块, 用于处理海量结构化数据。 SparkSQL是用于处理大规模结构化数据的计算引擎 SparkSQL在企业中广泛使用,并性能极好 SparkSQL:使用简单、API统一、兼容HIVE、支持标准化JDBC和ODBC连接 SparkSQL 2014年正式发布,当…...

区块链智能合约编程语言 Solidity
文章目录 前言Solidity 介绍Solidity 文件结构许可声明编译指示数据类型函数事件访问区块元数据 简单的智能合约 前言 上文介绍了区块链生态发展,我们知道以太坊的到来可以使开发人员基于区块链开发DApp,本文介绍 Solidity 编程语言的使用,然…...

将SSL证书设置成HTTPS的详细步骤
在互联网上建立一个安全且可信任的网站,HTTPS是一种常用的解决方案。HTTPS是HTTP的安全版本,通过使用SSL/TLS协议对传输的数据进行加密,确保数据传输的安全性。要实现HTTPS,你需要将SSL证书设置到你的网站上。以下是详细的步骤&am…...
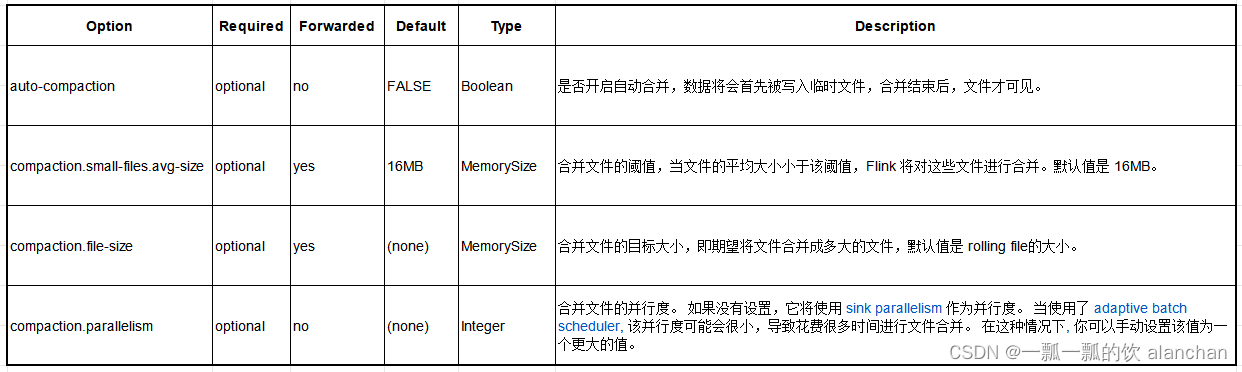
43、Flink之Hive 读写及详细验证示例
Flink 系列文章 1、Flink 部署、概念介绍、source、transformation、sink使用示例、四大基石介绍和示例等系列综合文章链接 13、Flink 的table api与sql的基本概念、通用api介绍及入门示例 14、Flink 的table api与sql之数据类型: 内置数据类型以及它们的属性 15、Flink 的ta…...

2023数模国赛C 题 蔬菜类商品的自动定价与补货决策-完整版创新多思路详解(含代码)
题目简评:看下来C题是三道题目里简单一些的,考察的点比较综合,偏数据分析。涉及预测模型和运筹优化(线性规划),还设了一问开放型问题,适合新手入门,发挥空间大。 题目分析与思路: 背景&#x…...
javaScript:DOM中常用尺寸
目录 前言(可以根据图示找到需要的尺寸,便于理解) 内尺寸 clientWidth 包含左右padding和宽度width(忽略滚动条的宽度) clientHeight 包含上下padding和height(忽略滚动条的高度) clientTo…...
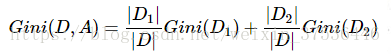
决策树算法学习笔记
一、决策树简介 首先决策树是一种有监督的机器学习算法,其采用的方法是自顶向下的递归方法,构建一颗树状结构的树,其具有分类和预测功能。其基本思想是以信息熵为度量构造一棵熵值下降最快的树,到叶子节点处的熵值为零。决策树的构…...

Verilog_mode常用的几个用法
一:verilog mode中如何使用正则表达 在顶层实例化时,有大量的信号需要重新命名,使用模板的话会增加大量的注释内容,不过往往这些信号命名有特定的规律,我们可以使用正则表达式来处理,下面举几个例子&#…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...
