AI将如何影响程序员的未来,以及如何不被AI所替代。
随着人工智能技术的不断发展,越来越多的工作被自动化和智能化所取代,其中程序员这个职业也不例外。然而,我们需要客观地分析AI在未来对程序员的影响,并且给出建议,以便程序员能够保持竞争力,不被AI所取代。
以下是我的一些看法:
一、AI对程序员的影响
-
自动化开发工具的出现
随着人工智能技术的不断进步,自动化开发工具也越来越多,例如模板代码生成工具、自动化测试工具、智能调试工具等。这些工具可以大大提高开发效率,节省人力成本。 -
机器学习的发展
随着机器学习的发展,越来越多的应用场景需要程序员具备一定的机器学习知识,例如智能推荐系统、智能客服等。这意味着程序员需要不断学习和更新自己的技能。 -
AI在软件开发生命周期中的应用
AI可以在软件开发的各个阶段中发挥作用,例如需求分析、设计、编码、测试、维护等。在未来,越来越多的软件开发工作将会交给AI来完成。 -
职业前景的变化
随着自动化和智能化的进步,一些传统的程序员职位可能会逐渐消失,而一些新兴的职位将会逐渐兴起,例如AI工程师、数据科学家等。
二、如何不被AI替代
-
持续学习和更新知识
随着技术的不断发展,程序员需要不断学习和更新自己的知识,掌握新的技术和工具。只有保持持续的学习和更新,才能不被AI所取代。 -
关注新技术和新兴领域
程序员需要关注新技术和新兴领域的发展,例如机器学习、人工智能、大数据等。只有掌握这些新技术和新兴领域的知识,才能在未来的竞争中保持竞争力。 -
提高沟通能力和团队合作能力
随着自动化和智能化的发展,程序员需要与其他领域的专业人员进行更加密切的合作。因此,程序员需要提高自己的沟通能力和团队合作能力,以更好地完成工作任务。 -
建立自己的个人品牌
建立自己的个人品牌可以帮助程序员在未来的竞争中脱颖而出。通过在社交媒体上发布自己的文章和代码,参与开源项目和技术社区,以及参加各种技术会议和活动,程序员可以提高自己的知名度和影响力。 -
发掘自己的特长和潜力
程序员应该发掘自己的特长和潜力,找到自己擅长的领域,并不断深入学习和发展。例如,一些程序员可能更加擅长数据科学和机器学习,而另一些程序员可能更加擅长软件架构和设计。只有发掘自己的特长和潜力,才能在未来的竞争中脱颖而出。 -
保持创新精神和开放心态
程序员需要保持创新精神和开放心态,不断寻找和探索新的技术和方法。只有保持创新精神和开放心态,才能在未来的竞争中保持领先地位。
三、结论
总的来说,AI对程序员职业的影响是不可避免的。随着技术的不断进步,程序员需要不断学习和更新自己的知识,掌握新的技术和工具。只有保持持续的学习和更新,才能不被AI所取代。此外,程序员还需要关注新技术和新兴领域的发展,提高沟通能力和团队合作能力,建立自己的个人品牌,发掘自己的特长和潜力,保持创新精神和开放心态。只有这样,程序员才能在未来的竞争中保持竞争力,不被AI所替代。
那么最后,这篇文章是不是AI写的呢?
相关文章:

AI将如何影响程序员的未来,以及如何不被AI所替代。
随着人工智能技术的不断发展,越来越多的工作被自动化和智能化所取代,其中程序员这个职业也不例外。然而,我们需要客观地分析AI在未来对程序员的影响,并且给出建议,以便程序员能够保持竞争力,不被AI所取代。…...

nginx 常用配置之 pass_proxy
大家好,我是 17。 今天和大家聊聊 pass_proxy 代理。 pass_proxy 代理 在前端代理主要是为了跨域。虽然前端跨域有多种方法,各有利弊,但用代理来跨域对开发是最友好的。用代理可以不用修改产品代码切换线上线下,非常安全。pass…...

Linux中驱动模块加载方法分析
如何管理驱动模块 由于Linux驱动模块众多,系统对模块加载顺序有要求,一些基础模块在系统启动时需要很早就被加载;开发者加入自己的模块时,需要维护一个模块初始化列表,上面两方面的做起来很困难,为了科学地…...

yarn 通过 resolutions,指定子孙依赖包版本号,解决froala-editor 版本问题
前端开发项目过程中会使用到各种依赖包。但是这些依赖包虽然好用,但是一味使用最新版本可能会出现各种奇葩问题,因此我们经常会针对一些依赖包指定一个稳定版本。 常用版本 版本号注释“1.0.2”必须切到1.0.2版“>1.0.2”必须大于1.0.2版“>1.0.…...
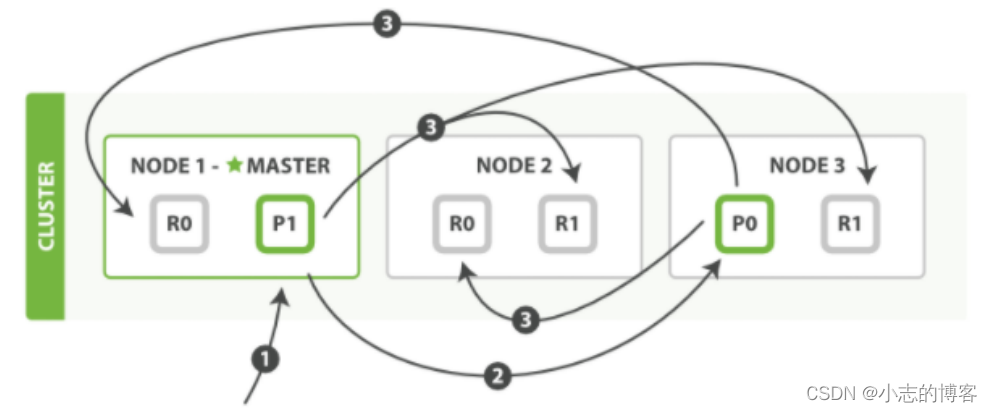
Elasticsearch7.8.0版本进阶——多文档操作流程
目录一、多文档操作1.1、多文档操作的概述1.2、多文档操作与单文档模式区别二、用单个 mget 请求取回多个文档2.1、用单个 mget 请求取回多个文档的图解2.2、用单个 mget 请求取回多个文档的步骤三、bulk API 的模式请求取回多个文档3.1、bulk API 的模式请求取回多个文档的图解…...
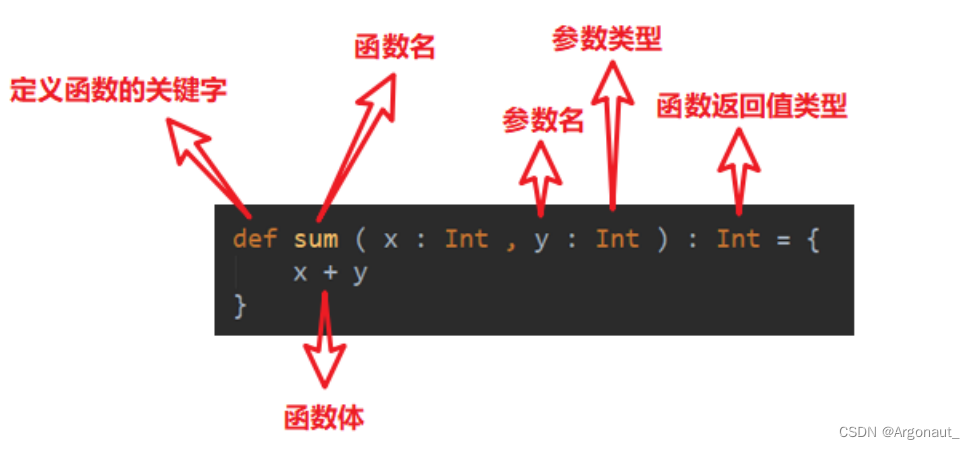
Scala函数式编程(第五章:函数基础、函数高级详解)
文章目录第 5 章 函数式编程5.1 函数基础5.1.1 函数基本语法5.1.2 函数和方法的区别5.1.3 函数定义5.1.4 函数参数5.1.5 函数至简原则(重点)5.2 函数高级5.2.1 高阶函数5.2.2 匿名函数5.2.3 高阶函数案例5.2.4 函数柯里化&闭包5.2.5 递归5.2.6 控制抽…...

ZED相机快速使用指南
1、安装SDK ZED SDK 3.8 - Download | Stereolabs 2、安装ros GitHub - stereolabs/zed-ros-wrapper: ROS wrapper for the ZED SDK 其他教程:ZED2相机SDK安装使用及ROS下使用_可即的博客-CSDN博客 3、官方文档 Get Started with ZED | Stereolabs 4、标定参…...
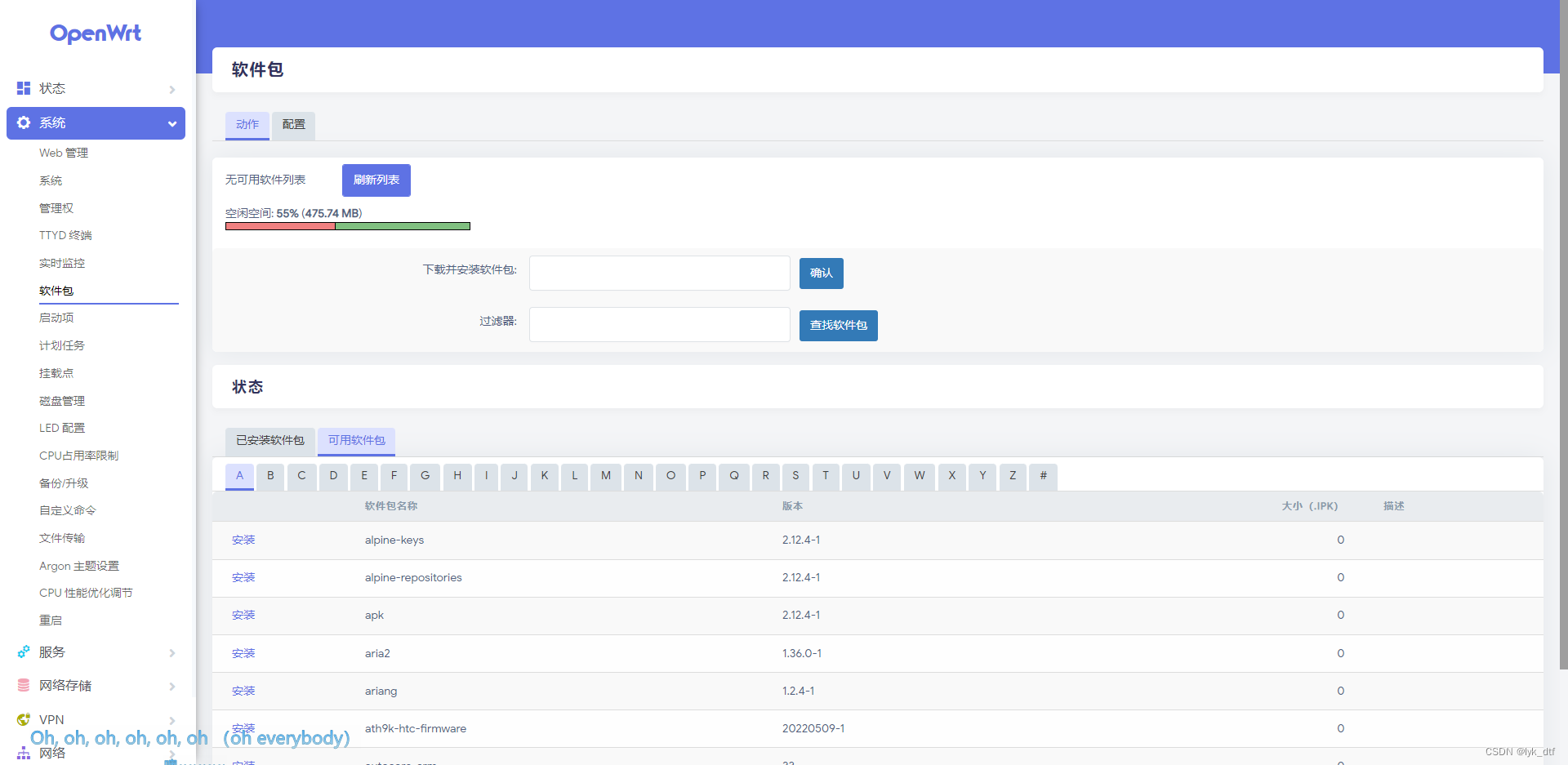
树莓派4b配置OpenWrt联网
文章目录前言一、下载固件二、配置wan口三、简单介绍1、修改无线名称、设置密码2、下载软件包总结前言 树莓派4b内置wifi模块,加一个千兆网口 好像有一种办法,通过无线wifi链接其他wifi通网,然后把这个网口作为lan口,连接电脑使…...

不同语言下的定时器,你都掌握了吗?
我们大家都对定时器不陌生,无论是现实中还是项目中,都离不开定时。在现实中,它叫闹钟,在项目上,它叫定时器,即定时触发某件事情。它能帮助我们在某一个既定的时间节点上,来提醒我们做一些事情&a…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 水仙花数(Python) | 机试题+算法思路+考点+代码解析 【2023】
水仙花数 题目 所谓的水仙花数是指一个n位的正整数其各位数字的n次方的和等于该数本身, 例如153 = 1^3 + 5^3 + 3^3,153是一个三位数 输入 第一行输入一个整数N, 表示 N 位的正整数 N 在3-7之间包含3,7 第二行输入一个正整数M, 表示需要返回第M个水仙花数 输出描述 返…...

在onBindViewHolder设置View的translation失败或错乱的问题
这个问题,可以换成“为什么在onCreate里面修改一些子View不生效,错位,乱”等问题。 本质原因肯定是在没有把整个ViewGroup渲染完成之前,操作了部分子View,导致了位置偏移等。 解决办法也很简单,通过调用Vi…...

【2.21】MySQL索引、动态规划、学习方法
索引常见面试题 什么是索引 索引的定义就是帮助存储引擎快速获取数据的一种数据结构,形象的说就是索引是数据的目录。存储引擎,说白了就是如何存储数据、如何为存储的数据建立索引和如何更新、查询数据等技术的实现方法。索引和数据就是位于存储引擎。…...
| 包含代码编写思路)
华为OD机试题 - 二叉树层次遍历(JavaScript)| 包含代码编写思路
最近更新的博客 华为OD机试题 - 字符串加密(JavaScript) 华为OD机试题 - 字母消消乐(JavaScript) 华为OD机试题 - 字母计数(JavaScript) 华为OD机试题 - 整数分解(JavaScript) 华为OD机试题 - 单词反转(JavaScript) 华为OD机试题 最近更新的博客使用说明二叉树层次遍…...

力扣解法汇总1140. 石子游戏 II
目录链接: 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接:力扣 描述: 爱丽丝和鲍勃继续他们的石子游戏。许多堆石子 排成一行,每堆都有正整…...

Kerberos认证原理与使用教程
Kerberos认证原理与使用教程 一、Kerberos 概述 二、什么是 Kerberos Kerberos 是一种计算机网络认证协议,用来在非安全网络中,对个人通信以安全的手段进行身份认证。这个词又指麻省理工学院为这个协议开发的一套计算机软件。软件设计上采用客户端…...
内存取证常见例题思路方法-volatility (没有最全 只有更全)
目录 1.从内存文件中获取到用户hacker 的密码并且破解密码,将破解后的密码作为 Flag值提交; 2.获取当前系统的主机名,将主机名作为Flag值提交; 3.获取当前系统浏览器搜索过的关键词,作为Flag提交; 4.获取当前内存文件的 ip地址 5.当前系…...
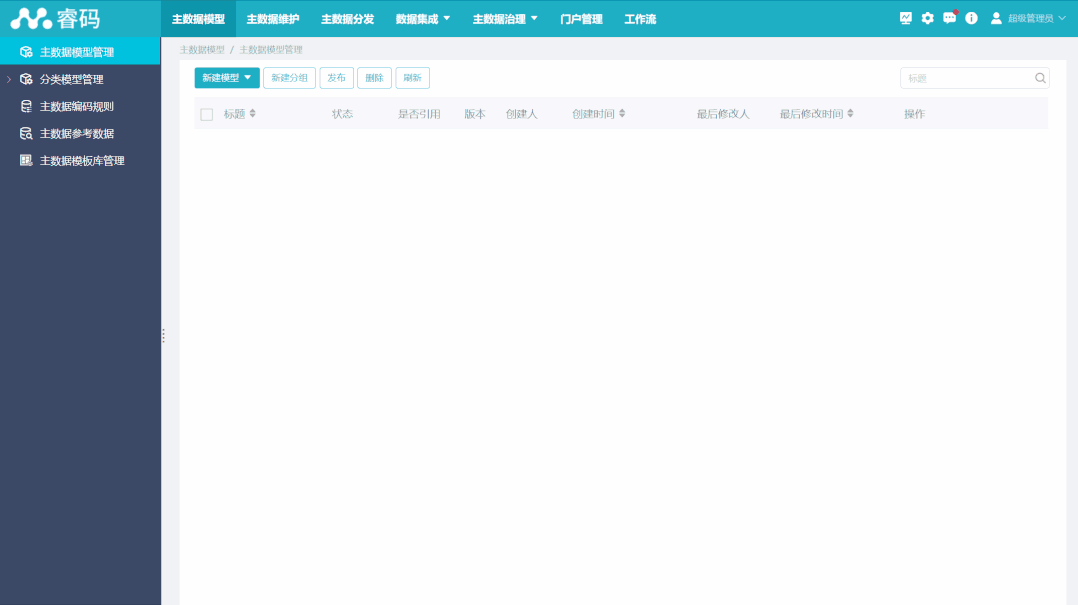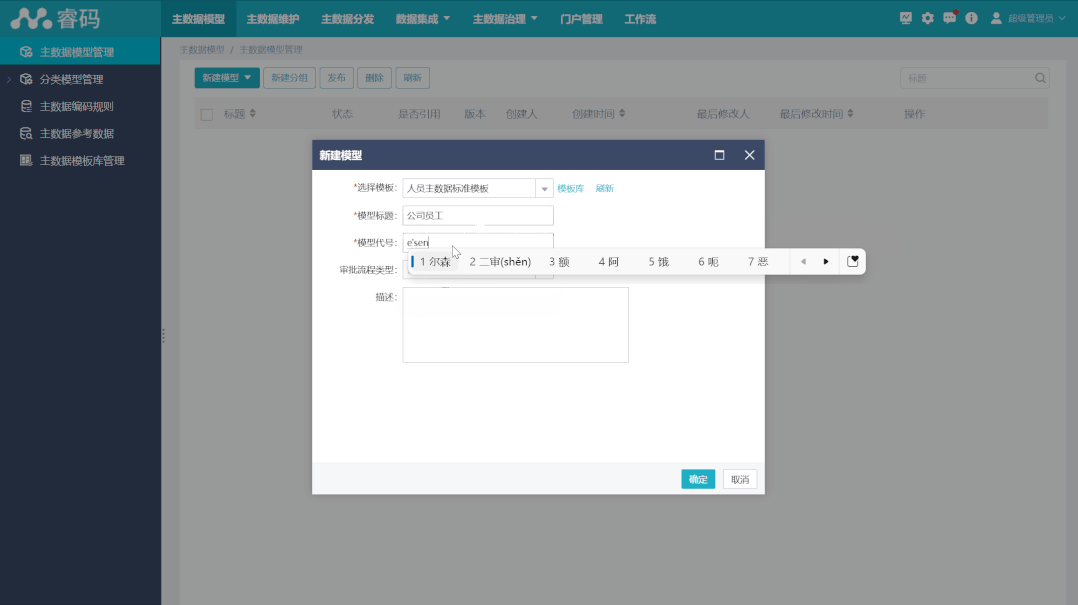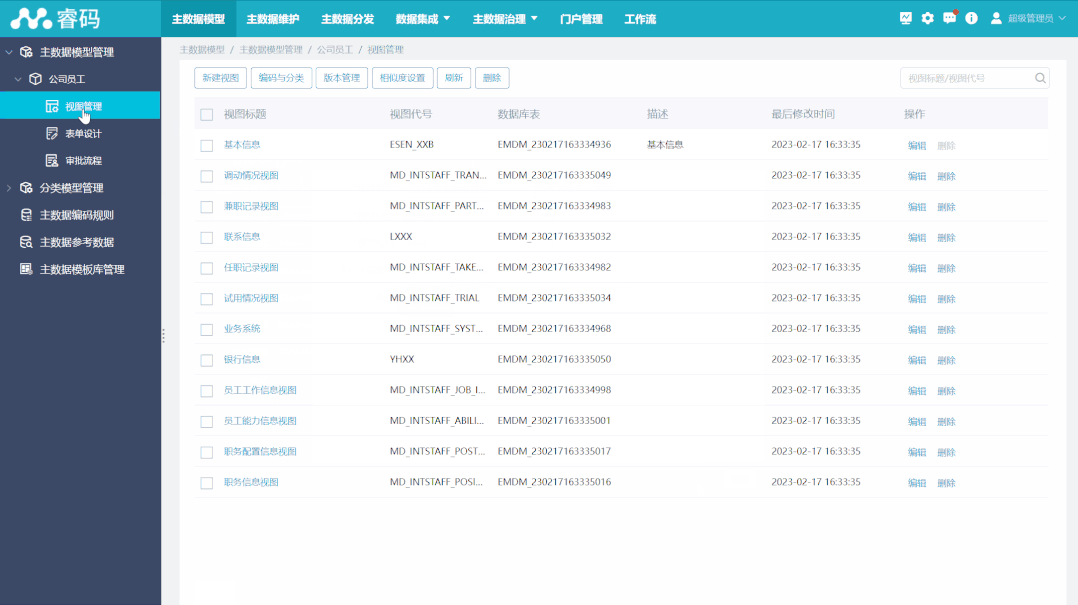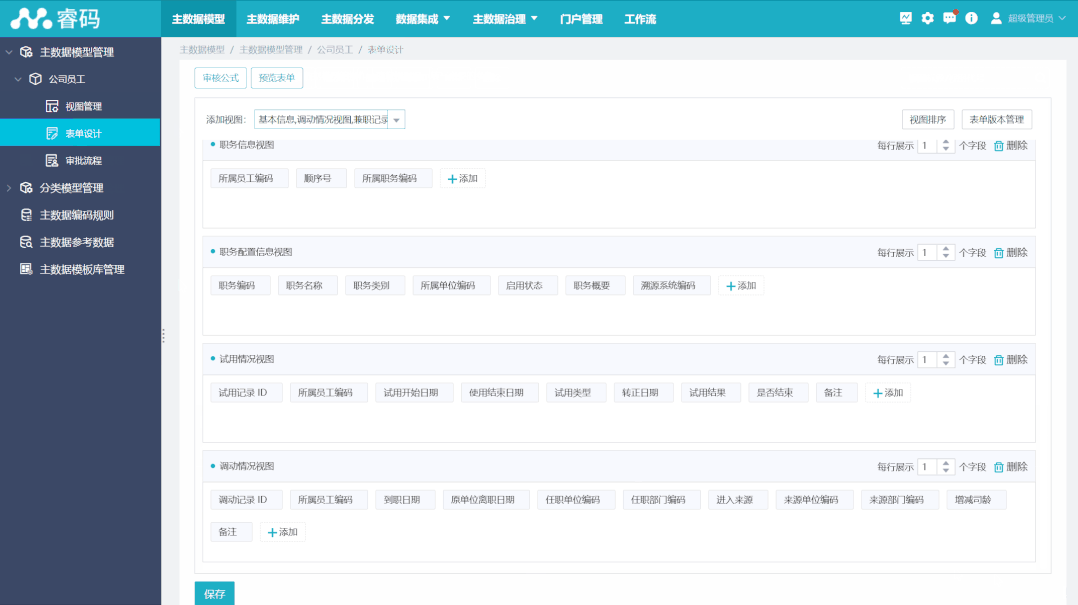
10 种主数据模型设计示例分享,推荐收藏
主数据模型是主数据管理的基础,一个完整的、可扩展的、相对稳定的主数据模型对于主数据管理的成功起着重要的作用。规划、创建主数据模型的过程,是梳理主数据管理体系的过程,目的是建立一个良好的资源目录结构,划分合理的资源粒度…...

React学习笔记
React学习笔记 概述 React是用于构建用户界面的JavaScript库。 现在前端领域最为流行的三大框架: VueReactAngular 其中,Vue和React是国内最为流行的两个框架。 React的特点: 1、声明式编程:它允许我们只需要维护自己的状态…...
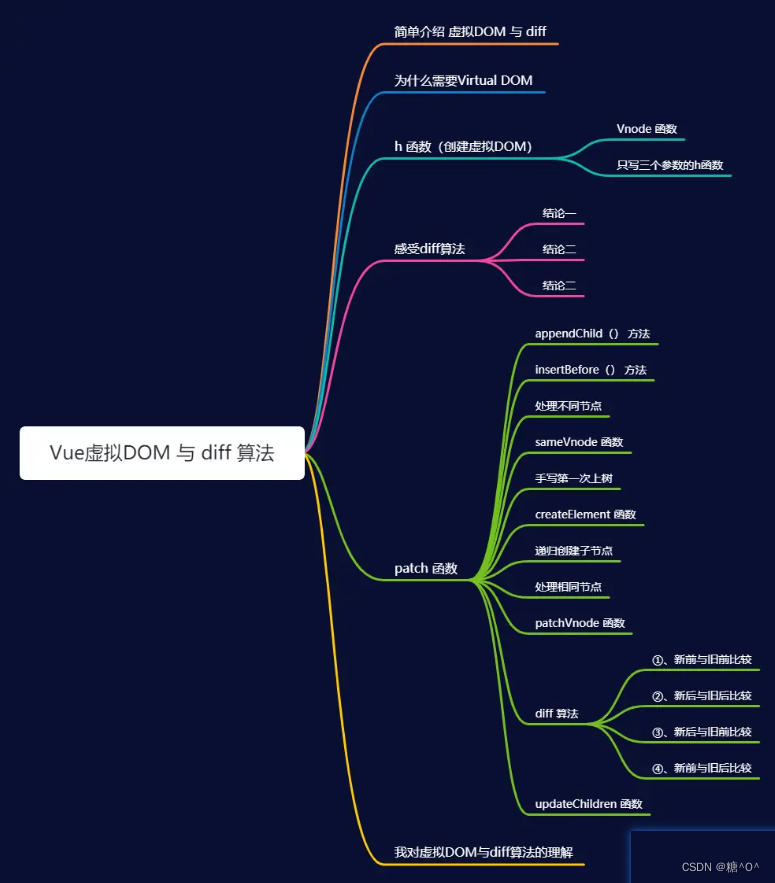
【Vue源码解析】Vue虚拟dom和diff算法
Vue虚拟dom和diff算法1. 简介2. 搭建环境1. 安装snabbdom2. 安装webpack5并配置3、函数3.1 虚拟节点vnode的属性3.2 使用h函数 创建虚拟节点3.3 使用patch函数 将虚拟节点上DOM树3.4 h函数嵌套使用,得到虚拟DOM树(重要)3.5 patchVnode函数3.6…...

算法学习与填充计划---2023.2.21---夏目
🚀write in front🚀 📝个人主页:认真写博客的夏目浅石.CSDN 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:ACM周训练题目合集.CSDN 💬总结:…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
