洛谷P8814:解密 ← CSP-J 2022 复赛第2题
【题目来源】
https://www.luogu.com.cn/problem/P8814
https://www.acwing.com/problem/content/4732/
【题目描述】
给定一个正整数 k,有 k 次询问,每次给定三个正整数 ni,ei,di,求两个正整数 pi,qi,使 ni=pi×qi,ei×di=(pi−1)(qi−1)+1。
【输入格式】
第一行一个正整数 k,表示有 k 次询问。
接下来 k 行,第 i 行三个正整数 ni,di,ei。
【输出格式】
输出 k 行,每行两个正整数 pi,qi 表示答案。
为使输出统一,你应当保证 pi≤qi。
如果无解,请输出 NO。
【输入样例】
10
770 77 5
633 1 211
545 1 499
683 3 227
858 3 257
723 37 13
572 26 11
867 17 17
829 3 263
528 4 109
【输出样例】
2 385
NO
NO
NO
11 78
3 241
2 286
NO
NO
6 88
【数据范围】
以下记 m=n−e×d+2。
保证对于 100% 的数据,1≤k≤10^5,对于任意的 1≤i≤k,1≤ni≤10^18,1≤ei×di≤10^18,1≤m≤10^9。
【算法分析】
(1)已知 ed=(p−1)(q−1)+1=pq−p−q+1+1,又已知 n=pq,可得 ed=n−p−q+2,即 p+q=n-ed+2。若记 m=n-ed+2,则 ;
(2)又由 (p+q)^2=p^2+2pq+q^2, (p-q)^2=p^2-2pq+q^2,可得
(p+q)^2-(p-q)^2=(p^2+2pq+q^2)-(p^2-2pq+q^2)=4pq,即 (p−q)^2=(p+q^)2−4pq,开根号得,即
(3)联立可得,。同时,根据题目要求,p、q 必须是正整数,若令
,则当 ((m+t)%2==1 || (m-t)%2==1 || m<=t) 时,无解。
【算法代码】
#include<bits/stdc++.h>
using namespace std;typedef long long LL;
LL k,n,d,e;int main() {cin>>k;while(k--) {cin>>n>>d>>e;LL m=n-d*e+2;LL k=m*m-4*n;LL t=sqrt(k);if(t*t!=k) {cout<<"NO"<<endl;continue;}if((m+t)%2==1 || (m-t)%2==1 || m<=t) {cout<<"NO"<<endl;continue;}cout<<(m-t)/2<<" "<<(m+t)/2<<endl;}return 0;
}/*
in:
10
770 77 5
633 1 211
545 1 499
683 3 227
858 3 257
723 37 13
572 26 11
867 17 17
829 3 263
528 4 109out:
2 385
NO
NO
NO
11 78
3 241
2 286
NO
NO
6 88
*/
【参考文献】
https://www.luogu.com.cn/problem/solution/P8814
相关文章:
洛谷P8814:解密 ← CSP-J 2022 复赛第2题
【题目来源】https://www.luogu.com.cn/problem/P8814https://www.acwing.com/problem/content/4732/【题目描述】 给定一个正整数 k,有 k 次询问,每次给定三个正整数 ni,ei,di,求两个正整数 pi,qi…...
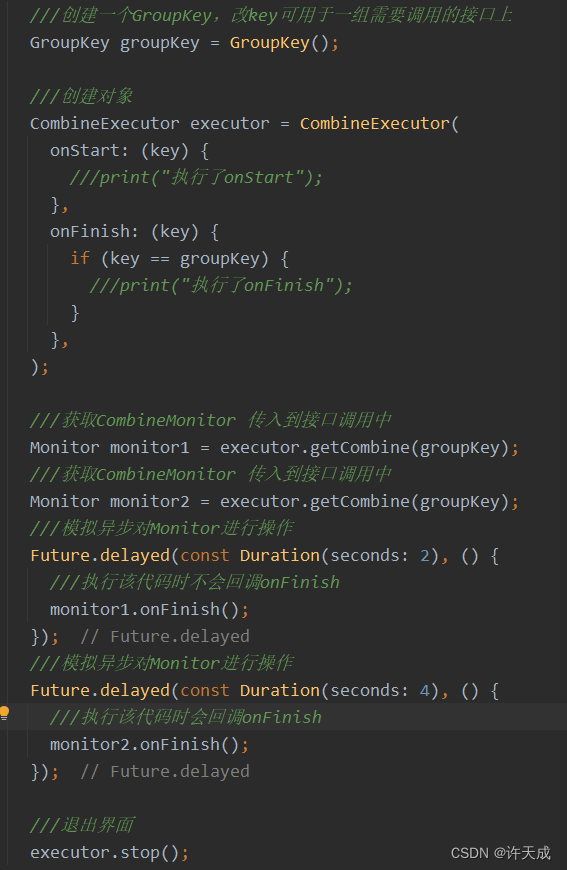
Flutter实现CombineExecutor进行多个异步分组监听,监听第一个异步执行的开始和最后一个异步执行结束时机。
1.场景 我们在调用接口时,很多时候会同时调用多个接口,接口都是异步执行,我们很难知道调用的多个接口哪个会最后执行完成,我们有时候需要对最后一个接口执行完成的时机监听,所以基于该需求,设计了CombineE…...

2023 年最新Java 毕业设计选题题目参考,500道 Java 毕业设计题目,值得收藏
大家好,我是程序员徐师兄,最近有很多同学咨询,说毕业设计了,不知道选怎么题目好,有哪些是想需要注意的。 确实毕设选题实际上对很多同学来说一个大坑, 每年挖坑给自己跳的人太多太多,选题选得好…...
Mac电脑其他文件占用超过一大半的内存如何清理?
mac的存储空间时不时会提示内存已满,查看内存占用比例最大的居然是「其他文件」,「其他文件」是Mac无法识别的格式文件或应用插件扩展等等...如果你想要给Mac做一次彻底的磁盘空间清理,首当其冲可先对「其他文件」下手,那么我们该…...

geopandas 笔记: datasets 数据集
geopandas 自带的几个数据集 1 世界各个国家 import geopandas as gpd import pandas as pdpd.set_option(display.max_rows,None) gpd.read_file(gpd.datasets.get_path(naturalearth_lowres)) pop_est人口数量continent国家所在的大陆name国家的名称iso_a3国家的三个字母的…...

长胜证券:三大拐点共振 看好智能驾驶新一轮行情
摘要 【长胜证券:三大拐点共振 看好智能驾驭新一轮行情】长胜证券研报指出,全球共振,国内智驾商场正迎来三大拐点:1)技能上,“BEV Transformer数据闭环”新架构2023年开端上车,使得不依靠高精地…...
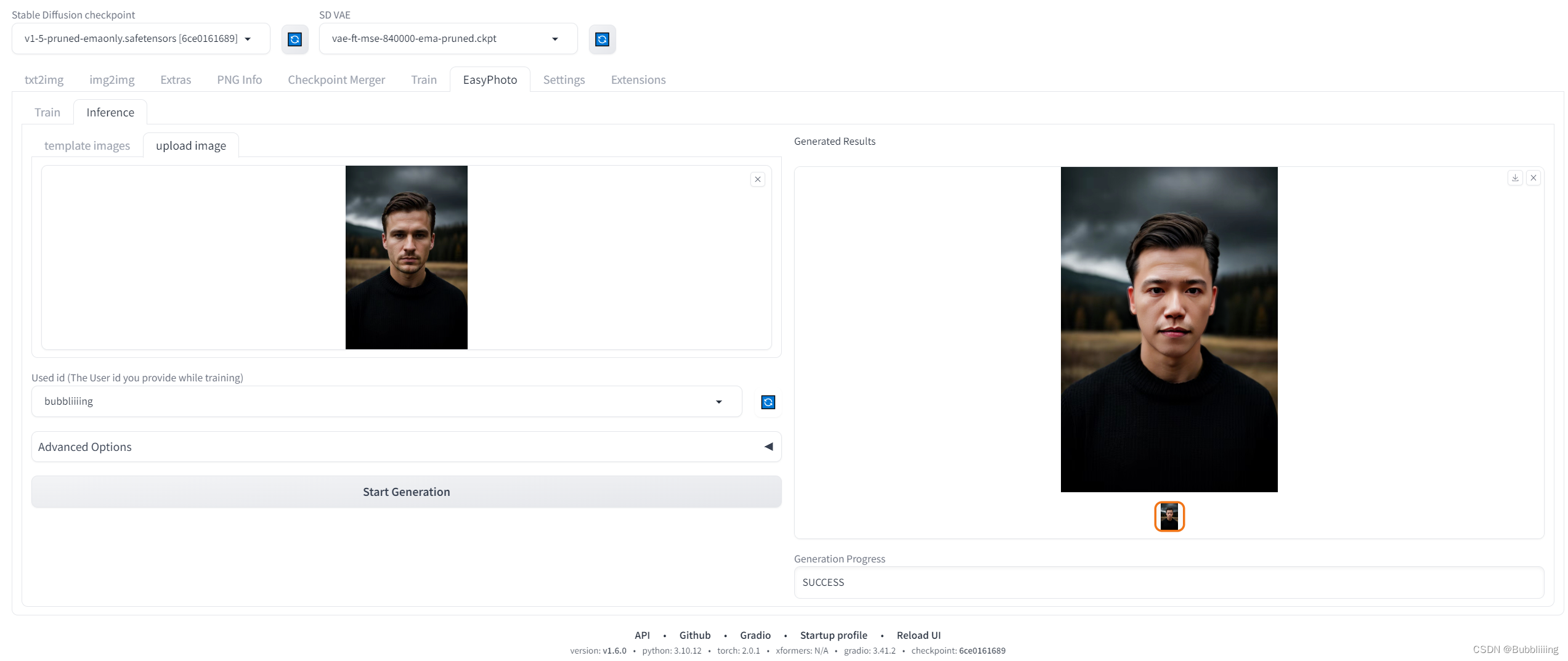
AIGC专栏5——EasyPhoto AI写真照片生成器 sd-webui插件介绍、安装与使用
AIGC专栏5——EasyPhoto AI写真照片生成器 插件安装与使用 学习前言源码下载地址技术原理储备(SD/Control/Lora)StableDiffusionControlNetLora EasyPhoto插件简介EasyPhoto插件安装安装方式一:Webui界面安装 (需要良好的网络&…...

【Python程序设计】 工厂模式【07/8】
一、说明 我们探索数据工程中使用的设计模式 - 软件设计中常见问题的可重用解决方案。 以下文章是有关 Python 数据工程系列文章的一部分,旨在帮助数据工程师、数据科学家、数据分析师、机器学习工程师或其他刚接触 Python 的人掌握基础知识。 迄今为止,…...

PHP8的多维数组-PHP8知识详解
今天分享的是php8的数组中的多维数组,主要内容有:多维数组的概念、创建和输出二维数组、创建和输出三维数组。 1、多维数组的概念 多维数组是包含一个或多个数组的数组。在多维数组中,主数组中的每一个元素也可以是一个数组,子数…...
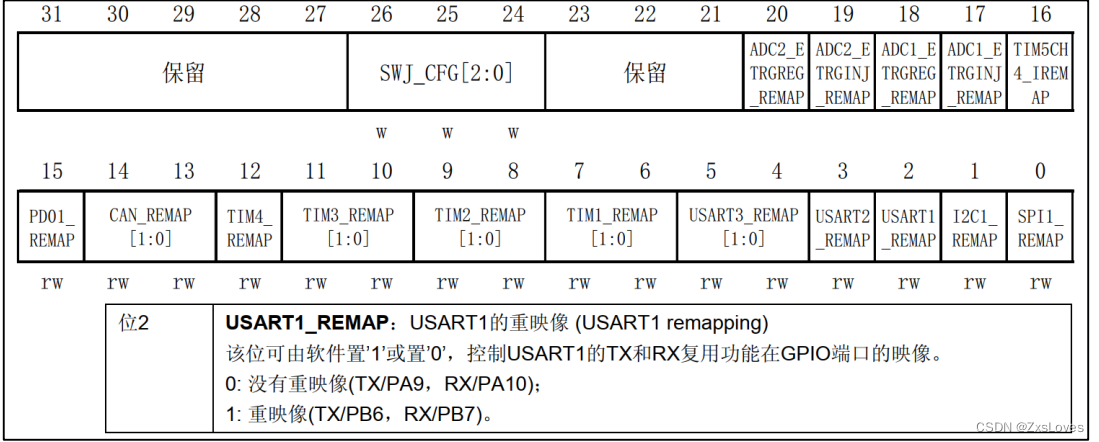
【【STM32--28--IO引脚的复用功能】】
STM32–28–IO引脚的复用功能 STM32的IO复用功能 何为复用? 我们先了解一下何为通用 IO端口的输入或输出是由GPIO外设控制,我们称之为通用 复用: IO端口的输入或者是输出是由其他非GPIO外设控制就像经常说的USART 由 DR寄存器进行输出 STM32的IO复用功…...

CodeJock Active-X / COM v22.1.0 Crack
CodeJock Active-X / COM v22.1.0--这个支持 Unicode 啦, Unicode Unicode 创建专业应用程序,其中包含一整套高度可定制的用户界面组件,包括 Visual Studio 风格的对接窗格和 Office 风格的功能区、工具栏和菜单,为您的应用程序…...

mac通过docker搭建elasticsearch:8.9.2以及kibana:8.9.2
1.elasticsearch.yml配置修改: cluster.name: "docker-cluster" network.host: 0.0.0.0 http.port: 9200 #discovery.seed_hosts: ["172.17.0.2"]#----------------------- BEGIN SECURITY AUTO CONFIGURATION ----------------------- # # T…...

python实现排列组合代码
def combination(n, c, com1, limit0, per[]):for pos in range(limit, n):t per [pos]if len(set(t)) len(t):if len(t) c:yield [pos, ]else:for result in combination(n, c, com, com * pos, per [pos, ]):yield [pos, ] resultprint("排列:") …...

盲盒小程序开发方案
盲盒游戏作为一种富有趣味性和收藏价的虚拟盲盒产品,近年来在游戏市场中备受关注。本文将深入探讨盲盒游戏的开发方案,从市场趋势分析、用户体验设计、商业模式选择等多个维度,为开发者提供业且有深度的思考,以帮助他们在盲盒游戏…...

Mysql锁
文章目录 1. 概述2. 分类3. 全局锁4. 表级锁5. 行级锁 1. 概述 锁是计算机协调多个进程或线程并发访问某一资源的机制。在数据库中,除传统的计算资源(CPU、RAM、I/O)的争用以外,数据也是一种供许多用户共享的资源。如何保证数据并…...

Kubernetes(k8s)安装NFS动态供给存储类并安装KubeSphere
Kubernetes安装NFS动态供给存储类并安装KubeSphere KubeSphere介绍环境准备KubeSphereNFS动态供给 安装NFS动态供给搭建NFS下载动态供给驱动修改驱动文件安装动态供给 安装KubeSphere下载KubeSphere的yaml资源清单文件安装KubeSphere 使用KubeSphere部署应用创建项目部署MySQL …...

机器学习笔记 - 【机器学习案例】基于KerasCV的预训练模型自定义多头+多标签预测
一、KerasCV KerasCV 是一个模块化计算机视觉组件库,可与 TensorFlow、JAX 或 PyTorch 原生配合使用。这些模型、层、指标、回调等基于Keras Core构建,可以在任何框架中进行训练和序列化,并在另一个框架中重复使用,而无需进行昂贵的迁 KerasCV 可以理解为 Keras API 的水平…...

Linux Debian常用70条经典运维命令和使用案例
一、前言 今天分享一些Linux Debian运维方法以及常用命令 二、运维方法 Linux Debian系统的运维涉及到各种任务,包括系统安装、配置、更新和维护,以及故障排查和性能优化等。下面是一些常用的运维命令: 1、以下是部分命令注释 1. apt-ge…...

【涵子来信】——步入中学,日积跬步,以致千里
大家好: 我是涵子,好久没有发文,今天发个文。 如果说,给你一次再入中学的机会,你会怎么想?对于刚刚步入中学的我,目前状况尚好,洛谷最近刷得紧,看看我的洛谷。 好的&…...
【sgCreateAPI】自定义小工具:敏捷开发→自动化生成API接口脚本(接口代码生成工具)
<template><div :class"$options.name"><div class"sg-head">接口代码生成工具</div><div class"sg-container"><div class"sg-start "><div style"margin-bottom: 10px;">接口地…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
