MATLAB实现函数拟合
目录
一.理论知识
1.拟合与插值的区别
2.几何意义
3.误差分析
二.操作实现
1.数据准备
2.使用cftool——拟合工具箱
三.函数拟合典例
四.代码扩展
一.理论知识
1.拟合与插值的区别
通俗的说,插值的本质是根据现有离散点的信息创建出更多的离散点,从而不断提高精度;而拟合则不需要找到更多的点,目标在于根据已知的点构造出一条函数,使得每点上的误差尽可能地低——即曲线拟合的最好(最小化损失函数)。

2.几何意义
本质来说,就是尽可能找到——能经过当前全部点且误差最小的曲线。

理论部分这里不细说,涉及到最小二乘法,大家自行查资料~
3.误差分析

二.操作实现
1.数据准备
| x | 4.2 | 5.9 | 2.7 | 3.8 | 3.8 | 5.6 | 6.9 |
| y | 8.4 | 11.7 | 4.2 | 6.1 | 7.9 | 10.2 | 13.2 |
| x | 3.5 | 3.6 | 2.9 | 4.2 | 6.1 | 5.5 | 6.6 |
| y | 6.6 | 6 | 4.6 | 8.4 | 12 | 10.3 | 13.3 |
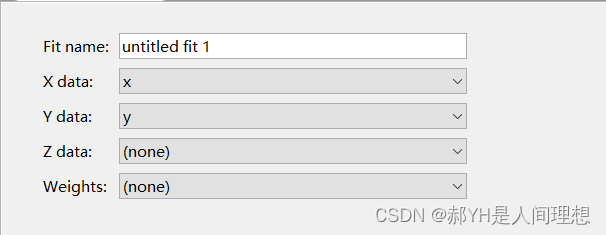
2.使用cftool——拟合工具箱
如上图,在APP菜单栏中找到“Curve Fitting”打开工具箱,或者在命令行输入:
cftool
在工具箱页面的左上角,选择x与y对应的变量。
然后右下角就会出现函数图像,这是未拟合前的默认形态。
然后即可选择拟合方式,通常情况下多项式拟合即可得到不错的效果。
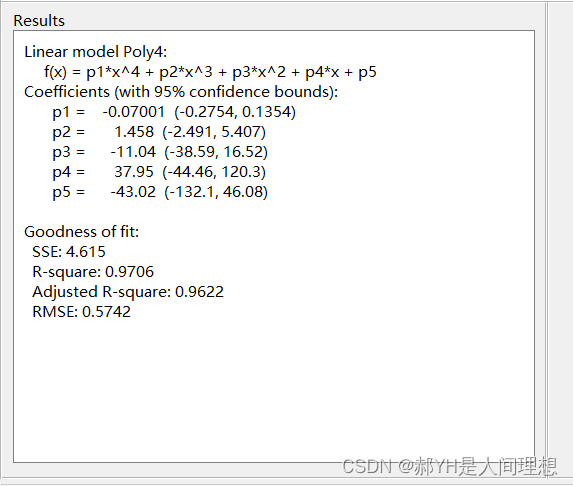
如上图,即为4次多项式拟合的效果。
如上是有关拟合误差的一些数据,需要重点关注的是:
- R值——拟合优度:当R值大于0.9或0.95时,即可认为拟合出来的函数可信度很高。
- 另外SSE等有关残差的参数也可以注意一下
左下角给出了一些拟合结果的内容,如上图可知:
y=-0.07001*x^4+1.458*x^3-11.04*x^2+37.95*x-43.02,即为本次拟合出的函数方程!
三.函数拟合典例
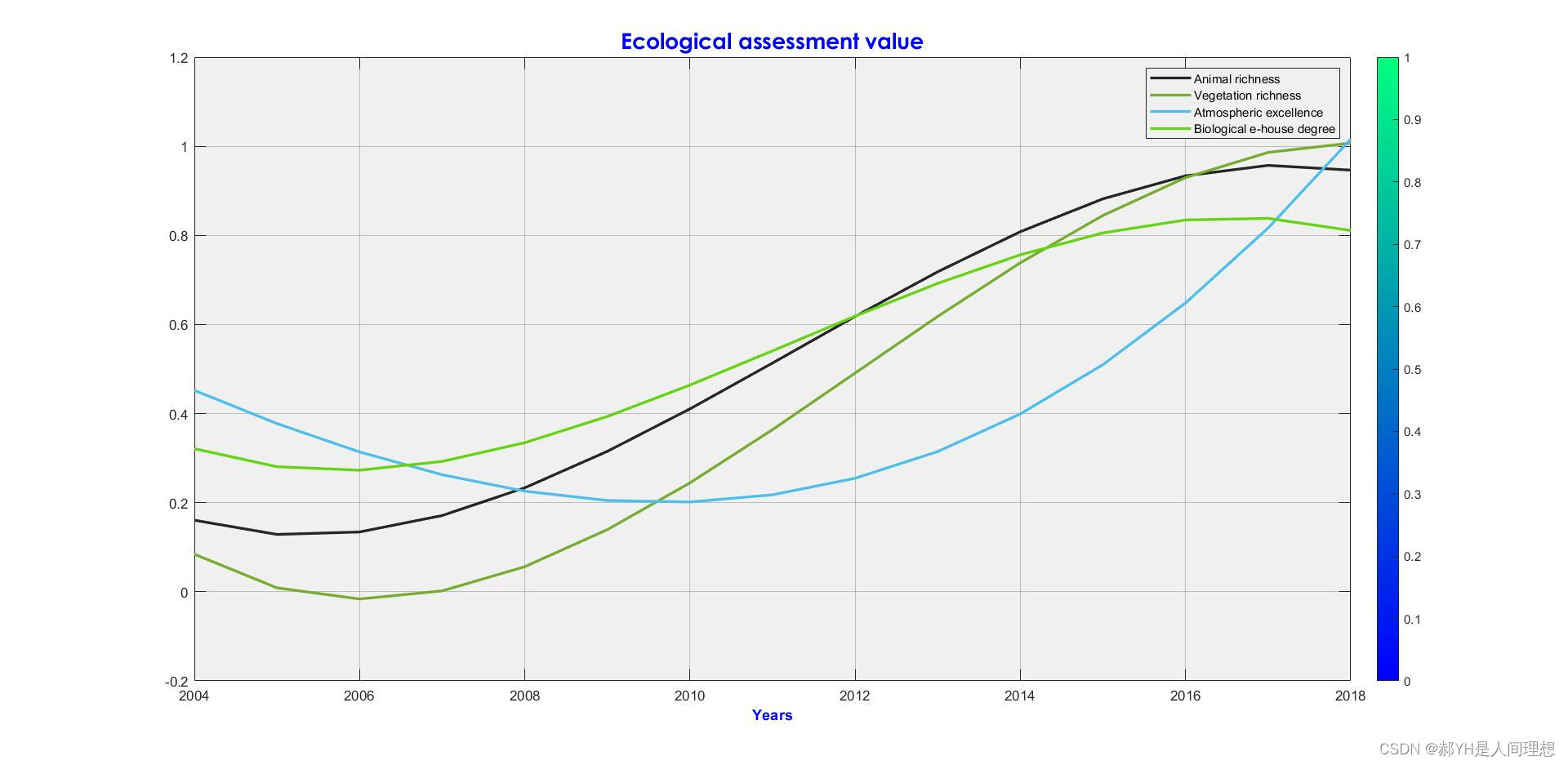
上图是2021年亚太数学建模中绘制的图片,根据有限数据量进行拟合得出具有函数性质的关系曲线
代码如下:
Time=[2004,2005,2006,2007,2008,2009,2010,2011,2012,2013,2014,2015,2016,2017,2018];
I1=[0.182948847,0.211434303,0,0.030892678,0.279638917,0.469635573,0.493306586,0.538642594,0.546666667,0.487288532,0.955466399,0.927382146,0.91334002,0.934603811,0.960280843];
I2=[0.022145329,0.034602076,0.033910035,0.028373702,0.044982699,0.195555556,0.277216455,0.342268358,0.349880815,0.364413687,0.919031142,0.990311419,1,0.948096886,0.948096886];
I3=[0.521140071,0.392131831,0.174670582,0.220460164,0.162032973,0.340698155,0.222348372,0.327533528,0.244249827,0.359156053,0.245644824,0.454187732,0.646707562,0.905064612,1];
I4=[0.36938131,0.374916005,0.117566088,0.148750878,0.372001753,0.388274379,0.51190998,0.705307237,0.695969953,0.706219511,0.591608401,0.759083664,0.819291342,0.822706134,0.874415287];
figure;
%% Create a canvas
a=polyfit(Time,I1,3);
plot(Time,I1,'.',Time,polyval(a,Time));%% Lock the current canvas,renders four function images on a single graph
hold on
b=polyfit(Time,I2,3);
plot(Time,I2,'.',Time,polyval(b,Time));
hold on
c=polyfit(Time,I3,3);
plot(Time,I3,'.',Time,polyval(c,Time));
hold on
d=polyfit(Time,I4,3);
plot(Time,I4,'.',Time,polyval(d,Time));
hold off
%% The command drawing part is finished, and the subsequent design is completed by graphic editing tools
%% FLG files will appear in the support material四.代码扩展
1.计算误差
y_hat = k*x+b; % y的拟合值
SSR = sum((y_hat-mean(y)).^2) % 回归平方和
SSE = sum((y_hat-y).^2) % 误差平方和
SST = sum((y-mean(y)).^2) % 总体平方和
SST-SSE-SSR % 5.6843e-14 = 5.6843*10^-14 matlab浮点数计算的一个误差
R_2 = SSR / SST2.产生随机数的一些操作:
% (1)randi : 产生均匀分布的随机整数(i = int)
%产生一个1至10之间的随机整数矩阵,大小为2x5;
s1 = randi(10,2,5)
%产生一个-5至5之间的随机整数矩阵,大小为1x10;
s2 = randi([-5,5],1,10)% (2) rand: 产生0至1之间均匀分布的随机数
%产生一个0至1之间的随机矩阵,大小为1x5;
s3 = rand(1,5)
%产生一个a至b之间的随机矩阵,大小为1x5; % a + (b-a) * rand(1,5); 如:a,b = 2,5
s4= 2 + (5-2) * rand(1,5)% (3)normrnd:产生正态分布的随机数
%产生一个均值为0,标准差(方差开根号)为2的正态分布的随机矩阵,大小为3x4;
s5 = normrnd(0,2,3,4)% (4)roundn—任意位置四舍五入
% 0个位 1十位 2百位 -1小数点后一位
a = 3.1415
roundn(a,-2) % ans = 3.1400
roundn(a,2) % ans = 0
a =31415
roundn(a,2) % ans = 31400
roundn(5.5,0) %6
roundn(5.5,1) %10写在最后:对于数学建模竞赛来说,拟合并不是一种很高端的计算手段——仅在需要明确的函数方程时才建议使用。对于预测类的问题,建议使用回归、灰色预测、BP神经网络等模型。
相关文章:

MATLAB实现函数拟合
目录 一.理论知识 1.拟合与插值的区别 2.几何意义 3.误差分析 二.操作实现 1.数据准备 2.使用cftool——拟合工具箱 三.函数拟合典例 四.代码扩展 一.理论知识 1.拟合与插值的区别 通俗的说,插值的本质是根据现有离散点的信息创建出更多的离散点…...
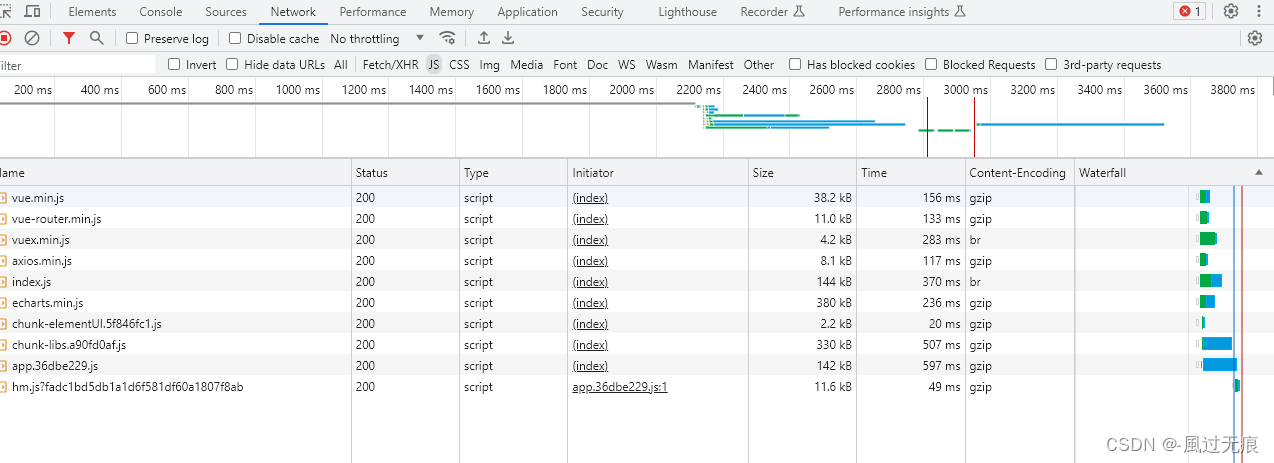
vue优化首屏加载时间优化-cdn引入第三方包
前言 为什么要进行首屏加载优化,因为随着我们静态资源和第三方包和代码增加,压缩之后包会越来越大 随着网络的影响,在我们第一输入url请求资源时候,网络阻塞,加载时间长,用户体验不好 仔细观察后就会发现…...

lv4 嵌入式开发-3 标准IO的读写
目录 1 标准I/O – 读写流 2 标准I/O – 按字符输入 3 标准I/O – 按字符输出 4 标准I/O – 思考和练习 5 标准I/O – 按行输入 6 标准I/O – 按行输出 7 标准I/O – 思考和练习 1 标准I/O – 读写流 流支持不同的读写方式: 读写一个字符:fgetc()/fputc()一…...

iOS UIDevice设备信息
识别设备和操作系统 //获得共享设备实例 open class var current: UIDevice { get }//识别设备的名称 open var name: String { get } // e.g. "My iPhone"//设备类型 open var model: String { get } // e.g. "iPhone", "iPod touch"//本地化设…...
编译安装)
SLAM ORB-SLAM2(2)编译安装
SLAM ORB-SLAM2(2)编译安装 1. 软件包依赖安装2. 依赖安装2.1. Eigen2.2. Pangolin2.3. OpenCV3. ORB-SLAM23.1. 源码下载3.2. 文件修改3.3. 扩大交换空间3.4. 编译1. 软件包依赖安装 以一个纯净的ubuntu20.04桌面版为例 1.首先设置软件源为清华源 2.安装必要依赖 sudo ap…...

第11节-PhotoShop基础课程-索套工具
文章目录 前言1.索套工具 选中后按Ctrl 可以移动2.加,减,交叉 shift alt 2.多边形索套工具 手动首尾相连 或者双击空地1.单击绘制直线选区2.双击结束绘制3.加,减,交叉4. delete可以删除节点 3.磁性索套工具1.沿着边缘自动吸附2.可…...
Json字符串内容比较-超实用版
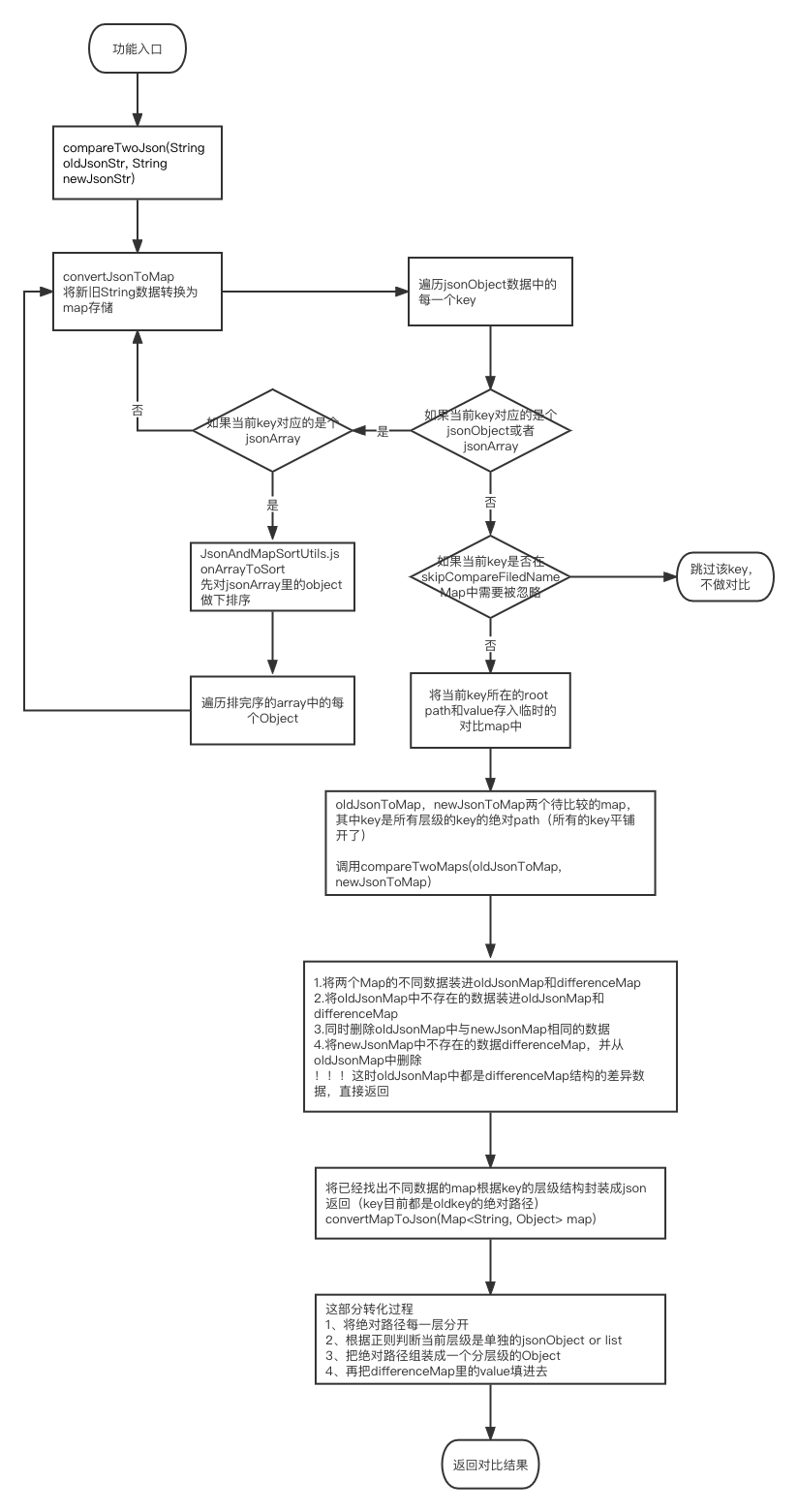
背景 之前有类似接口diff对比,数据对比的测试需求,涉及到json格式的数据对比,调研了几个大神们分享的代码,选了一个最符合自己需求的研究了下。 说明 这个对比方法,支持JsonObject和JsonArray类型的数据对比&#x…...

Redis系列之客户端Redisson
概述 官方推荐的客户端,支持Redis单实例、Redis哨兵、Redis Cluster、Redis master-slave等各种部署架构。 GitHub, 功能: 分布式锁 分布式锁 使用Redisson提供的分布式锁的一个最常见场景,应用部署为多个节点,然…...

centos 端口被占用的快速排查方式
问题笔记 centos 端口被占用的快速排查方式 centos 端口被占用的快速排查方式 这里说一个我刚刚遇到的问题,解决步骤用来记录,方便以后自己查询。 nginx配置完index.html测试文件,发现一直显示的404页面。 我跑到服务器上想重启一下nginx …...
Java“牵手”淘宝商品列表数据,关键词搜索淘宝商品数据接口,淘宝API申请指南
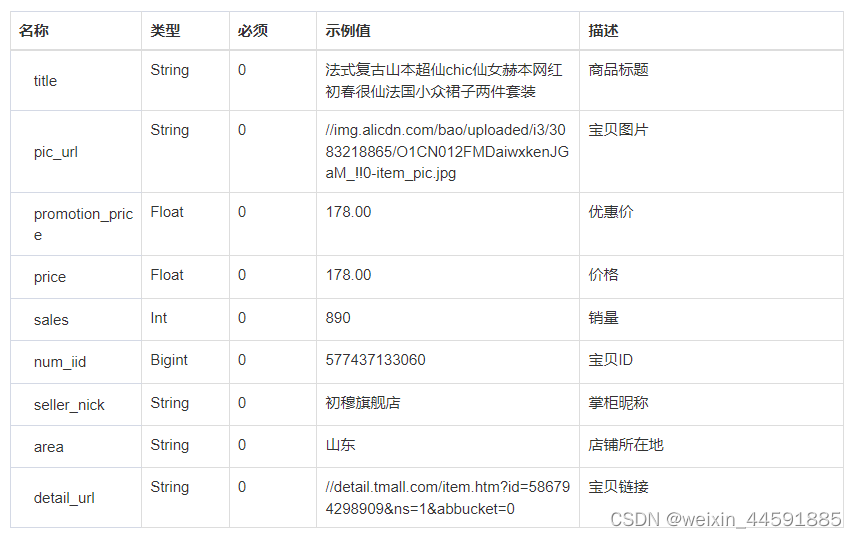
淘宝商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取淘宝商品列表和商品详情页面数据,您可以通过开放平台的接口或者直接访问淘宝商城的网页来获取商品详情信息。以下是两种常用方法的介绍&…...

OpenEuler/CentOS如何修改密码策略
密码策略文件: /etc/pam.d/system-auth 找到行: password requisite pam_pwquality.so try_first_pass local_users_only 为保证安全,可以将这一行注释掉,添加一行,最后结果如下: #password …...

# Spring MVC与RESTful API:如何设计高效的Web接口
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...
Scrum敏捷模式的优势点、实践经验及适用企业
Scrum敏捷模式是一种灵活、适应性强的开发方法,其核心理念是以短周期、高频率的方式进行项目开发,确保团队能够快速响应变化。 Scrum包含三个角色:产品负责人(Product Owner)、Scrum Master和开发团队(Tea…...

【C++杂货铺】探索stack和queue的底层实现
文章目录 一、stack的介绍和使用1.1 stack的介绍1.2 stack的使用1.2.1 最小栈1.2.2 栈的压入、弹出序列1.2.3 逆波兰表达式求值1.2.4 用栈实现队列 二、queue的介绍和使用2.1 queue的介绍2.2 queue的使用2.2.1 二叉树的层序遍历 三、模拟实现3.1 stack模拟实现3.2 queue模拟实现…...

“系统的UI”——SystemUI
SystemUI的实现 以StatusBar为例,来分析下Android系统具体是如何实现它们的。 相关代码分为两部分,即: Service部分 代码路径:frameworks/base/services/java/com/android/server。 应用部分 代码路径:frameworks…...
类和对象:构造函数,析构函数与拷贝构造函数
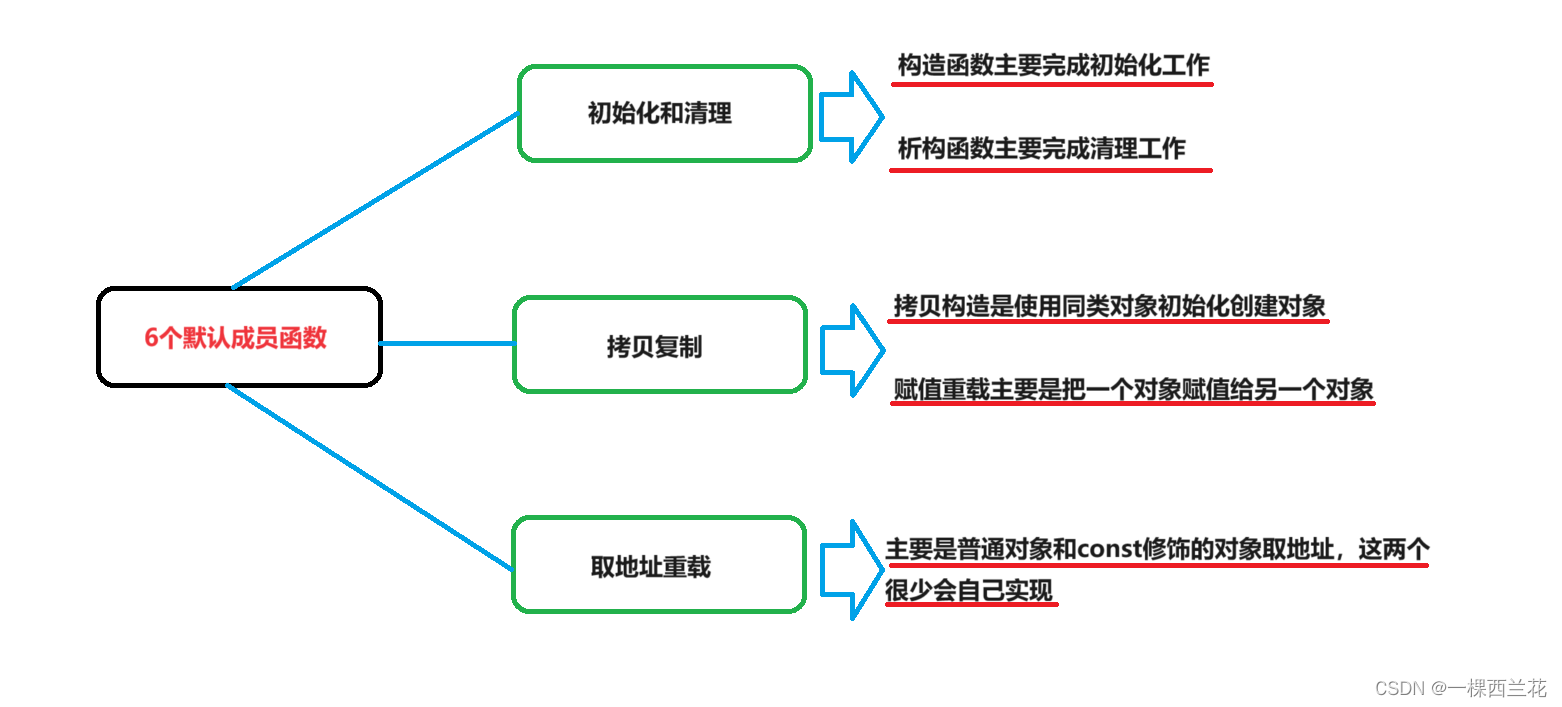
1.类的6个默认成员函数 如果一个类中什么成员都没有,简称为空类。 空类中真的什么都没有吗?并不是,任何类在什么都不写时,编译器会自动生成以下6个默认成员函数。 默认成员函数:用户没有显式实现,编译器…...

谈谈Java的特点和优点以及选择Java的原因
 如果面试官问你:请你说说Java的特点和优点,为什么要选择Java?你该怎么回答? 得分点 Java的特点 Java与C的区别 Java的优点标准回答 Java是一门非常纯粹的面向对象的编程语言,它吸收了C语言的各种优…...
面试)
消息队列(MQ)面试
目录 讲一讲MQ 面试官: 在你之前的项目中,你是否使用过消息队列(MQ)?能详细介绍一下你在项目中如何使用MQ吗? 在用户和用户之间的多对多聊天通信中如何使用,请具体来讲一下。 那你可以讲一下消息的确认…...

无涯教程-JavaScript - COUPNUM函数
描述 COUPNUM函数返回结算日和到期日之间应付的息票数量,四舍五入到最接近的整数。 语法 COUPNUM (settlement, maturity, frequency, [basis])争论 Argument描述Required/OptionalSettlement 证券的结算日期。 证券结算日期是指在发行日期之后将证券交易给买方的日期。 Re…...

上海控安携汽车网络安全新研产品出席AUTOSEMO“恒以致远,共创共赢”主题研讨会
8月31日,AUTOSEMO“恒以致远,共创共赢”主题研讨会在天津成功召开。本次大会由中国汽车工业协会软件分会中国汽车基础软件生态标委会(简称:AUTOSEMO)与天津市西青区人民政府联合主办。现场汇聚了100余位来自产学研政企…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...