【每日随笔】驾驭人性 ② ( 员工立场问题 | 立场转变 | 吴越同舟 | 老板如何与员工结成利益共同体 )
文章目录
- 一、员工立场问题
- 二、立场转变
- 三、吴越同舟
- 四、老板如何与员工结成利益共同体
一、员工立场问题
人的潜力是很大的 , 肩上抗 100 斤 水泥 和 肩上抗 100 斤黄金 , 能一样吗 , 扛着黄金绝对能扛回家 ;
员工 不愿意 与公司一条心是正常的 ,
员工 拿的是 死工资 , 公司赚了钱也不多分给 员工 , 公司倒闭了 , 员工直接跳槽换一家公司 ;
有些公司倒闭 , 并不是因为 员工能力差 , 而是 员工跟公司不是一条心 , 立场不坚定 , 对公司的死活抱着无所谓的态度 ;
员工的未来 与 公司的未来 没有任何关系 , 这明显就是公司的管理问题 ;
二、立场转变
如果 员工 立场 与 公司一致 , 员工 会 拼死力气 去为公司做事 ;
如果 员工 立场 与 公司不一致 , 认为公司倒闭 关我什么事 , 倒闭了重新找工作 ;
如果 员工 立场 与 其它公司一致 , 与本公司不一致 , 妥妥的商业间谍 ;
举个例子 :
潘金莲 与 武大郎 早期 生活的很好 , 他们是 利益共同体 ;
潘金莲 后来 与 西门庆 成为了 利益共同体 , 毒死了武大郎 ;
跟谁是 利益共同体 就跟谁是一条心 , 就是跟谁立场在一起 ;
三、吴越同舟
世界上 没有好人 , 也没有坏人 ;
- 跟自己立场一致 , 利益共同体的人 , 就是好人 ;
- 跟自己立场不同 , 损害自己利益的人 , 就是坏人 ;
只要利益改变了 , 立场也会相应改变 ;
吴越同舟 : 夫吴人与越人相恶也,当其同舟而济,遇风,其相救也,如左右手。
- 在春秋时期 , 吴国 和 越国经常打仗 , 两国的人也互相仇视 , 一见面就开打 ; 当两国人同时在船上时 , 遇到风浪 , 有沉默的危险 , 不管是吴国人还是越国人 , 都齐心协力 , 对抗风浪 , 顺利的安全靠岸 ;
- 开始 , 吴国人 和 越国人 都以自己国家的利益为立场 , 互相仇视 ;
- 然后 , 但是到了船上之后 , 两国人都的利益发生转换 , 都以活下来为自己的利益 , 双方利益一致 , 结成了利益共同体 , 立场一致 , 也就能同舟共济 ;
- 最后 , 到了岸上以后 , 继续开打 , 立场又变回原来的 对立立场 ;
四、老板如何与员工结成利益共同体
员工 与 公司 / 老板 , 二者是 赤裸裸的 利益关系 ,
在 利益分配 中 , 解决两件事 ,
- 员工 给谁 工作 ,
- 工作产出利润 , 怎么分 ,
让 员工 给老板干活 , 转为 让 员工 给 自己干活 ,
员工 干活后的利润分成 , 员工 拿大头 , 老板拿 小头 ,
这种利益关系是很稳定的 ;
你能让 客户 和 员工 在你身上占多少便宜 , 你的公司就有多大 ;
让 客户 和 员工 都觉得你傻 , 你就成功了 ;
给出多少利益参考 :
- 如果 员工跟着你干 , 利益回报 , 比他自己单干 , 利益要高 , 员工才有可能留在公司 , 你天天 PUA 员工 , 指着鼻子骂也不会走 , 为了钱挨点骂正常 ;
- 如果 员工跟着你干 , 利益回报比自己单干要少 , 比同行给的要少 , 员工此时是不稳定的 , 脾气可以大一些 , 老板一般指挥不动 ;
员工离职 , 一般两个原因 ,
- 钱给少了
- 受到委屈了
一般情况下 , 如果 钱给到位 , 受到委屈也没事 , 只有两个同时达成 , 人才会离职 ;
一个月给我六位数的工资 , 我连家都不回 ;
// 导入标准 io 流头文件 其中定义了 std 命名空间
#include <iostream>
// 导入 std 命名空间
using namespace std;int main() {// 控制台暂停system("pause");return 0;
}
相关文章:
)
【每日随笔】驾驭人性 ② ( 员工立场问题 | 立场转变 | 吴越同舟 | 老板如何与员工结成利益共同体 )
文章目录 一、员工立场问题二、立场转变三、吴越同舟四、老板如何与员工结成利益共同体 一、员工立场问题 人的潜力是很大的 , 肩上抗 100 斤 水泥 和 肩上抗 100 斤黄金 , 能一样吗 , 扛着黄金绝对能扛回家 ; 员工 不愿意 与公司一条心是正常的 , 员工 拿的是 死工资 , 公司赚…...
C++(QT)画图行车
通过鼠标在窗口上点击形成多个点的连线,绘制一辆汽车沿着绘制的连线轨迹前进。要求连线点数大于20.可以通过清除按钮清除已经绘制的连线,并可以重新绘制一条轨迹连线。当车辆行驶到轨迹终点时,自动停止。(汽车实在可用方块代替&am…...

Unity中Shader抓取屏幕并实现扭曲效果(优化)
文章目录 前言一、在之前顶点着色器的输入中,放弃了使用结构体传入,而是直接从应用程序阶段传入参数,这样写的话,对于程序来说,不方便扩张,所以需要对其进行修改实现1、定义结构体用于传入顶点坐标系2、因为…...
)
肖sir__设计测试用例方法之_(白盒测试)
白盒测试技术 一、定义: 白盒测试也叫透明盒测试,检查程序内部结构及路径一是否符合规格说明,二是否符合其代码规范。 因此,也叫结构测试或者逻辑驱动测试。 二、白盒测试常见方法: a、语句覆盖; b、判断覆…...
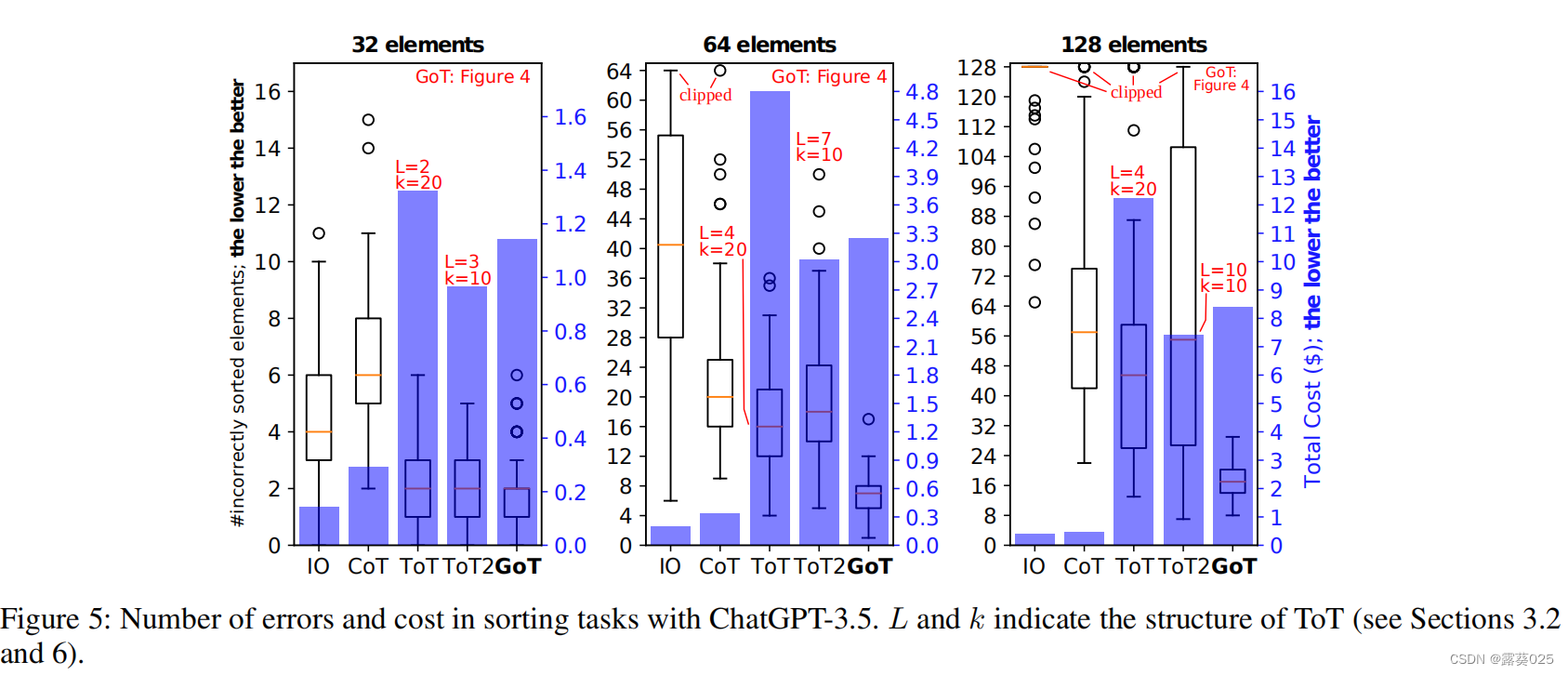
GoT:用大语言模型解决复杂的问题
GoT:用大语言模型解决复杂的问题 摘要介绍背景和符号表示语言模型和上下文学习Input-Output(IO)Chain of thought(CoT)Multiple CoTTree of thoughts(ToT) GoT框架推理过程思维变换聚合变换&…...

nginx服务和uwsgi服务如何设置开机自启动
上次学到了在云服务器下如何部署Django项目,用到了nginx服务和uwsgi服务,需要手工启动这2个服务的命令。 现在考虑如何设置开机自启动,为什么要这样考虑?因为服务器万一出问题,意外重启了,那我们部署的Dja…...

算法-分治算法
文章来源: https://blog.csdn.net/weixin_45630258/article/details/126425400 欢迎各位大佬指点、三连 一、分治 1、定义:分治,也就是分而治之。 它的一般步骤是: ① 将原问题分解成若干个规模较小的子问题(子问题…...

react 实现监听逻辑
需求: 在一个页面下有多个子tab在某些tab 下,或者父节点的数据更新的时候,其他子tab 或者父节点也要同步更新 进程: 正常情况下会把所有用到的数据都移动到父节点,修改行为也都放在父节点但如果这样的话父节点的数据…...

vue项目一个页面包含多个时间选择器的处理方案
描述:vue项目中如果在一个页面使用多个时间选择器组件时,不同的时间选择器需要分别分开工作 解决方案一 原本是想直接每一个时间选择器都安排一套相对独立的维生系统,但是到后面发现繁琐至极,而且报错,果断放弃&#…...
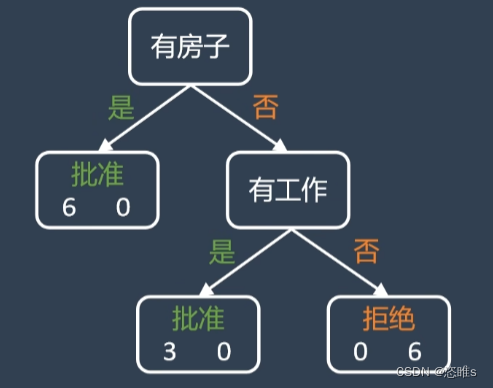
机器学习入门教学——决策树
1、简介 决策树算法是一种归纳分类算法,它通过对训练集的学习,挖掘出有用的规则,用于对新数据进行预测。决策树算法属于监督学习方法。决策树归纳的基本算法是贪心算法,自顶向下来构建决策树。 贪心算法:在每一步选择…...

文献阅读:Chain-of-Thought Prompting Elicits Reasoning in Large Language Models
文献阅读:Chain-of-Thought Prompting Elicits Reasoning in Large Language Models 1. 文章简介2. 具体方法3. 实验结果 1. 数学推理 1. 实验设计2. 实验结果3. 消解实验4. 鲁棒性考察 2. 常识推理 1. 实验设计2. 实验结果 3. 符号推理 1. 实验设计2. 实验结果 4.…...

从零开发一款ChatGPT VSCode插件
本文作者是360奇舞团开发工程师 引言 OpenAI发布了ChatGPT,就像是给平静许久的互联网湖面上扔了一颗重磅炸弹,刹那间所有人都在追捧学习它。究其原因,它其实是一款真正意义上的人工智能对话机器人。它使用了深度学习技术,通过大…...

go基础09-Go语言的字符串类型
字符串类型是现代编程语言中最常使用的数据类型之一。在Go语言的先祖之一C语言当中,字符串类型并没有被显式定义,而是以字符串字面值常量或以’\0’结尾的字符类型(char)数组来呈现的: #define GOAUTHERS "Rober…...

【C++模拟实现】手撕AVL树
【C模拟实现】手撕AVL树 目录 【C模拟实现】手撕AVL树AVL树的介绍(百度百科)AVL树insert函数的实现代码验证是否为AVL树AVL树模拟实现的要点易忘点AVL树的旋转思路 作者:爱写代码的刚子 时间:2023.9.10 前言:本篇博客将…...

如何重置 docker中的mariadb的root
停止 Mariadb 容器:运行以下命令停止正在运行的 Mariadb 容器: docker stop <container_name>将 <container_name> 替换为你的 Mariadb 容器的名称或容器ID。 删除 Mariadb 容器:运行以下命令删除已停止的 Mariadb 容器&#x…...

设计模式系列-原型模式
一、上篇回顾 上篇创建者模式中,我们主要讲述了创建者的几类实现方案,和创建者模式的应用的场景和特点,创建者模式适合创建复杂的对象,并且这些对象的每 个组成部分的详细创建步骤可以是动态的变化的,但是每个对象的组…...

家用电脑可以用做服务器吗
家用电脑的结构与服务器的结构是相同的,家用电脑是可以用来搭建服务器使用。但使用家用电脑做服务器在稳定性会比服务器差很多 1.家用电脑没有公网IP,网络运营商分配的IP重启路由之后是会变化,不固定。服务器运行是需要有固定IP让人连接访问。…...

CRM软件管理系统的基本功能
CRM管理系统是企业运营的重要工具,它可以帮助企业管理客户关系,提升销售效率,大幅提高客户转化率,实现业绩增长。那么,CRM管理系统一般包含哪些功能呢?下面我们就来说说。 1、销售自动化 销售自动化顾名思…...

手机喊话应用实现思路
手机要是动一下,就喊话“摇摇零线,摇摇零线”,是不是比较酷, 这里实现一下手机翻转一下,播放声音的效果, 通过sensor识别到手机的运动状况,然后播放音频, public class MainActivi…...

【ARM CoreLink 系列 3 -- CCI-550 控制器介绍 】
文章目录 CCI FamilyCCI-550 简介CCI-550 功能CCI-550 Interfaces Snoop filter 使用背景CCI-550 Snoop filter 上篇文章:ARM CoreLink 系列 2 – CCI-400 控制器简介 CCI Family CCI-550 简介 Arm CoreLink CCI-550 Cache Coherent Interconnect 扩展了 CoreLink…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
