【蓝桥杯集训8】哈希表专题(3 / 3)
目录
手写哈希表
1、开放寻址法
2、拉链法
字符串前缀哈希表法
2058. 笨拙的手指 - 哈希表 + 秦九韶算法(进制转换)+ 枚举
秦九韶算法——将x进制数转化为十进制数
手写哈希表
活动 - AcWing
1、开放寻址法
设 h(x)=k,也就是 x 的哈希值为 k
如果在 hash[k]的位置已经有元素,持续往后遍历直到找到 >x(询问)或为空(插入)为止
注意开放寻址法一般会把数组开到数据范围的 2−3 倍,能提高效率
import java.util.*;class Main
{static int N=200003,nul=0x3f3f3f3f; //质数static int[] h=new int[N];public static int find(int x){int k=(x%N+N)%N;while(h[k]!=nul&&h[k]!=x) //如果该坑位不为空且该坑位不为x(如果x已经存过就不存了){k++;if(k==N) k=0;}return k; //如果找到x,则返回x所在的位置//如果没有找到x,则返回x应该存放的位置}public static void main(String[] args){Scanner sc=new Scanner(System.in);int n=sc.nextInt();Arrays.fill(h,nul);while(n-->0){String s=sc.next();int x=sc.nextInt();int k=find(x);if(s.equals("I")) h[k]=x;else if(s.equals("Q")){if(h[k]!=nul) System.out.println("Yes");else System.out.println("No");}}}
}
2、拉链法
设 h(11)=3,h(23)=3 ,这就是一种冲突
我们可以设一个数组h,也就是哈希的结果
对于每一个结果k,建立一个链表
把映射为 k 的所有数 x 都放在 h[k] 这个链表里
import java.util.*;class Main
{static int N=100003; //质数static int[] h=new int[N],e=new int[N],ne=new int[N];static int idx;public static void insert(int x){int k=(x%N+N)%N; //+N%N是为了让负数变成正数e[idx]=x;ne[idx]=h[k];h[k]=idx++;}public static boolean find(int x){int k=(x%N+N)%N;for(int i=h[k];i!=-1;i=ne[i])if(e[i]==x) return true;return false;}public static void main(String[] args){Scanner sc=new Scanner(System.in);int n=sc.nextInt();Arrays.fill(h,-1);while(n-->0){String s=sc.next();int x=sc.nextInt();if(s.equals("I")) insert(x);else if(s.equals("Q")){if(find(x)) System.out.println("Yes");else System.out.println("No");}}}
}
字符串前缀哈希表法
把字符串变成一个p进制数字(哈希值),实现不同的字符串映射到不同的数字
对形如
的字符串,采用字符的ascii 码乘上 P 的次方来计算哈希值
映射公式
注意:
- 任意字符不可以映射成0,否则会出现不同的字符串都映射成0的情况,比如A,AA,AAA皆为0
- 通过巧妙设置P (131 或 13331) , Q (
)的值,一般可以理解为不产生冲突
比较不同区间的子串是否相同,就转化为对应的哈希值是否相同
求一个字符串的哈希值就相当于求前缀和,求一个字符串的子串哈希值就相当于求部分和
字符串前缀和公式:
h[i] = h[i-1]*P + s[i];区间和公式:
区间和公式的理解: ABCDE 与 ABC 的前三个字符值是一样,只差两位,
乘上把 ABC 变为 ABC00,再用 ABCDE - ABC00 得到 DE 的哈希值
活动 - AcWing
题目:
import java.util.*;class Main
{static int N=100010;static long[] h=new long[N],p=new long[N];static int P=131;public static void main(String[] args){Scanner sc=new Scanner(System.in);int n=sc.nextInt(),m=sc.nextInt();String s="/"+sc.next();//下标从1开始p[0]=1;for(int i=1;i<=n;i++){p[i]=p[i-1]*P;h[i]=h[i-1]*P+s.charAt(i);}while(m-->0){int l1=sc.nextInt(),r1=sc.nextInt();int l2=sc.nextInt(),r2=sc.nextInt();long h1=h[r1]-h[l1-1]*p[r1-l1+1];long h2=h[r2]-h[l2-1]*p[r2-l2+1];System.out.println(h1==h2?"Yes":"No");}}
}2058. 笨拙的手指 - 哈希表 + 秦九韶算法(进制转换)+ 枚举
2058. 笨拙的手指 - AcWing题库
题目:
第一行给你一个N的二进制表示,其中有一位是错误的
第二行给你一个N的三进制表示,其中有一位是错误的
输出N的正确十进制值(题目保证一定有唯一解)
思路:
枚举二进制数a的所有换1位的情况,转化为十进制值存入哈希表
枚举三进制数b的所有换1位情况,转化为十进制后在哈希表中查询是否存在
因为题目保证一定有唯一解,所以两者交集即为答案
因此如果查询到,则输出
秦九韶算法——将x进制数转化为十进制数
public static int get(String s,int x) {int res=0;for(int i=0;i<s.length();i++){char t=s.charAt(i);res=res*x + t-'0';}return res; }
import java.util.*;class Main
{static int N=100010;public static int get(char[] s,int x)//将x进制数s转化为十进制数{//秦九韶算法int res=0;for(int i=0;i<s.length;i++){res=res*x+s[i]-'0';}return res;}public static void main(String[] args){Scanner sc=new Scanner(System.in);char[] a=sc.next().toCharArray();char[] b=sc.next().toCharArray();Set<Integer> st=new HashSet<>();for(int i=0;i<a.length;i++){a[i]^=1;st.add(get(a,2));a[i]^=1;}for(int i=0;i<b.length;i++){char t=b[i];for(int j=0;j<3;j++) //将这一位换成除了本身的其他数if(t-'0'!=j){b[i]=(char)(j+'0');int tp=get(b,3);if(st.contains(tp)){System.out.print(tp);return;}}b[i]=t; //换完该位要恢复现场 继续换下一位}}
}相关文章:

【蓝桥杯集训8】哈希表专题(3 / 3)
目录 手写哈希表 1、开放寻址法 2、拉链法 字符串前缀哈希表法 2058. 笨拙的手指 - 哈希表 秦九韶算法(进制转换) 枚举 秦九韶算法——将x进制数转化为十进制数 手写哈希表 活动 - AcWing 1、开放寻址法 设 h(x)k,也就是 x 的哈希值…...

Java Scanner 类,超详细整理,适合新手入门
目录 一、什么是 Java Scanner 类? 二、引用数据类型 1、引用数据类型的定义 三、Scanner 类有哪些常用方法? hasNext()用法 四、next() 与 nextLine() 区别 next(): nextLine(): 五、使用 next 方法 五、使用 nextLine方法 一、什…...

干货 | 中小企业选型 Elasticsearch 避坑指南
1、线上常见问题在我线下对接企业或线上交流的时候,经常会遇到各种业务场景不同的问题。比如,常见问题归类如下:常见问题1:ES 适合场景及架构选型问题。公司的核心业务是做企业员工健康管理,数据来自电子化后的员工体检…...
全局组件和局部组件
全局组件第一种定义方法:A、创建自己的组件:Loading.vueB、在main.js文件中引入组件并注册import Vue from vue import App from ./App.vue import * as filters from ./filterimport quanjuzujian from ./components/quanjuzujian.vueVue.component(qua…...
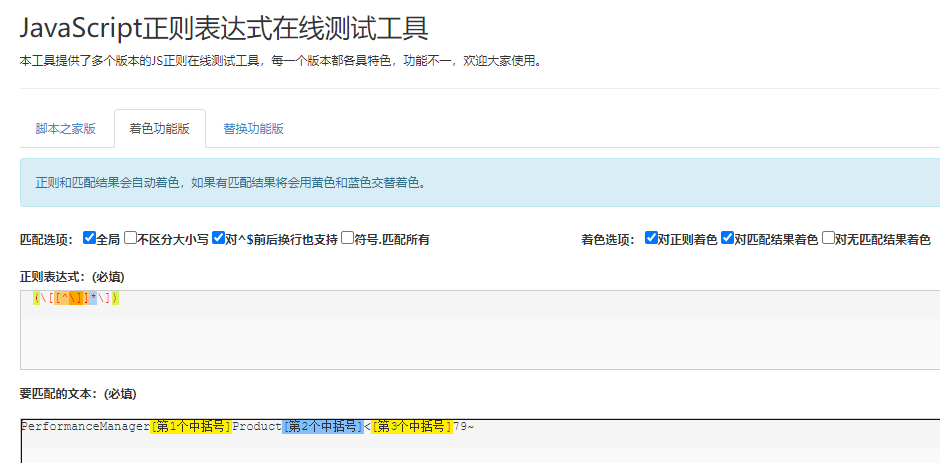
提取括号中的内容
正则能解决不嵌套的括号内容提取问题遇到一个问题,就是需要提取字符串中每一个中括号里的内容,在网上搜了一下,发现用正则表达式(\[[^\]]*\])可以提取中括号中的内容,以下面文本为匹配对象:PerformanceManager[第1个中…...

数据结构-算法的空间复杂度(1.2)
目录 1.空间复杂度 1.1 例子 1.2 空间的特殊性质 写在最后: 1.空间复杂度 空间复杂度也是一个数学表达式, 是对一个算法在运行过程中临时占用存储空间大小的量度。 他也是用大O渐进表示法。 1.1 例子 例1: 冒泡排序: v…...
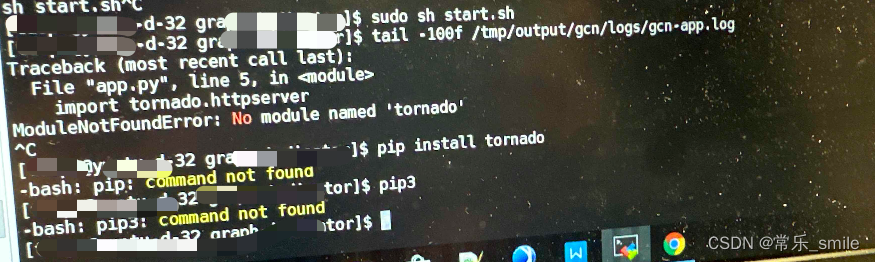
【总结】python3启动web服务引发的一系列问题
背景 在某行的实施项目,需要使用python3环境运行某些py脚本。 由于行内交付的机器已自带python3 ,没有采取自行安装python3,但是运行python脚本时报没有tornado module。 错误信息 ModuleNotFoundError:No module named ‘torn…...
Linux:基于libevent读写管道代码,改进一下上一篇变成可以接收键盘输入
对上一篇进行改进,变成可以接收键盘输入,然后写入管道: 读端代码: #include <stdlib.h> #include <stdio.h> #include <unistd.h> #include <sys/types.h> #include <sys/stat.h> #include <s…...
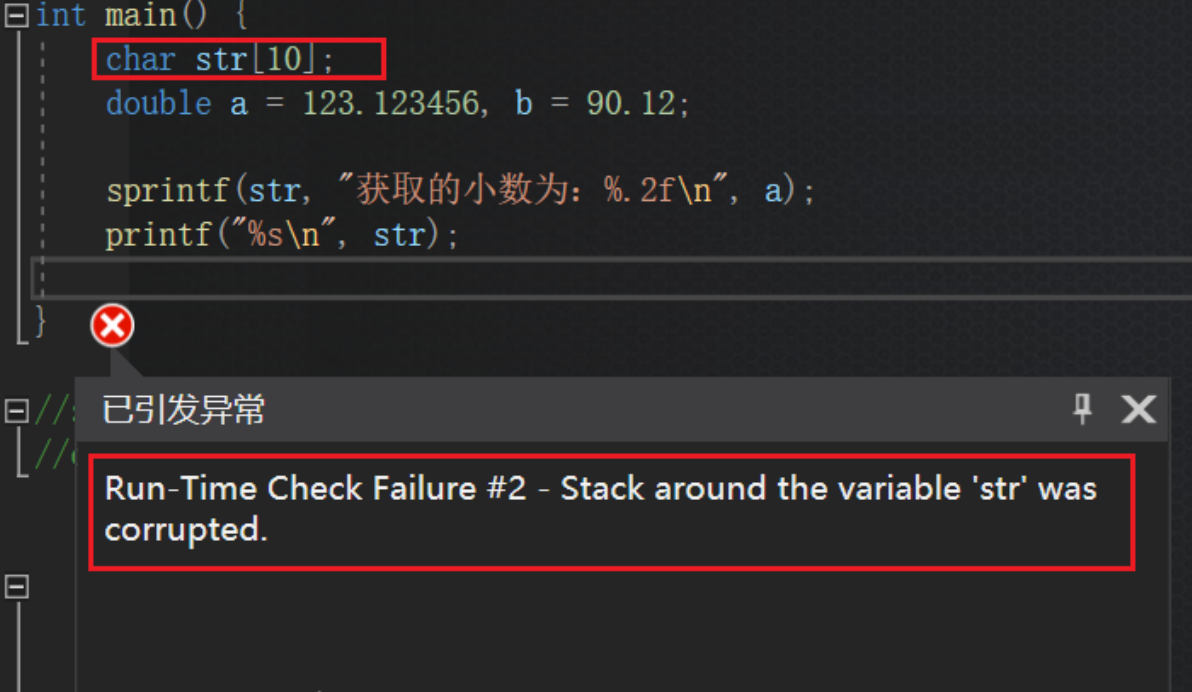
C语言格式化输出总结:%d,%c,%s,%f, %lf,%m.nd,%m.nf,%m.ns 以及sprintf函数
凡事发生必将有益于我,高手,从来都不仅仅是具备某种思维的人,而是那些具备良好学习习惯的人,成为高手,无他,手熟尔!加油在最近的学习之中,对于格式化输出这个知识点,这里…...
Nginx之反向代理、负载均衡、动静分离。
Nginx之反向代理、负载均衡、动静分离。 1、Nginx是啥? 轻量级Web服务器、反向代理服务器、电子邮件(IMAP/POP3)代理服务器 在 BSD-like 协议下发行、占内存少、并发高(同时处理请求能力)。 2、安装 官网…...
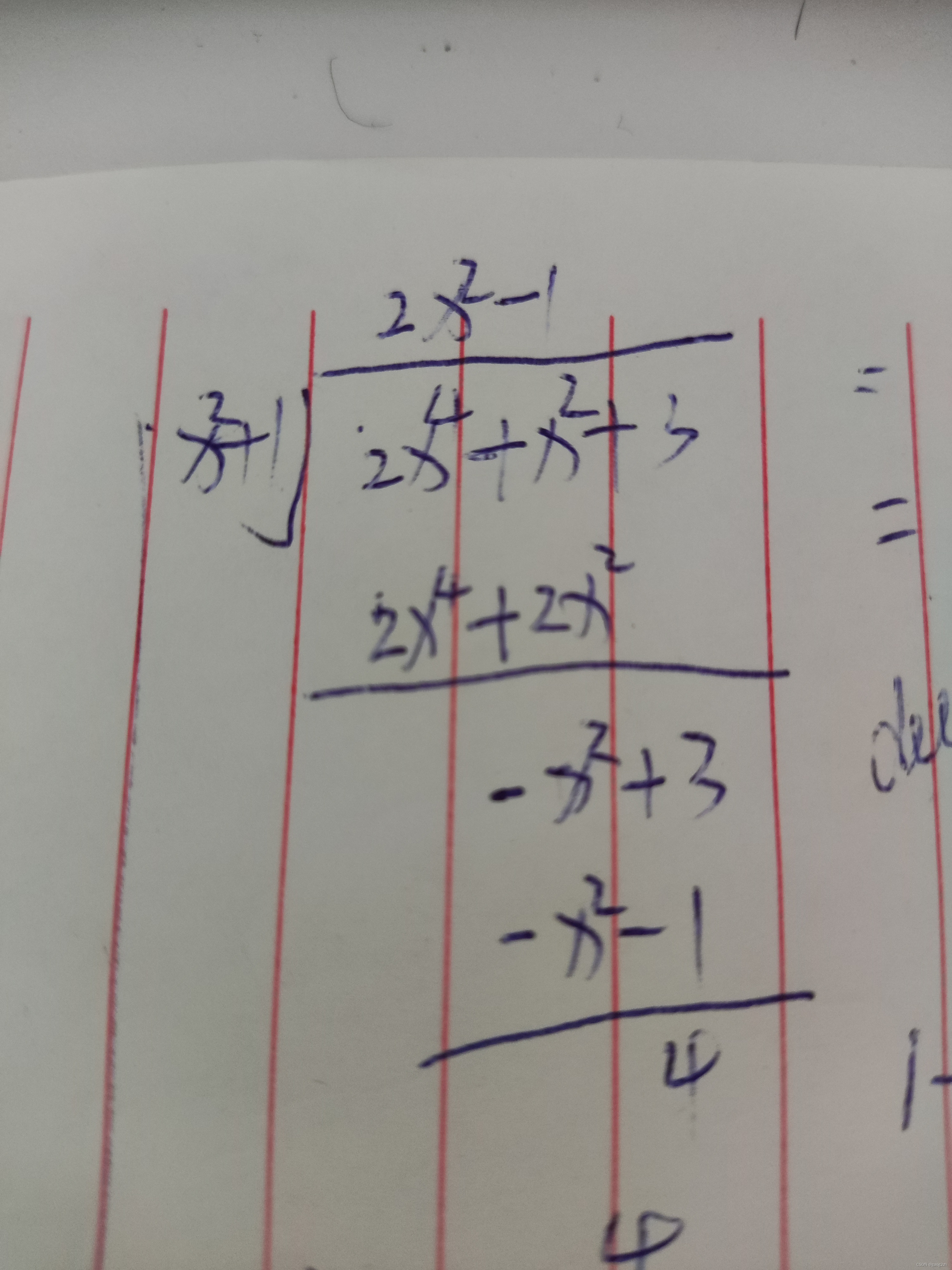
0401不定积分的概念和性质-不定积分
文章目录1 原函数与不定积分的概念1.1 原函数1.2 原函数存在定理1.3 不定积分2 不定积分的性质3 基本积分表4 例题后记1 原函数与不定积分的概念 1.1 原函数 定义1 如果在区间I上,可导函数F(x)的导航为f(x),即对任一x∈Ix\in Ix∈I,都有 F′…...

数组中的各种迭代API方法手写
js的数组上有很多实用的方法,不论是在遍历数组上,还是在操作数组内元素上,它有许多不同的遍历数组的方法,同时它还有着可以直接操作数组中间元素的方法。 接下来,我来带大家手写数组里的 遍历方法 。 Array.forEach(…...
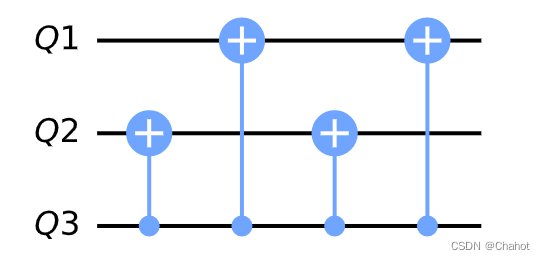
详解量子计算:相位反冲与相位反转
前言 本文需要对量子计算有一定的了解。需要的请翻阅我的量子专栏,这里不再涉及基础知识的科普。 量子相位反冲是什么? 相位反转(phase kickback)是量子计算中的一种现象,通常在量子算法中使用,例如量子…...
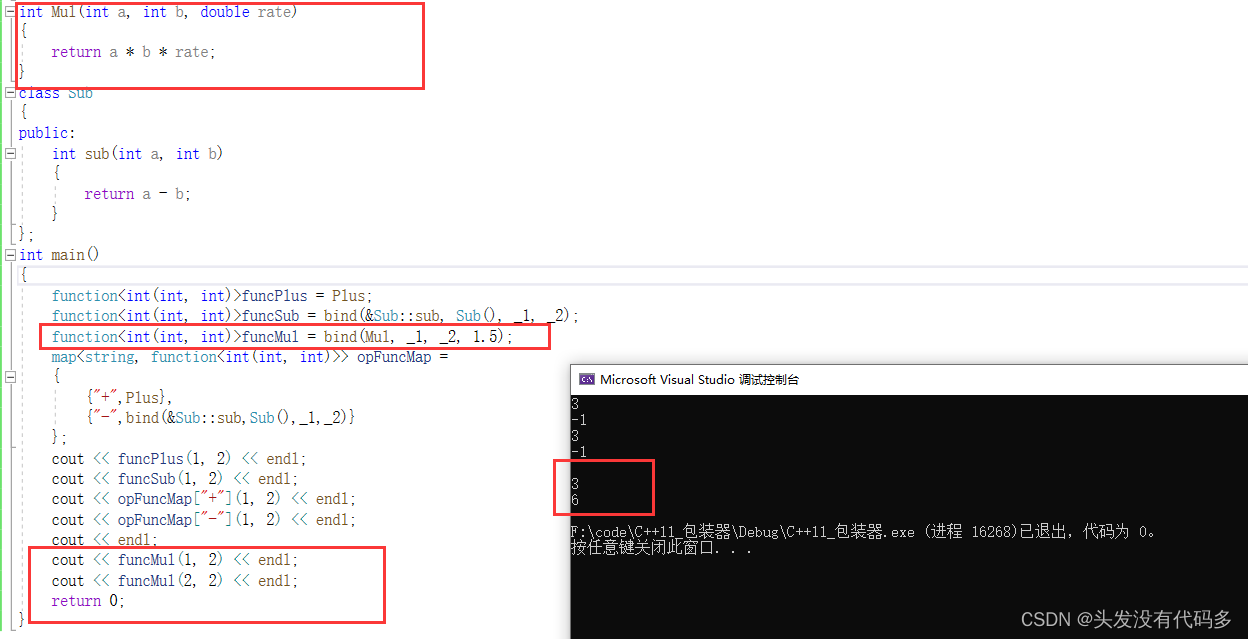
C++——C++11第三篇
目录 包装器 function包装器 bind 包装器 function包装器 function包装器 也叫作适配器。C中的function本质是一个类模板,也是一个包装器。 上面的程序验证,我们会发现useF函数模板实例化了三份。 包装器可以很好的解决上面的问题 ,让它只实…...

180 2 22222
选择题(共180题,合计180.0分) 1. 在项目开工会议期间,项目发起人告诉产品负责人和团队项目章程即将完成。然而,由于存在在紧迫的期限内满足政府监管要求的压力,发起人希望立即开始工作。产品负责人下一步应该做什么? A 告诉发起人…...

成人高考初中毕业能报名吗 需要什么条件
初中学历的人员不能直接报名成人高考,考生需要有普通高中,职业高中,中专毕业证等高中同等学力就可以进行报名,在报名期间登陆所在省的教育考试院的成人高考报名入口进行报考。成人高考报名条件是什么1、遵守宪法和法律。2、国家承…...

ChatGPT初体验
ChatGPT初体验 前言 嘿嘿,最近啊AI ChatGPT刷新各大网站,对于我们国人而将很不友好,真的太不友好了。我呢在去年open AI发布的时候就有所关注,那个时候还没有像现在这样火热。谁知道短短几个月便传遍大街小巷。 一、什么是chatG…...

ChatGPT概念狂飙!究竟魅力何在?
原文:http://www.btcwbo.com/6988.html 近期,ChatGPT引领的人工智能概念在资本市场一路狂飙,AIGC题材持续发酵。截至2月7日,Wind ChatGPT指数今年以来累计上涨超50%,汉王科技、海天瑞声、云从科技等概念股股价已经翻倍…...
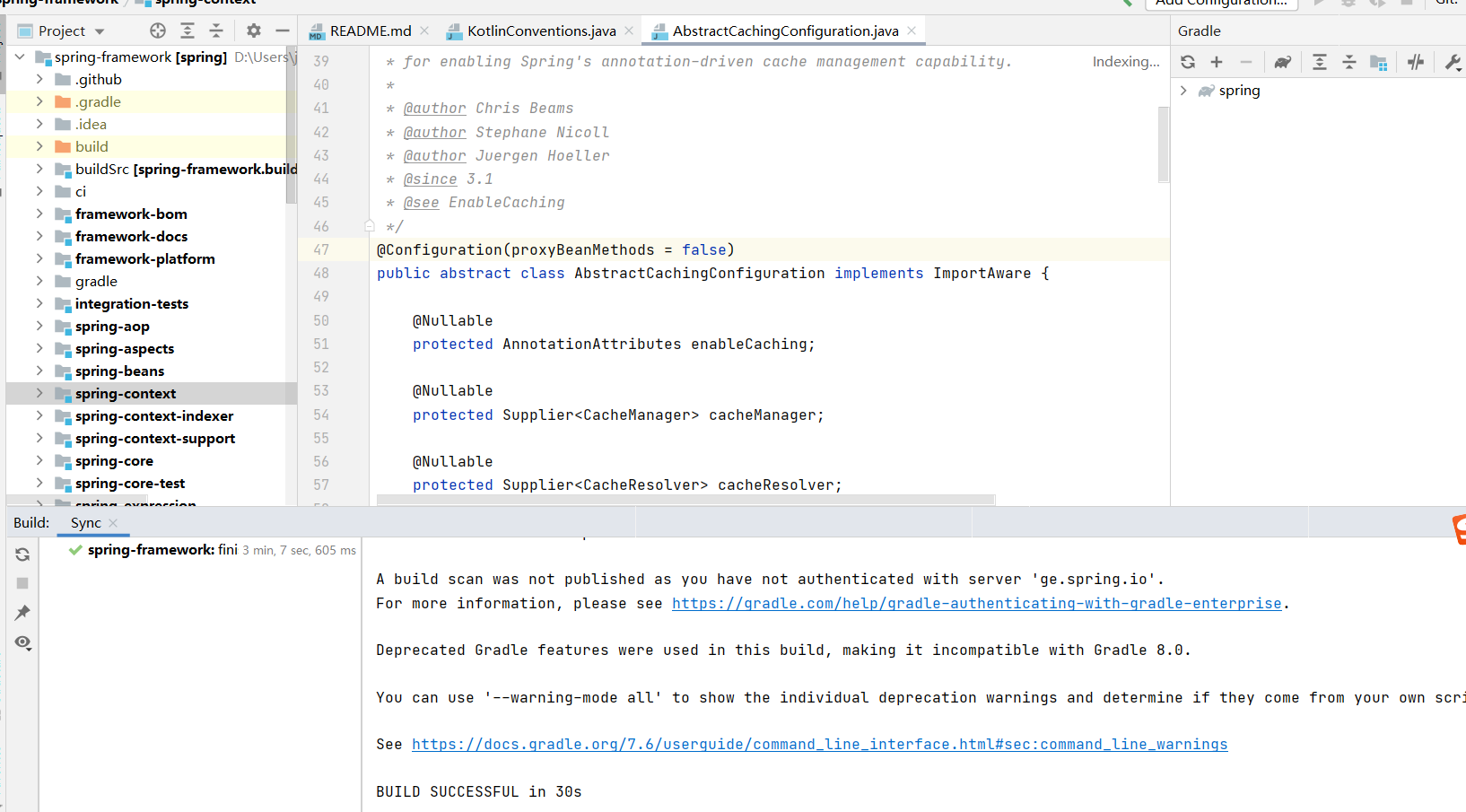
如何下载阅读Spring源码-全过程详解
这篇文章记录了下载spring源码和在IDEA中打开运行的全过程,并且记录了过程中遇到的问题和解决方案,适合需要学习spring源码的同学阅读。 1.spring源码下载地址 通过Git下载spring-framework项目源码: git clone https://github.com/spring…...
学了两个月的Java,最后自己什么也不会,该怎么办?
学着学着你会发现每天的知识都在更新,也都在遗忘,可能就放弃了。但是只要自己肯练,肯敲代码,学过的知识是很容易就被捡起来的。等你学透了用不了一年也可以学好 Java的运行原理:Java是一门编译解释型语言,…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

