详解量子计算:相位反冲与相位反转
前言
本文需要对量子计算有一定的了解。需要的请翻阅我的量子专栏,这里不再涉及基础知识的科普。
量子相位反冲是什么?
相位反转(phase kickback)是量子计算中的一种现象,通常在量子算法中使用,例如量子相位估计算法。相位反冲可以用于将某些运算转化为在控制比特上的操作,从而实现更高效的量子算法。
相位反冲的主要思想是将一个控制比特和一个目标比特连接在一起,然后将目标比特进行某种操作,这个操作的相位会反冲到控制比特上,使得控制比特的状态发生改变。这样,我们可以通过测量控制比特的状态来获取目标比特上的信息。
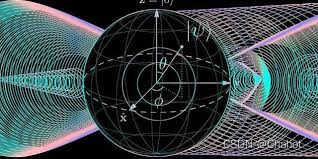
例如,在量子相位估计算法中,我们想要估计一个相位角θ,我们可以构造一个相应的幺正运算U,将一个有用的状态|ψ⟩作为目标比特,将一个初始状态|0⟩作为控制比特,并将它们连接在一起。然后,对控制比特应用Hadamard门,使得它处于|+⟩状态,接着对U进行一个特定的操作,使得它的相位角为2kθ,其中k是控制比特的状态,最后再对控制比特进行测量,从而可以得到θ的估计。在这个过程中,相位反冲起到了关键作用,将目标比特的相位信息传递给了控制比特。
理解相位反冲
假设我们有一个叠加态 ∣+⟩=12(∣0⟩+∣1⟩)|+\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)∣+⟩=21(∣0⟩+∣1⟩),和一个初始状态为 ∣0⟩|0\rangle∣0⟩ 的控制比特和目标比特。我们可以将它们放在一个线路中,并将控制比特上的Hadamard门作用在上面,将叠加态 ∣+⟩|+\rangle∣+⟩ 与控制比特进行叠加,然后再应用CNOT门,将控制比特作为控制量子比特,目标比特作为目标量子比特。 这个操作的结果是
12(∣0⟩+∣1⟩)⊗∣0⟩→Hadamard on control bit12(∣0⟩+∣1⟩)(∣0⟩−∣1⟩)→CNOT12(∣00⟩−∣01⟩+∣10⟩−∣11⟩)\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) \otimes |0\rangle \xrightarrow{\text{Hadamard on control bit}} \frac{1}{2}(|0\rangle + |1\rangle)(|0\rangle - |1\rangle) \xrightarrow{\text{CNOT}} \frac{1}{2}(|00\rangle - |01\rangle + |10\rangle - |11\rangle)21(∣0⟩+∣1⟩)⊗∣0⟩Hadamard on control bit21(∣0⟩+∣1⟩)(∣0⟩−∣1⟩)CNOT21(∣00⟩−∣01⟩+∣10⟩−∣11⟩)
控制比特的状态(第一个量子比特)已经传递到了目标比特的相位上。这就是相位反冲技术的一个例子。为了更好的理解他,对下面的一些概念进行普及:
正交归一化叠加态
12(∣0⟩+∣1⟩)⊗∣0⟩→12(∣00⟩+∣11⟩),12(∣0⟩+∣1⟩)⊗∣1⟩→12(∣01⟩+∣10⟩)\begin{aligned} \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\otimes|0\rangle &\rightarrow \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle), \ \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\otimes|1\rangle &\rightarrow \frac{1}{\sqrt{2}}(|01\rangle + |10\rangle) \end{aligned}21(∣0⟩+∣1⟩)⊗∣0⟩→21(∣00⟩+∣11⟩), 21(∣0⟩+∣1⟩)⊗∣1⟩→21(∣01⟩+∣10⟩)
这个量子态可以写成:
12(∣0⟩⊗∣0⟩+∣1⟩⊗∣1⟩)\frac{1}{\sqrt{2}}(|0\rangle\otimes|0\rangle + |1\rangle\otimes|1\rangle)21(∣0⟩⊗∣0⟩+∣1⟩⊗∣1⟩)
其中∣0⟩⊗∣0⟩|0\rangle\otimes|0\rangle∣0⟩⊗∣0⟩和∣1⟩⊗∣1⟩|1\rangle\otimes|1\rangle∣1⟩⊗∣1⟩是基矢量,也就是正交的。因此,这个量子态是一个正交归一化叠加态。
假设有一个初始态 ∣ψ⟩=∣0⟩|\psi\rangle = |0\rangle∣ψ⟩=∣0⟩,然后应用了一个 Hadamard 门,得到的叠加态为:∣ψ′⟩=H∣ψ⟩=12(∣0⟩+∣1⟩)|\psi'\rangle=H|\psi\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)∣ψ′⟩=H∣ψ⟩=21(∣0⟩+∣1⟩)
接着,将 ∣ψ′⟩|\psi'\rangle∣ψ′⟩ 作为控制态,和一个目标态 ∣ψ′′⟩=∣0⟩|\psi''\rangle = |0\rangle∣ψ′′⟩=∣0⟩ 经过 CNOT 门,得到的最终态为:∣ψfinal⟩=12(∣00⟩+∣11⟩)|\psi_{final}\rangle = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)∣ψfinal⟩=21(∣00⟩+∣11⟩)
此时,第一个量子比特处于正交归一化叠加态。而这个过程中就涉及了相位反演。
在量子力学中,一个系统可以被表示为其基态的叠加,每个基态都是一个量子态。如果基态是正交的且归一化,那么它们可以构成一个正交归一化基。一个系统也可以被表示为不同的基的线性组合,这些基构成正交归一化叠加态。这些叠加态不仅是描述量子态的方便工具,而且在许多实际应用中也具有重要作用,比如在量子计算和量子通信中。
下面是系统的概念:
正交归一化叠加态: 在量子力学中,一个量子态是指一个量子系统所处的状态。量子态可以用一个或多个复数表示,其中每个复数都对应于系统的一个可能状态。当涉及到多个态时,为了避免出现混乱,需要对这些态进行归一化和正交化。
归一化是指将一个向量除以其长度,以使其长度等于1。在量子力学中,归一化态是一个长度为1的量子态,它是由量子态中的每个系数除以归一化系数而得到的。归一化态在量子力学中非常重要,因为在某些情况下,只有归一化的态才能表示物理上可观测的状态。为了理解这个概念,下面我们来看一些例子:
12∣000⟩+32∣111⟩\frac{1}{2}|000\rangle + \frac{\sqrt{3}}{2}|111\rangle21∣000⟩+23∣111⟩:这是一个三量子比特的量子态。它的归一化系数为14+34=1\sqrt{\frac{1}{4} + \frac{3}{4}} = 141+43=1。
13∣000⟩+23∣111⟩\frac{1}{\sqrt{3}}|000\rangle + \sqrt{\frac{2}{3}}|111\rangle31∣000⟩+32∣111⟩:这是一个三量子比特的量子态。它的归一化系数为13+23=1\sqrt{\frac{1}{3} + \frac{2}{3}} = 131+32=1。
正交是指两个向量之间的内积为0,或者说两个向量之间的夹角为90度。在量子力学中,正交态是两个不同的量子态之间的内积为0的态。这意味着这些态可以互相区分并被用于描述系统的不同状态。例如,如果一个系统可以处于状态∣0⟩|0\rangle∣0⟩或∣1⟩|1\rangle∣1⟩中,那么这两个态是正交的,因为它们的内积为0。
总之,正交归一化叠加态是指在一个量子系统中,多个归一化态之间是正交的,并且它们的叠加形成了一个新的归一化态。在量子计算中,正交归一化叠加态是一种常用的量子态,因为它们具有良好的可操作性和测量性质。常见的正交归一化叠加态包括Hadamard变换的超位置态和Bell态。
12(∣00⟩+∣11⟩)\frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)21(∣00⟩+∣11⟩):这是一个Bell态,也是一个常用的量子态。它可以通过将两个qubit都置于∣+⟩|+\rangle∣+⟩态并施加CNOT门来制备。
12(∣00⟩+∣01⟩)\frac{1}{\sqrt{2}}(|00\rangle + |01\rangle)21(∣00⟩+∣01⟩):这是一个比特的叠加态。它可以通过对一个qubit施加Hadamard门来制备。
相位(全局与相对)
全局相位
全局相位是指一个量子态的相位旋转,它不会改变该量子态的物理性质。在量子力学中,一个量子态可以表示成幺正算符作用于某个基态,而幺正算符通常包含一个相位因子。对于一个给定的量子态,如果我们对这个幺正算符中的相位进行一个统一的改变,那么这个量子态就会产生一个全局相位的变化。这个全局相位的变化不会影响任何可观测量的测量结果,因此被视为无用的信息。
一个例子是两个量子比特的纠缠态 ∣ψ⟩=12(∣01⟩−∣10⟩)|\psi\rangle = \frac{1}{\sqrt{2}}(|01\rangle - |10\rangle)∣ψ⟩=21(∣01⟩−∣10⟩),这个态有一个全局相位因子 −1-1−1,并且有一个相对相位因子 iii。
全局相位因子表现为态矢量整体乘上一个复数,比如 eiθe^{i\theta}eiθ,其中 θ\thetaθ 是一个常数。在上面的例子中,−1-1−1 就是这个态的全局相位因子。
相对相位因子表现为态矢量中不同基态系数之间的复数因子,比如上面的例子中的 iii。在这个例子中,∣01⟩|01\rangle∣01⟩ 和 ∣10⟩|10\rangle∣10⟩ 的系数之间的相对相位因子是 iii。
在量子力学中,一个态矢量 ∣ψ⟩|\psi\rangle∣ψ⟩ 可以表示为相对相位和全局相位的乘积形式:∣ψ⟩=eiγeiθ∣u⟩∣ψ⟩=e^{iγ}e^{iθ}|u⟩∣ψ⟩=eiγeiθ∣u⟩
其中 ∣u⟩|u\rangle∣u⟩ 是一个固定的态矢量,θ\thetaθ 是相对相位,γ\gammaγ 是全局相位。相对相位指的是相对于某个基态 ∣u⟩|u\rangle∣u⟩ 的相位,而全局相位是指整个态矢量的相位。
首先,假设我们有一个两量子比特的纯态 ∣ψ⟩|\psi\rangle∣ψ⟩,其中第一个量子比特的状态是 ∣0⟩|0\rangle∣0⟩,第二个量子比特的状态为
∣ψ2⟩=α∣0⟩+β∣1⟩.|\psi_2\rangle = \alpha|0\rangle + \beta|1\rangle.∣ψ2⟩=α∣0⟩+β∣1⟩.
假设我们在第一个量子比特上施加一个相位门 Rz(θ)R_z(\theta)Rz(θ),我们可以得到如下的纯态:
∣ψ′⟩=Rz(θ)∣ψ⟩=∣0⟩(α∣0⟩+βeiθ∣1⟩).|\psi'\rangle = R_z(\theta)|\psi\rangle = |0\rangle(\alpha|0\rangle + \beta e^{i\theta}|1\rangle).∣ψ′⟩=Rz(θ)∣ψ⟩=∣0⟩(α∣0⟩+βeiθ∣1⟩).
现在,我们来计算相对相位。设 ∣ψ1⟩=∣0⟩|\psi_1\rangle = |0\rangle∣ψ1⟩=∣0⟩,则
⟨ψ1∣ψ′⟩=⟨0∣0⟩(α⟨0∣0⟩+βeiθ⟨0∣1⟩)=α.\langle\psi_1|\psi'\rangle = \langle 0|0\rangle(\alpha\langle 0|0\rangle + \beta e^{i\theta}\langle 0|1\rangle) = \alpha.⟨ψ1∣ψ′⟩=⟨0∣0⟩(α⟨0∣0⟩+βeiθ⟨0∣1⟩)=α.
类似地,设 ∣ψ1⟩=∣1⟩|\psi_1\rangle = |1\rangle∣ψ1⟩=∣1⟩,则
⟨ψ1∣ψ′⟩=⟨1∣0⟩(α⟨0∣1⟩+βeiθ⟨1∣1⟩)=βeiθ.\langle\psi_1|\psi'\rangle = \langle 1|0\rangle(\alpha\langle 0|1\rangle + \beta e^{i\theta}\langle 1|1\rangle) = \beta e^{i\theta}.⟨ψ1∣ψ′⟩=⟨1∣0⟩(α⟨0∣1⟩+βeiθ⟨1∣1⟩)=βeiθ.
因此,我们可以得到相对相位为 θ\thetaθ。
现在,我们来看一个有全局相位的例子。假设我们的初始态为
∣ψ⟩=12(∣01⟩−∣10⟩).|\psi\rangle = \frac{1}{\sqrt{2}}(|01\rangle - |10\rangle).∣ψ⟩=21(∣01⟩−∣10⟩).
我们来计算施加相位门 Rz(θ)R_z(\theta)Rz(θ) 之后的态。首先,我们需要将 Rz(θ)R_z(\theta)Rz(θ) 展开成矩阵形式:
Rz(θ)=[e−iθ/200eiθ/2].R_z(\theta) = \begin{bmatrix} e^{-i\theta/2} & 0 \\ 0 & e^{i\theta/2} \end{bmatrix}.Rz(θ)=[e−iθ/200eiθ/2].
对第一个量子比特施加 Rz(θ)R_z(\theta)Rz(θ) 门后,我们得到的新态为:
∣ψ′⟩=12(e−iθ/2∣0⟩∣1⟩−eiθ/2∣1⟩∣0⟩).|\psi'\rangle = \frac{1}{\sqrt{2}}(e^{-i\theta/2}|0\rangle|1\rangle - e^{i\theta/2}|1\rangle|0\rangle).∣ψ′⟩=21(e−iθ/2∣0⟩∣1⟩−eiθ/2∣1⟩∣0⟩).
现在,我们来计算两个态的内积:
⟨ψ∣ψ′⟩=12[1−1][e−iθ/2−eiθ/2]=−12eiθ/2.\langle\psi|\psi'\rangle = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & -1 \end{bmatrix}\begin{bmatrix} e^{-i\theta/2} \ -e^{i\theta/2} \end{bmatrix} = -\frac{1}{\sqrt{2}}e^{i\theta/2}.⟨ψ∣ψ′⟩=21[1−1][e−iθ/2 −eiθ/2]=−21eiθ/2.
由于内积的结果中有相位 eiθ/2e^{i\theta/2}eiθ/2,所以我们称这个量子态有全局相位。全局相位是一个复数,它可以表示为θ=eiϕ\theta= e^{i\phi}θ=eiϕ,其中ϕ\phiϕ是相位角。当我们对一个量子比特施加一个全局相位θ\thetaθ时,其密度矩阵的形式会发生变化,但在测量方面并没有影响。因此,全局相位通常被认为是量子态的“不可观测量”。
考虑一个单量子比特系统的初始状态为∣ψ⟩=α∣0⟩+β∣1⟩|\psi\rangle=\alpha|0\rangle+\beta|1\rangle∣ψ⟩=α∣0⟩+β∣1⟩,其中α\alphaα和β\betaβ是复数且满足∣α∣2+∣β∣2=1|\alpha|^2+|\beta|^2=1∣α∣2+∣β∣2=1。假设我们施加一个全局相位θ=eiϕ\theta= e^{i\phi}θ=eiϕ,则量子态变为
∣ψ′⟩=eiϕ(α∣0⟩+β∣1⟩)|\psi'\rangle=e^{i\phi}(\alpha|0\rangle+\beta|1\rangle)∣ψ′⟩=eiϕ(α∣0⟩+β∣1⟩)
我们可以将这个量子态写成极坐标形式:
∣ψ′⟩=∣α∣ei(ϕ+θ1)∣0⟩+∣β∣ei(ϕ+θ2)∣1⟩|\psi'\rangle=|\alpha|e^{i(\phi+\theta_1)}|0\rangle+|\beta|e^{i(\phi+\theta_2)}|1\rangle∣ψ′⟩=∣α∣ei(ϕ+θ1)∣0⟩+∣β∣ei(ϕ+θ2)∣1⟩
其中,θ1\theta_1θ1和θ2\theta_2θ2是α\alphaα和β\betaβ的相位角,θ1+θ2=π\theta_1+\theta_2=\piθ1+θ2=π。
可以看出,全局相位θ\thetaθ只是改变了量子态中的全局相位,而不影响相对相位。因此,全局相位通常被忽略,因为它并不影响测量结果或量子计算中的其他操作。
相对相位
与全局相位相对的是相对相位,它指的是两个量子态之间的相对相位差异。
假设有两个量子态 ∣ψ1⟩|\psi_1\rangle∣ψ1⟩ 和 ∣ψ2⟩|\psi_2\rangle∣ψ2⟩,它们的全局相位是一样的,即它们都被乘上了同一个复数因子 eiθe^{i\theta}eiθ,其中 θ\thetaθ 是相位角度,那么这两个量子态可以表示为:
∣ψ1⟩=eiθ∣ϕ⟩|\psi_1\rangle=e^{i\theta}|\phi\rangle∣ψ1⟩=eiθ∣ϕ⟩
∣ψ1⟩=eiθ∣φ⟩|\psi_1\rangle=e^{i\theta}|\varphi\rangle∣ψ1⟩=eiθ∣φ⟩
其中 ∣ϕ⟩|\phi\rangle∣ϕ⟩ 和 ∣φ⟩|\varphi\rangle∣φ⟩ 是两个不同的量子态。如果我们现在对 ∣ψ1⟩|\psi_1\rangle∣ψ1⟩ 和 ∣ψ2⟩|\psi_2\rangle∣ψ2⟩ 进行测量,它们所对应的概率幅值的比值为:
⟨ψ1∣ψ2⟩∣⟨ψ1∣ψ2⟩∣=eiϕ\frac{\langle\psi_1|\psi_2\rangle}{|\langle\psi_1|\psi_2\rangle|}=e^{i\phi}∣⟨ψ1∣ψ2⟩∣⟨ψ1∣ψ2⟩=eiϕ
其中 ϕ\phiϕ 是 ∣ϕ⟩|\phi\rangle∣ϕ⟩ 和 ∣φ⟩|\varphi\rangle∣φ⟩ 之间的相对相位差。这个相对相位差是全局相位角度 θ\thetaθ 的函数,而不是 ∣ϕ⟩|\phi\rangle∣ϕ⟩ 和 ∣φ⟩|\varphi\rangle∣φ⟩ 的函数。因此,相对相位差是不受全局相位影响的,只与量子态 ∣ϕ⟩|\phi\rangle∣ϕ⟩ 和 ∣φ⟩|\varphi\rangle∣φ⟩ 有关。
因此,我们可以通过改变 ∣ϕ⟩|\phi\rangle∣ϕ⟩ 和 ∣φ⟩|\varphi\rangle∣φ⟩ 之间的相对相位差来改变它们之间的区别。这也就是为什么在量子计算中,相对相位非常重要,因为它可以被用来实现量子计算中的一些关键操作,比如量子傅里叶变换和量子相位估计。
总结一下,相对相位是不受全局相位影响的量子态之间的相位差,它可以被用来描述不同量子态之间的区别,并且在量子计算中有重要的应用。
相位反冲的例子
ex1)
∣+⟩=12(∣0⟩+∣1⟩)|+\rangle= \frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)∣+⟩=21(∣0⟩+∣1⟩)
0⊗∣+⟩=12(∣00⟩+∣01⟩)→CNOT-212(∣00⟩+∣11⟩)0\otimes|+\rangle= \frac{1}{\sqrt{2}}(|00\rangle+|01\rangle) \xrightarrow{\text{CNOT-2}} \frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)0⊗∣+⟩=21(∣00⟩+∣01⟩)CNOT-221(∣00⟩+∣11⟩)
Uf:12(∣00⟩+∣11⟩)→U12(∣0⟩(−1)f(0)∣0⟩+∣1⟩(−1)f(1)1⟩)U_f: \frac{1}{\sqrt{2}}(|00\rangle+|11\rangle) \xrightarrow{\text{U}} \frac{1}{\sqrt{2}}(|0\rangle(-1)^{f(0)}|0\rangle+|1\rangle(-1)^{f(1)}1\rangle)Uf:21(∣00⟩+∣11⟩)U21(∣0⟩(−1)f(0)∣0⟩+∣1⟩(−1)f(1)1⟩)
其中,∣0⟩|0\rangle∣0⟩ 和 ∣1⟩|1\rangle∣1⟩ 分别表示量子比特的基态,∣+⟩|+\rangle∣+⟩ 表示 ∣0⟩|0\rangle∣0⟩ 和 ∣1⟩|1\rangle∣1⟩ 的正交归一化叠加态,⊗\otimes⊗ 表示张量积,UfU_fUf 表示一个由 fff 定义的量子门,(−1)f(x)(-1)^{f(x)}(−1)f(x) 是一个复数相位,其取值为 +1+1+1 或 −1-1−1,具体取决于 f(x)f(x)f(x) 的值。即测量第一个量子比特的结果时,如果结果为∣0⟩|0\rangle∣0⟩ ,则说明第二位的结果也是∣0⟩|0\rangle∣0⟩ ,此时并没有对第二个量子位进行测量,但是我们知道了第二个量子位的信息。这就是因为我们将第二个量子位操作的变化反转到了全局相位的变化上。
ex2)
假设有一个单量子比特的初始态 ∣ψ⟩=∣0⟩|\psi\rangle = |0\rangle∣ψ⟩=∣0⟩,经过以下操作后进行测量得到结果 ∣1⟩|1\rangle∣1⟩:
将 ∣ψ⟩|\psi\rangle∣ψ⟩ 应用一个 Hadamard 门: H∣ψ⟩=12(∣0⟩+∣1⟩)H|\psi\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)H∣ψ⟩=21(∣0⟩+∣1⟩)。
将 ∣ψ⟩|\psi\rangle∣ψ⟩ 作为控制比特,将一个目标比特 ∣−⟩=12(∣0⟩−∣1⟩)|-\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)∣−⟩=21(∣0⟩−∣1⟩) 作为目标比特,进行 CNOT 操作: CNOT∣ψ⟩,∣−⟩12(∣0⟩∣−⟩+∣1⟩∣+⟩)CNOT_{|\psi\rangle,|-\rangle} \frac{1}{\sqrt{2}}(|0\rangle|-\rangle + |1\rangle|+\rangle)CNOT∣ψ⟩,∣−⟩21(∣0⟩∣−⟩+∣1⟩∣+⟩)。
测量第一个量子比特。如果测量结果为 ∣0⟩|0\rangle∣0⟩,则目标比特测量结果为 ∣−⟩|-\rangle∣−⟩;如果测量结果为 ∣1⟩|1\rangle∣1⟩,则目标比特测量结果为 ∣+⟩|+\rangle∣+⟩。
CNOT∣ψ⟩,∣−⟩12(∣0⟩∣−⟩+∣1⟩∣+⟩)=12(∣0⟩∣−⟩−∣1⟩∣+⟩)CNOT_{|\psi\rangle,|-\rangle}\frac{1}{\sqrt{2}}(|0\rangle|-\rangle + |1\rangle|+\rangle)=\frac{1}{\sqrt{2}}(|0\rangle|-\rangle - |1\rangle|+\rangle)CNOT∣ψ⟩,∣−⟩21(∣0⟩∣−⟩+∣1⟩∣+⟩)=21(∣0⟩∣−⟩−∣1⟩∣+⟩)
在这个例子中,相位反转发生在第 2 步,当控制比特 ∣ψ⟩|\psi\rangle∣ψ⟩ 的状态为 ∣1⟩|1\rangle∣1⟩ 时,目标比特的相位将反转。
ex3):一个复杂的例子
考虑一个双量子比特系统,其中第一个量子比特是控制量子比特,第二个量子比特是目标量子比特。假设目标量子比特处于状态 ∣u⟩|u\rangle∣u⟩,而控制量子比特处于状态 (∣0⟩+∣1⟩)/2(|0\rangle + |1\rangle) / \sqrt{2}(∣0⟩+∣1⟩)/2,即:
∣ψ⟩=12(∣0⟩+∣1⟩)∣u⟩|\psi\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)|u\rangle∣ψ⟩=21(∣0⟩+∣1⟩)∣u⟩
我们希望将目标量子比特的相位信息传递到控制量子比特上。为了实现这一目的,我们需要执行下面的操作:
- 用目标量子比特和一个第三个量子比特构成一个受控门。第三个量子比特的状态为 ∣−⟩|-\rangle∣−⟩,即 H∣−⟩=∣1⟩H|-\rangle = |1\rangleH∣−⟩=∣1⟩,X∣−⟩=−∣−⟩=∣−⟩X|-\rangle = -|-\rangle=|-\rangleX∣−⟩=−∣−⟩=∣−⟩。
- 将控制量子比特与第三个量子比特进行 CNOT 门操作。
- 将第三个量子比特和目标量子比特进行 CNOT 门操作(复原)。
- 再次将控制量子比特和第三个量子比特进行 CNOT 门操作(复原)。
下面是具体到公式的演示方法:
-
将目标量子比特 ∣u⟩|u\rangle∣u⟩ 与第三个量子比特 ∣−⟩|-\rangle∣−⟩ 进行 CNOT 门操作,得到如下状态:
∣+⟩∣u⟩∣−⟩→CNOT-2,312∣+⟩(∣u⟩−∣u⟩)|+\rangle|u\rangle|-\rangle \xrightarrow{\text{CNOT-2,3}} \frac{1}{\sqrt{2}}|+\rangle(|u\rangle-|u\rangle)∣+⟩∣u⟩∣−⟩CNOT-2,321∣+⟩(∣u⟩−∣u⟩) -
将控制量子比特 (∣0⟩+∣1⟩)/2(|0\rangle + |1\rangle) / \sqrt{2}(∣0⟩+∣1⟩)/2 与第三个量子比特 ∣−⟩|-\rangle∣−⟩ 进行 CNOT 门操作,得到如下状态:
12(∣0⟩+∣1⟩)(∣u⟩−∣u⟩)−12(∣0⟩−∣1⟩)(∣u⟩+∣u⟩)∣−⟩\frac{1}{2}(|0\rangle+|1\rangle)(|u\rangle-|u\rangle) - \frac{1}{2}(|0\rangle-|1\rangle)(|u\rangle+|u\rangle)|-\rangle21(∣0⟩+∣1⟩)(∣u⟩−∣u⟩)−21(∣0⟩−∣1⟩)(∣u⟩+∣u⟩)∣−⟩ -
将第三个量子比特 ∣−⟩|-\rangle∣−⟩ 与目标量子比特 ∣u⟩|u\rangle∣u⟩ 进行 CNOT 门操作,得到如下状态:
12(∣0⟩+∣1⟩)(∣u⟩−∣u⟩)−12(∣0⟩−∣1⟩)(∣u⟩−∣u⟩)∣−⟩\frac{1}{2}(|0\rangle+|1\rangle)(|u\rangle-|u\rangle) - \frac{1}{2}(|0\rangle-|1\rangle)(|u\rangle-|u\rangle)|-\rangle21(∣0⟩+∣1⟩)(∣u⟩−∣u⟩)−21(∣0⟩−∣1⟩)(∣u⟩−∣u⟩)∣−⟩ -
注意到此时,第二个量子比特 ∣u⟩|u\rangle∣u⟩ 的相位信息已经传递到第三个量子比特 ∣−⟩|-\rangle∣−⟩ 上了。最后,将控制量子比特 (∣0⟩+∣1⟩)/2(|0\rangle + |1\rangle) / \sqrt{2}(∣0⟩+∣1⟩)/2 与第三个量子比特 ∣−⟩|-\rangle∣−⟩ 再进行一次 CNOT 门操作,得到如下状态:
12(∣0⟩∣−⟩−∣1⟩∣−⟩)(∣u⟩−∣u⟩)−12(∣0⟩∣−⟩+∣1⟩∣−⟩)(∣u⟩−∣u⟩)\frac{1}{2}(|0\rangle|-\rangle-|1\rangle|-\rangle)(|u\rangle-|u\rangle) - \frac{1}{2}(|0\rangle|-\rangle+|1\rangle|-\rangle)(|u\rangle-|u\rangle)21(∣0⟩∣−⟩−∣1⟩∣−⟩)(∣u⟩−∣u⟩)−21(∣0⟩∣−⟩+∣1⟩∣−⟩)(∣u⟩−∣u⟩)
化简后可得:
12(∣0⟩−∣1⟩)∣u⟩\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)|u\rangle21(∣0⟩−∣1⟩)∣u⟩
可以看到,控制量子比特的相位信息已经被传递到了目标量子比特上,并且多了一个负号。这就是相位反转的效果。
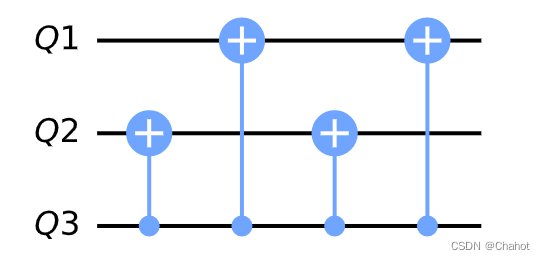
其中 Q1Q_1Q1 表示控制量子比特,Q2Q_2Q2 表示目标量子比特,Q3Q_3Q3 表示第三个量子比特。
在该电路中,我们首先对 Q2Q_2Q2 和 Q3Q_3Q3 进行受控门操作,使得 Q3Q_3Q3 的相位信息被传递到了 Q2Q_2Q2 上。然后,我们将 Q1Q_1Q1 和 Q3Q_3Q3 进行 CNOT 门操作,这相当于在 Q3Q_3Q3 的状态为 ∣1⟩|1\rangle∣1⟩ 的时候对 Q1Q_1Q1 进行了 XXX 门操作。接着,我们将 Q2Q_2Q2 和 Q3Q_3Q3 进行 CNOT 门操作,这将使得 Q1Q_1Q1 的相位信息被传递到了 Q3Q_3Q3 上。最后,我们再次将 Q1Q_1Q1 和 Q3Q_3Q3 进行 CNOT 门操作,相当于在 Q3Q_3Q3 的状态为 ∣1⟩|1\rangle∣1⟩ 的时候对 Q1Q_1Q1 进行了 XXX 门操作。这一系列操作的结果是,Q1Q_1Q1 的相位信息被传递到了 Q1Q_1Q1 本身上,也就是实现了相位反冲的效果。
这个过程中实现相位反冲的关键在于第二步和第四步的 CNOT 门操作。具体来说,第二步的 CNOT 门操作实现了对于 Q3Q_3Q3 在 ∣1⟩|1\rangle∣1⟩ 状态时,对 Q1Q_1Q1 的 XXX 门操作,而第四步的 CNOT 门操作实现了对于 Q3Q_3Q3 在 ∣1⟩|1\rangle∣1⟩ 状态时,再次对 Q1Q_1Q1 的 XXX 门操作。
当 Q2Q_2Q2 和 Q3Q_3Q3 进行受控门操作时,由于 Q3Q_3Q3 的初始状态为 ∣−⟩|-\rangle∣−⟩,所以相当于对 Q2Q_2Q2 应用了一个相位门操作 SSS。因此,我们实际上实现的是对 Q1Q_1Q1 应用了 SSS 门操作,将 Q2Q_2Q2 的相位信息反冲到了 Q1Q_1Q1 上。
然后在第二步和第四步的 CNOT 门操作中,当 Q3Q_3Q3 处于 ∣1⟩|1\rangle∣1⟩ 状态时,它会对 Q1Q_1Q1 施加一个 XXX 门操作,而当 Q3Q_3Q3 处于 ∣0⟩|0\rangle∣0⟩ 状态时,则不会对 Q1Q_1Q1 进行操作。因此,通过这两个 CNOT 门操作,我们可以将 Q2Q_2Q2 的相位信息反冲到 Q1Q_1Q1 上,实现了相位反冲的效果。
最终,我们得到的状态为 12(∣0⟩+eiϕ∣1⟩)∣u⟩\frac{1}{\sqrt{2}}(|0\rangle + e^{i\phi}|1\rangle)|u\rangle21(∣0⟩+eiϕ∣1⟩)∣u⟩,其中 ϕ\phiϕ 是 Q2Q_2Q2 的相位信息,已经被传递到了 Q1Q_1Q1 上。
为了更好地理解,我们将带入纯数式,用纯数学的方式来计算。
假设量子态 uuu 是一个单比特量子态,它的数学表达式可以表示为:
u=α∣0⟩+β∣1⟩u = \alpha |0\rangle + \beta |1\rangle u=α∣0⟩+β∣1⟩
其中,α\alphaα和β\betaβ是复数,∣0⟩|0\rangle∣0⟩和∣1⟩|1\rangle∣1⟩分别是基态。
另外,叠加态∣+⟩|+\rangle∣+⟩也是一个单比特量子态,它的数学表达式可以表示为:
∣+⟩=∣0⟩+∣1⟩2|+\rangle = \frac{|0\rangle + |1\rangle}{\sqrt{2}} ∣+⟩=2∣0⟩+∣1⟩
当叠加态 ∣+⟩|+\rangle∣+⟩ 作为控制比特,量子态 ∣0⟩|0\rangle∣0⟩ 作为目标比特,应用CNOT门,可以得到:
CNOT(∣+⟩∣0⟩)=CNOT(∣0⟩+∣1⟩2⊗∣0⟩)=∣00⟩+∣11⟩2\text{CNOT}(|+\rangle |0\rangle) = \text{CNOT}\left(\frac{|0\rangle + |1\rangle}{\sqrt{2}} \otimes |0\rangle\right) = \frac{|00\rangle + |11\rangle}{\sqrt{2}} CNOT(∣+⟩∣0⟩)=CNOT(2∣0⟩+∣1⟩⊗∣0⟩)=2∣00⟩+∣11⟩
因此,线路第二阶段与第四阶段输出的量子态可以表示为:
2阶段:∣α000⟩−∣α001⟩+∣α101⟩−∣α100⟩+∣β011⟩−∣β010⟩−∣β111⟩+∣β110⟩2=(∣0⟩∣u⟩−∣1⟩∣−u⟩)∣−⟩2阶段:\frac{|α000\rangle -|α001\rangle +|α101\rangle -|α100\rangle + |β011\rangle- |β010\rangle- |β111\rangle+ |β110\rangle}{2} =(|0\rangle|u\rangle-|1\rangle|-u\rangle)|-\rangle2阶段:2∣α000⟩−∣α001⟩+∣α101⟩−∣α100⟩+∣β011⟩−∣β010⟩−∣β111⟩+∣β110⟩=(∣0⟩∣u⟩−∣1⟩∣−u⟩)∣−⟩
4阶段:∣α000⟩−∣α001⟩+∣α100⟩−∣α101⟩−∣β011⟩+∣β010⟩+∣β110⟩−∣β111⟩2=(∣0⟩∣u⟩+∣1⟩∣u⟩)∣−⟩4阶段:\frac{|α000\rangle -|α001\rangle +|α100\rangle -|α101\rangle - |β011\rangle+ |β010\rangle+ |β110\rangle- |β111\rangle}{2} =(|0\rangle|u\rangle+|1\rangle|u\rangle)|-\rangle 4阶段:2∣α000⟩−∣α001⟩+∣α100⟩−∣α101⟩−∣β011⟩+∣β010⟩+∣β110⟩−∣β111⟩=(∣0⟩∣u⟩+∣1⟩∣u⟩)∣−⟩
2阶段公式化简可得:
(∣0⟩∣u⟩−∣1⟩∣−u⟩)∣−⟩=12∣0⟩(α∣0⟩+β∣1⟩)⊗∣−⟩−12∣1⟩(α∣0⟩−β∣1⟩)⊗∣−⟩=12(∣0⟩(α∣0⟩+β∣1⟩)−∣1⟩(α∣0⟩−β∣1⟩))⊗∣−⟩(|0\rangle|u\rangle-|1\rangle|-u\rangle)|-\rangle=\frac{1}{\sqrt{2}}|0\rangle(\alpha|0\rangle + \beta|1\rangle) \otimes |-\rangle - \frac{1}{\sqrt{2}}|1\rangle(\alpha|0\rangle - \beta|1\rangle) \otimes |-\rangle=\frac{1}{\sqrt{2}}(|0\rangle(\alpha|0\rangle + \beta|1\rangle)-|1\rangle(\alpha|0\rangle - \beta|1\rangle))\otimes |-\rangle (∣0⟩∣u⟩−∣1⟩∣−u⟩)∣−⟩=21∣0⟩(α∣0⟩+β∣1⟩)⊗∣−⟩−21∣1⟩(α∣0⟩−β∣1⟩)⊗∣−⟩=21(∣0⟩(α∣0⟩+β∣1⟩)−∣1⟩(α∣0⟩−β∣1⟩))⊗∣−⟩
而同理4阶段公式化简可得:
12(∣0⟩(α∣0⟩+β∣1⟩)+∣1⟩(α∣0⟩+β∣1⟩))⊗∣−⟩\frac{1}{\sqrt{2}}(|0\rangle(\alpha|0\rangle + \beta|1\rangle)+|1\rangle(\alpha|0\rangle + \beta|1\rangle))\otimes |-\rangle 21(∣0⟩(α∣0⟩+β∣1⟩)+∣1⟩(α∣0⟩+β∣1⟩))⊗∣−⟩
所以我们可以清楚的看到,量子反冲之前,当第一个量子位被测量后,我们无法得知第二个量子位的信息,它仍然是随机的。但是量子反冲之后,当第一个量子位被测量时,我们可以得知第二个量子位的相位信息。当第一个量子位确定时,第二个量子位也被确定了。
ex4)
假设三个量子比特分别为 q1q_1q1, q2q_2q2 和 q3q_3q3,并且目标量子比特 q3q_3q3 初始处于状态 ∣u⟩|u\rangle∣u⟩,而控制量子比特 q1q_1q1 初始处于状态 (∣0⟩+∣1⟩)/2(|0\rangle + |1\rangle) / \sqrt{2}(∣0⟩+∣1⟩)/2,其余量子比特初始处于状态 ∣0⟩|0\rangle∣0⟩。则该过程可以表达为以下一系列的门操作:
将第三个量子比特 q3q_3q3 应用一个 RzR_zRz 旋转门,将其相位翻转 180∘180^{\circ}180∘,即 Rz(π)∣u⟩=−∣u⟩R_z(\pi)|u\rangle = -|u\rangleRz(π)∣u⟩=−∣u⟩。
将 q1q_1q1 和一个辅助量子比特 q2q_2q2 进行 CNOT 门操作,得到状态:12(∣0⟩∣0⟩+∣1⟩∣1⟩)∣u⟩\frac{1}{\sqrt{2}}(|0\rangle|0\rangle + |1\rangle|1\rangle)|u\rangle21(∣0⟩∣0⟩+∣1⟩∣1⟩)∣u⟩
将 q2q_2q2 应用一个 HHH 门,得到状态:12(∣0⟩∣0⟩+∣1⟩∣1⟩)12(∣0⟩−∣1⟩)∣u⟩\frac{1}{\sqrt{2}}(|0\rangle|0\rangle + |1\rangle|1\rangle)\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)|u\rangle21(∣0⟩∣0⟩+∣1⟩∣1⟩)21(∣0⟩−∣1⟩)∣u⟩
将 q2q_2q2 和 q3q_3q3 进行 CNOT 门操作,得到状态:12(∣0⟩∣0⟩+∣1⟩∣1⟩)12(∣0⟩−∣1⟩)(∣u⟩−∣u′⟩)\frac{1}{\sqrt{2}}(|0\rangle|0\rangle + |1\rangle|1\rangle)\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)(|u\rangle - |u'\rangle)21(∣0⟩∣0⟩+∣1⟩∣1⟩)21(∣0⟩−∣1⟩)(∣u⟩−∣u′⟩) 其中,∣u′⟩|u'\rangle∣u′⟩ 表示经过 RzR_zRz 门操作后的目标量子比特状态。
将 q1q_1q1 和 q2q_2q2 再次进行 CNOT 门操作,得到状态:12(∣0⟩∣u⟩−∣1⟩∣u′⟩)12(∣0⟩−∣1⟩)\frac{1}{\sqrt{2}}(|0\rangle|u\rangle - |1\rangle|u'\rangle) \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)21(∣0⟩∣u⟩−∣1⟩∣u′⟩)21(∣0⟩−∣1⟩)
将 q2q_2q2 再次应用一个 HHH 门,得到状态:12[(∣0⟩−∣1⟩)(∣u⟩−∣u′⟩)]\frac{1}{2}[(|0\rangle - |1\rangle)(|u\rangle - |u'\rangle)]21[(∣0⟩−∣1⟩)(∣u⟩−∣u′⟩)]
最后,将 q1q_1q1 和 q2q_2q2 进行一次 CNOT 门操作,得到状态:12[(∣0⟩−∣1⟩)(∣u⟩−∣u′⟩)]∣0⟩+12[(∣0⟩+∣1⟩)(∣u⟩+∣u′⟩)]∣1⟩\frac{1}{2}[(|0\rangle - |1\rangle)(|u\rangle - |u'\rangle)]|0\rangle + \frac{1}{2}[(|0\rangle + |1\rangle)(|u\rangle + |u'\rangle)]|1\rangle21[(∣0⟩−∣1⟩)(∣u⟩−∣u′⟩)]∣0⟩+21[(∣0⟩+∣1⟩)(∣u⟩+∣u′⟩)]∣1⟩
我们可以看到,最终的状态中,第一个量子比特 q1q_1q1 上的相位信息反转了,并且通过观察第二个量子比特 q2q_2q2 的状态可以验证这一点。
相位反转与量子振幅放大算法
相位反转和相位反冲是两个不同的概念。相位反转通常是指改变一个量子态中某个比特的相位,即在Bloch球的经典视角下绕Z轴旋转一个角度,或者在复数表示下将相位取负。相位反转是一种常见的量子门操作,可以用于量子计算中的一些算法,如量子振幅放大算法。相位反冲是指一个比特的相位被反转后,与之相邻的另一个比特的相位也随之发生反转。在量子计算中,相位反冲可以用于制备纠缠态和量子错误校正等。
用目标量子比特和一个第三个量子比特构成一个受控门。第三个量子比特的状态为 ∣−⟩|-\rangle∣−⟩,即 H∣−⟩=∣1⟩H|-\rangle = |1\rangleH∣−⟩=∣1⟩,X∣−⟩=∣−⟩X|-\rangle = |-\rangleX∣−⟩=∣−⟩。
将控制量子比特与第三个量子比特进行 CNOT 门操作。
将第三个量子比特和目标量子比特进行 CNOT 门操作。
再次将控制量子比特和第三个量子比特进行 CNOT 门操作。
α∣0⟩control∣u⟩target+β∣1⟩control∣u⟩target→α∣0⟩control∣u⟩target+β∣1⟩control(−1)u∣u⟩targetα|0\rangle_{control}|u\rangle_{target}+β|1\rangle_{control}|u\rangle_{target} \rightarrow α|0\rangle_{control}|u\rangle_{target}+β|1\rangle_{control}(-1)^u|u\rangle_{target}α∣0⟩control∣u⟩target+β∣1⟩control∣u⟩target→α∣0⟩control∣u⟩target+β∣1⟩control(−1)u∣u⟩target
其中,α\alphaα 和 β\betaβ 是控制量子比特的两个状态。在这个过程中,第三个量子比特的相位翻转被“反弹”回控制量子比特,从而将目标量子比特的相位信息传递给控制量子比特。
相位反转(phase flip)和概率有一定的关系,因为在进行相位反转操作时,会导致量子态的相位发生改变,从而影响到测量时的概率分布。
∣0⟩control∣u⟩target→∣0⟩control(−1)u∣u⟩target|0\rangle_{control}|u\rangle_{target} \rightarrow |0\rangle_{control}(-1)^u|u\rangle_{target}∣0⟩control∣u⟩target→∣0⟩control(−1)u∣u⟩target
具体来说,在量子力学中,一个量子态可以表示为幅度和相位的叠加。在测量量子态时,它会坍缩为一个确定的状态,且不同状态的概率分布由幅度的模长的平方给出。相位反转操作本身不会增加概率,因为量子态的模长平方代表的概率在相位反转后不会改变。但是在某些情况下,相位反转操作可以通过干涉的方式增加某些测量结果的概率。
量子振幅放大算法
假设有一个黑盒子程序 UUU,它能将输入 xxx 映射到输出 f(x)f(x)f(x),其中 fff 是 nnn 比特的布尔函数,且保证只有一个 xxx 使得 f(x)=1f(x) = 1f(x)=1。我们的目标是找到这个满足 f(x)=1f(x) = 1f(x)=1 的 xxx。对于经典计算机而言,需要进行 2n2^n2n 次计算才能找到这个解,但对于量子计算机,量子振幅放大算法可以实现在 O(N)O(\sqrt{N})O(N) 次计算内找到这个解,其中 N=2nN = 2^nN=2n。
算法的流程如下:
初始化:对于一个函数f(x)f(x)f(x),我们选择一个初始状态∣s⟩\vert s \rangle∣s⟩和一个目标状态∣t⟩\vert t \rangle∣t⟩,并构造一个等概率的叠加态∣ψ⟩=1N∑x=0N−1∣x⟩\vert \psi \rangle = \frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}\vert x \rangle∣ψ⟩=N1∑x=0N−1∣x⟩,其中NNN是状态的总数。这里我们假设NNN是2n2^n2n,其中nnn是量子比特数。
反演操作:我们定义一个标记算符UtU_tUt,使得对于所有的xxx,Ut∣x⟩=(−1)f(x)∣x⟩U_t\vert x \rangle = (-1)^{f(x)}\vert x \rangleUt∣x⟩=(−1)f(x)∣x⟩,其中f(x)=1f(x) = 1f(x)=1当且仅当x=tx=tx=t,否则f(x)=0f(x)=0f(x)=0。我们将标记算符UtU_tUt分解成两个操作:首先对于所有的xxx,将∣x⟩\vert x \rangle∣x⟩映射到∣x⟩\vert x \rangle∣x⟩或−∣x⟩-\vert x \rangle−∣x⟩上,然后将−∣t⟩-\vert t \rangle−∣t⟩映射到∣t⟩\vert t \rangle∣t⟩上。这样,我们就得到了一个反演算符UsU_sUs,使得Us∣ψ⟩=1N∑x=0N−1(−1)s(x)∣x⟩U_s \vert \psi \rangle = \frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}(-1)^{s(x)}\vert x \rangleUs∣ψ⟩=N1∑x=0N−1(−1)s(x)∣x⟩,其中s(x)=1s(x) = 1s(x)=1当且仅当x≠tx \neq tx=t,否则s(x)=−1s(x) = -1s(x)=−1。
重复操作:我们将反演算符UsU_sUs应用kkk次,得到∣ψ′⟩=Usk∣ψ⟩\vert \psi' \rangle = U_s^k \vert \psi \rangle∣ψ′⟩=Usk∣ψ⟩。这里kkk的取值应该足够大,满足4karcsin1N≈π24k \arcsin \frac{1}{\sqrt{N}} \approx \frac{\pi}{2}4karcsinN1≈2π,其中arcsin\arcsinarcsin是反正弦函数。这样可以使得∣ψ′⟩\vert \psi' \rangle∣ψ′⟩更加靠近目标状态∣t⟩\vert t \rangle∣t⟩。
测量操作:最后我们进行一次测量操作,将∣ψ′⟩\vert \psi' \rangle∣ψ′⟩映射到某个状态上。由于∣ψ′⟩\vert \psi' \rangle∣ψ′⟩更加靠近目标状态∣t⟩\vert t \rangle∣t⟩,所以测量结果为∣t⟩\vert t \rangle∣t⟩的概率更大。
相关文章:

详解量子计算:相位反冲与相位反转
前言 本文需要对量子计算有一定的了解。需要的请翻阅我的量子专栏,这里不再涉及基础知识的科普。 量子相位反冲是什么? 相位反转(phase kickback)是量子计算中的一种现象,通常在量子算法中使用,例如量子…...
C++——C++11第三篇
目录 包装器 function包装器 bind 包装器 function包装器 function包装器 也叫作适配器。C中的function本质是一个类模板,也是一个包装器。 上面的程序验证,我们会发现useF函数模板实例化了三份。 包装器可以很好的解决上面的问题 ,让它只实…...

180 2 22222
选择题(共180题,合计180.0分) 1. 在项目开工会议期间,项目发起人告诉产品负责人和团队项目章程即将完成。然而,由于存在在紧迫的期限内满足政府监管要求的压力,发起人希望立即开始工作。产品负责人下一步应该做什么? A 告诉发起人…...

成人高考初中毕业能报名吗 需要什么条件
初中学历的人员不能直接报名成人高考,考生需要有普通高中,职业高中,中专毕业证等高中同等学力就可以进行报名,在报名期间登陆所在省的教育考试院的成人高考报名入口进行报考。成人高考报名条件是什么1、遵守宪法和法律。2、国家承…...

ChatGPT初体验
ChatGPT初体验 前言 嘿嘿,最近啊AI ChatGPT刷新各大网站,对于我们国人而将很不友好,真的太不友好了。我呢在去年open AI发布的时候就有所关注,那个时候还没有像现在这样火热。谁知道短短几个月便传遍大街小巷。 一、什么是chatG…...

ChatGPT概念狂飙!究竟魅力何在?
原文:http://www.btcwbo.com/6988.html 近期,ChatGPT引领的人工智能概念在资本市场一路狂飙,AIGC题材持续发酵。截至2月7日,Wind ChatGPT指数今年以来累计上涨超50%,汉王科技、海天瑞声、云从科技等概念股股价已经翻倍…...
如何下载阅读Spring源码-全过程详解
这篇文章记录了下载spring源码和在IDEA中打开运行的全过程,并且记录了过程中遇到的问题和解决方案,适合需要学习spring源码的同学阅读。 1.spring源码下载地址 通过Git下载spring-framework项目源码: git clone https://github.com/spring…...
学了两个月的Java,最后自己什么也不会,该怎么办?
学着学着你会发现每天的知识都在更新,也都在遗忘,可能就放弃了。但是只要自己肯练,肯敲代码,学过的知识是很容易就被捡起来的。等你学透了用不了一年也可以学好 Java的运行原理:Java是一门编译解释型语言,…...
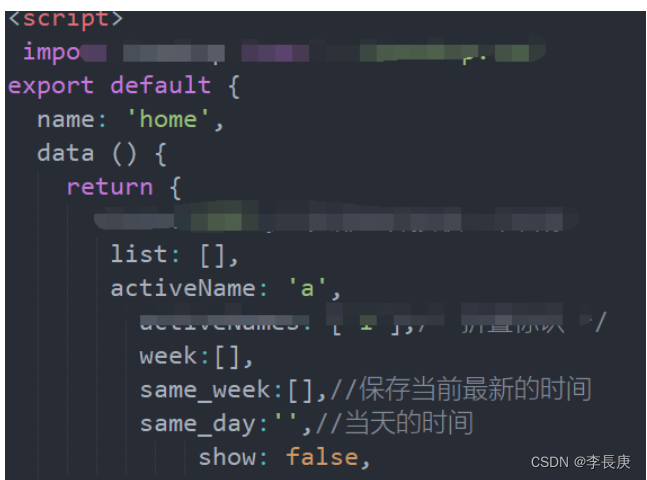
前端vue实现获取七天时间和星期几功能
前端vue实现获取七天时间和星期几功能 功能展示代码 <div v-for"(item,index) in same_week" :class"[same_dayitem.date? activ :,dis]" click"select(item)" :keyindex><span>{{item.name}}</span><span>{{item.…...

zookeeper单机部署
一.下载zookeeper压缩包 二.上传解压安装包到/data/zookeeper目录,并解压 tar -zxvf apache-zookeeper-3.5.8-bin.tar.gz 三.修改配置文件 cd apache-zookeeper-3.5.10-bin/conf mv zoo_sample.cfg zoo.cfg vi zoo.cfg 修改为如下: dataDir/data/zooke…...

单片机输入输出模式
单片机输入输出模式输入模式模拟输入、浮空输入、上拉输入、下拉输入GPIO输出模式推挽输出、开漏输出、复用推挽输出、复用开漏输出。上下拉电阻上拉电阻下拉电阻输入模式 模拟输入、浮空输入、上拉输入、下拉输入 模拟输入:I/O端口的模拟信号(电压信号…...
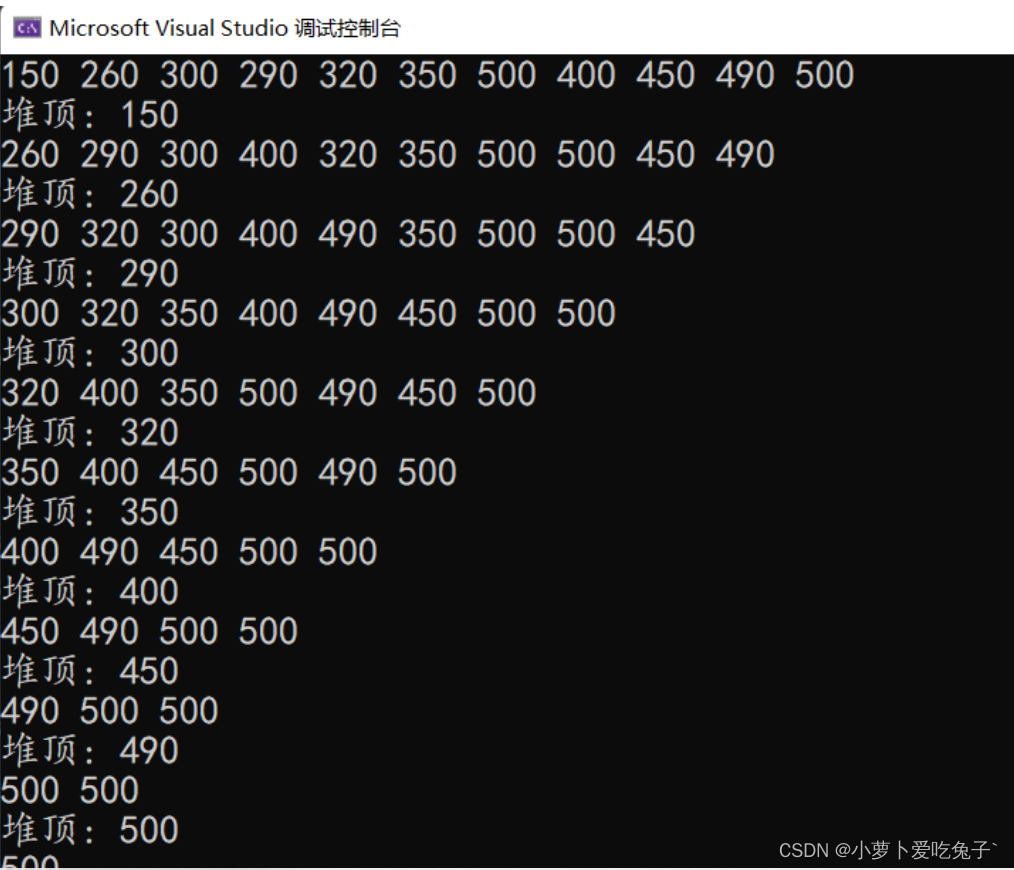
数据结构_ 堆结构与堆排序(c++ 实现 + 完整代码 )
堆结构与堆排序 文章目录堆结构与堆排序引入堆堆结构所满足的数学特性准备代码----------- 往堆中插入元素----------- 删除堆顶堆排序构建完整代码及测试动态分配版本非动态版本引入堆 二叉树 具有左孩子与右孩子的最普通的二叉树。 满二叉树 特殊的二叉树:每个节…...
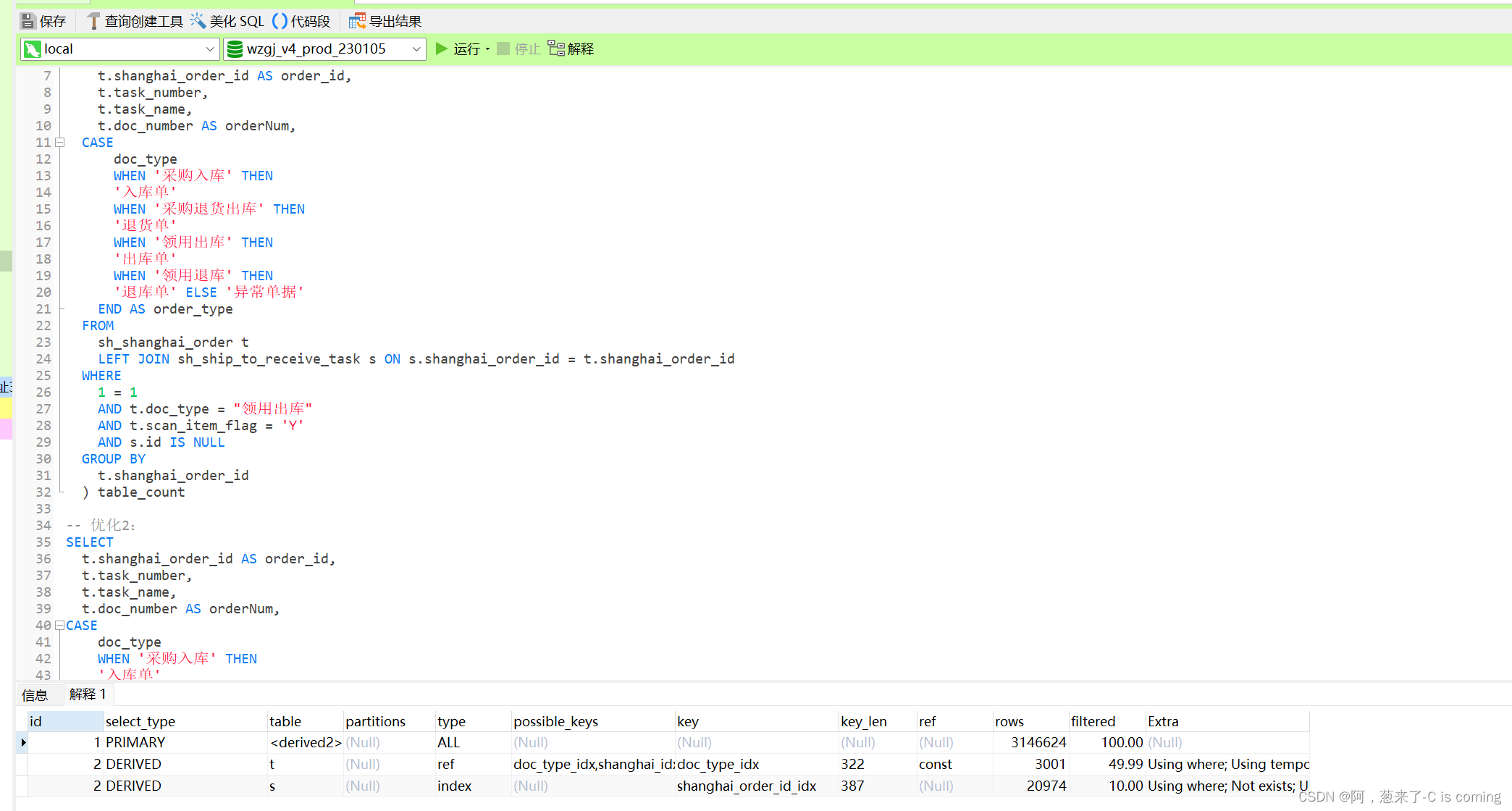
【MySQL】sql中explain解释和应用
这里写目录标题学习原因MySQL中explain的使用和用法解释explain的使用explain 运行结果的意义文字展示表格展示参考资料:结束语学习原因 在对sql的优化过程中使用了explain对指定的sql进行查看它的运行效果,以便找出sql的性能特点并进行优化 MySQL中ex…...
从零实现深度学习框架:Seq2Seq从理论到实战【实战篇】
来源:投稿 作者:175 编辑:学姐 往期内容: 从零实现深度学习框架1:RNN从理论到实战(理论篇) 从零实现深度学习框架2:RNN从理论到实战(实战篇) 从零实现深度…...

【数据结构入门】-链表之单链表(1)
个人主页:平行线也会相交 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【数据结构初阶(C实现)】 文章标题回顾链表链表的概念及结构各种节点打印链表尾插创建节点尾删头插头删查找在pos…...
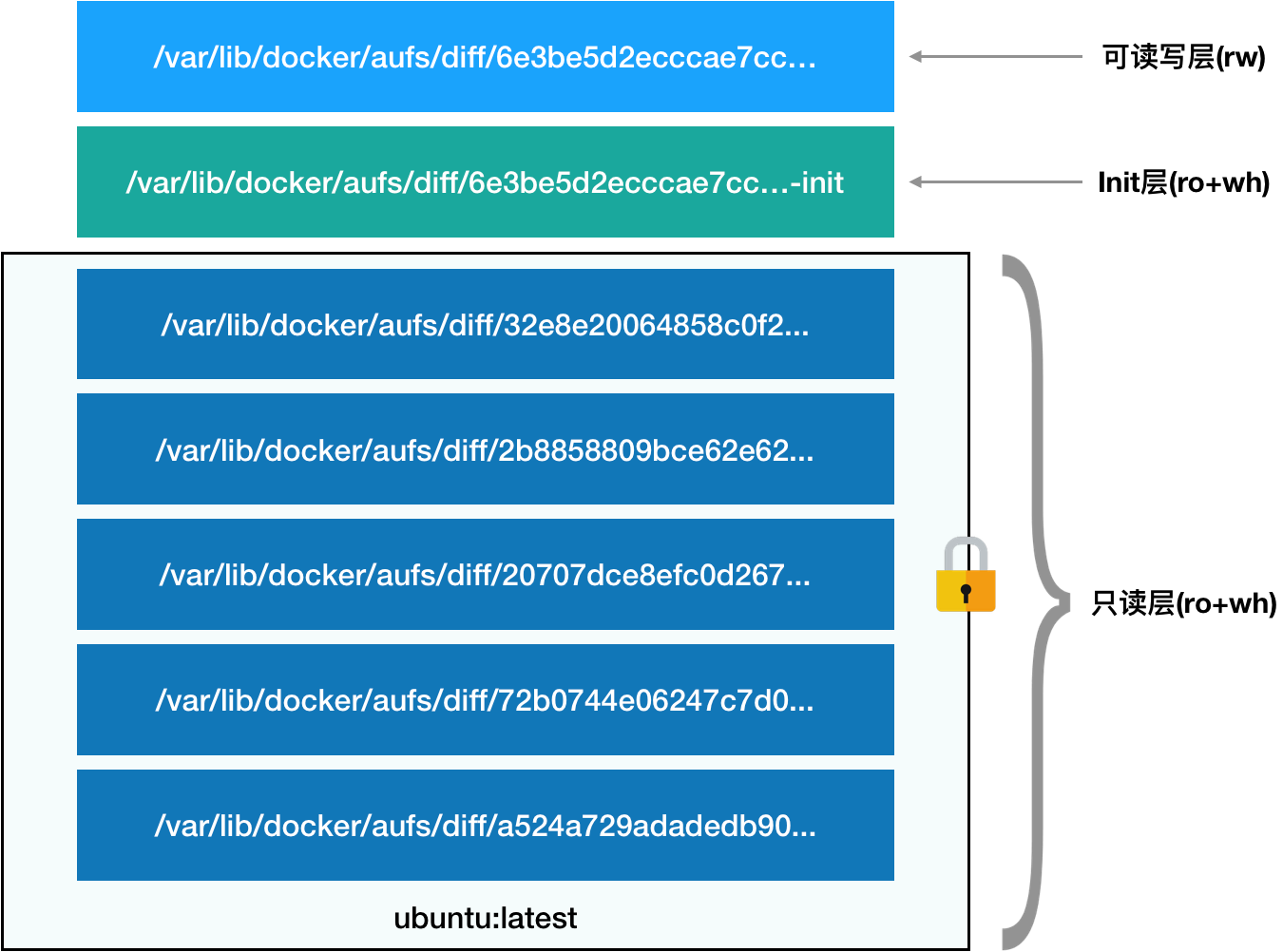
Docker竟如此简单!
文章目录什么是容器?容器隔离何为“边界”?容器和虚拟机一样吗?基于 Linux Namespace 隔离机制的弊端容器限制何为“限制”?Cgroups 对资源的限制能力缺陷单进程模型容器镜像容器的诞生容器的一致性何为“层(layer&…...
在外包干了几年,感觉自己都快费了
先说一下自己的情况。大专生,18年通过校招进入湖南某软件公司,干了接近2年的点点点,今年年上旬,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了五年的功能测试…...
Java实现多线程有几种方式(满分回答)
目录JDK8 创建的线程的两种方式orcle文档解释方式一:继承Thread类方式二:实现Runnable接口同时用两种的情况其他间接创建方式Callable接口线程池JDK8 创建的线程的两种方式 orcle文档解释 orcle文档:https://docs.oracle.com/javase/8/docs…...

实例4:树莓派GPIO控制舵机转动
实例4:树莓派GPIO控制舵机转动 实验目的 通过背景知识学习,了解舵机的外观及基本运动方式。了解四足机器人mini pupper腿部单个舵机的组成结构。通过GPIO对舵机进行转动控制,熟悉PWM。了解mini pupper舵机组的整体调零。 实验要求 使用Py…...

【音视频处理】为什么MP3不是无损音乐?音频参数详解,码率、采样率、音频帧、位深度、声道、编码格式的关系
大家好,欢迎来到停止重构的频道。上期我们讨论了视频的相关概念,本期我们讨论音频的相关概念。包括采样率、码率、单双声道、音频帧、编码格式等概念。这里先抛出一个关于无损音频的问题。为什么48KHz采样率的.mp3不是无损音乐 ,而48KHz采样率…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
