0401不定积分的概念和性质-不定积分
文章目录
- 1 原函数与不定积分的概念
- 1.1 原函数
- 1.2 原函数存在定理
- 1.3 不定积分
- 2 不定积分的性质
- 3 基本积分表
- 4 例题
- 后记
1 原函数与不定积分的概念
1.1 原函数
定义1 如果在区间I上,可导函数F(x)的导航为f(x),即对任一x∈Ix\in Ix∈I,都有
F′(x)=f(x)或者dF(x)=f(x)dxF^{'}(x)=f(x)或者dF(x)=f(x)dxF′(x)=f(x)或者dF(x)=f(x)dx,
那么函数F(x)就称为f(x)(或者f(x)dxf(x)dxf(x)dx)在区间I上的一个原函数。
1.2 原函数存在定理
原函数存在定理 如果函数f(x)在区间I上连续,那么在区间I存在可导函数F(x),使得对于任一x∈Ix\in Ix∈I都有
F′(x)=f(x)F^{'}(x)=f(x)F′(x)=f(x)
连续函数一定有原函数
- 如果f(x)有一个原函数,那么f(x)就有无限多个原函数
- F(x)+CF(x)+CF(x)+C可以表示f(x)f(x)f(x)的任意一个原函数,其中C为任意常数
1.3 不定积分
定义2 在区间I上,函数f(x)f(x)f(x)的带有任意常数项的原函数称为f(x)(或f(x)dx)f(x)(或f(x)dx)f(x)(或f(x)dx)在区间I上的不定积分,记做
∫f(x)dx\int{f(x)dx}∫f(x)dx
其中∫\int∫称为积分号,f(x)f(x)f(x)称为被积函数,f(x)dxf(x)dxf(x)dx称为被积表达式,x称为积分变量。
注:
- 若F(x)为f(x)F(x)为f(x)F(x)为f(x)的一个原函数,则∫f(x)dx=F(x)+C\int{f(x)dx}=F(x)+C∫f(x)dx=F(x)+C,其中C为任意常数。
- ∫f(x)dx\int{f(x)dx}∫f(x)dx表示f(x)f(x)f(x)的任意一个原函数,是一种运算。
例2 求∫1xdx\int \frac{1}{x}dx∫x1dx
解:当x>0时,(lnx)′=1x,所以∫1xdx=lnx+C当x<0时,(ln(−x))′=1−x⋅−1=1x,∫1xdx=ln(−x)+C综上∫1xdx=ln∣x∣+C解:\\ 当x\gt0时,(\ln x)^{'}=\frac{1}{x},所以\int \frac{1}{x}dx=\ln x+C \\ 当x\lt0时,(\ln(-x))^{'}=\frac{1}{-x}\cdot-1=\frac{1}{x},\int \frac{1}{x}dx=\ln(-x)+C \\ 综上\int \frac{1}{x}dx=\ln|x|+C \\ 解:当x>0时,(lnx)′=x1,所以∫x1dx=lnx+C当x<0时,(ln(−x))′=−x1⋅−1=x1,∫x1dx=ln(−x)+C综上∫x1dx=ln∣x∣+C
2 不定积分的性质
设F(x)为f(x)在区间I上的一个原函数
性质1 d[∫f(x)dx]dx=f(x)或d[∫f(x)dx]=f(x)dx\frac{d[\int f(x)dx]}{dx}=f(x)或 d[\int f(x)dx]=f(x)dxdxd[∫f(x)dx]=f(x)或d[∫f(x)dx]=f(x)dx
性质2 ∫F′(x)dx=F(x)+C或∫dF(x)=F(x)+C\int F^{'}(x)dx=F(x)+C或\int dF(x)=F(x)+C∫F′(x)dx=F(x)+C或∫dF(x)=F(x)+C
性质3 设函数f(x)及g(x)的原函数存在,则
∫[f(x)+g(x)]dx=∫f(x)dx+∫g(x)dx\int{[f(x)+g(x)]dx}=\int{f(x)dx}+\int{g(x)dx}∫[f(x)+g(x)]dx=∫f(x)dx+∫g(x)dx
证明:上式右端求导,[∫f(x)dx+∫g(x)dx]′=[∫f(x)dx]′+[∫g(x)dx]′=f(x)+g(x)所以右端也是f(x)+g(x)的不定积分证明:\\ 上式右端求导,[\int{f(x)dx}+\int{g(x)dx}]^{'}=[\int{f(x)dx}]^{'}+[\int{g(x)dx}]^{'}\\ =f(x)+g(x) \\ 所以右端也是f(x)+g(x)的不定积分 证明:上式右端求导,[∫f(x)dx+∫g(x)dx]′=[∫f(x)dx]′+[∫g(x)dx]′=f(x)+g(x)所以右端也是f(x)+g(x)的不定积分
注:性质3对于有限个函数都是成立的。
性质4 设函数f(x)的原函数存在,kkk为非零常数,则
∫kf(x)dx=k∫f(x)dx\int{kf(x)dx}=k\int{f(x)dx}∫kf(x)dx=k∫f(x)dx
3 基本积分表
①$\int{kdx}=kx+C $
②∫xudx=xu+1u+1+C\int{x^udx}=\frac{x^{u+1}}{u+1}+C∫xudx=u+1xu+1+C ③∫dxx=ln∣x∣+C\int{\frac{dx}{x}}=\ln|x|+C∫xdx=ln∣x∣+C
④∫11+x2dx=arctanx+C\int{\frac{1}{1+x^2}dx}=\arctan x+C∫1+x21dx=arctanx+C ⑤∫11−x2dx=arcsinx+C\int{\frac{1}{\sqrt{1-x^2}}dx}=\arcsin x+C∫1−x21dx=arcsinx+C
⑥∫cosxdx=sinx+C\int{\cos xdx}=\sin x+C∫cosxdx=sinx+C ⑦∫sinxdx=−cosx+C\int{\sin xdx}=-\cos x+C∫sinxdx=−cosx+C
⑧∫1sin2xdx=∫sec2xdx=tanx+C\int{\frac{1}{\sin^2x}dx}=\int{\sec^2xdx}=\tan x+C∫sin2x1dx=∫sec2xdx=tanx+C ⑨∫1cos2xdx=∫csc2xdx=−cotx+C\int{\frac{1}{\cos^2x}dx}=\int{\csc^2xdx}=-\cot x+C∫cos2x1dx=∫csc2xdx=−cotx+C
⑩∫secxtanxdx=secx+C\int{\sec x\tan xdx}=\sec x+C∫secxtanxdx=secx+C ⑪∫cscxcotxdx=−cscx+C\int{\csc x\cot xdx}=-\csc x+C∫cscxcotxdx=−cscx+C
⑫∫exdx=ex+C\int{e^xdx}=e^x+C∫exdx=ex+C ⑬∫axdx=axlna+C\int{a^xdx}=\frac{a^x}{\ln a}+C∫axdx=lnaax+C
4 例题
例1 ∫(x−1)3x2dx\int{\frac{(x-1)^3}{x^2}dx}∫x2(x−1)3dx
解:∫(x−1)3x2dx=∫x3−3x2+3x−1x2=∫xdx−∫3dx+∫3x−∫1x2=12x2−3x+3ln∣x∣+1x+C解:\\ \int{\frac{(x-1)^3}{x^2}dx}=\int{\frac{x^3-3x^2+3x-1}{x^2}}\\ =\int{xdx}-\int{3dx}+\int{\frac{3}{x}}-\int{\frac{1}{x^2}}\\ =\frac{1}{2}x^2-3x+3\ln|x|+\frac{1}{x}+C 解:∫x2(x−1)3dx=∫x2x3−3x2+3x−1=∫xdx−∫3dx+∫x3−∫x21=21x2−3x+3ln∣x∣+x1+C
例2 ∫2x4+x2+3x2+1dx\int{\frac{2x^4+x^2+3}{x^2+1}dx}∫x2+12x4+x2+3dx
解:利用多项式相除,得2x2+1,余4,有∫2x4+x2+3x2+1dx=∫(2x2−1+4x2+1)dx=∫2x2dx−∫1dx+∫4x2+1dx=2x33−x+4arctanx+C解:\\ 利用多项式相除,得2x^2+1,余4,有\\ \int{\frac{2x^4+x^2+3}{x^2+1}dx}=\int{(2x^2-1+\frac{4}{x^2+1})dx}\\ =\int{2x^2dx}-\int{1dx}+\int{\frac{4}{x^2+1}dx}=\frac{2x^3}{3}-x+4\arctan x+C 解:利用多项式相除,得2x2+1,余4,有∫x2+12x4+x2+3dx=∫(2x2−1+x2+14)dx=∫2x2dx−∫1dx+∫x2+14dx=32x3−x+4arctanx+C
多项式相除,如下图4-1所示: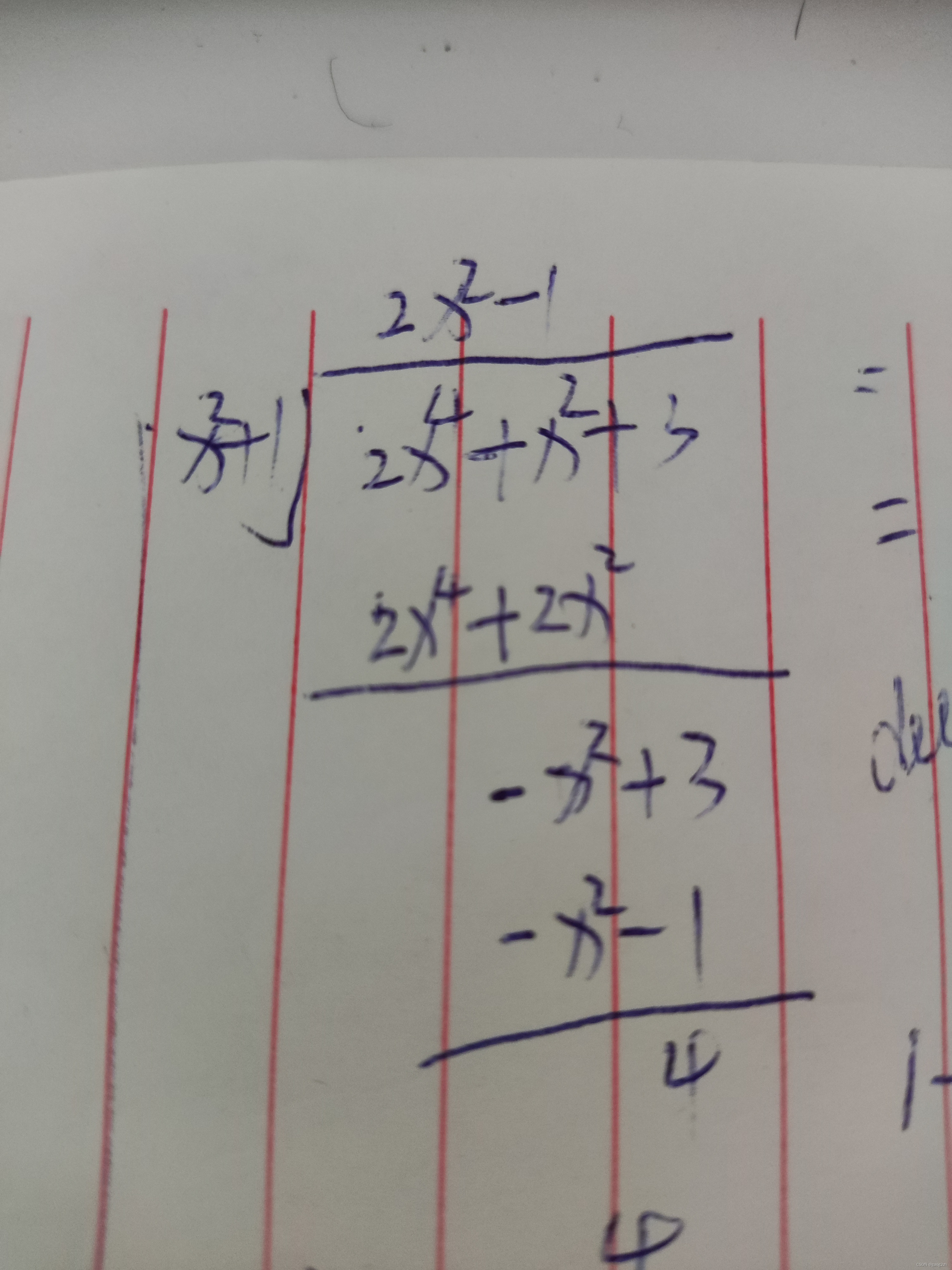
后记
❓QQ:806797785
⭐️文档笔记地址:https://gitee.com/gaogzhen/math
参考:
[1]同济大学数学系.高等数学 第七版 上册[M].北京:高等教育出版社,2014.7.P184~p193.
[2]【梨米特】同济七版《高等数学》全程教学视频|纯干货知识点解析,应该是全网最细|微积分 | 高数[CP/OL].2020-04-16.p27.
相关文章:

0401不定积分的概念和性质-不定积分
文章目录1 原函数与不定积分的概念1.1 原函数1.2 原函数存在定理1.3 不定积分2 不定积分的性质3 基本积分表4 例题后记1 原函数与不定积分的概念 1.1 原函数 定义1 如果在区间I上,可导函数F(x)的导航为f(x),即对任一x∈Ix\in Ix∈I,都有 F′…...

数组中的各种迭代API方法手写
js的数组上有很多实用的方法,不论是在遍历数组上,还是在操作数组内元素上,它有许多不同的遍历数组的方法,同时它还有着可以直接操作数组中间元素的方法。 接下来,我来带大家手写数组里的 遍历方法 。 Array.forEach(…...
详解量子计算:相位反冲与相位反转
前言 本文需要对量子计算有一定的了解。需要的请翻阅我的量子专栏,这里不再涉及基础知识的科普。 量子相位反冲是什么? 相位反转(phase kickback)是量子计算中的一种现象,通常在量子算法中使用,例如量子…...
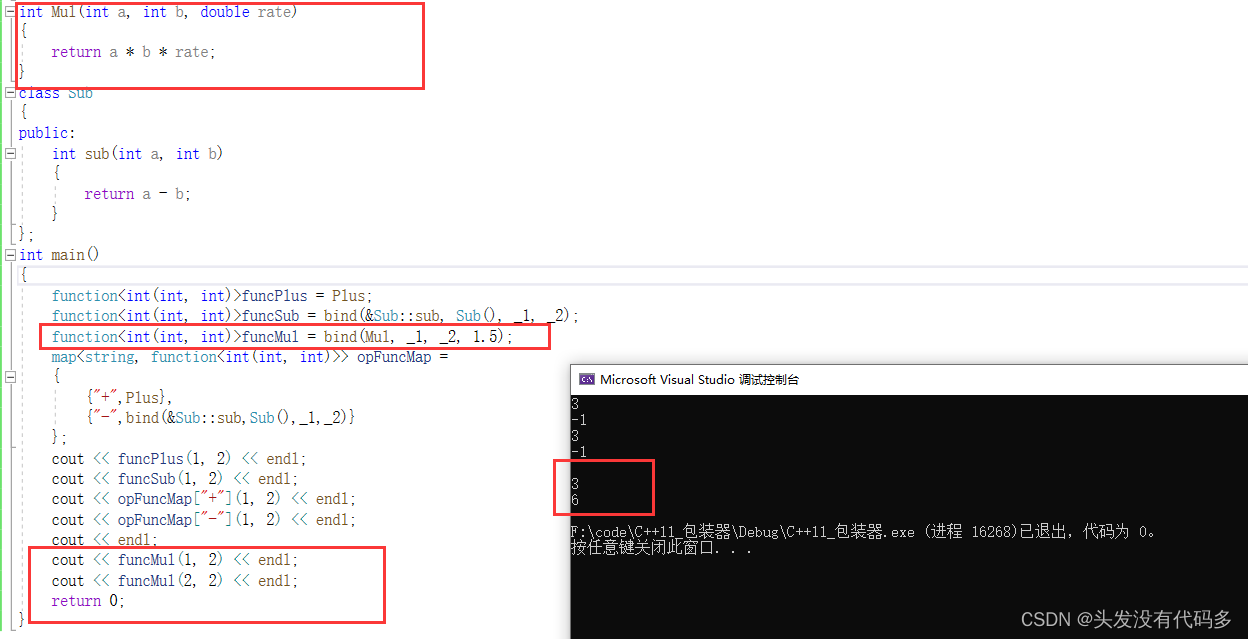
C++——C++11第三篇
目录 包装器 function包装器 bind 包装器 function包装器 function包装器 也叫作适配器。C中的function本质是一个类模板,也是一个包装器。 上面的程序验证,我们会发现useF函数模板实例化了三份。 包装器可以很好的解决上面的问题 ,让它只实…...

180 2 22222
选择题(共180题,合计180.0分) 1. 在项目开工会议期间,项目发起人告诉产品负责人和团队项目章程即将完成。然而,由于存在在紧迫的期限内满足政府监管要求的压力,发起人希望立即开始工作。产品负责人下一步应该做什么? A 告诉发起人…...

成人高考初中毕业能报名吗 需要什么条件
初中学历的人员不能直接报名成人高考,考生需要有普通高中,职业高中,中专毕业证等高中同等学力就可以进行报名,在报名期间登陆所在省的教育考试院的成人高考报名入口进行报考。成人高考报名条件是什么1、遵守宪法和法律。2、国家承…...

ChatGPT初体验
ChatGPT初体验 前言 嘿嘿,最近啊AI ChatGPT刷新各大网站,对于我们国人而将很不友好,真的太不友好了。我呢在去年open AI发布的时候就有所关注,那个时候还没有像现在这样火热。谁知道短短几个月便传遍大街小巷。 一、什么是chatG…...

ChatGPT概念狂飙!究竟魅力何在?
原文:http://www.btcwbo.com/6988.html 近期,ChatGPT引领的人工智能概念在资本市场一路狂飙,AIGC题材持续发酵。截至2月7日,Wind ChatGPT指数今年以来累计上涨超50%,汉王科技、海天瑞声、云从科技等概念股股价已经翻倍…...
如何下载阅读Spring源码-全过程详解
这篇文章记录了下载spring源码和在IDEA中打开运行的全过程,并且记录了过程中遇到的问题和解决方案,适合需要学习spring源码的同学阅读。 1.spring源码下载地址 通过Git下载spring-framework项目源码: git clone https://github.com/spring…...
学了两个月的Java,最后自己什么也不会,该怎么办?
学着学着你会发现每天的知识都在更新,也都在遗忘,可能就放弃了。但是只要自己肯练,肯敲代码,学过的知识是很容易就被捡起来的。等你学透了用不了一年也可以学好 Java的运行原理:Java是一门编译解释型语言,…...
前端vue实现获取七天时间和星期几功能
前端vue实现获取七天时间和星期几功能 功能展示代码 <div v-for"(item,index) in same_week" :class"[same_dayitem.date? activ :,dis]" click"select(item)" :keyindex><span>{{item.name}}</span><span>{{item.…...

zookeeper单机部署
一.下载zookeeper压缩包 二.上传解压安装包到/data/zookeeper目录,并解压 tar -zxvf apache-zookeeper-3.5.8-bin.tar.gz 三.修改配置文件 cd apache-zookeeper-3.5.10-bin/conf mv zoo_sample.cfg zoo.cfg vi zoo.cfg 修改为如下: dataDir/data/zooke…...

单片机输入输出模式
单片机输入输出模式输入模式模拟输入、浮空输入、上拉输入、下拉输入GPIO输出模式推挽输出、开漏输出、复用推挽输出、复用开漏输出。上下拉电阻上拉电阻下拉电阻输入模式 模拟输入、浮空输入、上拉输入、下拉输入 模拟输入:I/O端口的模拟信号(电压信号…...
数据结构_ 堆结构与堆排序(c++ 实现 + 完整代码 )
堆结构与堆排序 文章目录堆结构与堆排序引入堆堆结构所满足的数学特性准备代码----------- 往堆中插入元素----------- 删除堆顶堆排序构建完整代码及测试动态分配版本非动态版本引入堆 二叉树 具有左孩子与右孩子的最普通的二叉树。 满二叉树 特殊的二叉树:每个节…...
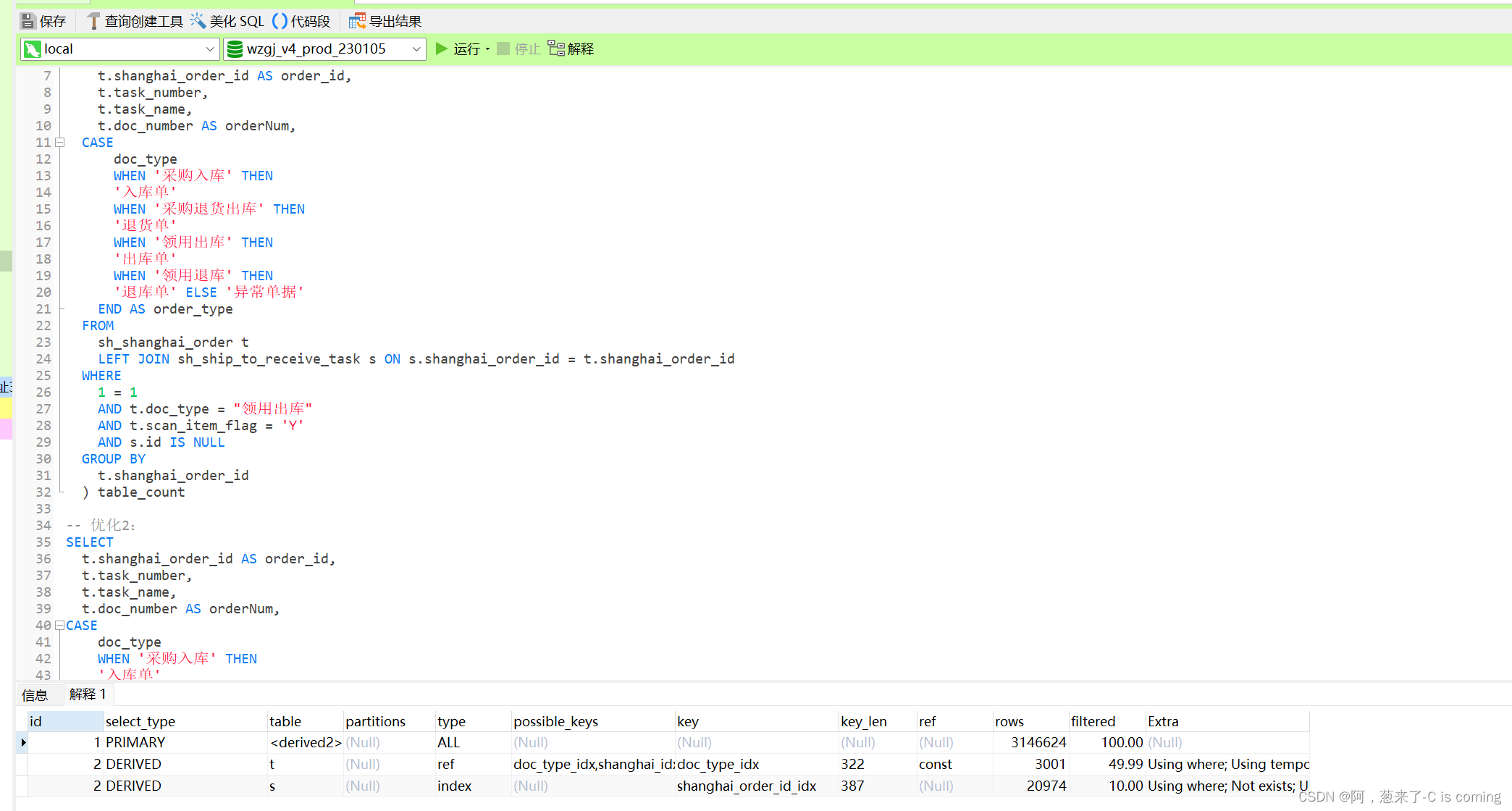
【MySQL】sql中explain解释和应用
这里写目录标题学习原因MySQL中explain的使用和用法解释explain的使用explain 运行结果的意义文字展示表格展示参考资料:结束语学习原因 在对sql的优化过程中使用了explain对指定的sql进行查看它的运行效果,以便找出sql的性能特点并进行优化 MySQL中ex…...
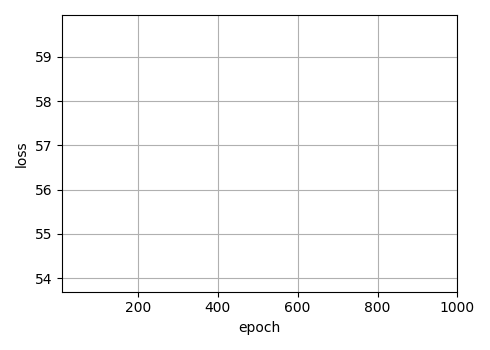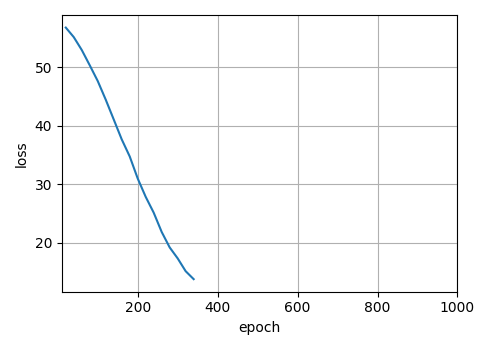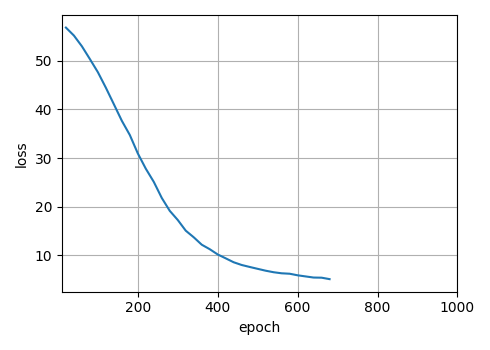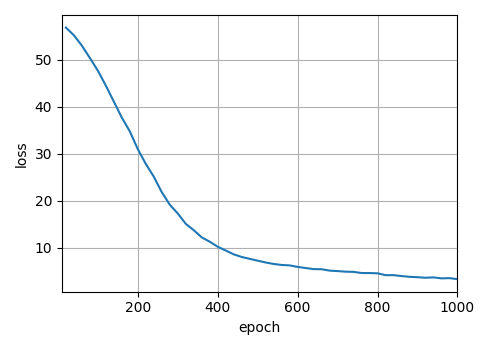
从零实现深度学习框架:Seq2Seq从理论到实战【实战篇】
来源:投稿 作者:175 编辑:学姐 往期内容: 从零实现深度学习框架1:RNN从理论到实战(理论篇) 从零实现深度学习框架2:RNN从理论到实战(实战篇) 从零实现深度…...

【数据结构入门】-链表之单链表(1)
个人主页:平行线也会相交 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【数据结构初阶(C实现)】 文章标题回顾链表链表的概念及结构各种节点打印链表尾插创建节点尾删头插头删查找在pos…...
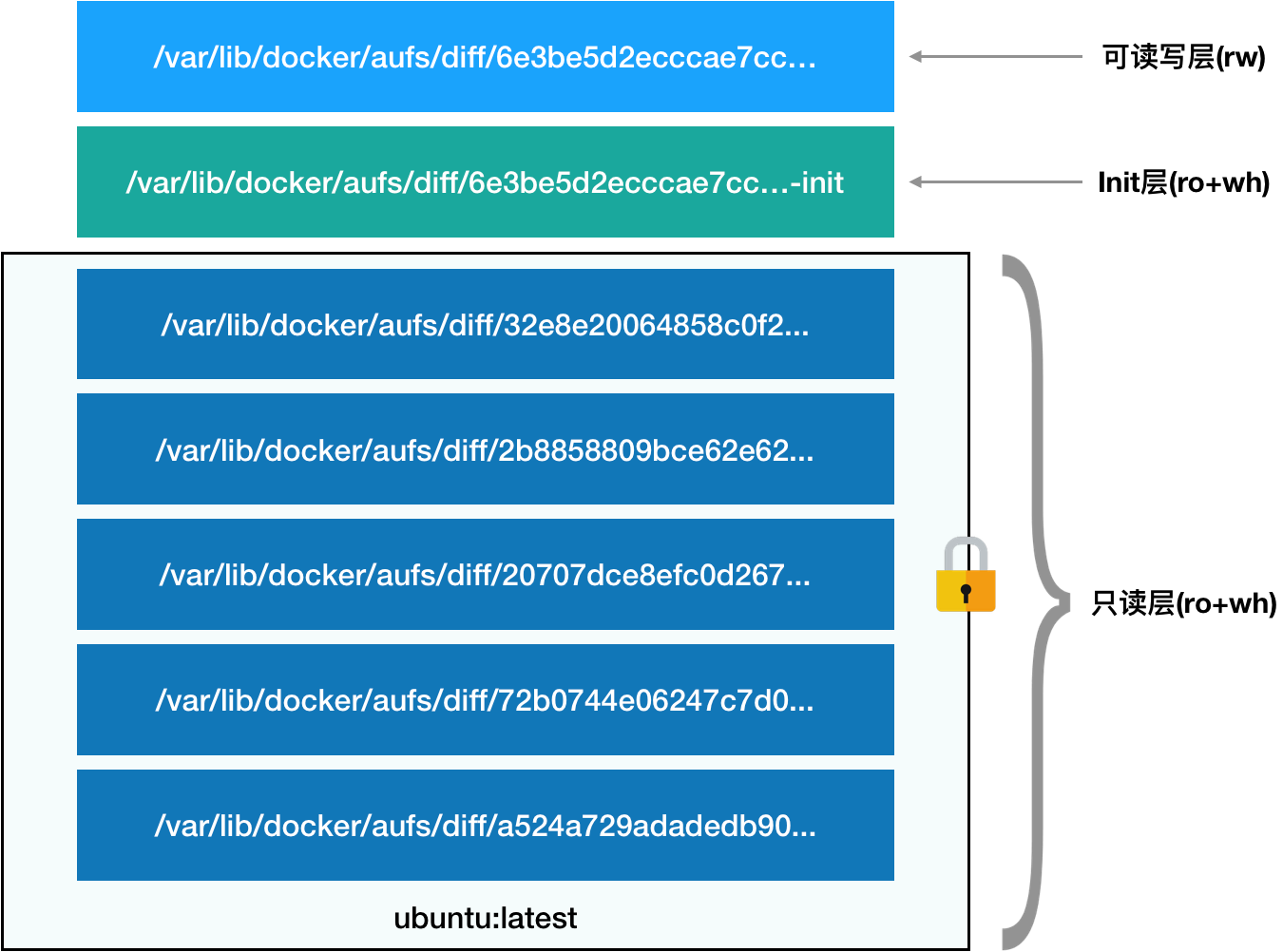
Docker竟如此简单!
文章目录什么是容器?容器隔离何为“边界”?容器和虚拟机一样吗?基于 Linux Namespace 隔离机制的弊端容器限制何为“限制”?Cgroups 对资源的限制能力缺陷单进程模型容器镜像容器的诞生容器的一致性何为“层(layer&…...
在外包干了几年,感觉自己都快费了
先说一下自己的情况。大专生,18年通过校招进入湖南某软件公司,干了接近2年的点点点,今年年上旬,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了五年的功能测试…...
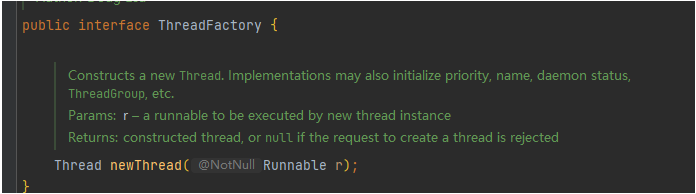
Java实现多线程有几种方式(满分回答)
目录JDK8 创建的线程的两种方式orcle文档解释方式一:继承Thread类方式二:实现Runnable接口同时用两种的情况其他间接创建方式Callable接口线程池JDK8 创建的线程的两种方式 orcle文档解释 orcle文档:https://docs.oracle.com/javase/8/docs…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
