算法通关村第十三关——幂运算问题解析
前言
幂运算为常见的数学运算,形式为 a b a^b ab ,其中a为底数,b为指数,
力扣中,幂运算相关的问题主要是判断一个数是不是特定正整数的整数次幂,以及快速幂的处理。
1.求2的幂
力扣231题,给你一个整数 n,请你判断该整数是否是 2 的幂次方。如果是,返回 true;否则,返回 false 。
分析:第一种方法是我们可以用通过逐渐缩小n值来判断是否是2的幂次方,只需要循环用除的方法就可以了,还需要判断一下n是否是正整数,如果不是就直接返回false。第二种方法是位运算,如果n是2的幂次方,那么n的二进制表示就只有一个1,如果存在非负整数 k 使得 n = 2 k n=2^k n=2k,则 n 的二进制表示为 1 后面跟 k 个0,比如n=4,其二进制表示为 ( 0100 ) 2 (0100)_2 (0100)2,n-1也就是3的二进制表示则为 ( 0011 ) 2 (0011)_2 (0011)2 ,使用位运算n & (n - 1)如果结果为0就说明n是2的幂次方,否则不是。
代码如下:
/*** 采用除法* @param n {number}* @return {boolean}* */
function isPowerOfTwo(n) {if (n <= 0) {return false;}// 这里2可以替换为任意正整数m,就是计算m的幂次方while (n % 2 === 0) {n = parseInt(n / 2);}if (n === 1) {return true;} else {return false;}
}/*** 采用位运算* @param n {number}* @return {boolean}* */function isPowerOfTwo(n) {if (n <= 0) {return false;}// 如果存在非负整数 k 使得 n=2^k,则 n 的二进制表示为 1 后面跟 k 个0return n & (n - 1) === 0;
}
拓展知识:采用循环除法的方法中,2可以替换为任意正整数m,就是计算m的幂次方。
2.求3的幂
力扣326题, 给定一个整数,写一个函数来判断它是否是 3 的幂次方。如果是,返回 true ;否则,返回 false 。整数 n 是 3 的幂次方需满足:存在整数 x 使得 n = = 3 x n == 3^x n==3x
分析:用除法思路与上题一样。这里说一下还可以用位运算的解决办法。我们知道 3 0 = 1 , 3 1 = 3 , 3 2 = 9 , . . . , 3 19 = 1162261467 3^0=1,3^1=3,3^2=9,...,3^{19}=1162261467 30=1,31=3,32=9,...,319=1162261467 ,在最大正整数范围之内,如果是3的幂就一定是1162261467的除数。
代码如下:
function isPowerOfThree(n) {if (n <= 0) {return false;}// 2^31 - 1内最大的3的幂为3^19=1162261467,只要n为1162261647的除数就说明是3的幂次方return (1162261467 % n) === 0;
}
3.求4的幂
力扣342 题,给定一个整数,写一个函数来判断它是否是 4 的幂次方。如果是,返回 true ;否则,返回 false 。整数 n 是 4 的幂次方需满足:存在整数 x 使得 n = = 4 x n == 4^x n==4x 。
分析:第一种方法还是可以用循环除法。第二种方法就是位运算,这种方法可以在求2的幂的位运算解法进一步得出, 4 k 4^k 4k其实就是 2 2 k 2^{2k} 22k ,2的偶数次幂,判断二进制表示中1的位置是否出现在从低位开始的第偶数位上即可,这里规定最低位为第0位。比如n=16,其二进制表示为 ( 00010000 ) 2 (00010000)_2 (00010000)2,1的位置为第4位。创建一个32位有符号整数 ( 10101010101010101010101010101010 ) 2 (10101010101010101010101010101010)_2 (10101010101010101010101010101010)2,让其偶数为0,奇数位为1,与n进行位与运算,如果结果为0,说明n为4的幂次方数,否则不是。为了使代码更简洁,还可以将创建的32位有符号整数用16进制表示,即 ( a a a a a a a a ) 16 (aaaaaaaa)_{16} (aaaaaaaa)16 , 也就是0xaaaaaaaa
代码如下:
function isPowerOfFour(n) {if (n <= 0) {return false;}return (n & (n - 1)) === 0 && (n & 0xaaaaaaaa) === 0;
}
相关文章:

算法通关村第十三关——幂运算问题解析
前言 幂运算为常见的数学运算,形式为 a b a^b ab ,其中a为底数,b为指数, 力扣中,幂运算相关的问题主要是判断一个数是不是特定正整数的整数次幂,以及快速幂的处理。 1.求2的幂 力扣231题,给…...

Python 之使用Numpy库来加载Numpy(.npy)文件并检查其内容
文章目录 总的介绍data.dtypedata.shapedata.ndimdata.size 总的介绍 要判断一个Numpy(.npy)文件的数据集类型,你可以使用Python中的Numpy库来加载该文件并检查其内容。以下是一些常见的步骤: 导入Numpy库: 首先&…...

C#学习系列之UDP同端口收发问题
C#学习系列之UDP同端口收发问题 前言解决办法关于JoinMulticastGroup总结 前言 想测试自己的程序问题,建立了两个UDP程序,一个往端口中接到数就传出去,另一个从这个端口接数据来解析。 出现的问题是 每次打开端口,另一个程序就无…...

SpringMVC之文件上传下载以及jrebel的使用
目录 一、文件上传 1.1 导入依赖 1.2 配置文件上传解析器 1.3 配置服务器存放文件地址 1.3.1 点击编辑Configurations 1.3.2 将项目部署至tomcat服务器上 1.3.3 配置相对路径 1.4 导入PropertiesUtil工具类 1.5 编写resource.properties 1.6 添加sql 1.7 编写PageCo…...

基于Fomantic UI Web构建 个人导航站点网站源码 网站技术导航源码
BYR-Navi-master好看有个性的网站技术导航源码 该网站基于Fomantic UI Web框架构建,整个项目的设计和构建具有高度的配置和定制灵活性。 整体风格比较适合个人导航站点使用 搜索框输入关键词后,点击上方搜索引擎图标可跳转打开对应搜索引擎搜索结果&am…...

DRF02-请求响应与路由
文章目录 1. http请求响应1.1. 请求与响应1.1.1 Request1.1.1.1 常用属性1).data2).query_params3)request._request基本使用1.1.2 Response1.1.2.1 构造方式1.1.2.2 response对象的属性1).data2).status_code3).content1.1.2.3 状态码1)信息告知 - 1xx2)成功 - 2xx3)…...

http直接调用paddlepaddle实现文字转语音,语音转文字
由于环境问题,折腾好久,记录下来,安装后使用还是很方便的 记录下来,方便自己,方便大家 1.安装 参考官方文档: mirrors / paddlepaddle / paddlespeech GitCode 2.启动server 参考官方文档: mirrors / paddlepaddle / paddlespeech GitCode 3.直接调用 参考官方文档: htt…...
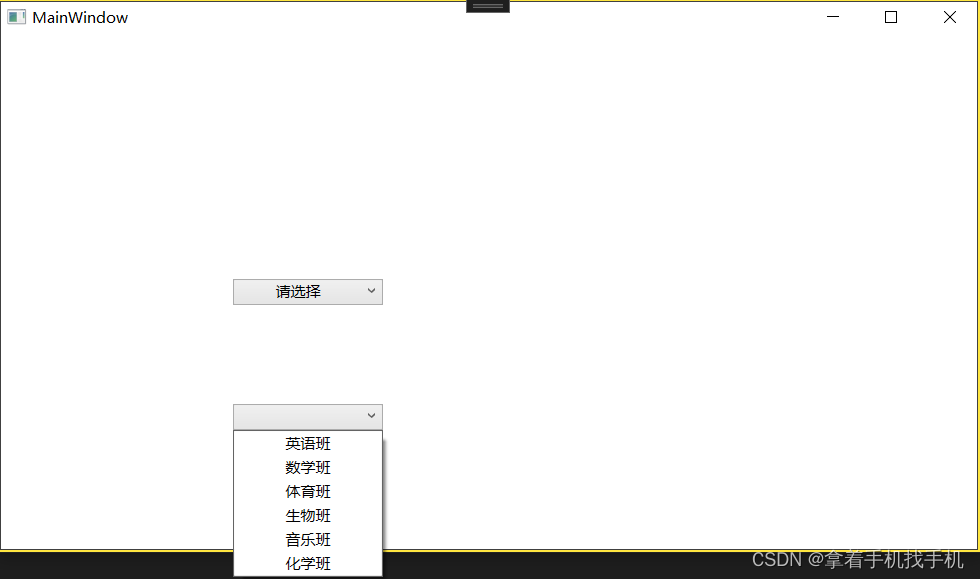
9. xaml ComboBox控件
1.运行图像 2.运行源码 a.Xaml源码 <Grid Name="Grid1"><!--IsDropDownOpen="True" 默认就是打开的--><ComboBox x:Name="co...
:密钥封装 KEM(附源码分析))
【后量子密码】CRYSTALS-KYBER 算法(二):密钥封装 KEM(附源码分析)
一、前言 Kyber 算法是一种满足 IND-CCA2 安全的密钥封装机制(key-encapsulation mechanism,KEM),其安全性依赖于MLWE 问题的困难性。Kyber 算法构建采用了两阶段的方法:首先引入了一种IND-CPA 安全的公钥加密方案,用于加密长度为32字节的消息,称之为Kyber.CPAPKE;然后…...

什么是原⼦操作?在 JUC 中有哪些原⼦类?
原子操作是一种在多线程环境下不会被中断的操作,它要么完全执行,要么完全不执行,不会出现中间状态。原子操作通常是对共享数据的操作,确保多个线程同时访问共享数据时不会导致数据不一致或损坏。 在Java中,java.util.concurrent 包提供了一组原子类,用于执行原子操作。以…...

2022年12月 C/C++(八级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C++编程(1~8级)全部真题・点这里 第1题:生理周期 人生来就有三个生理周期,分别为体力、感情和智力周期,它们的周期长度为23天、28天和33天。每一个周期中有一天是高峰。在高峰这天,人会在相应的方面表现出色。例如,智力周期的高峰,人会思维敏捷,精力容易高度集中。因…...

Hadoop的HDFS的集群安装部署
注意:主机名不要有/_等特殊的字符,不然后面会出问题。有问题可以看看第5点(问题)。 1、下载 1.1、去官网,点下载 下载地址:https://hadoop.apache.org/ 1.2、选择下载的版本 1.2.1、最新版 1.2.2、其…...
uniapp 在 onLoad 事件中 this.$refs 娶不到的问题
现象 本人想在主页面加载的时候调用子组件的方法。示例代码如下: 运行,发现 this.$refs 取不到。如下图所示: 解决方法,把onLoad 换为 onReady 就可以了。...

常見算法時間複雜度分析
当我们进行算法分析时,通常会忽略掉常数倍数的因子和低阶项,只考虑最高阶的项。这是因为在大规模问题下,较小的项和常数倍数的因子相对于最高阶的项来说变得可以忽略不计。 以下是一些常见的示例,说明了常数倍数的因子和高阶项对…...

自学Python05-学会Python中的函数定义
亲爱的同学们,今天我们将开始学习 Python 中的函数。函数就像一个魔法盒子,可以让我们在程序中执行一段代码,并且可以反复使用。这样,我们的程序就可以变得更加简洁和易于理解。现在,让我们一起来学习如何使用函数吧&a…...
)
设计模式-组合模式(Composite)
文章目录 前言一、组合模式的概念二、组合模式的优缺点1.优点2.缺点 三、组合模式的实现总结 前言 组合模式(Composite Pattern)是一种结构型设计模式,它允许你将对象组合成树状结构以表示“整体-部分”的层次结构。组合模式使得客户端可以统…...

架构核心技术之微服务架构
小熊学Java:https://www.javaxiaobear.cn/,文末有免费资源 本文我们来学习微服务的架构设计 主要包括如下内容。 单体系统的困难:编译部署困难、数据库连接耗尽、服务复用困难、新增业务困难。 微服务框架:Dubbo 和 Spring Clou…...
SQL Server2022版+SSMS安装教程(保姆级)
SQL Server2022版SSMS安装教程(保姆级) 一,安装SQL Server数据库 1.下载安装包 (1)百度网盘下载安装包 链接:https://pan.baidu.com/s/1A-WRVES4EGv8EVArGNF2QQ?pwd6uvs 提取码:6uvs &…...
go语言基础---8
Http请求报文格式分析 package mainimport ("fmt""net" )func main() {//监听listener, err : net.Listen("tcp", ":8000")if err ! nil {fmt.Println("listener err", err)return}defer listener.Close()//阻塞等待用户的…...

Oracle的 dblink 学习笔记
文章目录 一、基础环境二、适用场景三、过程和方法四、参考资料 版权声明:本文为CSDN博主「杨群」的原创文章,遵循 CC 4.0 BY-SA版权协议,于2023年9月10日首发于CSDN,转载请附上原文出处链接及本声明。 原文链接:http…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...
