2023牛客暑假多校第四场(补题向题解:J)
终于有时间来慢慢补补题了
J Qu’est-ce Que C’est?
作为队内的dp手,赛时想了好久,等学弟学妹都出了还是不会,羞愧,还好最终队友做出来了。
链接J Qu’est-ce Que C’est?
题意
长度为 n n n 的数组 a a a,每个数的取值范围 a i = [ − m , m ] a_i = [-m, m] ai=[−m,m],问所有满足长度 > 1 >1 >1 的子段的和为非负数的数组可能的数量。 1 ≤ n , m ≤ 5000 1\leq n,m\leq 5000 1≤n,m≤5000。
思路
看了懵哥的题解,看到状态定义后就会了,我怎么就想不到呢?
法一
dp状态定义 f [ i ] [ j ] : f[i][j]: f[i][j]: 前 i i i 个数,最小后缀和为 j j j 的方案数 j = [ − 5000 , 5000 ] j = [-5000, 5000] j=[−5000,5000]。因为是最小后缀和,那么如果有后缀 < − 5000 <-5000 <−5000 的说明至少是两个数以上的和为负数,与题意不符是不合法的方案,所以数组大小开到 [ 0 , 10000 ] [0,10000] [0,10000] 即可(离散化后)。
我们先不管时间复杂度,根据dp定义先敲个状态转移出来,代码如下:
#include <bits/stdc++.h>
using namespace std;#define ll long longconst int N = 5010, mod = 998244353;int f[N][N * 2]; // 前i个数,最小后缀和为j的方案数 j = [-5000, 5000]void add(int& a, int b){a = (a + b) % mod;
}
int main(){int n, m;cin >> n >> m;f[0][2 * m] = 1;for(int i = 1; i <= n; i ++){for(int j = -m; j <= m; j ++){ // 枚举最小后缀for(int k = m; k >= -m; k --){ // 枚举当前a_i选哪个数if(j + k < 0) break;add(f[i][min(j + k, k) + m], f[i - 1][j + m]);}}}int ans = 0;for(int i = -m; i <= m; i ++){add(ans, f[n][i + m]);}cout << ans;return 0;
}时间复杂度为 O ( n 3 ) O(n^3) O(n3),我们观察一下代码如何优化,发现会有大量连续的 k k k, f [ i ] [ min ( j + k , k ) ] f[i][\min(j + k, k)] f[i][min(j+k,k)] 加的是同一个状态 f [ i − 1 ] [ j ] f[i - 1][j] f[i−1][j]。那么经典优化方案不就来了吗,差分前缀和优化。
以下分情况讨论:
因为是 min ( j + k , k ) \min(j + k, k) min(j+k,k)
- j j j 是非正数
无论当前 k k k 选什么, j + k ≤ k j + k \leq k j+k≤k,所以状态一定是转移到 j + k j + k j+k,所以对于一个非正数的 j j j 可转移的范围就是 0 ∼ j + m 0 \sim j + m 0∼j+m。
// 区间 [l, r] + val f_l + val f_{r + 1} + val
for(int j = -m; j <= 0; j ++){f[i][m] = (f[i][m] + f[i - 1][j + m]) % mod;// 差分 +f[i][m + j + m + 1] = (f[i][m + j + m + 1] + mod - f[i - 1][j + m]) % mod;// 差分 -
}
- j j j 是正数
同理无论当前 k k k 选什么, k ≤ j + k k \leq j + k k≤j+k,所以状态一定是转移到 k k k,所以对于一个正数 j j j,可以转移的范围就是 − j ∼ m -j\sim m −j∼m。
for(int j = 1; j <= m; j ++){f[i][-j + m] = (f[i][-j + m] + f[i - 1][j + m]) % mod;f[i][m + m + 1] = (f[i][m + m + 1] + mod - f[i - 1][j + m]) % mod;
}
完整代码
#include <bits/stdc++.h>
using namespace std;#define ll long longconst int N = 5010, mod = 998244353;int f[N][N * 2]; // 前i个数,最小后缀和为j的方案数 j = [-5000, 5000]void add(int& a, int b){a = (a + b) % mod;
}
int main(){int n, m;cin >> n >> m;f[0][2 * m] = 1;for(int i = 1; i <= n; i ++){/*for(int j = -m; j <= m; j ++){for(int k = m; k >= -m; k --){if(j + k < 0) break;add(f[i][min(j + k, k) + m], f[i - 1][j + m]);}}*/// 考虑差分前缀和优化// j 是 负数 k 是正数 f[i][j + k + m] 从0 ~ m + j// j 是 正数 k 是负数/正数 f[i][k + m] 从-j ~ mfor(int j = -m; j <= 0; j ++){f[i][m] = (f[i][m] + f[i - 1][j + m]) % mod; // 差分 +f[i][m + j + m + 1] = (f[i][m + j + m + 1] + mod - f[i - 1][j + m]) % mod; // 差分 -}for(int j = 1; j <= m; j ++){f[i][-j + m] = (f[i][-j + m] + f[i - 1][j + m]) % mod;f[i][m + m + 1] = (f[i][m + m + 1] + mod - f[i - 1][j + m]) % mod;}for(int j = -m + 1; j <= m; j ++){ // 前缀和f[i][j + m] = (f[i][j + m] + f[i][j + m - 1]) % mod;}}int ans = 0;for(int i = -m; i <= m; i ++){add(ans, f[n][i + m]);}cout << ans;return 0;
}相关文章:
)
2023牛客暑假多校第四场(补题向题解:J)
终于有时间来慢慢补补题了 J Qu’est-ce Que C’est? 作为队内的dp手,赛时想了好久,等学弟学妹都出了还是不会,羞愧,还好最终队友做出来了。 链接J Qu’est-ce Que C’est? 题意 长度为 n n n 的数组 a a a,每…...

第 362 场 LeetCode 周赛题解
A 与车相交的点 数据范围小直接暴力枚举 class Solution { public:int numberOfPoints(vector <vector<int>> &nums) {unordered_set<int> vis;for (auto &p: nums)for (int i p[0]; i < p[1]; i)vis.insert(i);return vis.size();} };B 判断能否…...
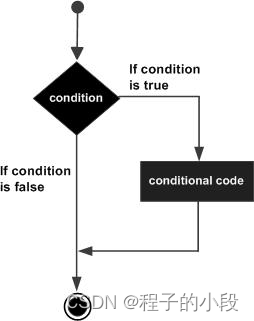
C++ if 语句
一个 if 语句 由一个布尔表达式后跟一个或多个语句组成。 语法 C 中 if 语句的语法: if(boolean_expression) {// 如果布尔表达式为真将执行的语句 }如果布尔表达式为 true,则 if 语句内的代码块将被执行。如果布尔表达式为 false,则 if 语…...
业务安全及实战案例
业务安全 关于漏洞: 注入业务逻辑信息泄露 A04:2021 – Insecure Design 在线靶场PortSwigger 1. 概述 1.1 业务安全现状 1.1.1 业务逻辑漏洞 近年来,随着信息化技术的迅速发展和全球一体化进程的不断加快,计算机和网络已经成为与…...

十一)Stable Diffussion使用教程:人物三视图
现在我们通过一个个具体的案例,去进阶SD的使用。 本篇案例:绘制Q版人物三视图 1)我们先选择一个偏3D的模型,选择文生图,输入魔法; 2)然后选择触发三视图的Lora:<lora:charturnerbetaLora_charturnbetalora:0.6>,注意这里的名称都是本地重新命名的,非原来C站下…...

超级等级福利礼包
文章目录 一、 介绍二、 设计等级礼包的目的1. 提升游戏玩家活跃度2. 提升游戏用户吸引力3. 提高游戏用户留存率4. 实现间接收入5. 持续营收 三、 玩家心理总结四、总结该模式的赢利点五、 该模式的应用场景举例 一、 介绍 超级等级福利礼包,玩家每升级5级即可获得…...

如何用Jmeter提取和引用Token
1.执行获取token接口 在结果树这里,使用$符号提取token值。 $根节点,$.data.token表示提取根节点下的data节点下的token节点的值。 2.使用json提取器,提取token 变量路径就是把在结果树提取的路径写上。 3.使用BeanShell取样器或者BeanShell后…...

C#文件拷贝工具
目录 工具介绍 工具背景 4个文件介绍 CopyTheSpecifiedSuffixFiles.exe.config DataSave.txt 拷贝的存储方式 文件夹介绍 源文件夹 目标文件夹 结果 使用 *.mp4 使用 *.* 重名时坚持拷贝 可能的报错 C#代码如下 Form1.cs Form1.cs设计 APP.config Program.c…...

Redis——Java中的客户端和API
Java客户端 在大多数的业务实现中,我们还是使用编码去操作Redis,对于命令的学习只是知道这些数据库可以做什么操作,以及在后面学习到了Java的API之后知道什么方法对应什么命令即可。 官方推荐的Java的客户端网页链接如下: 爪哇…...
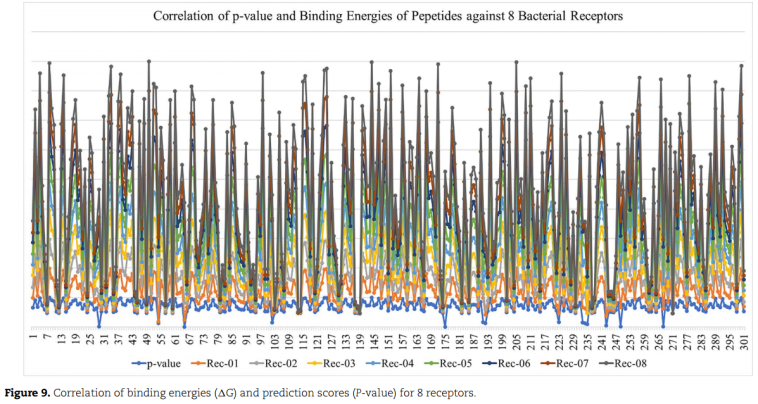
Brief. Bioinformatics2021 | sAMP-PFPDeep+:利用三种不同的序列编码和深度神经网络预测短抗菌肽
文章标题:sAMP-PFPDeep: Improving accuracy of short antimicrobial peptides prediction using three different sequence encodings and deep neural networks 代码:https://github.com/WaqarHusain/sAMP-PFPDeep 一、问题 短抗菌肽(sAMPs)&#x…...

问道管理:华为产业链股再度拉升,捷荣技术6连板,华力创通3日大涨近70%
华为产业链股6日盘中再度拉升,到发稿,捷荣技能涨停斩获6连板,华映科技亦涨停收成3连板,华力创通大涨超19%,蓝箭电子涨约11%,力源信息涨超4%。 捷荣技能盘中再度涨停,近7日已累计大涨超90%。公司…...
面试设计模式-责任链模式
一 责任链模式 1.1 概述 在进行请假申请,财务报销申请,需要走部门领导审批,技术总监审批,大领导审批等判断环节。存在请求方和接收方耦合性太强,代码会比较臃肿,不利于扩展和维护。 1.2 责任链模式 针对…...
Qt 开发 CMake工程
Qt 入门实战教程(目录) 为何要写这篇文章 目前CMake作为C/C工程的构建方式在开源社区已经成为主流。 企业中也是能用CMake的尽量在用。 Windows 环境下的VC工程都是能不用就不用。 但是,这个过程是非常缓慢的,所以࿰…...
2.k8s账号密码登录设置
文章目录 前言一、启动脚本二、配置账号密码登录2.1.在hadoop1,也就是集群主节点2.2.在master的apiserver启动文件添加一行配置2.3 绑定admin2.4 修改recommended.yaml2.5 重启dashboard2.6 登录dashboard 总结 前言 前面已经搭建好了k8s集群,现在设置下…...

【代表团坐车】Python 实现-附ChatGPT解析
1.题目 某组织举行会议,来了多个代表团同时到达,接待处只有一辆汽车,可以同时接待多个代表团,为了提高车辆利用率,请帮接待员计算可以坐满车的接待方案,输出方案数量。 约束: 1.一个团只能上一辆车,并且代表团人数(代表团数量小于30,每人代表团人数小于30)小于汽车容量…...

【Java】x-easypdf: 一种简单易用的PDF处理库
引言 在处理和生成PDF文档时,有许多库可供选择。其中,x-easypdf是一种简单易用的PDF处理库,可以帮助开发人员轻松地创建、编辑和操作PDF文档。本文将介绍x-easypdf的基本概念、安装方法、主要功能以及使用示例。 安装x-easypdf 要使用x-ea…...

1 Linux输入子系统
1 Linux输入子系统 https://www.cnblogs.com/beijiqie1104/p/11418082.html Linux input 子系统详解 https://www.cnblogs.com/yikoulinux/p/15208238.html...
Zabbix 利用 Grafana 进行图形展示
安装grafana和插件 配置zabbix数据源 导入模版 查看数据 1.安装grafana wget https://mirrors.tuna.tsinghua.edu.cn/grafana/yum/rpm/Packages/grafana-10.0.0-1.x86_64.rpm [rootrocky8 apps]# yum install grafana-10.0.0-1.x86_64.rpm [rootrocky8 apps]# systemctl sta…...

【LeetCode周赛】LeetCode第362场周赛
LeetCode第362场周赛 与车相交的点判断能否在给定时间到达单元格将石头分散到网格图的最少移动次数 与车相交的点 给你一个下标从 0 开始的二维整数数组 nums 表示汽车停放在数轴上的坐标。对于任意下标 i,nums[i] [starti, endi] ,其中 starti 是第 i…...

Leetcode128. 最长连续序列
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 题解&#…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...
