LeetCode 36. 有效的数独
LeetCode 36. 有效的数独
难度:middle\color{orange}{middle}middle
题目描述
请你判断一个 9x99 x 99x9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
- 数字 1−91-91−9 在每一行只能出现一次。
- 数字 1−91-91−9 在每一列只能出现一次。
- 数字 1−91-91−9 在每一个以粗实线分隔的 3x33x33x3 宫内只能出现一次。(请参考示例图)
注意:
- 一个有效的数独(部分已被填充)不一定是可解的。
- 只需要根据以上规则,验证已经填入的数字是否有效即可。
- 空白格用 ′.′'.'′.′ 表示。
示例 1:

输入:board =
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出:true
示例 2:
输入:board =
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出:false
解释:除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
提示:
- board.length==9board.length == 9board.length==9
- board[i].length==9board[i].length == 9board[i].length==9
- board[i][j]board[i][j]board[i][j] 是一位数字(1−91-91−9)或者 ′.′'.'′.′
算法
(暴力枚举)
- 判断每一行是否存在相同的数字。
- 判断每一列是否存在相同的数字。
- 判断每一个单独的小方格是否存在相同的数字。
复杂度分析
-
时间复杂度:O(1)O(1)O(1),数独共有 81 个单元格,只需要对每个单元格遍历即可。
-
空间复杂度 : O(1)O(1)O(1),只需要一个判重数组即可。
C++ 代码
class Solution {
public:bool isValidSudoku(vector<vector<char>>& board) {bool st[9];//判断行for (int i = 0; i < 9; i ++) {memset(st, 0, sizeof st);for (int j = 0; j < 9; j ++) {if (board[i][j] != '.') {int t = board[i][j] - '1';if (st[t]) return false;st[t] = true;}}}//判断列for (int i = 0; i < 9; i ++) {memset(st, 0, sizeof st);for (int j = 0; j < 9; j ++) {if (board[j][i] != '.') {int t = board[j][i] - '1';if (st[t]) return false;st[t] = true;}}}//判断小方格for (int i = 0; i < 9; i += 3) {for (int j = 0; j < 9; j += 3) {memset(st, 0, sizeof st);for (int x = 0; x < 3; x ++) {for (int y = 0; y < 3; y ++) {if (board[i + x][j + y] != '.') {int t = board[i + x][j + y] - '1';if (st[t]) return false;st[t] = true;}}}}}return true;}
};
相关文章:

LeetCode 36. 有效的数独
LeetCode 36. 有效的数独 难度:middle\color{orange}{middle}middle 题目描述 请你判断一个 9x99 x 99x9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。 数字 1−91-91−9 在每一行只能出现一次。数字 1−91-91−9 在每一列…...

2023-02-22 cascades-columbia-核心处理记录
摘要: columbia是哥伦比亚对于cascades的一个改进, 并且paper写的也相对详尽. 虽然cacades的实现有很多,比较出名的就是greenplum的gporca, 不过columbia也有其显著的优点. 本文通过对columbia的分析展开对cascades优化器思想的探讨. 参考: 2023-02-10 哥伦比亚cascades-xu-…...
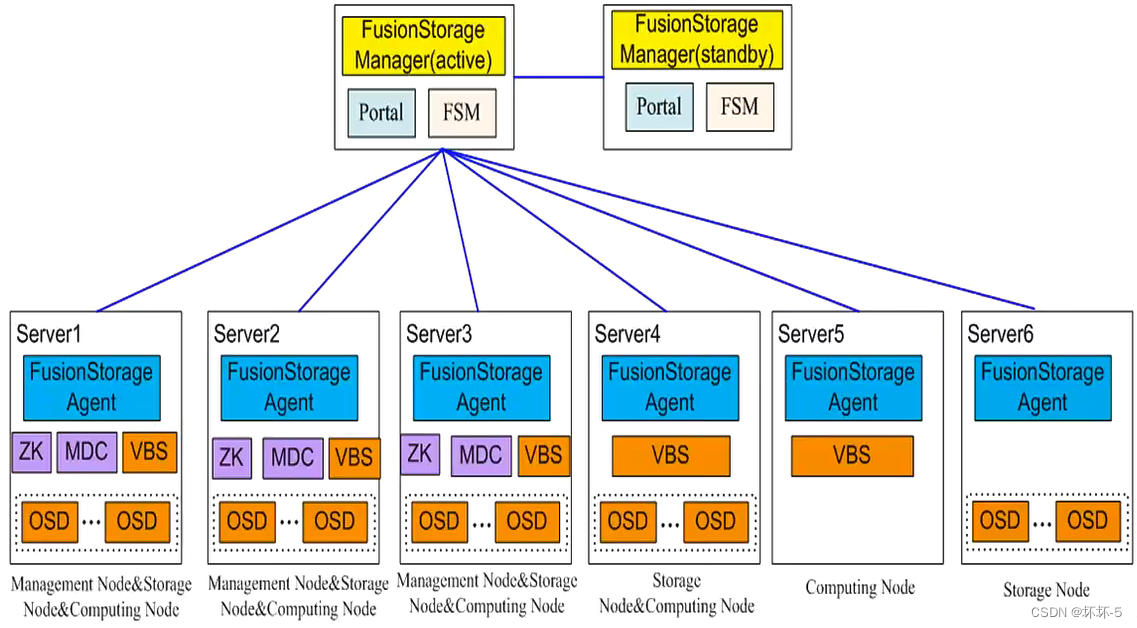
华为分布式存储(FusionStorage)
Server SAN SAN:存储区域网络 IP SAN:以太网交换机和普通网线连接的存储,交换机之间做堆叠FC SAN:FC(光纤)交换机和光纤连接的存储,交换机之间做级联Server SAN:可以使用以太网交换机…...

说说 React 中 fiber、DOM、ReactElement、实例对象之间的引用关系
原生组件 fiber 原生组件 fiber,指的就是 type 为 “span”、“div” 的 fiber。 1.fiber.stateNode 指向真实 DOM 节点;2.node["__reactFiber$" randomKey] 指向对应 fiber,使用随机数是防止和业务代码的属性名冲突,…...
)
LaTex公式使用(Word中的公式编辑,尤其是方程组等联合公式)
文章目录 LaTex公式使用(Word中的公式编辑,尤其是方程组等联合公式)refnotedemoLaTex公式使用(Word中的公式编辑,尤其是方程组等联合公式) ref markdown中公式编辑教程 在 Microsoft Word 中使用 LaTeX 输入数学公式【比较全,介绍了支持的语法和不支持的语法】 用wo…...
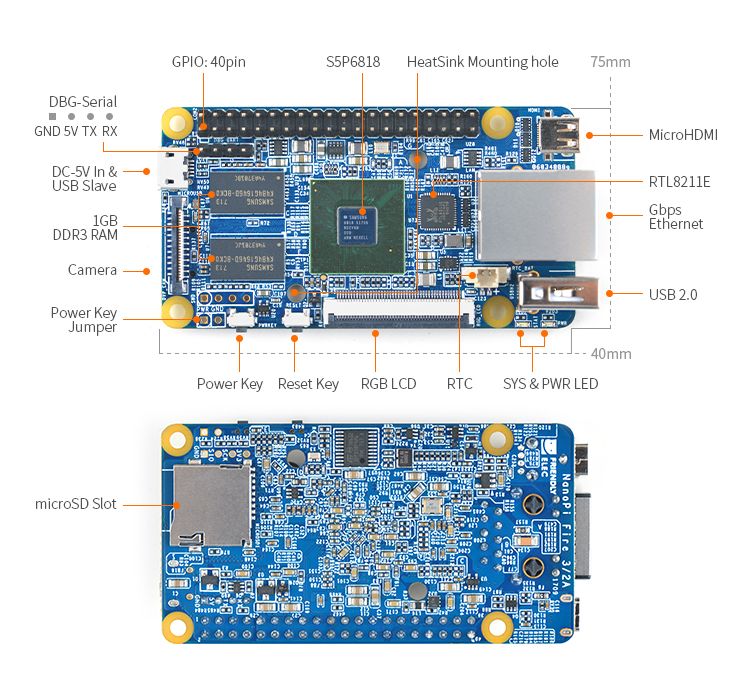
S5P6818_系统篇(2)源码编译及烧录
源码获取 源码获取和操作流程 1.下载liunux下的系统制作脚本,可以烧录系统和构建镜像 git clone https://github.com/friendlyarm/sd-fuse_s5p6818.git 如果出现git错误可使用如下方法: git config --global http.sslverify false 2.阅读该工具rea…...
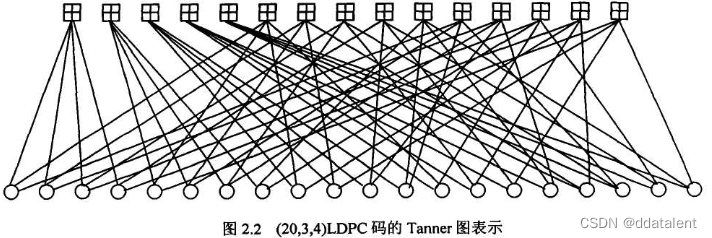
LDPC码的编译码原理简述
关于fpga调用ldpc IP core的相关参数问题可以看我的另一篇文章 LDPC码由Gallager在1962年提出,全称为 Low Density Parity-check Codes 低密度奇偶校验码 它的译码性能可以逼近Shannon信道容量限,广富盛名的Turbo码也被证明是LDPC码的一个特例。并且LDPC…...

网络安全——数链路层据安全协议
作者简介:一名云计算网络运维人员、每天分享网络与运维的技术与干货。 座右铭:低头赶路,敬事如仪 个人主页:网络豆的主页 目录 前言 一.数据链路层安全协议简介 1.数据链路安全性 二.局域网数据链路层协议 1.…...
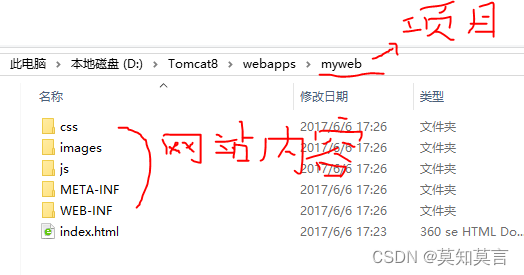
spring的启动过程(一) :IOC容器的启动过程
一、web容器的加载 首先我们要先知道一个web项目的启动过程。 将Web项目部署到Tomcat中的方法之一,是部署没有封装到WAR文件中的Web项目。要使用这一方法部署未打包的webapp目录,只要把我们的项目(编译好的发布项目,非开发项目&am…...
这次,我的CentOS又ping不通www.baidu.com了(gateway配置)
当我们保证了宿主机与虚拟机的ip地址在同一网段,并且我们使用虚拟机ping宿主机,与宿主机ping虚拟机都可以互相ping通的情况下虚拟机却ping不通外网了,由于涉及到了跨越网络访问,所以我们应该把问题聚焦在网关的配置上!…...

启智社区“我为开源狂”第六期活动小白教程之基础活跃榜
一、写在前面 春天来啦~启智社区第六期活动也来啦! 有奖金的哦~~ 基础活跃榜奖金根据用户活跃程度进行100-300元的激励。 挑战升级榜需要用户完成相应任务,达标者可获得300-1000元的激励。 邀请助力榜根据用户邀请情况进行积分累加,按实际达…...

华为OD机试 - 区块链文件转储系统(Python)【2023-Q1 新题】
华为OD机试300题大纲 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 华为OD详细说明:https://dream.blog.csdn.net/article/details/128980730 区块链文件转储系…...

【字节面试】Fail-fast知识点相关知识点
字节面试,问到的一个小知识点,这里做一下总结,其实小编之前有一篇文章,已经对此有过涉及,不过这里知识专项针对于问题,把这个知识点拎出来说一下。 1.问题 什么是Fail-fast机制? Hashmap是否拥…...
git应用笔记(三)
在新增虚拟机linux的基础上,做git的下载与提交 1、初始化自己的用户名和邮箱。 git config --global user.name “输入你的用户名” git config --global user.email “输入你的邮箱” 2、将本地公钥及配置如图1复制粘贴到虚拟机当前用户.ssh\目录下 4929a0205f43…...
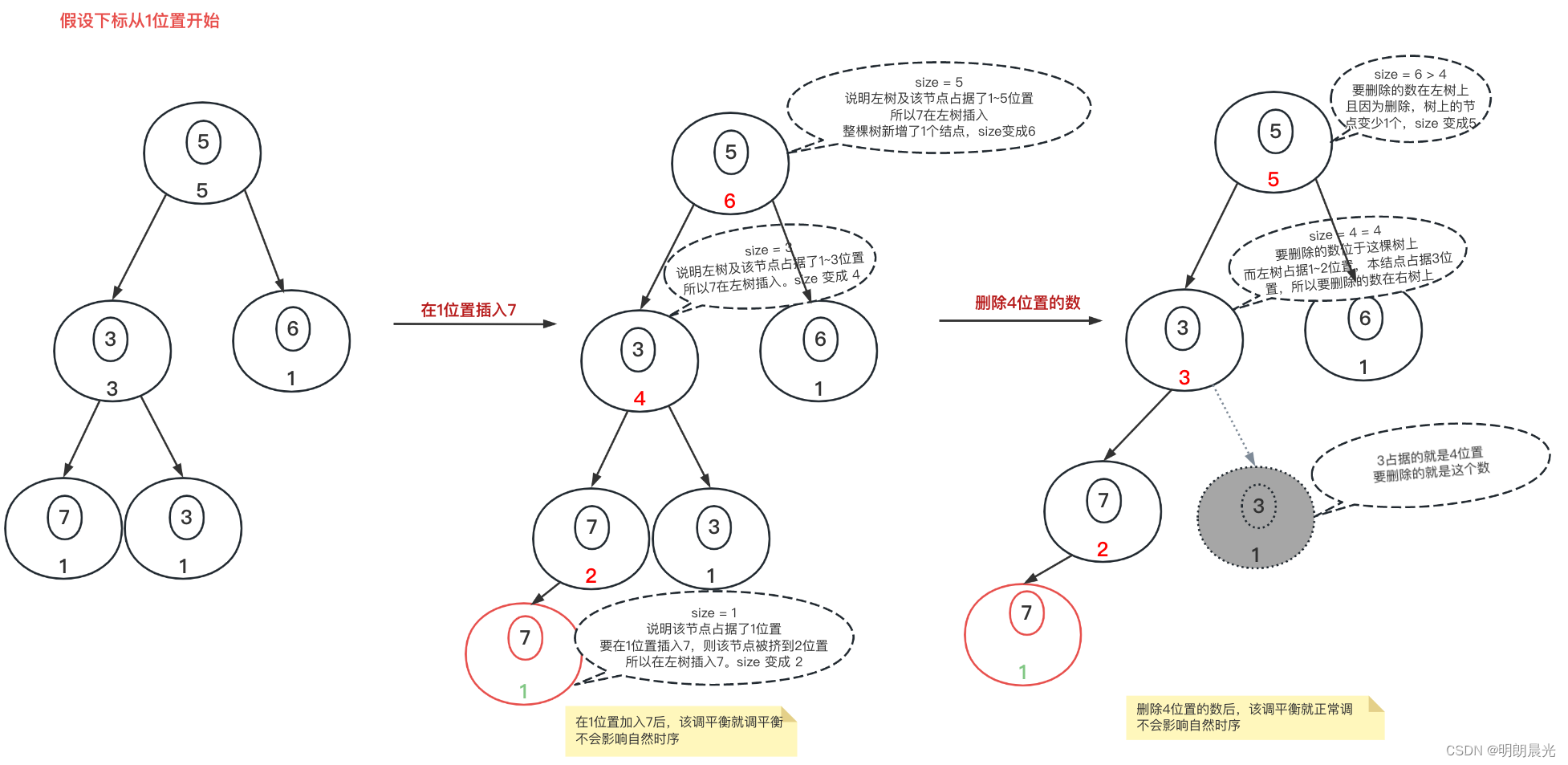
有序表的应用:设计一个增、删、查数据的时间复杂度均为O(logN)的结构
1、题目描述 设计一个结构包含如下三个方法: void add(int index, int num); //把num加入到index位置 int get(int index); //取出index位置的值(是自然序的index位置,非排序后) void remove(int index); //把index位置上的值删…...

离线环境拷贝迁移 conda envs 环境(蛮力方法,3行命令)
前言 最近要使用 GPU 服务器做实验,可惜的是,有网络连接的服务器显卡旧,算力不够;显卡较新的机器没有联网。于是有需求将旧机器上配置好的 conda 环境迁移至新机器。网上给的默认方法生成 yaml 文件迁移等 需要联网,只…...
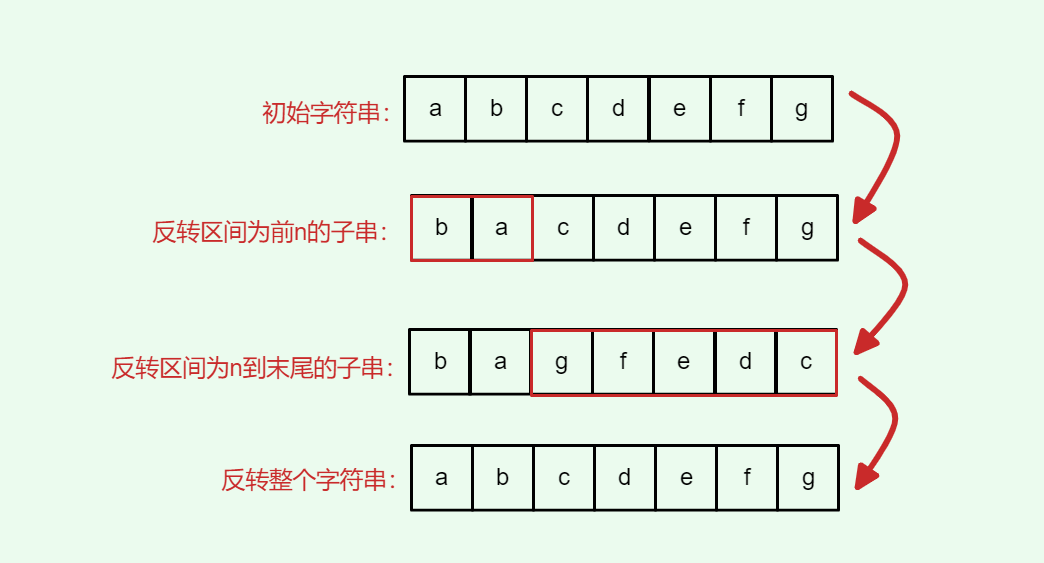
【数据结构与算法】字符串1:反转字符串I 反转字符串II 反转字符串里的单词 剑指offer(替换空格、左旋转字符串)
今日任务 344.反转字符串541.反转字符串II剑指Offer 05.替换空格151.反转字符串里的单词剑指Offer58-II.左旋转字符串 1.Leetcode344.反转字符串 来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/reverse-string &#…...
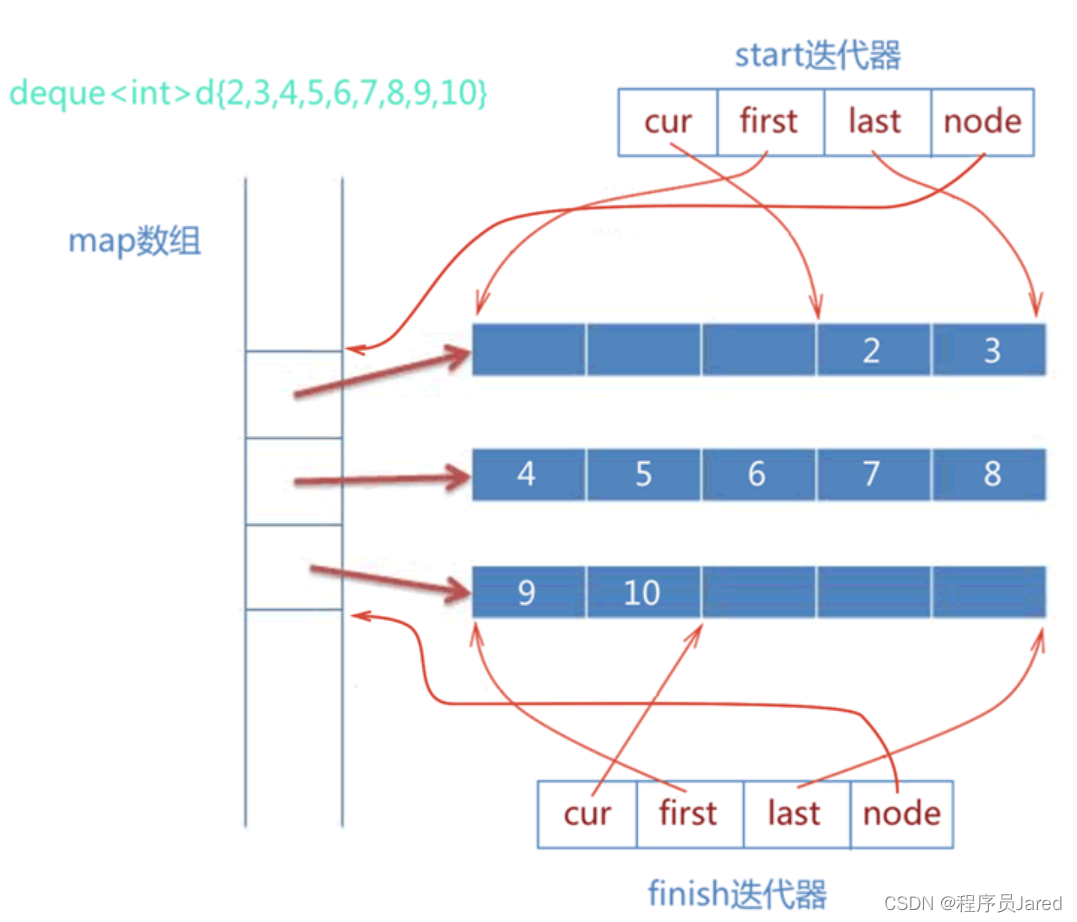
深入浅出C++ ——容器适配器
文章目录一、容器适配器二、deque类简介1. deque的原理2. deque迭代器3. deque的优点和缺陷4. 为什么选择deque作为stack和queue的底层默认容器一、容器适配器 适配器的概念 适配器是STL六大核心组件之一,它是一种设计模式,该种模式是将一个类的接口转换…...
电脑常用知识与工作常用工具
什么是电脑快捷键? 所谓快捷键就是使用键盘上某一个或某几个键的组合完成一条功能命令,从而达到提高操作速度的目的。 键盘布局 主键盘区,数字辅助键盘区、F键功能键盘区、控制键区,对于多功能键盘还增添了快捷键区 一、常用快捷…...
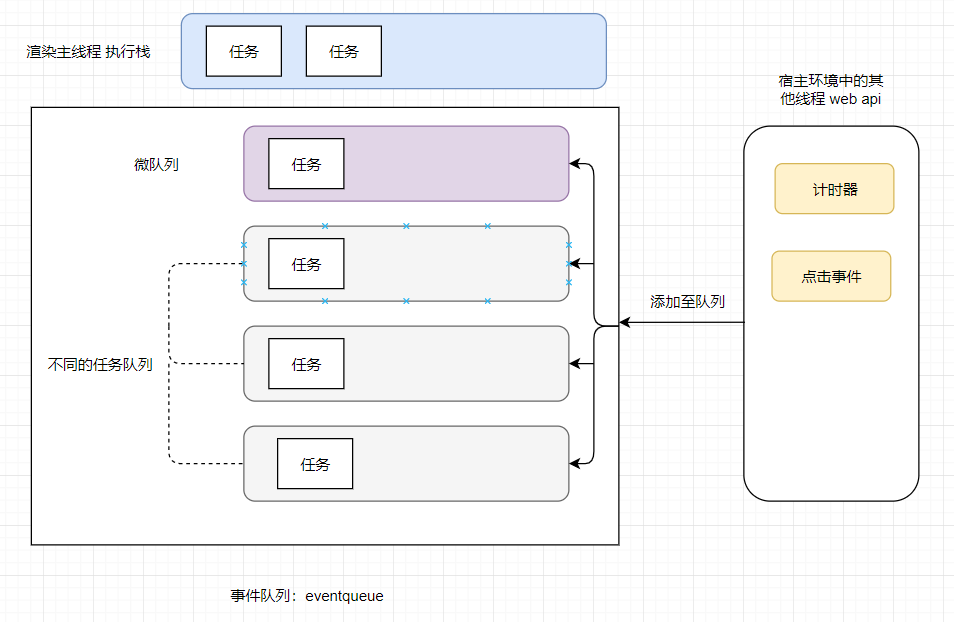
JS的事件循环
文章目录写在前面1.浏览器的进程模型1.1 何为进程1.2 何为线程1.3 浏览器有哪些线程和进程2.渲染主线程是如何工作的任务队列的优先级面试题如何理解JS异步JS中的计时器能做到精确计时吗?为什么?写在前面 此处的文字为自己的理解 1.浏览器的进程模型 1.…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
