LDPC码的编译码原理简述
关于fpga调用ldpc IP
core的相关参数问题可以看我的另一篇文章
LDPC码由Gallager在1962年提出,全称为
Low Density Parity-check Codes 低密度奇偶校验码
它的译码性能可以逼近Shannon信道容量限,广富盛名的Turbo码也被证明是LDPC码的一个特例。并且LDPC码具有在中长码长时超过 Turbo 码的性能,并且具有译码复杂度更低,能够并行译码及译码错误可检测等特点。
LDPC码内容较为复杂,本人由于未学过图论等重要相关知识,难以透彻理解其本质,因此本文主要是介绍以及引用、链接他人的描述。
LDPC编码
ldpc码是一种线性分组码,因此它有生成矩阵和校验矩阵。
我们假设有一个长度为k的信息序列s1∗ks_{1*k}s1∗k,可以通过生成矩阵Gk∗nG_{k*n}Gk∗n得到编码后码长为n的码字
x1∗n=s1∗k⋅Gk∗nx_{1*n} = s_{1*k} · G_{k*n}x1∗n=s1∗k⋅Gk∗n
同时还有一个唯一对应的校验矩阵H(n−k)∗nH_{(n-k)*n}H(n−k)∗n,所有码字满足x1∗n⋅H(n−k)∗nT=01∗(n−k)x_{1*n} · H_{(n-k)*n}^T=0_{1*(n-k)}x1∗n⋅H(n−k)∗nT=01∗(n−k)
和一般的线性分组码不同的是其校验矩阵的稀疏性,即校验矩阵中只有数量很少的元素为“1”大部分都是“0”,这也是它名字“低密度奇偶校验码”的由来。
由于校验矩阵中1很少,所以1的分布就很重要。根据1的分布,LDPC码又可以分为正则LDPC码和非正则LDPC码。
正则LDPC码
Gallager 最早给出了正则 LDPC码的定义,具体来讲正则LDPC码的校验矩阵H满足下面三个条件:
- H的每行有ρ\rhoρ个“1”
- H的每列有λ\lambdaλ个“1”,λ≥3\lambda≥3λ≥3(这样具有较好的汉明距离特性)
- ρ\rhoρ和λ\lambdaλ都远小于H的行数(n-k)和列数(n)
于是校验矩阵可以用(n,λ,ρ)(n,\lambda,\rho)(n,λ,ρ)来表示,下图为一个(20,3,4)的LDPC码校验矩阵
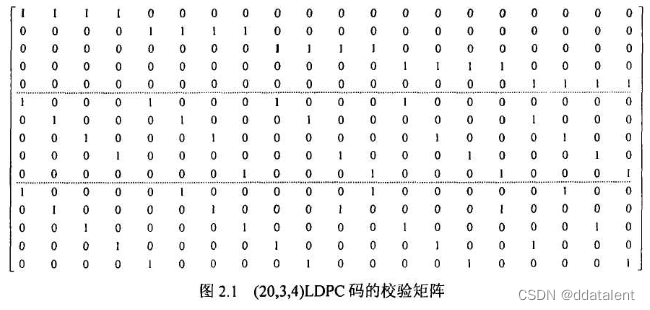
此时我们再回顾表达式x1∗n⋅H(n−k)∗nT=01∗(n−k)x_{1*n} · H_{(n-k)*n}^T=0_{1*(n-k)}x1∗n⋅H(n−k)∗nT=01∗(n−k)
我们可以发现:
矩阵H的每列各自包含λ\lambdaλ个“1”,表示每个码元变量受到相同数目的校验约束;
每行也各自包含ρ\rhoρ个“1”,表示每个校验方程对相同数目的码元变量进行校验约束。
Tanner图结构与非正则LDPC码
思考到这一步,我们可以尝试把校验矩阵换一种方式表达出来。对于上图(20,3,4)的校验矩阵H15∗20H_{15*20}H15∗20来说,15代表15个校验约束,20代表20个码元。
每个校验约束可以约束4个码元,每个码元受到3个校验约束。
我们不妨化画出下图
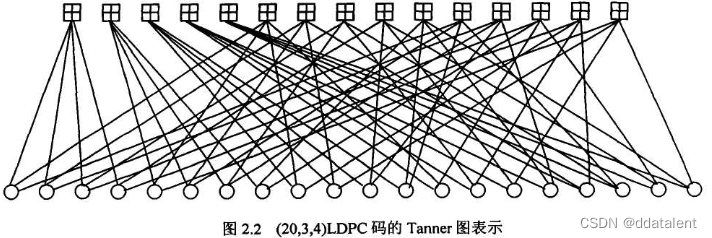
上面一行15个田字表示校验约束,下面一行20个圆形表示码元。
为什么这样表示呢?因为我们发现(n,λ,ρ)(n,\lambda,\rho)(n,λ,ρ)只能用来表示校验矩阵H各列(行)中“1”的个数相同时的矩阵,倘若各列(行)中“1”的个数不相同,就不能如此表示,这就是非正则LDPC码。
Tanner图结构中可以用度分布序列来描述LDPC校验矩阵,本人对此知之甚少,有兴趣的朋友可以学习了解一下。《LDPC码的编译码原理及编码设计》-王鹏-西安电子科技大学
用度分布序列来描述LDPC校验矩阵还有一个好处,因为LDPC码的译码采用的是基于置信传播的软输出 迭代译码算法,在译码过程中,信息的传递是在边上进行的,采用边的分布来描述LDPC码有助于分析其在给定译码算法下的实际性能和理论性能的上下界。
LDPC译码
LDPC码通用的一类译码算法,即所谓的消息传递算法(Message PassingAlgorithms)消息传递算法是一种选代译码算法(Ierative Algorithms ),它的名字来源于其运行机制,在该算法的每一轮选代过程中关于各个节点的置信消息需要在变量节点和校验节点之间传递。
例如由变量节点向校验节点传递的消息是基于变量节点对应的码元变量经过信道后的观察值和由邻接的校验节点在上一次迭代过程中传递过来的消息联合计算的。
由此衍生出的各种译码算法较为复杂,刚刚那篇论文和
这位朋友的博客介绍的比较清楚,推荐大家去学习一下。
引用:
- 王鹏. LDPC码的编译码原理及编码设计[D].西安电子科技大学,2004.
- https://blog.csdn.net/qq_37041791/article/details/119761628
相关文章:

LDPC码的编译码原理简述
关于fpga调用ldpc IP core的相关参数问题可以看我的另一篇文章 LDPC码由Gallager在1962年提出,全称为 Low Density Parity-check Codes 低密度奇偶校验码 它的译码性能可以逼近Shannon信道容量限,广富盛名的Turbo码也被证明是LDPC码的一个特例。并且LDPC…...

网络安全——数链路层据安全协议
作者简介:一名云计算网络运维人员、每天分享网络与运维的技术与干货。 座右铭:低头赶路,敬事如仪 个人主页:网络豆的主页 目录 前言 一.数据链路层安全协议简介 1.数据链路安全性 二.局域网数据链路层协议 1.…...
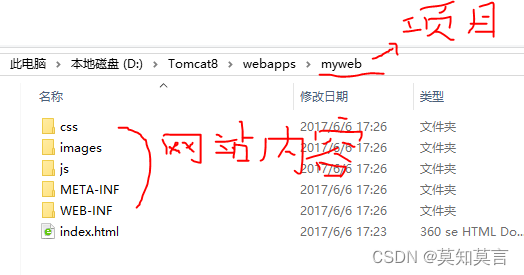
spring的启动过程(一) :IOC容器的启动过程
一、web容器的加载 首先我们要先知道一个web项目的启动过程。 将Web项目部署到Tomcat中的方法之一,是部署没有封装到WAR文件中的Web项目。要使用这一方法部署未打包的webapp目录,只要把我们的项目(编译好的发布项目,非开发项目&am…...
这次,我的CentOS又ping不通www.baidu.com了(gateway配置)
当我们保证了宿主机与虚拟机的ip地址在同一网段,并且我们使用虚拟机ping宿主机,与宿主机ping虚拟机都可以互相ping通的情况下虚拟机却ping不通外网了,由于涉及到了跨越网络访问,所以我们应该把问题聚焦在网关的配置上!…...

启智社区“我为开源狂”第六期活动小白教程之基础活跃榜
一、写在前面 春天来啦~启智社区第六期活动也来啦! 有奖金的哦~~ 基础活跃榜奖金根据用户活跃程度进行100-300元的激励。 挑战升级榜需要用户完成相应任务,达标者可获得300-1000元的激励。 邀请助力榜根据用户邀请情况进行积分累加,按实际达…...

华为OD机试 - 区块链文件转储系统(Python)【2023-Q1 新题】
华为OD机试300题大纲 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 华为OD详细说明:https://dream.blog.csdn.net/article/details/128980730 区块链文件转储系…...

【字节面试】Fail-fast知识点相关知识点
字节面试,问到的一个小知识点,这里做一下总结,其实小编之前有一篇文章,已经对此有过涉及,不过这里知识专项针对于问题,把这个知识点拎出来说一下。 1.问题 什么是Fail-fast机制? Hashmap是否拥…...
git应用笔记(三)
在新增虚拟机linux的基础上,做git的下载与提交 1、初始化自己的用户名和邮箱。 git config --global user.name “输入你的用户名” git config --global user.email “输入你的邮箱” 2、将本地公钥及配置如图1复制粘贴到虚拟机当前用户.ssh\目录下 4929a0205f43…...
有序表的应用:设计一个增、删、查数据的时间复杂度均为O(logN)的结构
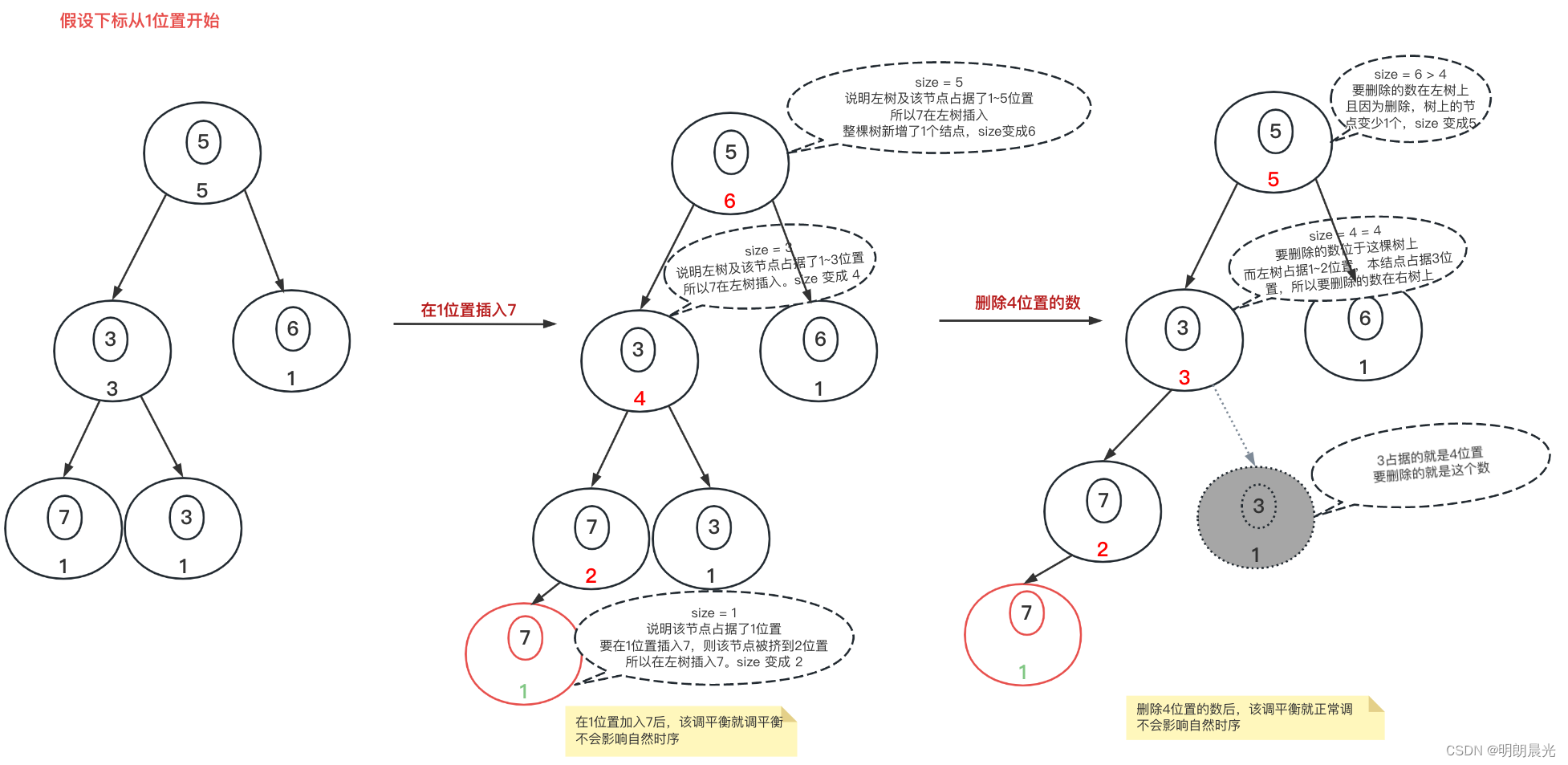
1、题目描述 设计一个结构包含如下三个方法: void add(int index, int num); //把num加入到index位置 int get(int index); //取出index位置的值(是自然序的index位置,非排序后) void remove(int index); //把index位置上的值删…...

离线环境拷贝迁移 conda envs 环境(蛮力方法,3行命令)
前言 最近要使用 GPU 服务器做实验,可惜的是,有网络连接的服务器显卡旧,算力不够;显卡较新的机器没有联网。于是有需求将旧机器上配置好的 conda 环境迁移至新机器。网上给的默认方法生成 yaml 文件迁移等 需要联网,只…...
【数据结构与算法】字符串1:反转字符串I 反转字符串II 反转字符串里的单词 剑指offer(替换空格、左旋转字符串)
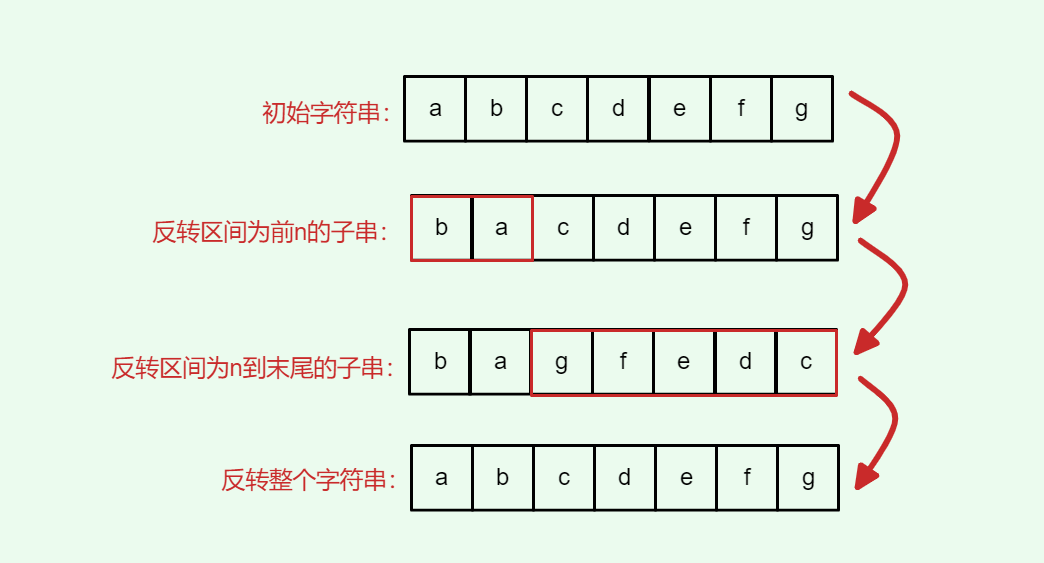
今日任务 344.反转字符串541.反转字符串II剑指Offer 05.替换空格151.反转字符串里的单词剑指Offer58-II.左旋转字符串 1.Leetcode344.反转字符串 来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/reverse-string &#…...
深入浅出C++ ——容器适配器
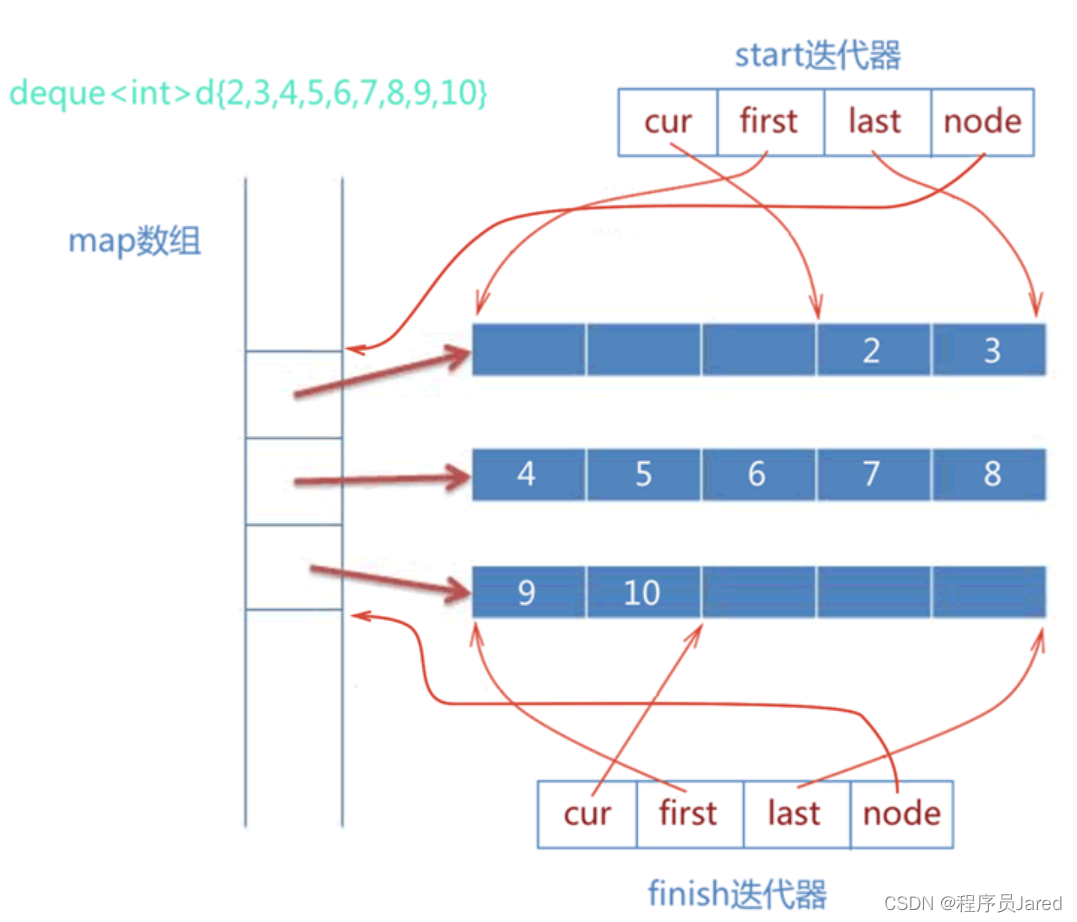
文章目录一、容器适配器二、deque类简介1. deque的原理2. deque迭代器3. deque的优点和缺陷4. 为什么选择deque作为stack和queue的底层默认容器一、容器适配器 适配器的概念 适配器是STL六大核心组件之一,它是一种设计模式,该种模式是将一个类的接口转换…...
电脑常用知识与工作常用工具
什么是电脑快捷键? 所谓快捷键就是使用键盘上某一个或某几个键的组合完成一条功能命令,从而达到提高操作速度的目的。 键盘布局 主键盘区,数字辅助键盘区、F键功能键盘区、控制键区,对于多功能键盘还增添了快捷键区 一、常用快捷…...
JS的事件循环
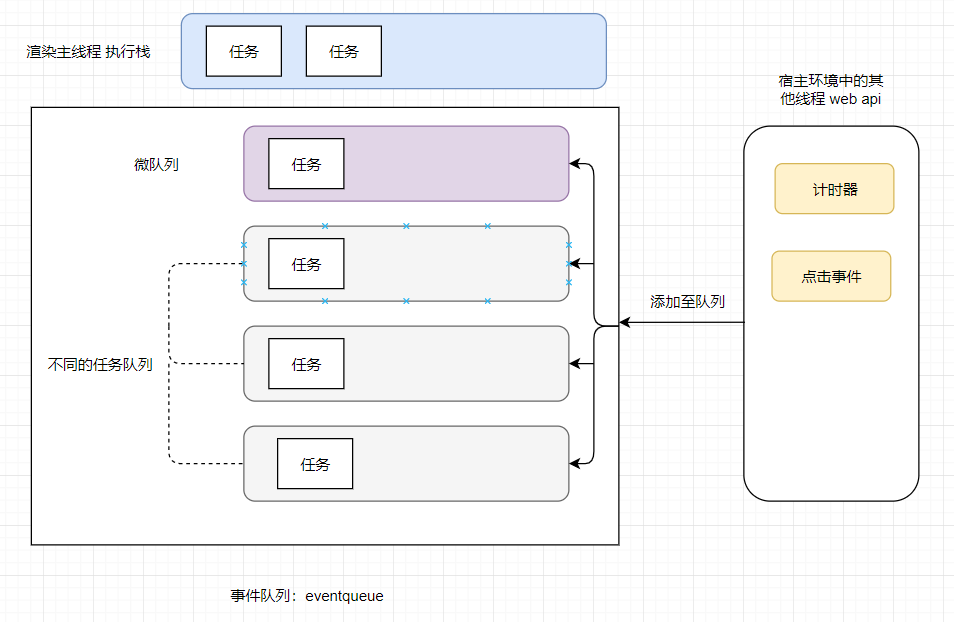
文章目录写在前面1.浏览器的进程模型1.1 何为进程1.2 何为线程1.3 浏览器有哪些线程和进程2.渲染主线程是如何工作的任务队列的优先级面试题如何理解JS异步JS中的计时器能做到精确计时吗?为什么?写在前面 此处的文字为自己的理解 1.浏览器的进程模型 1.…...
【阿旭机器学习实战】【31】股票价格预测案例--线性回归
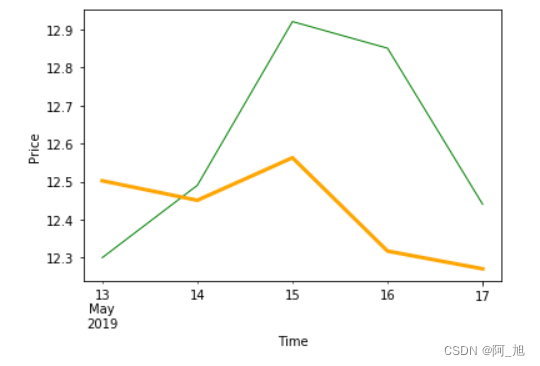
【阿旭机器学习实战】系列文章主要介绍机器学习的各种算法模型及其实战案例,欢迎点赞,关注共同学习交流。 注:本文模型结果不好,仅做学习参考使用,提供思路。了解数据处理思路,训练模型和预测数值的过程。 目录1. 读取数据K线图绘…...

浅谈毫米波技术与应用
浅谈毫米波之技术篇2020年10月GSMA发布的《5G毫米波技术白皮书》预计,在2022年北京冬奥会上,5G毫米波有望大放异彩,为观众、媒体转播者、赛事组织和参与者等提供优质的观赛体验、完备的服务保障,将可提供全景VR、新型信息交互、智…...

给安全平台编写插件模块的思路分享
一、背景 最近在GitHub看到一个新的开源安全工具,可以把工具都集成到一个平台里,觉得挺有意思,但是平台现有的工具不是太全,我想把自己的工具也集成进去,所以研究了一番 蜻蜓安全工作台是一个安全工具集成平台&#x…...

4123版驱动最新支持《霍格沃茨之遗》,英特尔锐炫显卡带你畅游魔法世界
2023年开年最火的3A大作,那一定是近期上架steam平台的《霍格沃茨之遗》,这款游戏在2020年9月份曝光,游戏根据《哈利波特》系列书籍内容改编,作为一款开放式的3A大作,《霍格沃兹之遗》目前在steam上的实时在线人数已经突…...
OSI模型和网络协议简介
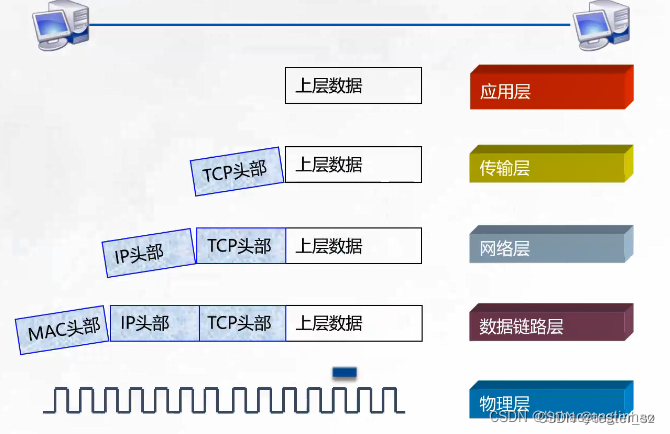
文章目录一、OSI七层模型1.1什么是OSI七层模型?1.2这个网络模型究竟是干什么呢?二、TCP/IP协议三、常见协议四、物联网通信协议以及MQTT4.1 物联网七大通信协议4.2 MQTT特性一、OSI七层模型 1.1什么是OSI七层模型? 我们需要了解互联网的本质…...

传感器原理及应用期末复习汇总(附某高校期末真题试卷)
文章目录一、选择题二、填空题三、简答题四、计算题五、期末真题一、选择题 1.下列哪一项是金属式应变计的主要缺点(A) A、非线性明显 B、灵敏度低 C、准确度低 D、响应时间慢 2.属于传感器动态特性指标的是(D) A、重复性 B、线…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...
