有关时间复杂度和空间复杂度的练习
目录
一、消失的数字
二、轮转数组
三、 单选题
一、消失的数字
数组nums包含从0到n的所有整数,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在 O(n) 时间内完成吗?
注意:本题相对书上原题稍作改动
示例 1:
输入:[3,0,1]
输出:2
示例 2:
输入:[9,6,4,2,3,5,7,0,1]
输出:8
代码实现一(使用异或运算):
int missingNumber(int* nums, int numsSize)
{int ans = 0;for (int i = 0; i <= numsSize; ++i){ans ^= i;}for (int i = 0; i < numsSize; ++i){ans ^= nums[i];}return ans;
}代码实现二(使用等差数列求和公式):
int missingNumber(int* nums, int numsSize)
{int sum = numsSize * (numsSize + 1) / 2;for (int i = 0; i < numsSize; ++i){sum -= nums[i];}return sum;
}以上两种算法的时间复杂度都是 O(n),空间复杂度都是 O(1)。
二、轮转数组
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
提示:
-
1 <= nums.length <= 10^5 -
-2^31 <= nums[i] <= 2^31 - 1 -
0 <= k <= 10^5
进阶:
-
尽可能想出更多的解决方案,至少有 三种 不同的方法可以解决这个问题。
-
你可以使用空间复杂度为
O(1)的 原地 算法解决这个问题吗?
代码实现一:
void rotate(int* nums, int numsSize, int k)
{k %= numsSize;int* tmp = (int*)malloc(sizeof(int) * k);if (NULL == tmp){perror("malloc failed!");return;}// 首先把数组后面的 k 个元素存放到 tmp 指向的临时空间中int j = 0;for (int i = numsSize - k; i < numsSize; ++i){tmp[j++] = nums[i];}// 然后把数组前面的 numsSize - k 个元素按从后往前的顺序依次往后移动 k 个位置for (int i = numsSize - k - 1; i >= 0; --i){nums[i + k] = nums[i];}// 最后再将存放在临时空间中的 k 个元素放回数组中for (int i = 0; i < k; ++i){nums[i] = tmp[i];}free(tmp);tmp = NULL;
}该算法的时间复杂度是 O(n),空间复杂度是 O(k)。
代码实现二:
void reverse(int* nums, int left, int right)
{while (left < right){int tmp = nums[left];nums[left] = nums[right];nums[right] = tmp;++left;--right;}
}
void rotate(int* nums, int numsSize, int k)
{k %= numsSize;reverse(nums, 0, numsSize - k - 1);reverse(nums, numsSize - k, numsSize - 1);reverse(nums, 0, numsSize - 1);
}该算法的时间复杂度是 O(n),空间复杂度是 O(1)。
分析(示例一):
1 2 3 4 | 5 6 7,即根据k将整数数组nums分为左右两个部分。
4 3 2 1 | 7 6 5,它是分别逆序左右两个部分后得到的结果。
5 6 7 | 1 2 3 4,它是整体逆序后得到的结果。在逆序的过程中,越靠后的元素经过逆序后就会越靠前,因此整体逆序后,左右两部分的元素发生了互换,但由于之前已经分别逆序了左右两部分的元素,因此在第 3 步后,两部分的元素的顺序较一开始没有发生改变。
三、 单选题
给定一个整数 sum,从有 n 个有序元素的数组中寻找元素 a, b,使得 a + b 的结果最接近 sum,最快的平均时间复杂度是:
A、O(n)
B、O(nlogn)
C、O(n^2)
D、O(logn)
代码实现(假设数组是按非递减顺序排列):
int* findClosestPair(int* nums, int numsSize, int sum, int* returnSize)
{*returnSize = 2;int* ans = (int*)malloc(sizeof(int) * 2);if (NULL == ans){perror("malloc failed!");return NULL;}int left = 0;int right = numsSize - 1;int dif = INT_MAX;while (left < right){int res = nums[left] + nums[right] - sum;if (abs(res) < dif) // 判断是否更新误差{ans[0] = nums[left];ans[1] = nums[right];dif = abs(res);}if (res < 0) // 此时 nums[left] + nums[x] < res < 0,其中 x < right++left;else if (res > 0) // 此时 nums[right] + nums[x] > res > 0,其中 x > left --right;elsebreak;}return ans;
}该算法的时间复杂度为 O(n),因此正确答案是 A。
相关文章:

有关时间复杂度和空间复杂度的练习
目录 一、消失的数字 二、轮转数组 三、 单选题 一、消失的数字 数组nums包含从0到n的所有整数,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在 O(n) 时间内完成吗? 注意:本题相对书上原题稍作改动 示例 1: 输入…...

linux服务器nfs数据挂载
参考:https://blog.csdn.net/qq_43721935/article/details/119889841?from_wecom1 1、NFS 介绍 NFS 即网络文件系统(Network File-System),可以通过网络让不同机器、不同系统之间可以实现文件共享。通过 NFS,可以访问…...

Python 自动化测试必会技能板块—unittest框架
说到 Python 的单元测试框架,想必接触过 Python 的朋友脑袋里第一个想到的就是 unittest。的确,作为 Python 的标准库,它很优秀,并被广泛应用于各个项目。但其实在 Python 众多项目中,主流的单元测试框架远不止这一个。…...

mysql存储引擎、事务、索引
目录MySQL进阶存储引擎什么是存储引擎常用存储引擎事务什么是事务怎么理解提交事务 和回滚事务事务特性事务的隔离级别索引什么是索引索引的实现原理什么条件下,我们会考虑给字段添加索引呢?什么条件下,索引会失效?索引分类MySQL进阶 存储引…...
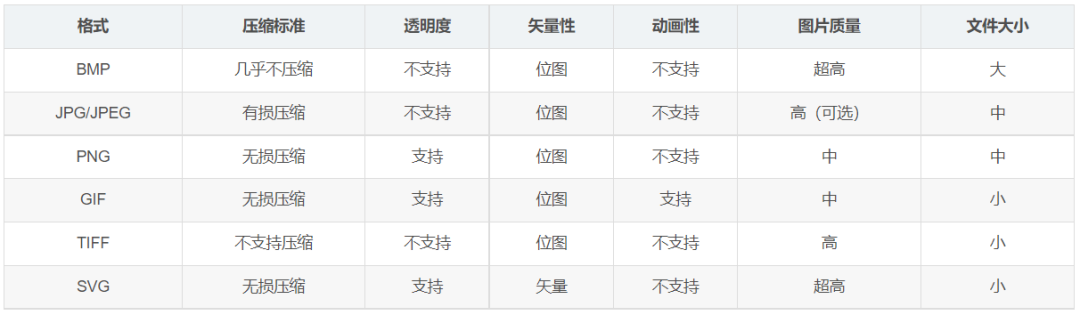
毕业论文图片格式、分辨率选择及高质量Word转PDF方法
已知1:毕业论文盲评通常需要提交PDF文件。 已知2:PDF文件太大可能会导致翻页卡顿以及上传盲评网站失败。 已知3:Word转PDF方法不当可能会导致图像模糊。 已知4:打印机分辨率通常为300dpi。 问题1:论文插图分辨率设置…...
华为外包测试2年,不甘被替换,168天的学习转岗成正式员工
我25岁的时候,华为外包测试,薪资13.5k,人在深圳。 内卷什么的就不说了,而且人在外包那些高级精英年薪大几十的咱也接触不到,就说说外包吧。假设以我为界限,25岁一线城市13.5k,那22-24大部分情况…...
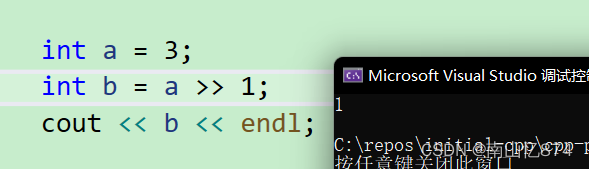
简单的C++:【运算符重载】新手易学
学过C语言的同志们应该都知道位运算符>> 和 << (右移左移),但是这两个运算符在C中还是我们的输入和输出流操作符,那么这是为什么呢?,了解完本篇文章之后,我们再来回答这个问题。 C为…...
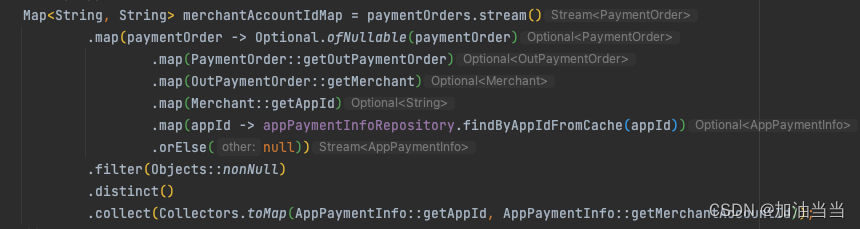
NPE:记一次脑残NPE的排查过程
目录 碎碎念: 如下这行报NPE: 排查过程: 解解方案: 小结: 空指针出现的几种情况: 如何从根源避免空指针: 赋值时自动拆箱出现空指针: 1、变量赋值自动拆箱出现的空指针 2、…...
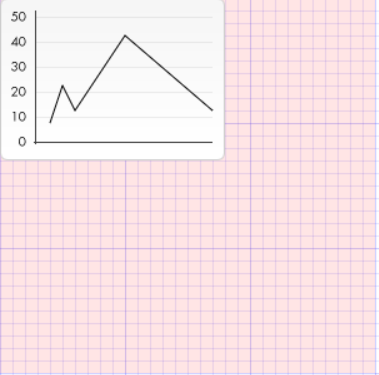
canvas样式与颜色,字体,图片,状态,形变
色彩 fillStyle color 设置图形的填充颜色。 strokeStyle color 设置图形轮廓的颜色。 备注: 一旦您设置了 strokeStyle 或者 fillStyle 的值,那么这个新值就会成为新绘制的图形的默认值。如果你要给每个图形上不同的颜色,你需要重新设置…...
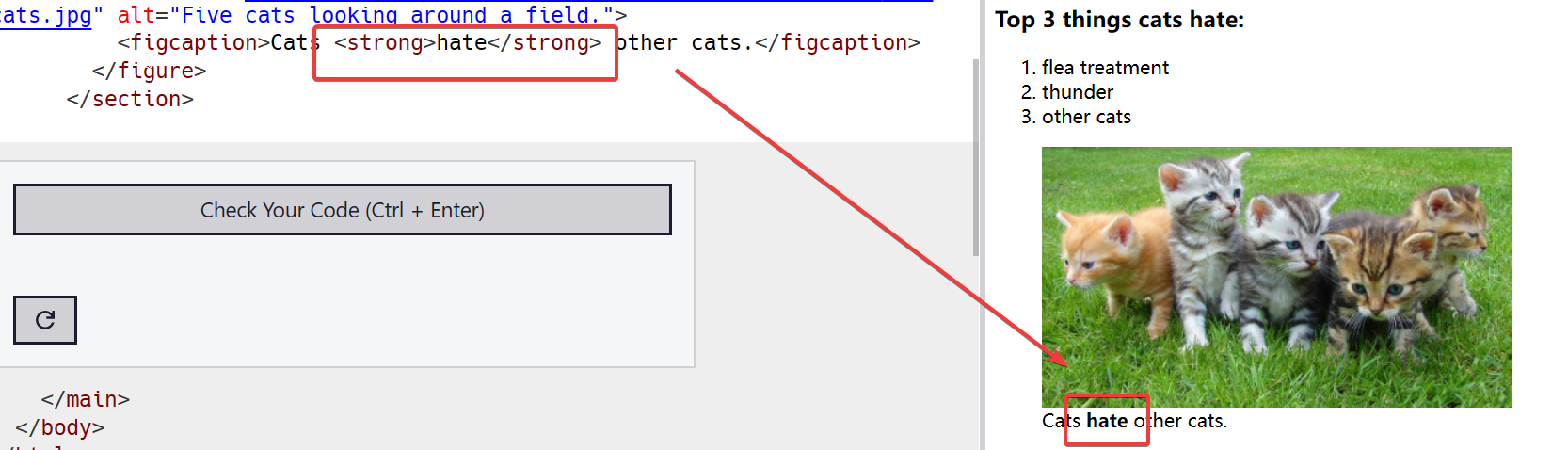
重识html
html 重识html 万维网用url统一资源定位符标识分布因特网上的各种文档 各种概念 URL: 统一资源定位器 它是WWW的统一资源定位标志,就是指网络地址 在WWW上,每一信息资源都有统一的且在网上唯一的地址 网页: 由文字 图片 视频 音乐各种元素排列组…...
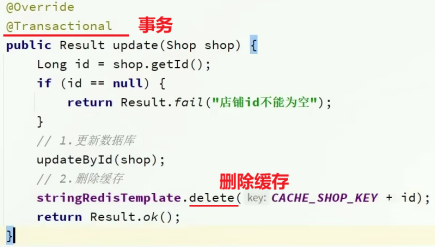
Redis:缓存一致性问题(缓存更新策略)
Redis缓存的一致性1. 缓存1.1 缓存的作用:1.2 缓存的成本:2. 缓存模型3. 缓存一致性问题3.1 引入3.2 解决(1) 先更新数据库,再手动删除缓存(2) 使用事务保证原子性(3) 以Redis中的TTL为兜底3.3 案例:商铺信息查询和更新(1) 查询商…...

spring之声明式事务开发
文章目录一、声明式事务之全注解式开发1、新建springConfig类2、测试程序3、测试结果二、声明式事务之XML实现方式1、配置步骤2、测试程序3、运行结果附一、声明式事务之全注解式开发 基于之前的银行转账系统,将spring.xml配置文件嘎掉,变成全注解式开发…...
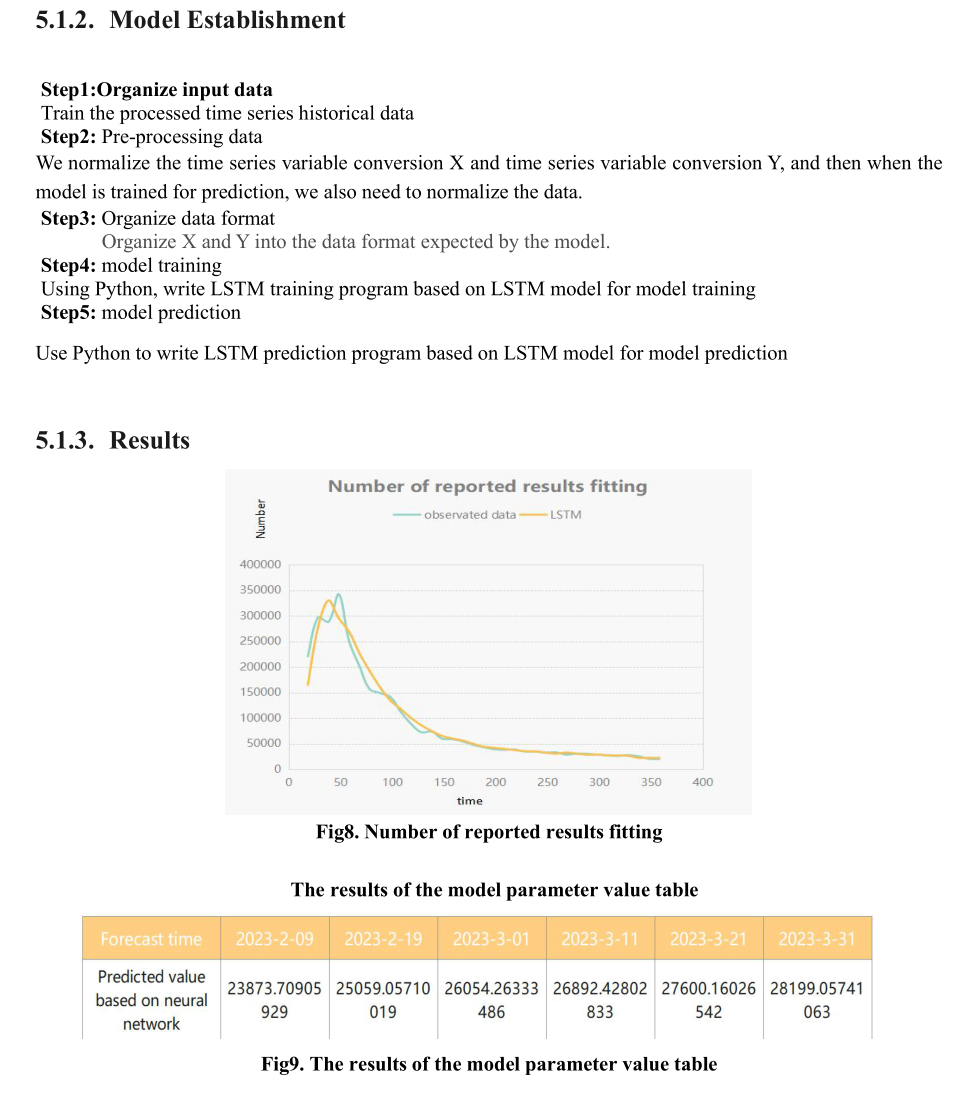
2023美赛参赛经历分享
今天早上登录MCM: The Mathematical Contest in Modeling (comap.com)发现论文提交已经显示Received。虽然这几天连连有开学恶补的期末考试,但还是忙里偷闲趁着新鲜写一篇关于美赛的参赛个人感受。跟我一起打这次美赛的都是软件等专业的hxd,他们之前没有…...

Elasticsearch在Linux中的单节点部署和集群部署
目录一、Elasticsearch简介二、Linux单节点部署1、软件下载解压2、创建用户3、修改配置文件4、切换到刚刚创建的用户启动软件5、测试三、Linux集群配置1、拷贝文件2、修改配置文件3、分别修改文件所有者4、启动三个软件5、测试四、问题总结1、在elasticsearch启动时如果报错内存…...

Scala的变量声明
文章目录变量声明(一)简单说明(二)利用val声明变量1,声明方式2,案例演示(三)利用var声明变量1,声明方式2,案例演示(四)换行输入语句&a…...

面试了字节、美团、腾讯等30几家公司后,才知道软件测试面试全是这个套路......
一、Linux系统应用和环境配置: 1、Linux系统的操作命令给我说10个,一般用什么工具远程连接Linux服务器? 2、Linux中的日志存储在哪里?怎么查看日志内容? 3、Linux中top和ps命令的区别? 4、Linux命令运行…...
Anaconda环境配置
1.进入清华大学镜像网站Index of /anaconda/archive/ | 清华大学开源软件镜像站 | Tsinghua Open Source Mirror,下载稳定版Anaconda3-5.2.0,如下图。2.放到整理好的文件夹中,双击安装包进行安装。3.安装过程中需要改变的默认值如下ÿ…...
Markdown编辑器使用方法
这里写自定义目录标题欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题,有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants创建一个自定义列表如何创建一个注…...
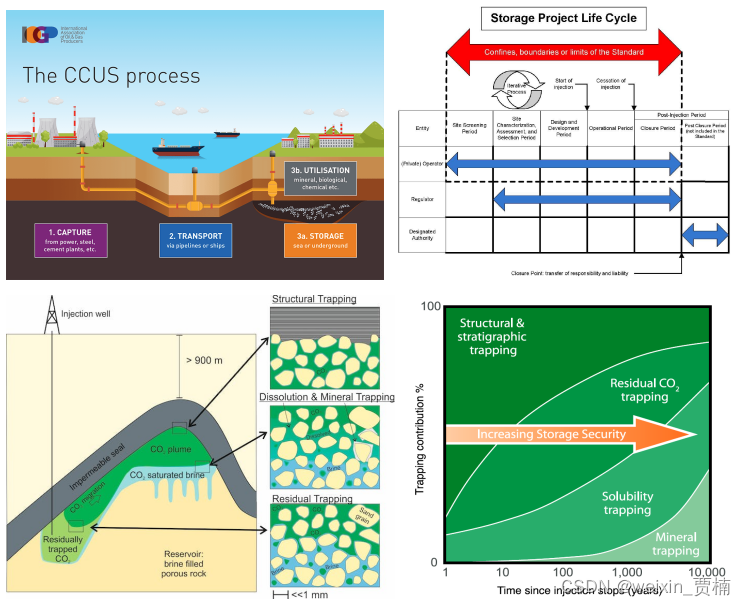
“双碳”目标下二氧化碳地质封存技术应用前景及模型构建实践方法与讨论
我国二氧化碳地质封存技术起步较晚,目前仍没有一套相对完整的行业规范;且就该技术而言,涉及环节众多,理论相对复杂,对于行业的新入局者不太友好。因此,结合时代背景,我们首次尝试对二氧化碳地质…...

算法笔记(十二)—— Manacher算法(回文子串)
计算字符串内的最大回文子串,常用的暴力扩散在应对长度为偶数的回文时会遇到一些问题。 Manacher基础:对字符串进行填充,在字符串开头结尾以及字符间填充‘#’,以来应对偶数回文时的问题。(这是采用暴力扩再除2&#x…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
