【数据结构】栈、队列和数组
栈、队列和数组
- 栈
- 队列
- 数组
- 数组的顺序表示和实现
- 顺序表中查找和修改数组元素
- 矩阵的压缩存储
- 特殊矩阵
- 稀疏矩阵
栈

初始化
#define MaxSize 50//栈中元素的最大个数
typedef char ElemType;//数据结构
typedef struct{int top;//栈顶指针ElemType data[MaxSize];//存放栈中的元素
}SqStack;//初始化栈,给top赋值为-1
void InitStack(SqStack *stack){stack->top = -1;
}
判断是否为空
//判断栈是否为空,空返回true,反之即返回false
bool StackEmpty(SqStack stack){if(stack.top==-1) return true;return false;
}
进栈
//进栈
bool Push(SqStack *stack,ElemType e){//判断是否满栈if(stack->top==MaxSize-1) return false;//指针先加1,再入栈stack->data[++stack->top]=e;return true;
}
出栈
//出栈
ElemType Pop(SqStack *stack){//判断是否为空栈if(stack->top==-1) return false;//先取值,再自减return stack->data[stack->top--];
}
读取栈顶元素
//读取栈顶元素
ElemType GetTop(SqStack stack){//判断是否为空栈if(stack.top==-1) return false;return stack.data[stack.top];
}
队列

初始化
#define MaxSize 5
typedef char ElemType;typedef struct
{ElemType data[MaxSize];int rear,front;
}SqQueue;//初始化
void InitQueue(SqQueue *queue){queue->front = queue->rear=0;
}
判断空
//判断是否为空,即判断首尾指针是否相等
bool QueueEmpty(SqQueue queue){if(queue.front==queue.rear) return true;return false;
}
入队
//入队
bool EnQueue(SqQueue *queue,ElemType e){//判断是否是满队,即尾指针的下一个指向首指针if((queue->rear+1)%MaxSize==queue->front) return false;queue->data[queue->rear]=e;//赋值//尾指针+1取模queue->rear = (queue->rear+1)%MaxSize;return true;
}
出队
//出队
ElemType DeQueue(SqQueue *queue){//判断是否为空if(queue->front==queue->rear) return false;//先取值,首指针再+1取模ElemType e = queue->data[queue->front];queue->front++;return e;
}
数组
提到数组,大家首先会想到的是:很多编程语言中都提供有数组这种数据类型,比如 C/C++、Java、Go、C# 等。但本节我要讲解的不是作为数据类型的数组,而是数据结构中提供的一种叫数组的存储结构。
和线性存储结构相比,数组最大的不同是:它存储的数据可以包含多种“一对一”的逻辑关系。举个简单的例子:

上图中,{a1, a2, a3, a4}、{b1, b2, b3, b4}、{c1, c2, c3, c4}、{d1, d2, d3, d4} 中各自包含的元素具有“一对一”的逻辑关系,同时 a、b、c、d 这 4 个序列也具有“一对一”的逻辑关系。
这样存储不止一种“一对一”逻辑关系的数据,数据结构就推荐使用数组存储结构。
对于数组存储结构,我们可以这样理解它:数组是对线性表的扩展,是一种“特殊”的线性存储结构,用来存储具有多种“一对一”逻辑关系的数据。
实际场景中,存储具有 N 种“一对一”逻辑关系的数据,通常会建立 N 维数组:
- 一维数组和其它线性存储结构很类似,用来存储只有一种“一对一”逻辑关系的数据:

- 二维数组用来存储包含两种“一对一”逻辑关系的数据。二维数组可以看作是存储一维数组的一维数组

- n 维数组用来存储包含 n 种“一对一”逻辑关系的数据,可以看作是存储 n-1 维数组的一维数组;
数组存储结构还具有一些其它的特性,包括:
- 无论数组的维度是多少,数组中的数据类型都必须一致;
- 数组一旦建立,它的维度将不再改变;
- 数组存储结构不会对内部的元素做插入和删除操作,常见的操作有 4 种,分别是初始化数组、销毁数组、取数组中的元素和修改数组中的元素。
数组的顺序表示和实现
数组可以是多维的,而顺序表只能是一维的线性空间。要想将 N 维的数组存储到顺序表中,可以采用以下两种方案:
- 以列序为主(先列后行):按照行号从小到大的顺序,依次存储每一列的元素;
- 以行序为主(先行后序):按照列号从小到大的顺序,依次存储每一行的元素。
多维数组中,最常用的是二维数组,接下里就以二维数组为例,讲解数组的顺序存储结构。

所示的二维数组按照“列序为主”的方案存储时,数组中的元素在顺序表中的存储状态如下图所示:

同样的道理,按照“行序为主”的方案存储数组时,各个元素在顺序表中的存储状态如图

顺序表中查找和修改数组元素
注意,只有在顺序表内查找到数组中的目标元素之后,才能对该元素执行读取和修改操作。
在 N 维数组中查找目标元素,需知道以下信息:
- 数组的存储方式;
- 数组在内存中存放的起始地址;
- 目标元素在数组中的坐标。比如说,二维数组中是通过行标和列标来确定元素位置的;
- 数组中元素的类型,即数组中单个数据元素所占内存的大小,通常用字母 L 表示;
根据存储方式的不同,查找目标元素的方式也不同。仍以二维数组为例,如果数组采用“行序为主”的存储方式,则在二维数组 anm 中查找 aij 位置的公式为:
LOC(i, j) = LOC(0, 0) + (i * m + j) * L;
其中,LOC(i, j) 为 aij 在内存中的地址,LOC(0, 0) 为二维数组在内存中存放的起始位置(也就是 a00 的位置)。
而如果采用以列存储的方式,在 anm 中查找 aij 的方式为:
LOC(i, j) = LOC(0, 0) + (j * n + i) * L;
根据以上两个公式,就可以在顺序表中找到目标元素,自然也就可以进行读取和修改操作了。
代码实现
#include<stdarg.h>
#include<malloc.h>
#include<stdio.h>
#include<stdlib.h> // atoi()
#include<io.h> // eof()
#include<math.h>#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW 3
#define UNDERFLOW 4
typedef int Status; //Status是函数的类型,其值是函数结果状态代码,如OK等
typedef int Boolean; //Boolean是布尔类型,其值是TRUE或FALSE
typedef int ElemType;#define MAX_ARRAY_DIM 8 //假设数组维数的最大值为8
typedef struct
{ElemType* base; //数组元素基址,由InitArray分配int dim; //数组维数int* bounds; //数组维界基址,由InitArray分配int* constants; // 数组映象函数常量基址,由InitArray分配
} Array;Status InitArray(Array* A, int dim, ...)
{//若维数dim和各维长度合法,则构造相应的数组A,并返回OKint elemtotal = 1, i; // elemtotal是元素总值va_list ap;if (dim<1 || dim>MAX_ARRAY_DIM)return ERROR;(*A).dim = dim;(*A).bounds = (int*)malloc(dim * sizeof(int));if (!(*A).bounds)exit(OVERFLOW);va_start(ap, dim);for (i = 0; i < dim; ++i){(*A).bounds[i] = va_arg(ap, int);if ((*A).bounds[i] < 0)return UNDERFLOW;elemtotal *= (*A).bounds[i];}va_end(ap);(*A).base = (ElemType*)malloc(elemtotal * sizeof(ElemType));if (!(*A).base)exit(OVERFLOW);(*A).constants = (int*)malloc(dim * sizeof(int));if (!(*A).constants)exit(OVERFLOW);(*A).constants[dim - 1] = 1;for (i = dim - 2; i >= 0; --i)(*A).constants[i] = (*A).bounds[i + 1] * (*A).constants[i + 1];return OK;
}Status DestroyArray(Array* A)
{//销毁数组Aif ((*A).base){free((*A).base);(*A).base = NULL;}elsereturn ERROR;if ((*A).bounds){free((*A).bounds);(*A).bounds = NULL;}elsereturn ERROR;if ((*A).constants){free((*A).constants);(*A).constants = NULL;}elsereturn ERROR;return OK;
}Status Locate(Array A, va_list ap, int* off) // Value()、Assign()调用此函数 */
{//若ap指示的各下标值合法,则求出该元素在A中的相对地址offint i, ind;*off = 0;for (i = 0; i < A.dim; i++){ind = va_arg(ap, int);if (ind < 0 || ind >= A.bounds[i])return OVERFLOW;*off += A.constants[i] * ind;}return OK;
}Status Value(ElemType* e, Array A, ...) //在VC++中,...之前的形参不能是引用类型
{//依次为各维的下标值,若各下标合法,则e被赋值为A的相应的元素值va_list ap;Status result;int off;va_start(ap, A);if ((result = Locate(A, ap, &off)) == OVERFLOW) //调用Locate()return result;*e = *(A.base + off);return OK;
}Status Assign(Array* A, ElemType e, ...)
{//依次为各维的下标值,若各下标合法,则将e的值赋给A的指定的元素va_list ap;Status result;int off;va_start(ap, e);if ((result = Locate(*A, ap, &off)) == OVERFLOW) //调用Locate()return result;*((*A).base + off) = e;return OK;
}int main()
{Array A;int i, j, k, * p, dim = 3, bound1 = 3, bound2 = 4, bound3 = 2; //a[3][4][2]数组ElemType e, * p1;InitArray(&A, dim, bound1, bound2, bound3); //构造3*4*2的3维数组Ap = A.bounds;printf("A.bounds=");for (i = 0; i < dim; i++) //顺序输出A.boundsprintf("%d ", *(p + i));p = A.constants;printf("\nA.constants=");for (i = 0; i < dim; i++) //顺序输出A.constantsprintf("%d ", *(p + i));printf("\n%d页%d行%d列矩阵元素如下:\n", bound1, bound2, bound3);for (i = 0; i < bound1; i++){for (j = 0; j < bound2; j++){for (k = 0; k < bound3; k++){Assign(&A, i * 100 + j * 10 + k, i, j, k); // 将i*100+j*10+k赋值给A[i][j][k]Value(&e, A, i, j, k); //将A[i][j][k]的值赋给eprintf("A[%d][%d][%d]=%2d ", i, j, k, e); //输出A[i][j][k]}printf("\n");}printf("\n");}p1 = A.base;printf("A.base=\n");for (i = 0; i < bound1 * bound2 * bound3; i++) //顺序输出A.base{printf("%4d", *(p1 + i));if (i % (bound2 * bound3) == bound2 * bound3 - 1)printf("\n");}DestroyArray(&A);return 0;
}
矩阵的压缩存储
特殊矩阵
这里所说的特殊矩阵,主要分为以下两类:
- 含有大量相同数据元素的矩阵,比如对称矩阵;
- 含有大量 0 元素的矩阵,比如稀疏矩阵、上(下)三角矩阵;
针对以上两类矩阵,数据结构的压缩存储思想是:矩阵中的相同数据元素(包括元素 0)只存储一个

数据元素沿主对角线对应相等,这类矩阵称为对称矩阵,矩阵中有两条对角线,对角线称为主对角线,另一条从左下角到右上角的对角线为副对角线。对称矩阵指的是各数据元素沿主对角线对称的矩阵。
对称矩阵的实现过程是,若存储下三角中的元素,只需将各元素所在的行标 i 和列标 j 代入下面的公式:

存储上三角的元素要将各元素的行标 i 和列标 j 代入另一个公式:

最终求得的 k 值即为该元素存储到数组中的位置(矩阵中元素的行标和列标都从 1 开始)。
例如,在数组 skr[6] 中存储图 1 中的对称矩阵,则矩阵的压缩存储状态如图所示(存储上三角和下三角的结果相同):

注意,以上两个公式既是用来存储矩阵中元素的,也用来从数组中提取矩阵相应位置的元素。例如,如果想从图中的数组提取矩阵中位于 (3,1) 处的元素,由于该元素位于下三角,需用下三角公式获取元素在数组中的位置,即:

稀疏矩阵

如果矩阵中分布有大量的元素 0,即非 0 元素非常少,这类矩阵称为稀疏矩阵。
压缩存储稀疏矩阵的方法是:只存储矩阵中的非 0 元素,与前面的存储方法不同,稀疏矩阵非 0 元素的存储需同时存储该元素所在矩阵中的行标和列标。
例如,存储上图中的稀疏矩阵,需存储以下信息:
- (1,1,1):数据元素为 1,在矩阵中的位置为 (1,1);
- (3,3,1):数据元素为 3,在矩阵中的位置为 (3,1);
- (5,2,3):数据元素为 5,在矩阵中的位置为 (2,3);
- 除此之外,还要存储矩阵的行数 3 和列数 3;

**若对其进行压缩存储,矩阵中各非 0 元素的存储状态如图 **

三元组的结构体
//三元组结构体
typedef struct {int i,j;//行标i,列标jint data;//元素值
}triple;
由于稀疏矩阵中非 0 元素有多个,因此需要建立 triple 数组存储各个元素的三元组。除此之外,考虑到还要存储矩阵的总行数和总列数,因此可以采用以下结构表示整个稀疏矩阵:
#define number 20
//矩阵的结构表示
typedef struct {triple data[number];//存储该矩阵中所有非0元素的三元组int mu, nu, tu;//mu和nu分别记录矩阵的行数和列数,tu记录矩阵中所有的非0元素的个数
}TSMatrix;
#include<stdio.h>
#define NUM 3
//存储三元组的结构体
typedef struct {int i, j;int data;
}triple;
//存储稀疏矩阵的结构体
typedef struct {triple data[NUM];int mu, nu, tu;
}TSMatrix;
//输出存储的稀疏矩阵
void display(TSMatrix M);
int main() {TSMatrix M;M.mu = 3;M.nu = 3;M.tu = 3;M.data[0].i = 1;M.data[0].j = 1;M.data[0].data = 1;M.data[1].i = 2;M.data[1].j = 3;M.data[1].data = 5;M.data[2].i = 3;M.data[2].j = 1;M.data[2].data = 3;display(M);return 0;
}
void display(TSMatrix M) {int i, j, k;for (i = 1; i <= M.mu; i++) {for (j = 1; j <= M.nu; j++) {int value = 0;for (k = 0; k < M.tu; k++) {if (i == M.data[k].i && j == M.data[k].j) {printf("%d ", M.data[k].data);value = 1;break;}}if (value == 0)printf("0 ");}printf("\n");}
}
相关文章:

【数据结构】栈、队列和数组
栈、队列和数组 栈队列数组数组的顺序表示和实现顺序表中查找和修改数组元素 矩阵的压缩存储特殊矩阵稀疏矩阵 栈 初始化 #define MaxSize 50//栈中元素的最大个数 typedef char ElemType;//数据结构 typedef struct{int top;//栈顶指针ElemType data[MaxSize];//存放栈中的元…...

python算法调用方案
1、python算法部署方案 (1)独立部署 算法端和应用端各自独立部署。 使用WSGI(flask)web应用A包装算法,并发布该应用A。 应用端B 通过httpclient调用算法应用A中的api接口。 (2)统一部署 算法…...

《微服务架构设计模式》第二章
文章目录 微服务架构是什么软件架构是什么软件架构的定义软件架构的41视图模型为什么架构如此重要 什么是架构风格分层式架构风格六边形架构风格微服务架构风格什么是服务什么是松耦合共享类库的角色 为应用程序定义微服务架构识别操作系统根据业务能力进行拆分业务能力定义了一…...
taro vue3 ts nut-ui 项目
# 使用 npm 安装 CLI $ npm install -g tarojs/cli 查看 Taro 全部版本信息 可以使用 npm info 查看 Taro 版本信息,在这里你可以看到当前最新版本 npm info tarojs/cli 项目初始化 使用命令创建模板项目: taro init 项目名 taro init myApp …...
【群答疑】jmeter关联获取上一个请求返回的字符串,分割后保存到数组,把数组元素依次作为下一个请求的入参...
一个非常不错的问题,来检验下自己jmeter基本功 可能有同学没看懂题,这里再解释一下,上面问题需求是:jmeter关联获取上一个请求返回的字符串,分割后保存到数组,把数组元素依次作为下一个请求的入参 建议先自…...
)
Shell 函数详解(函数定义、函数调用)
Shell 函数的本质是一段可以重复使用的脚本代码,这段代码被提前编写好了,放在了指定的位置,使用时直接调取即可。 Shell 中的函数和C、Java、Python、C# 等其它编程语言中的函数类似,只是在语法细节有所差别。 Shell 函数定义的语…...

git-命令行显示当前目录分支
1. 打开家目录.bashrc隐藏文件,找到如下内容 forlinxubuntu:~$ vi ~/.bashrcif [ "$color_prompt" yes ]; thenPS1${debian_chroot:($debian_chroot)}\[\033[01;32m\]\u\h\[\033[00m\]:\[\033[01;34m\]\w\[\033[00m\]\$ elsePS1${debian_chroot:($debi…...

pgsql 报错 later table “drop column” is not supported now
报错 使用pgsql执行下面的SQL报错 alter table test_user drop clolumn name;报错信息: later table “drop column” is not supported now。 报错原因 hologres pgsql的数据库: 删除列目前还是灰度测试阶段,需要在sql前加上set hg_ex…...

如何制定私域流量布局计划?
01 确定目标用户群体 首先,明确目标用户是私域流量布局的基础。可以通过市场调研、用户画像和数据分析等方式,了解目标用户的年龄、性别、兴趣爱好等特征,为后续精准营销奠定基础。 02 选择合适的私域流量渠道 根据目标用户群体的特点&…...
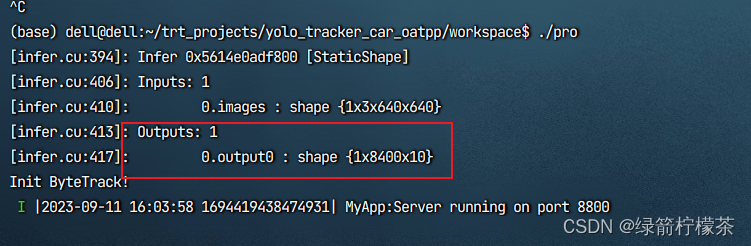
yolov8 模型部署--TensorRT部署-c++服务化部署
写目录 yolov8 模型部署--TensorRT部署1、模型导出为onnx格式2、模型onnx格式转engine 部署 yolov8 模型部署–TensorRT部署 1、模型导出为onnx格式 如果要用TensorRT部署YOLOv8,需要先使用下面的命令将模型导出为onnx格式: yolo export modelyolov8n.p…...
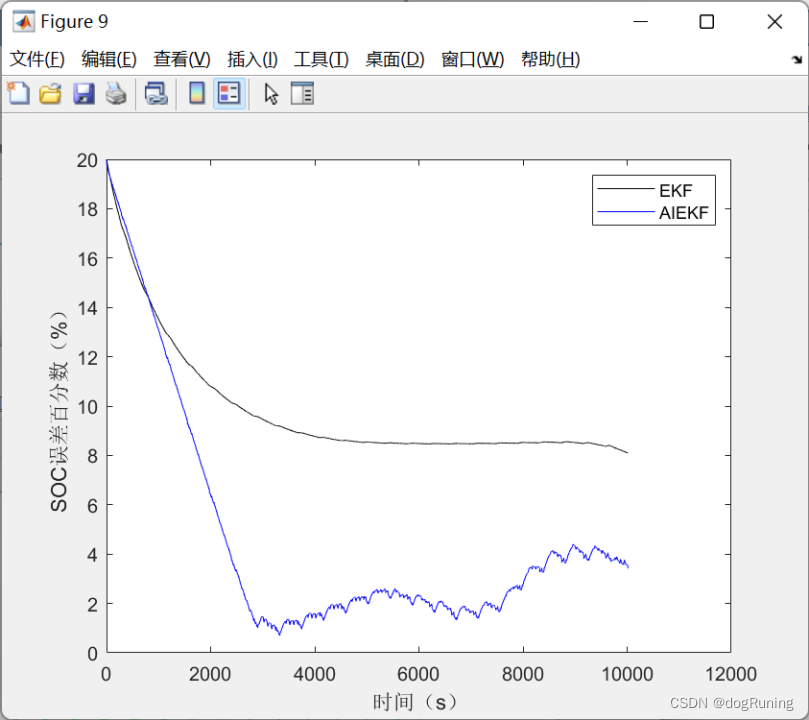
自适应迭代扩展卡尔曼滤波算法AIEKF估计SOC VS 扩展卡尔曼估计SOC
自适应迭代扩展卡尔曼滤波算法(AIEK) 自适应迭代扩展卡尔曼滤波算法(AIEK)是一种滤波算法,其目的是通过迭代过程来逐渐适应不同的状态和环境,从而优化滤波效果。 该算法的基本思路是在每一步迭代过程中&a…...

2023-亲测有效-git clone失败怎么办?用代理?加git?
git 克隆不下来,超时 用以下格式: git clone https://ghproxy.com/https://github.com/Tencent/ncnn.git 你的网站前面加上 https://ghproxy.com/ 刷的一下就下完了!!...

An Empirical Study of GPT-3 for Few-Shot Knowledge-Based VQA
本文是LLM系列文章,针对《An Empirical Study of GPT-3 for Few-Shot Knowledge-Based VQA》的翻译。 GPT-3对基于小样本知识的VQA的实证研究 摘要引言相关工作方法OK-VQA上的实验VQAv2上的实验结论 摘要 基于知识的视觉问答(VQA)涉及回答需…...
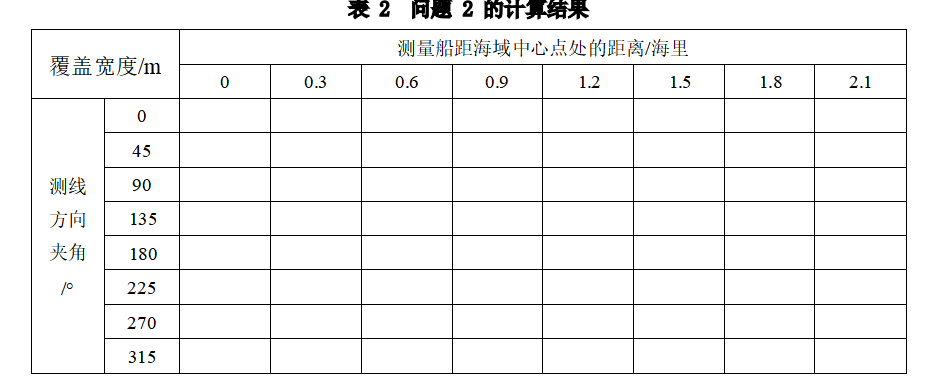
2023高教社杯数学建模B题思路分析 - 多波束测线问题
# 1 赛题 B 题 多波束测线问题 单波束测深是利用声波在水中的传播特性来测量水体深度的技术。声波在均匀介质中作匀 速直线传播, 在不同界面上产生反射, 利用这一原理,从测量船换能器垂直向海底发射声波信 号,并记录从声波发射到…...

02-docker network
Docker网络 Docker网络是什么 Docker 网络是 Docker 容器之间进行通信和连接的网络环境。在 Docker 中,每个容器都有自己的网络命名空间,这意味着每个容器都有自己的网络接口、IP 地址和网络配置 Docker网络启动后,会在宿主机中建立一个名…...

栈和队列经典笔试题
文章目录 栈和队列的回顾💻栈🩳队列👟 栈和队列经典笔试题🔋有效的括号🎸用队列实现栈 🕯用栈实现队列🔭设计循环队列🧼 安静的夜晚 你在想谁吗 栈和队列的回顾💻 栈&am…...

No5.9:多边形内角和公式
#!/usr/bin/python # -*- coding: UTF-8 -*-#指定了编码,中文就能正常展示 # codingutf-8def calc_degree(n):#n代表边形的总数degree (n - 2) * 180#多边形内角和公式return degreeprint(calc_degree(3))#三角形的内角和 print(calc_degree(4))#四边形的内角和【小…...
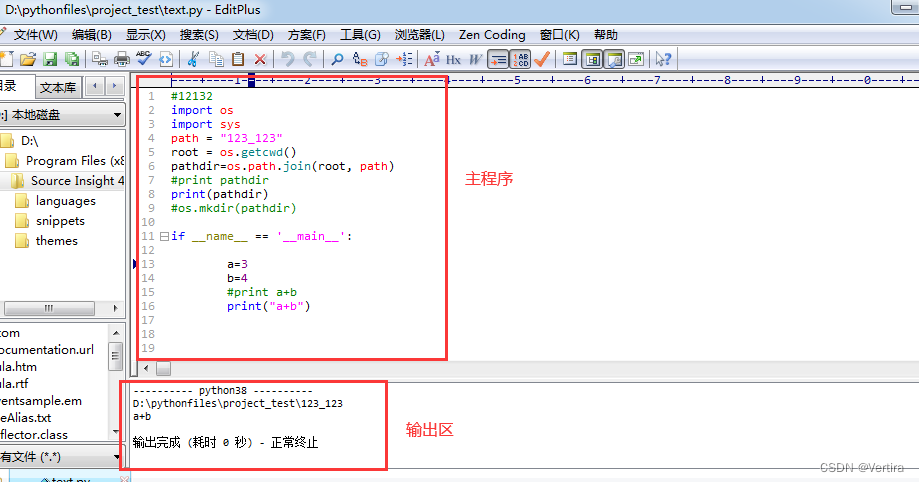
EditPlus 配置python 及Anaconda中的python
若不是pycharm vscode 太大,太占内存,谁会想到用Notepad,EdirPlus 配置python呢!!! 话不多说,首先你自己安装好EditPlus。开始 菜单栏 选择 工具 -> 配置自定义工具 组名:python 命令:d:\*…...

linux 编译 llvm + clang
1. 需要下载以下三个压缩包,下载源码:Release LLVM 15.0.7 llvm/llvm-project GitHub clang-15.0.7.src.tar.xzcmake-15.0.7.src.tar.xzllvm-15.0.7.src.tar.xz 2. 解压后将 clang 源码放入 llvm/tools/ 下 3. 将解压后的 cmake-15.0.7…...
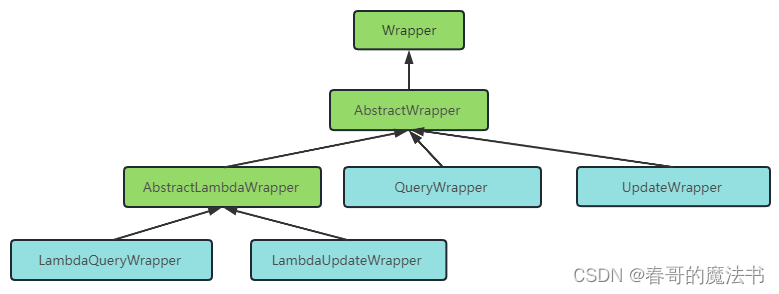
Mybatis 框架 ( 四 ) QueryWrapper
4.5.Wrapper条件构造器 Wrapper : 条件构造抽象类,最顶端父类 AbstractWrapper : 用于查询条件封装,生成 sql 的 where 条件 QueryWrapper : Entity 对象封装操作类,不是用lambda语法 UpdateWrapper &am…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...
