当前位置： 首页 > news >正文

[学习笔记]PageRank算法

news 2025/7/5 2:27:57

参考资料：改变世界的谷歌PageRank算法

pagerank算法用于计算节点重要度

思想

如果网页被更多的入度(被引用)，则网页更重要。
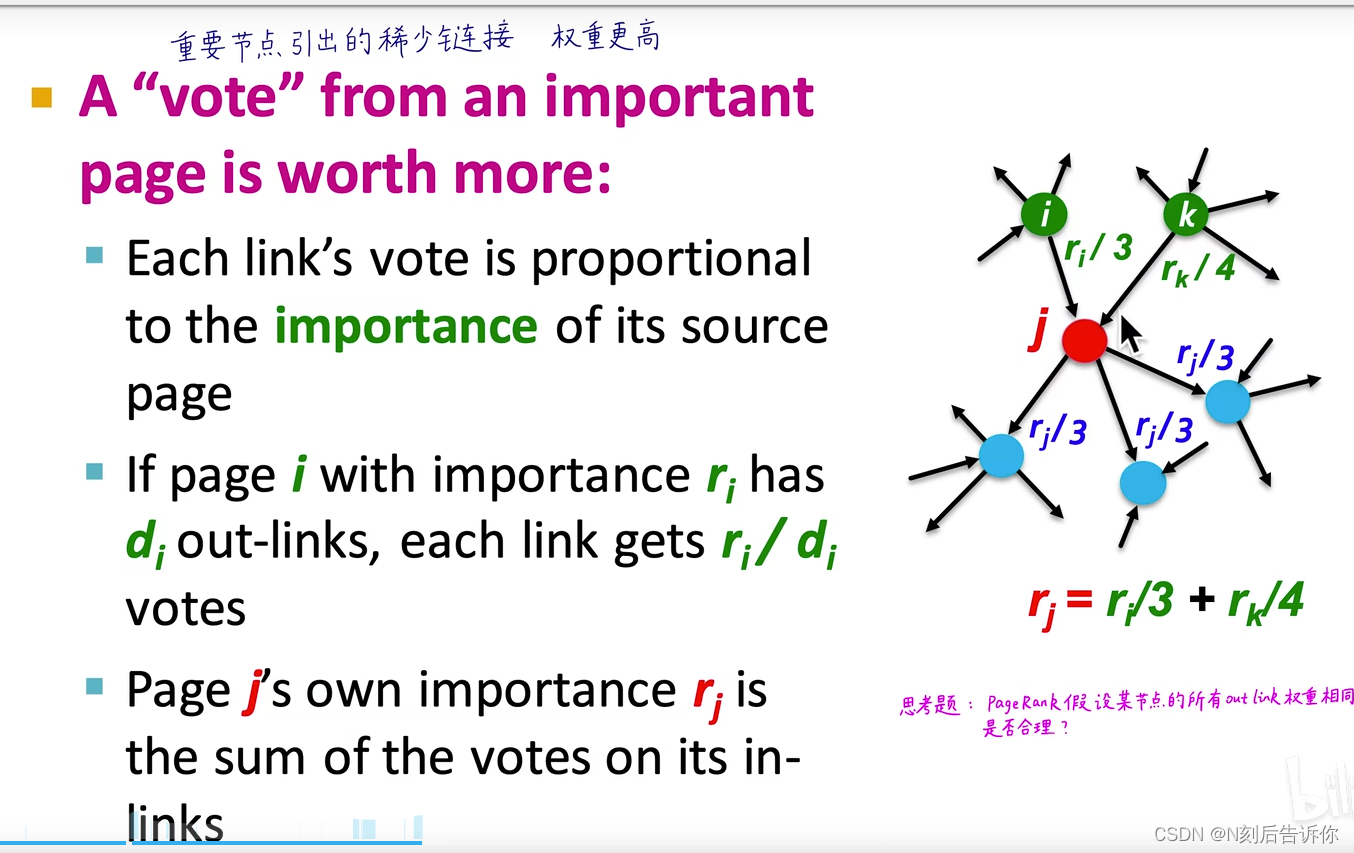
被重要网站引用比被普通网站引用更加凸显重要性。
所以考虑一个网站是否重要，需要看引用它的网站是否重要，这就成了一个递归的问题。

理解pagerank的五个角度

迭代求解线性方程组

在这里插入图片描述

例子

在这里插入图片描述

这里看上去有三个方程，三个未知数，其实只有2个方程。
虽然高斯消元可以求解，但是可扩展性较差。
节点j的rank值 r j r_j rj​是考虑所有到 j j j的节点的rank值，各自除以它的出度，再求和。

迭代求解

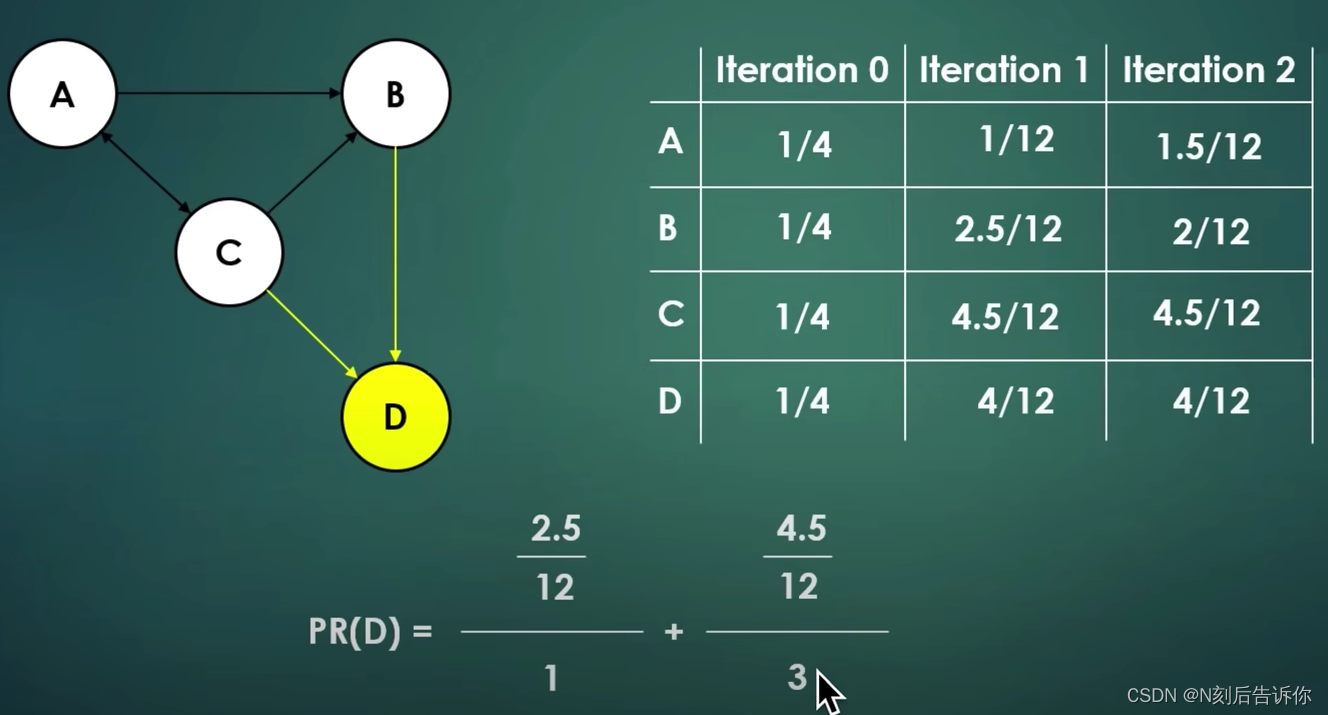
在这里插入图片描述

迭代左乘M矩阵

迭代的过程用矩阵表示：(左边的矩阵的i行j列 A i j 有非零值 A_{ij}有非零值 Aij​有非零值表示存在第j个节点到第i个节点的有向边)
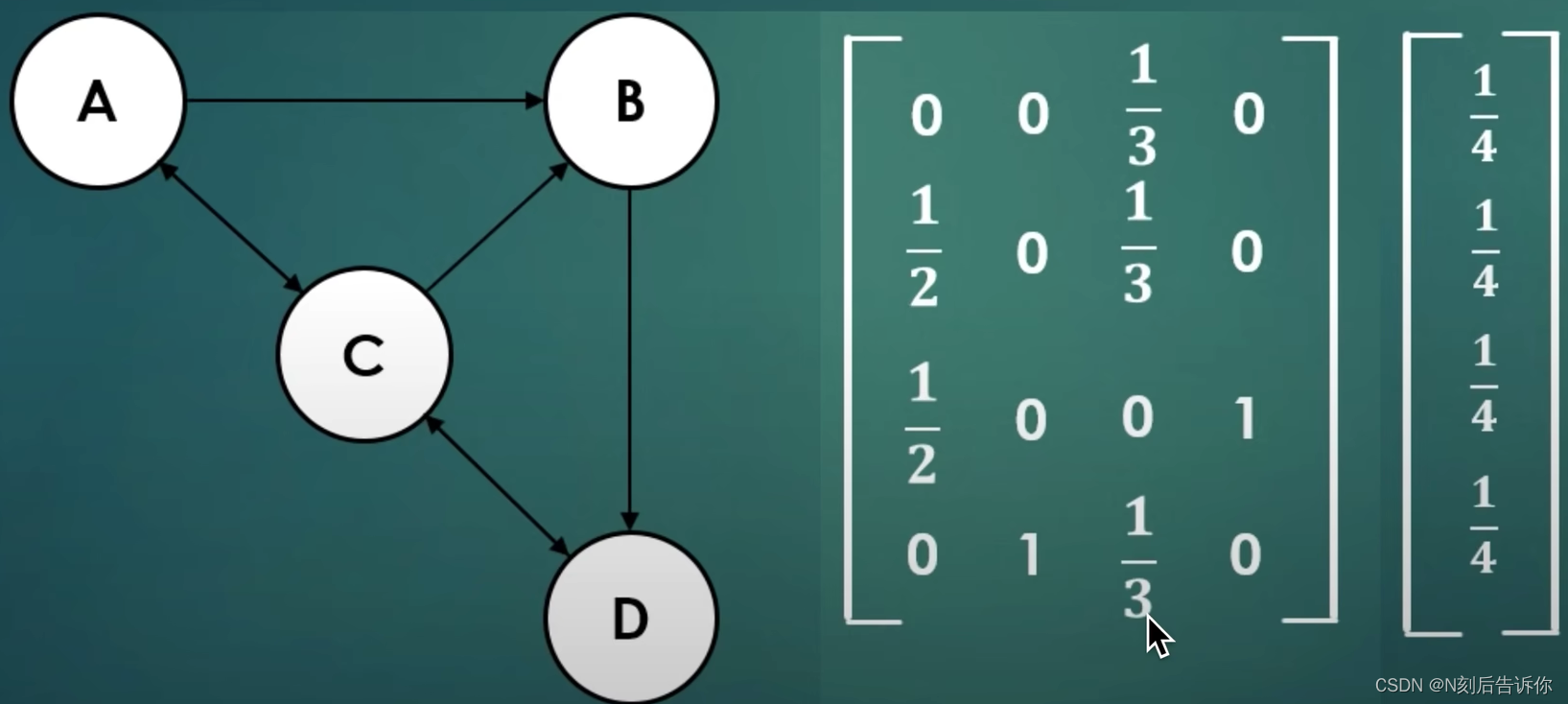
在这里插入图片描述

左边的矩阵称为列概率矩阵(列转移矩阵/列替代矩阵，column stochastic matrix)
右边的向量叫pagerank向量
在这里插入图片描述

矩阵的特征向量

迭代公式：
r = M ⋅ r r=M \cdot r r=M⋅r其实可以看作是
1 ⋅ r = M ⋅ r 1 \cdot r=M \cdot r 1⋅r=M⋅r
从这个角度看，pagerank向量就是M矩阵的特征值为1的特征向量。
在这里插入图片描述

对于Column Stochastic矩阵，由Perreon-Frobenius定理，最大的特征值就是1，且存在唯一的主特征向量(特征值1对应的特征向量)，向量所有元素求和为1。
通过幂迭代的方式，可以快速求解pagerank向量。

随机游走

随机游走->计数求和->归一化为概率，得到的就是pagerank向量。
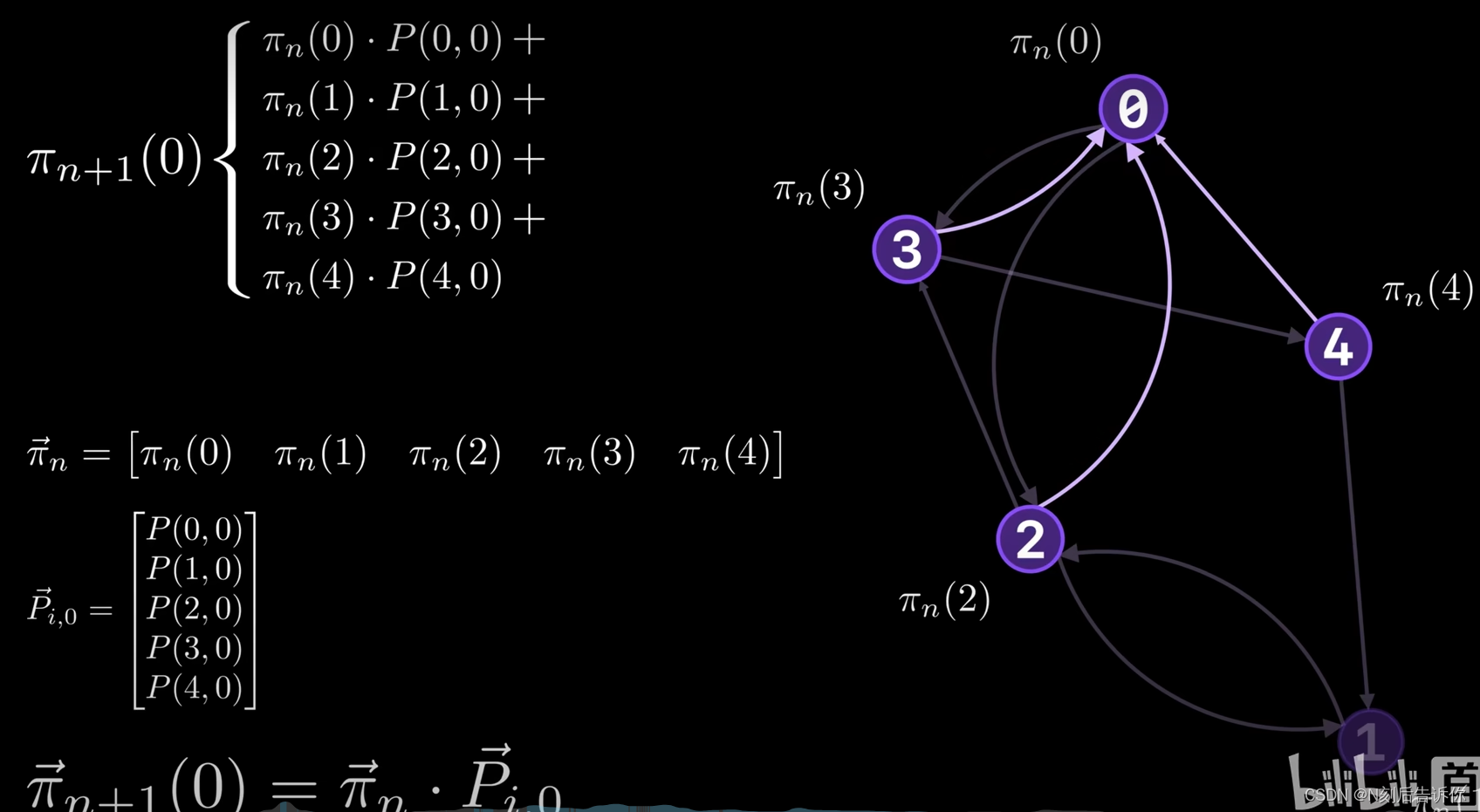
在这里插入图片描述
在这里插入图片描述

马尔科夫链

在这里插入图片描述
在这里插入图片描述

求解pagerank

在这里插入图片描述
在这里插入图片描述

收敛性分析

在这里插入图片描述

1. 是否收敛-收敛，收敛到同一个结果

Ergodic Theorem

根据Ergodic Theorem，对于不可约(irreducible)和非周期(aperiodic)的马尔可夫链：
1.存在一个唯一的稳定的马尔科夫分布
2.并且所有初始分布收敛到同一个分布

可约(reducible)马尔可夫链和不可约马尔可夫链

可约是存在孤立的状态
不可约是所有状态都可达
在这里插入图片描述

周期马尔可夫链和非周期马尔可夫链

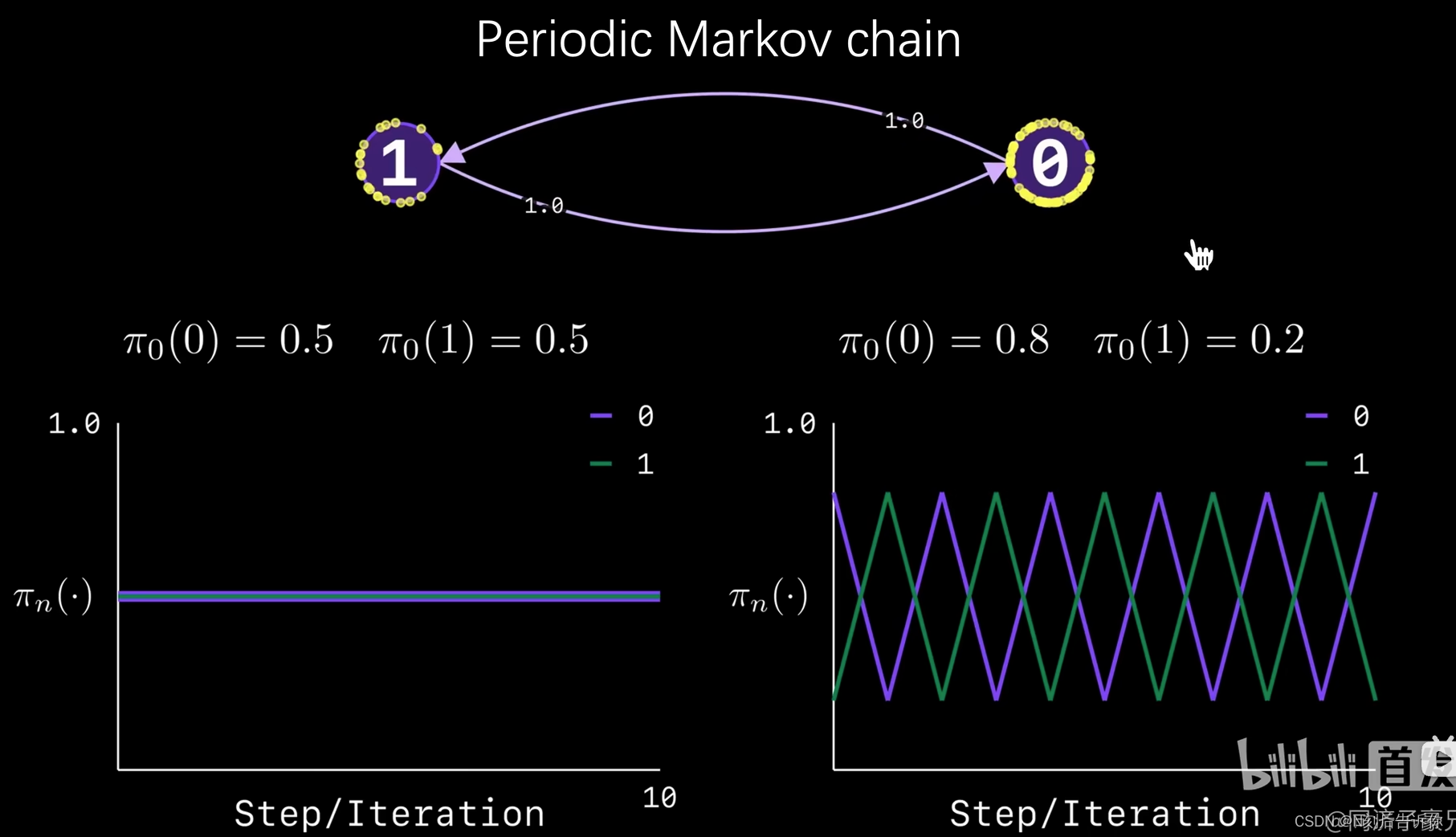
在这里插入图片描述

2.结果是不是代表重要度-两类问题

Spider trap问题

所有的出度边都在group里面，导致这个group吸收了所有的重要度
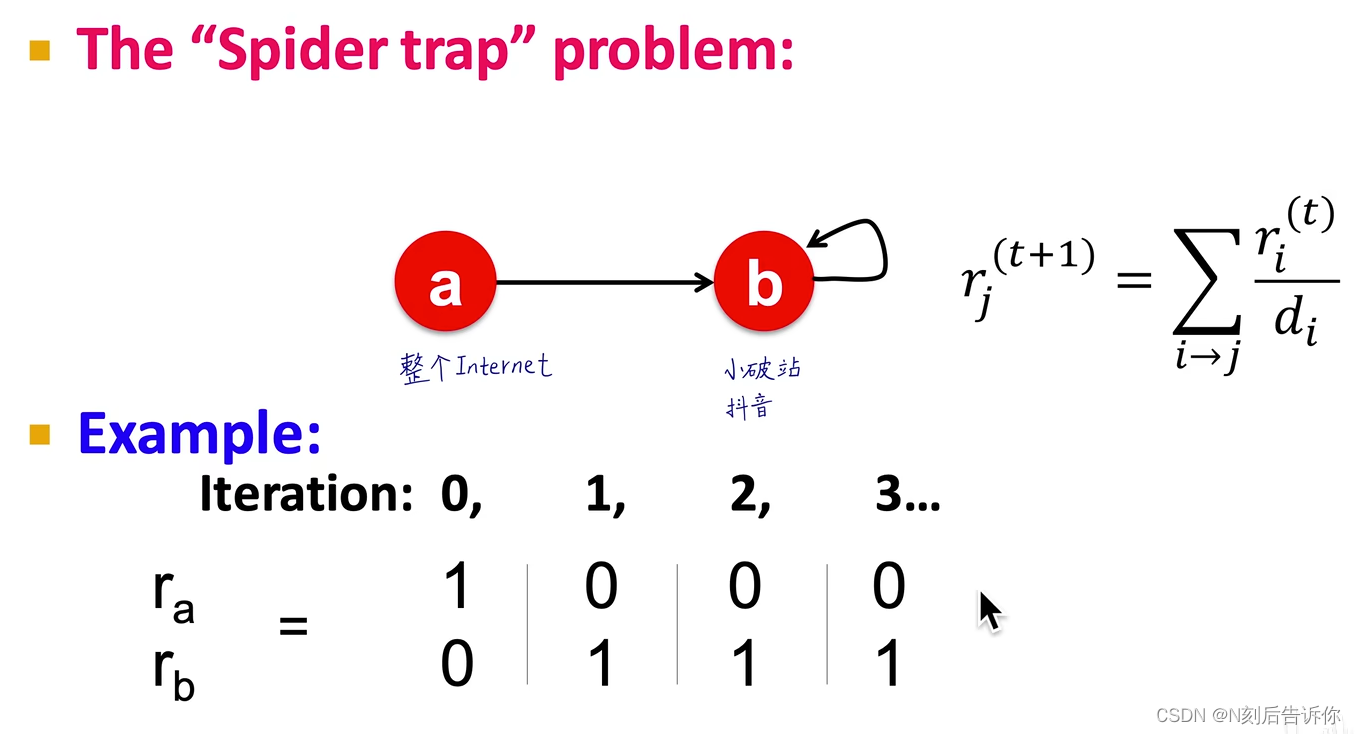
在这里插入图片描述

dead end问题

没有出度，重要度最终为0
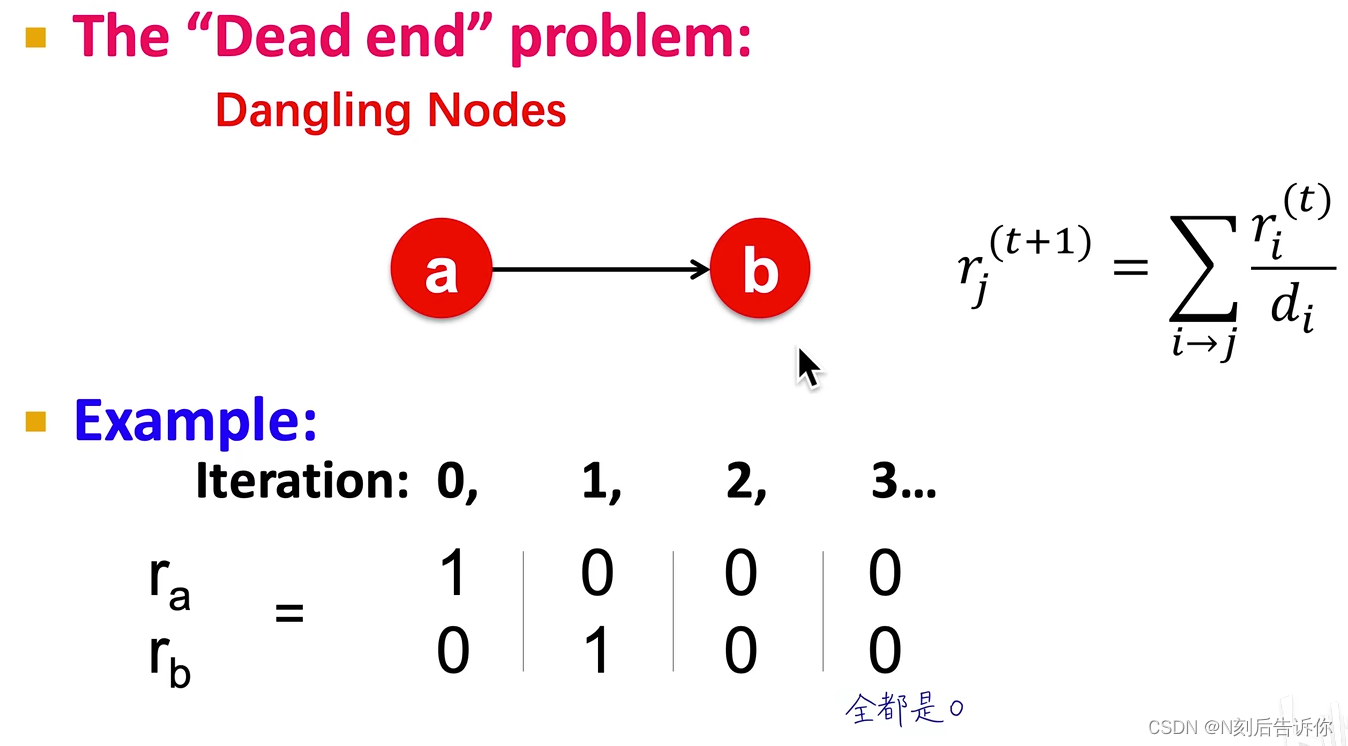
在这里插入图片描述
对于这两种情况，即使收敛了，也不是合理的网络重要度。

例子

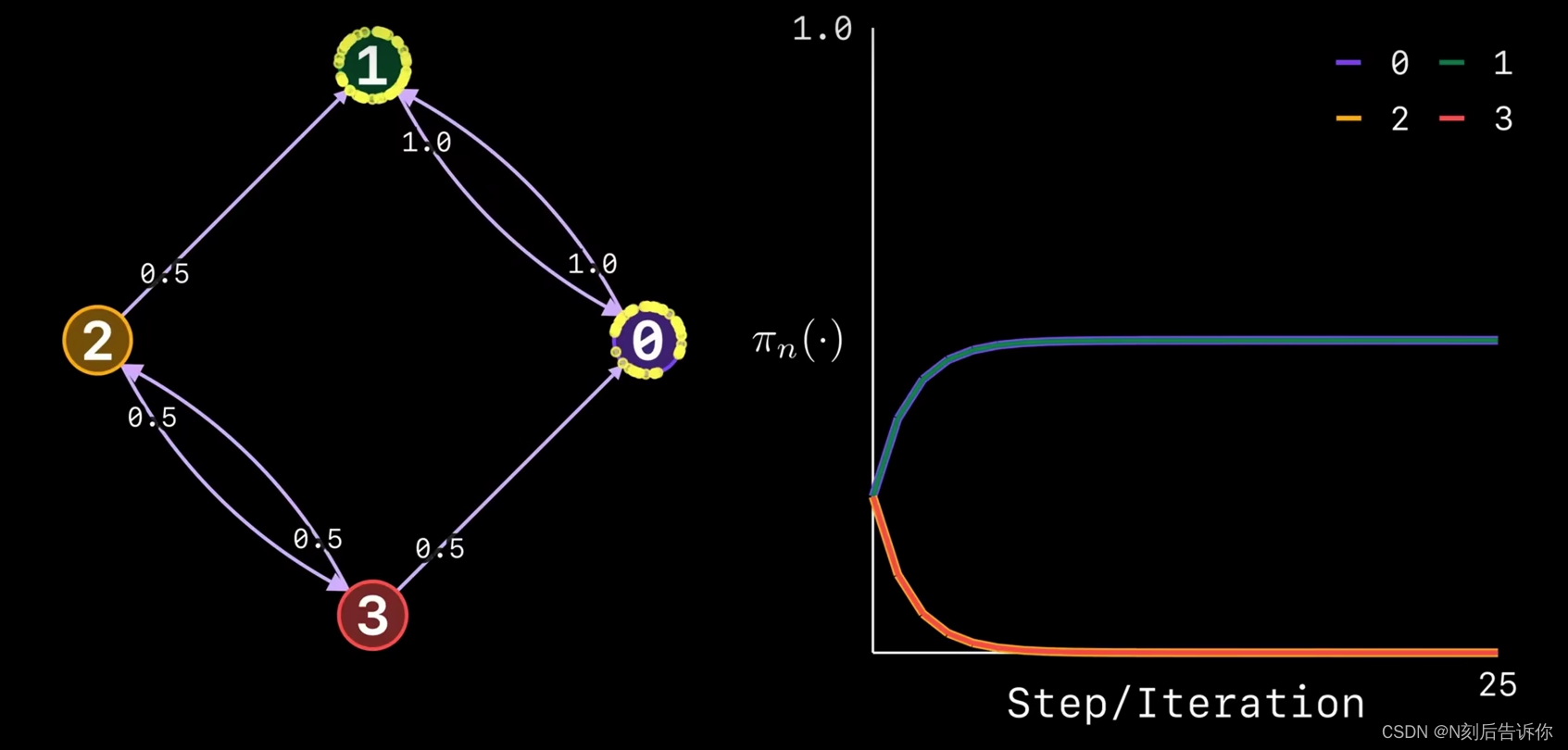
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

解决办法

spider trap问题的解决办法

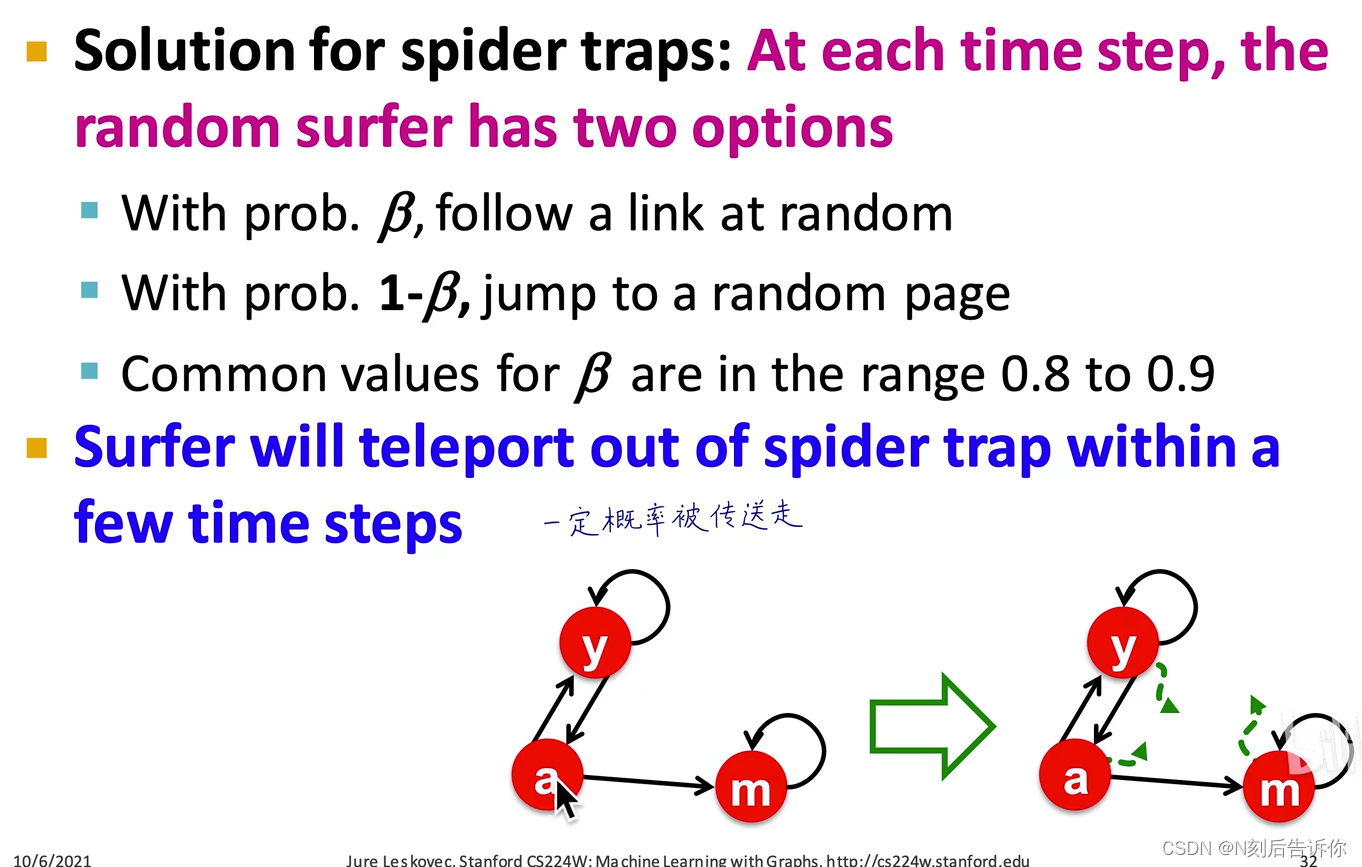
在这里插入图片描述

dead end的解决办法

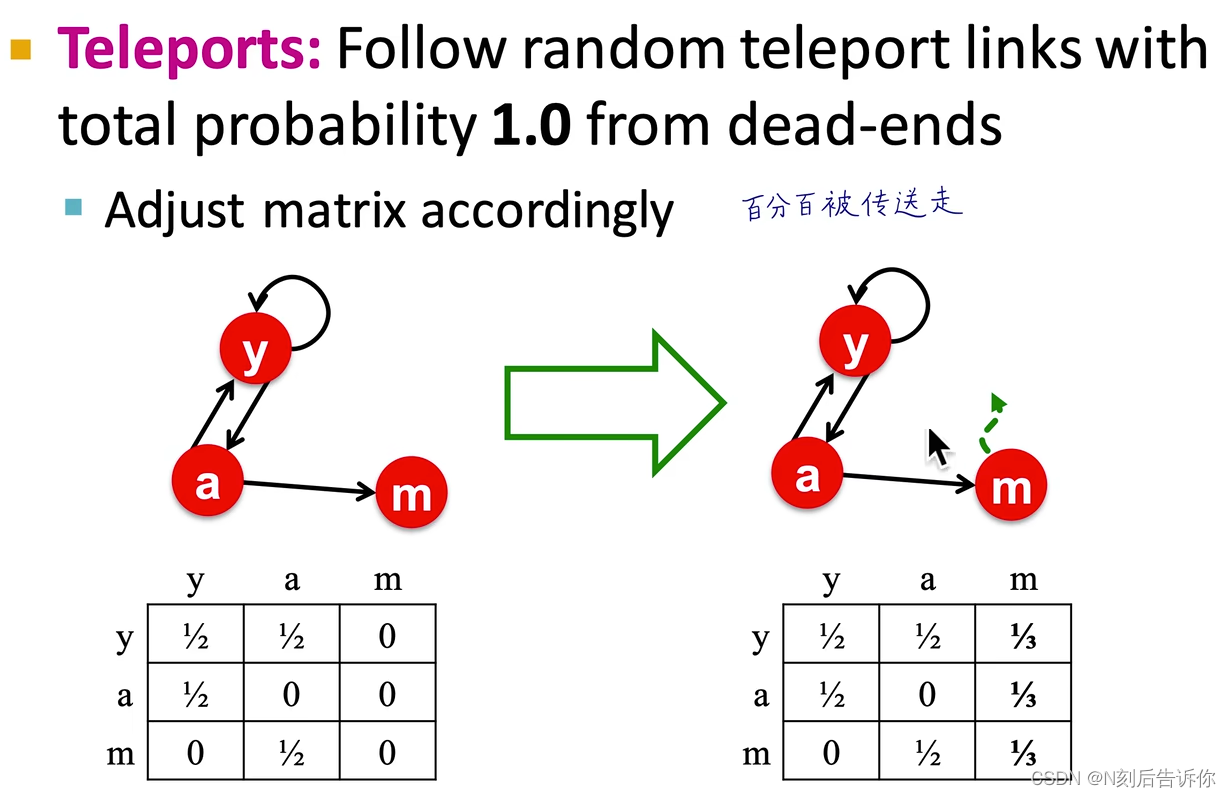
在这里插入图片描述

最终解决办法

在这里插入图片描述
在这里插入图片描述

pagerank的升级-mapreduce的工作

在这里插入图片描述

pagerank算法用于计算节点相似度-用于推荐系统

给定：一个bipartite graph用于表示用户和商品的交互
目标：寻找与指定节点最相似的节点
假设：被同一个用户访问过的节点，更可能是相似的

pagerank，随机游走视角的启发

pagerank的一种解释是：随机游走，并有概率随机传送到网络中的任意一个节点，继续游走
Topic-Specific PageRank(也称为personalized pagerank)：随机游走，并有传送到指定的一些节点，继续游走
random walks with restarts：随机游走，并有传送到指定的一个节点，继续游走

随机游走访问次数-相似性的度量

给定一个节点集query_nodes，模拟一个随机游走：

  • 记录访问次数
  • 在概率 α \alpha α下，在query_nodes中重启walk
  • 有高访问次数的节点则和query_nodes中的点有更高的相似性

伪代码

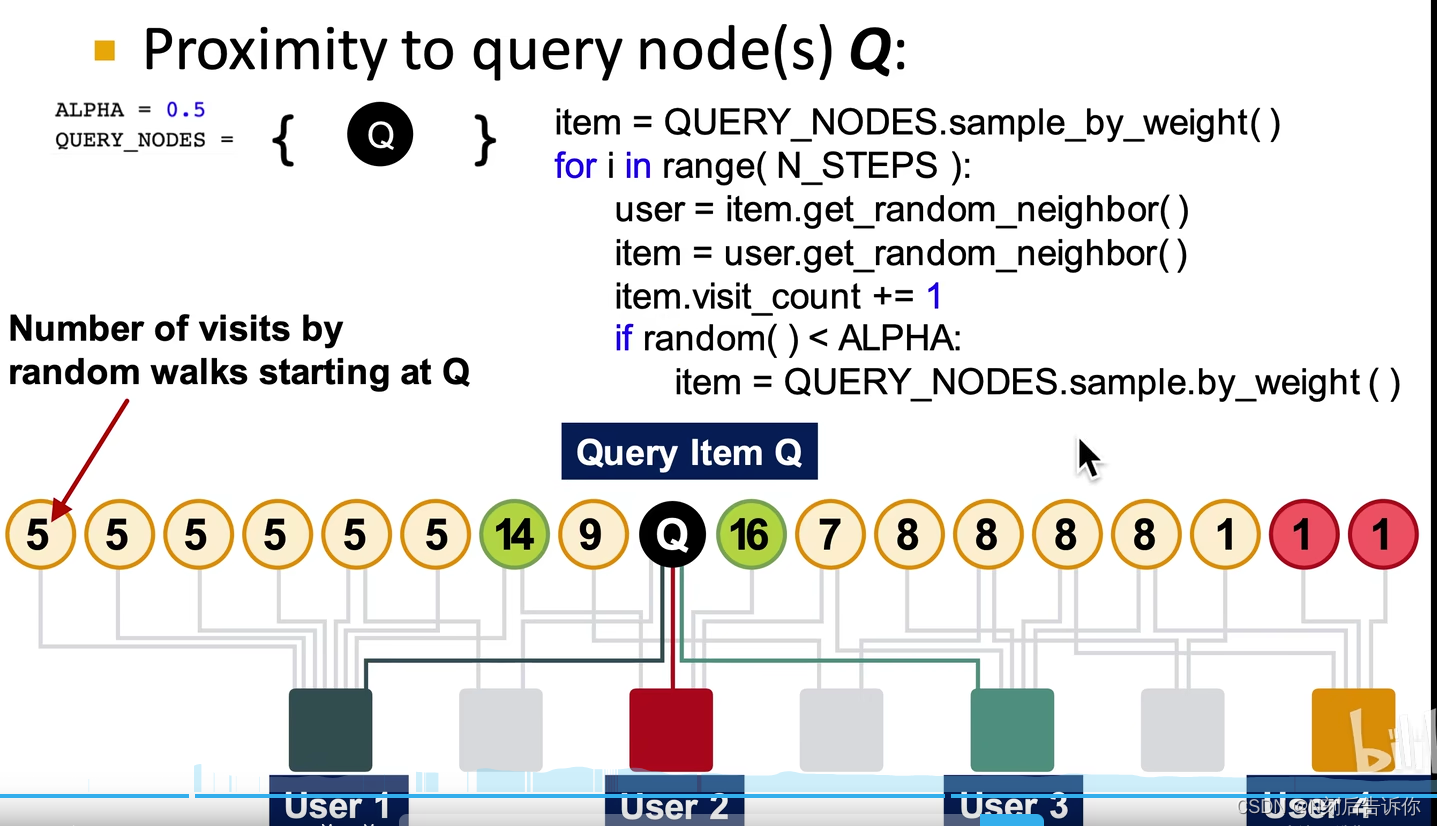
在这里插入图片描述

优点

在这里插入图片描述

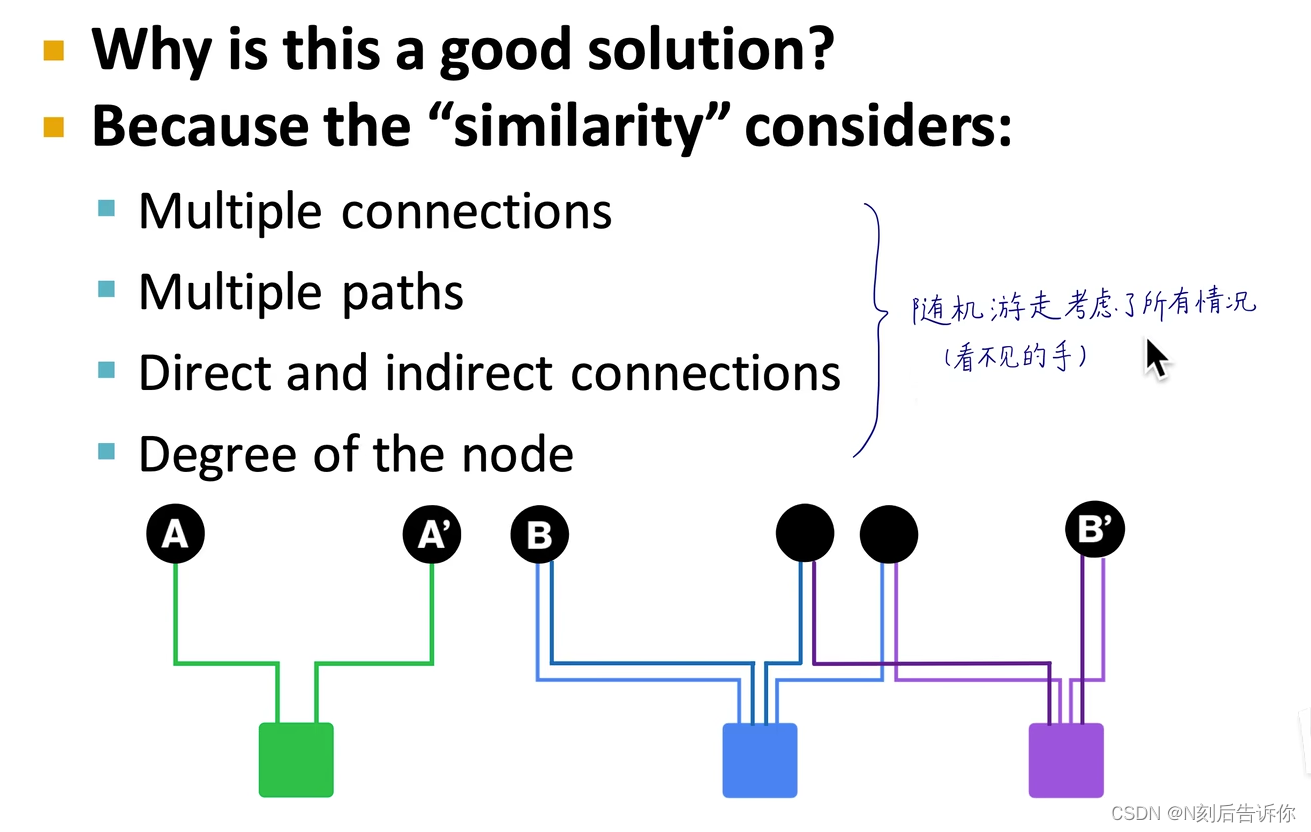
代码实战

参考资料：https://www.bilibili.com/video/BV1Wg411H7Ep/?p=16&spm_id_from=pageDriver

相关文章：

[学习笔记]PageRank算法

参考资料：改变世界的谷歌PageRank算法 pagerank算法用于计算节点重要度 思想 如果网页被更多的入度(被引用)，则网页更重要。 被重要网站引用比被普通网站引用更加凸显重要性。 所以考虑一个网站是否重要，需要看引用它的网站是否重要&#…...

编程日记 2023/9/12 8:31:05

【洛谷算法题】P5704-字母转换【入门1顺序结构】

👨‍💻博客主页：花无缺 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 花无缺 原创 收录于专栏 【洛谷算法题】 文章目录 【洛谷算法题】P5704-字母转换【入门1顺序结构】🌏题目描述🌏输入格式&a…...

编程日记 2023/9/12 8:30:04

Pytorch——查找、替换module相关操作

nn.Module类可用操作 1. model.named_parameters() # 遍历模型的所有参数并打印它们的名称和形状 for name, param in model.named_parameters():print(f"Parameter Name: {name}, Parameter Shape: {param.shape}")输出示例： Parameter Name: conv1.w…...

编程日记 2023/9/12 8:29:03

组件安全以及漏洞复现

组件安全 1. 概述 A9:2017-使⽤含有已知漏洞的组件 A06:2021-Vulnerable and Outdated Components ​ 组件（例如：库、框架和其他软件模块）拥有和应用程序相同的权限。如果应用程序中含有已知漏洞的组件被攻击者利用，可能会造成…...

编程日记 2023/9/12 8:28:02

人工智能安全-4-小样本问题

0 提纲 小样本学习问题数据增强基于模型的小样本学习基于算法的小样本学习相关资源1 小样本学习问题 在小样本监督分类中，通常将问题表述为 N-way-K-shot分类， 当K = 1，称为one-shot learning；当K = 0时，成为zero-shot learning（ZSL）。ZSL就要求学习的问题具备充足的先…...

编程日记 2023/9/12 8:27:01

iOS 17中的Safari配置文件改变了游戏规则，那么如何设置呢

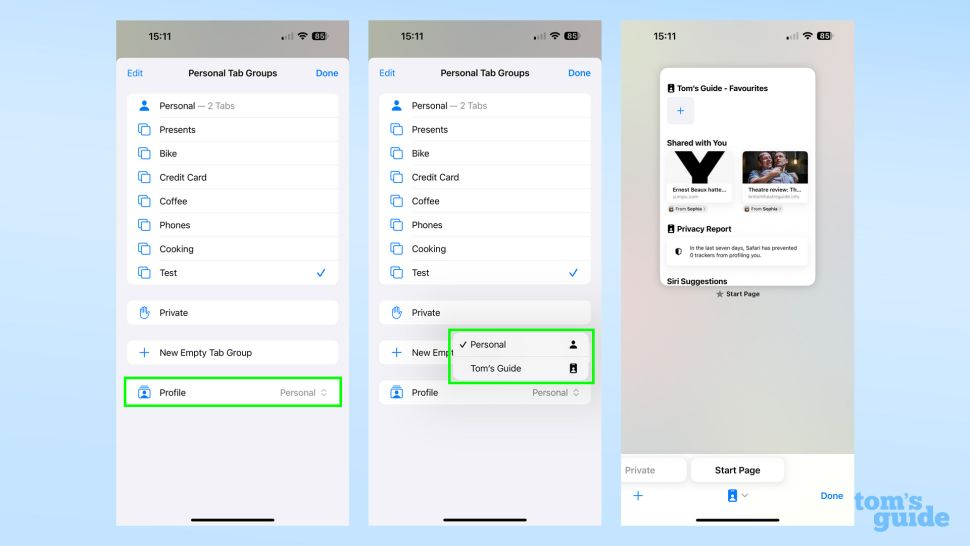
Safari在iOS 17中最大的升级是浏览配置文件——能够在一个应用程序中创建单独的选项卡和书签组。这些也可以跟随你的iPad和Mac，但在本指南中，我们将向你展示如何使用运行iOS 17的iPhone。 你可能有点困惑，为什么Safari中没有明显的位置可以添…...

编程日记 2023/9/12 8:26:01

AC自动机小结

AC自动机是一种多模匹配算法。 常见操作 查询一个串的子串 任何一个串的子串都可以表示成他的一个前缀的后缀 他的前缀可以在Trie树上查询 后缀相当于其在fail树上的所有祖先 例1 ： HDU4117 接上。首先AC自动机要学会离线。 对于每个点查询祖先复杂度很大。…...

编程日记 2023/9/12 8:25:00

【C++】构造函数分类 ③ ( 调用有参构造函数的方法 | 括号法 | 等号法 )

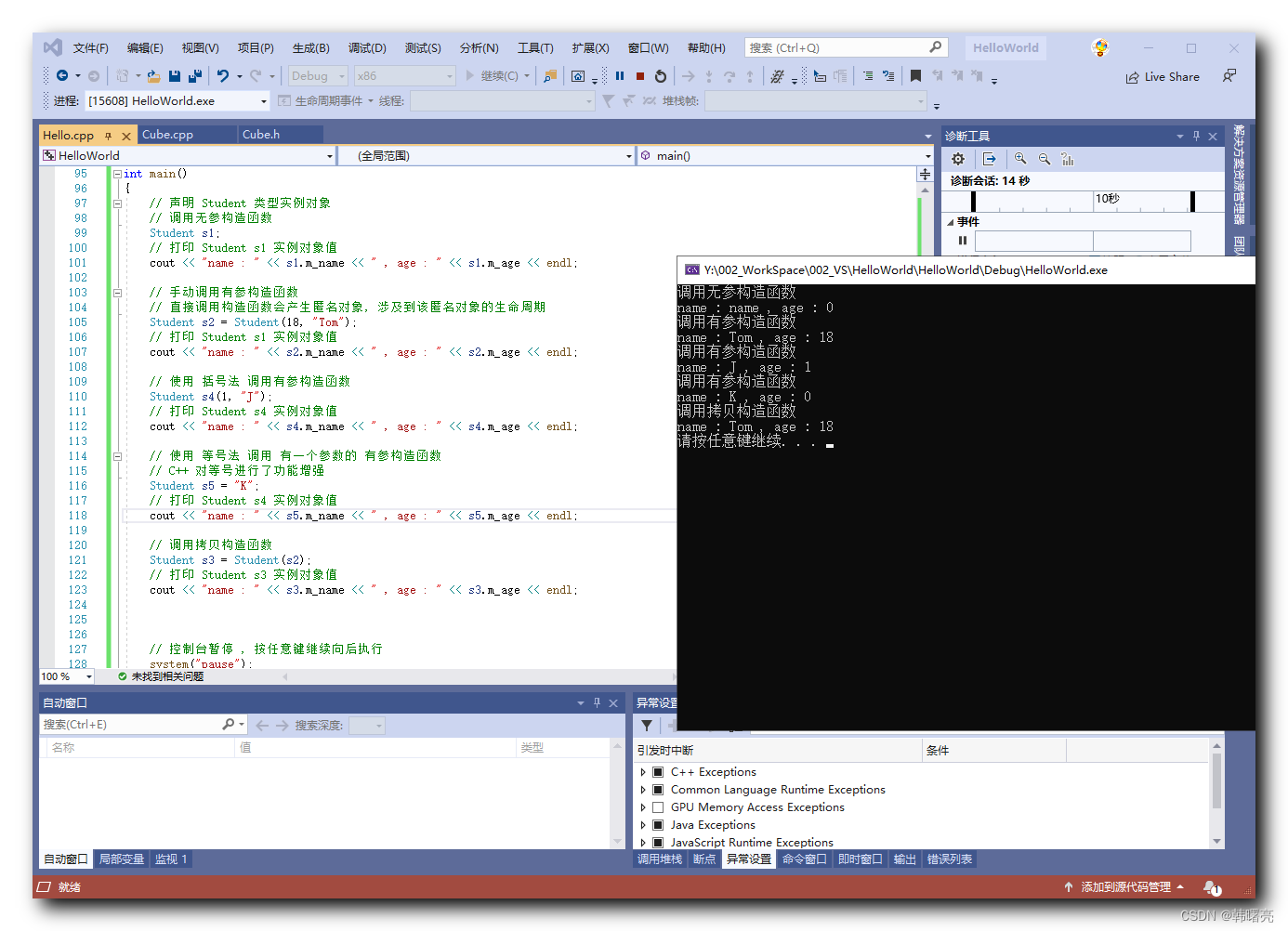
文章目录 一、在不同的内存中创建类的实例对象1、括号法调用构造函数2、等号法调用构造函数 二、完整代码示例 一、在不同的内存中创建类的实例对象 在上一篇博客 【C】构造函数分类 ② ( 在不同的内存中创建类的实例对象 | 栈内存中创建实例对象 | new 关键字创建对象 ) 中 , …...

编程日记 2023/9/12 8:23:59

uni-app 之 uni.request 网络请求API接口

uni-app 之 uni.request 网络请求API接口 image.png <template><!-- vue2的<template>里必须要有一个盒子&#xff0c;不能有两个&#xff0c;这里的盒子就是 view--><view>--- uni.request 网络请求API接口 ---<view><!-- 免费的测试接口 --…...

编程日记 2023/9/12 8:22:56

代码随想录33|509. 斐波那契数，70. 爬楼梯，746. 使用最小花费爬楼梯， 34. 在排序数组中查找元素的第一个和最后一个位置

509. 斐波那契数 链接地址 class Solution { public:int fib(int n) {if (n < 1) return n;vector<int> dp(n 1);dp[0] 0;dp[1] 1;for (int i 2; i < n 1; i) {dp[i] dp[i - 1] dp[i - 2];}return dp[n];} };70. 爬楼梯 链接地址 class Solution { public…...

编程日记 2023/9/12 8:21:55

什么是Executors框架？

Executors 是 Java 标准库中的一个工具类，位于 java.util.concurrent 包中，用于创建和管理线程池。它提供了一组静态工厂方法，用于快速创建不同类型的线程池。Executors 框架的目标是使线程池的创建和管理更加简单和方便。 以下是一些 Executors 框架的常用工厂方法和线程池…...

编程日记 2023/9/12 8:20:54

【kafka】kafka单节点/集群搭建

概述 本章节将分享不同版本的kafka单节点模式和集群模式搭建。 在kafka2.8版本之前&#xff0c;需要依赖zookeeper服务&#xff0c;而在kafka2.8版本&#xff08;包括&#xff09;之后&#xff0c;可以不在依赖zookeeper服务。本章节将分kafka2.8版本之前的版本和之后的版本分…...

编程日记 2023/9/12 8:19:53

如何进行机器学习

进行机器学习主要包含以下步骤&#xff1a; 获取数据&#xff1a;首先需要获取用于学习的数据&#xff0c;数据的质量和数量都会影响机器学习的效果。如果自己的数据量较少&#xff0c;可以尝试在网上寻找公开数据集进行训练&#xff0c;然后使用自己的数据进行微调。另一种方…...

编程日记 2023/9/12 8:18:52

Vue项目使用axios配置请求拦截和响应拦截以及判断请求超时处理提示

哈喽大家好啊&#xff0c;最近做Vue项目看到axios axios官网&#xff1a;起步 | Axios 中文文档 | Axios 中文网 (axios-http.cn)​​​​​​ 重要点&#xff1a; axios是基于Promise封装的 axios能拦截请求和响应 axios能自动转换成json数据 等等 安装&#xff1a; $ npm i…...

编程日记 2023/9/12 8:17:51

《DevOps实践指南》- 读书笔记（四）

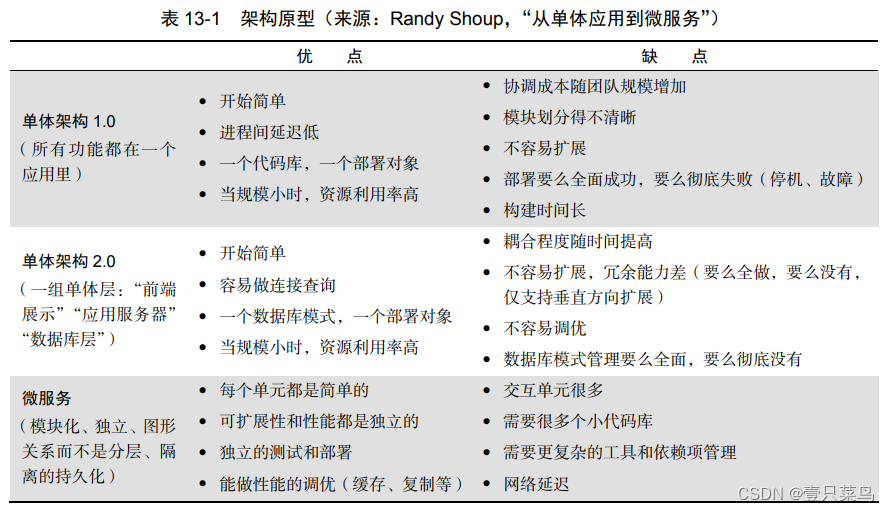
DevOps实践指南 Part 3 第一步 &#xff1a;流动的技术实践11. 应用和实践持续集成11.1 小批量开发与大批量合并11.2 应用基于主干的开发实践11.3 小结 12. 自动化和低风险发布12.1 自动化部署流程12.1.1 应用自动化的自助式部署12.1.2 在部署流水线中集成代码部署 12.2 将部署…...

编程日记 2023/9/12 8:16:51

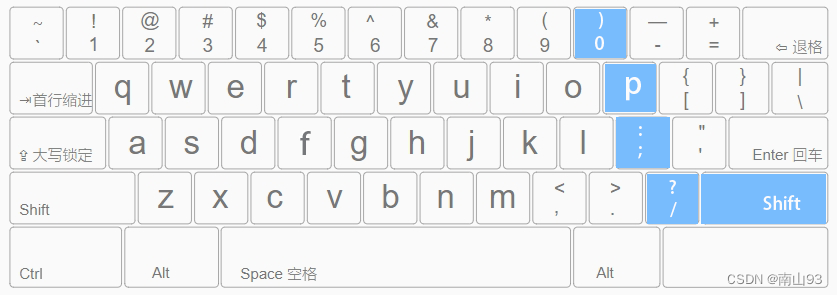
盲打键盘的正确指法指南

简介 很多打字初学者&#xff0c;并不了解打字的正确指法规范&#xff0c;很容易出现只用两根手指交替按压键盘的“二指禅”情况。虽然这样也能实现打字&#xff0c;但是效率极低。本文将简单介绍盲打键盘的正确指法&#xff0c;以便大家在后续的学习和工作中能够提高工作效率…...

编程日记 2023/9/12 8:15:49

【MySQL】索引 详解

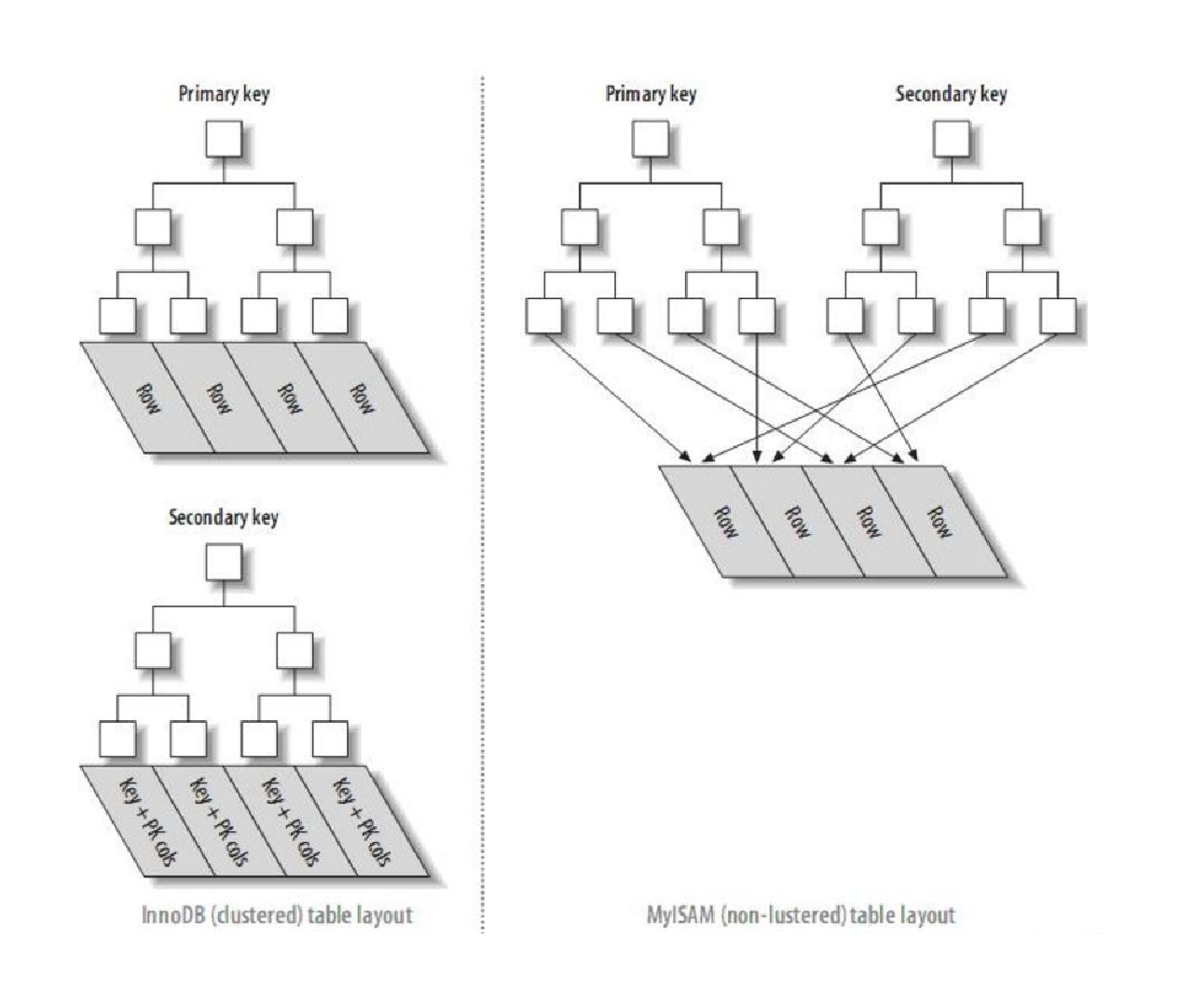
索引 详解 一. 概念二. 作用三. 使用场景四. 操作五. 索引背后的数据结构B-树B树聚簇索引与非聚簇索引 一. 概念 索引是一种特殊的文件&#xff0c;包含着对数据表里所有记录的引用指针。可以对表中的一列或多列创建索引&#xff0c;并指定索引的类型&#xff0c;各类索引有各…...

编程日记 2023/9/12 8:14:47

怎么通过ip地址连接共享打印机

在现代办公环境中&#xff0c;共享打印机已成为一种常见的需求。通过共享打印机&#xff0c;多个用户可以在网络上共享同一台打印机&#xff0c;从而提高工作效率并减少设备成本。下面虎观代理小二二将介绍如何通过IP地址连接共享打印机。 确定打印机的IP地址 首先&#xff0…...

编程日记 2023/9/12 8:13:46

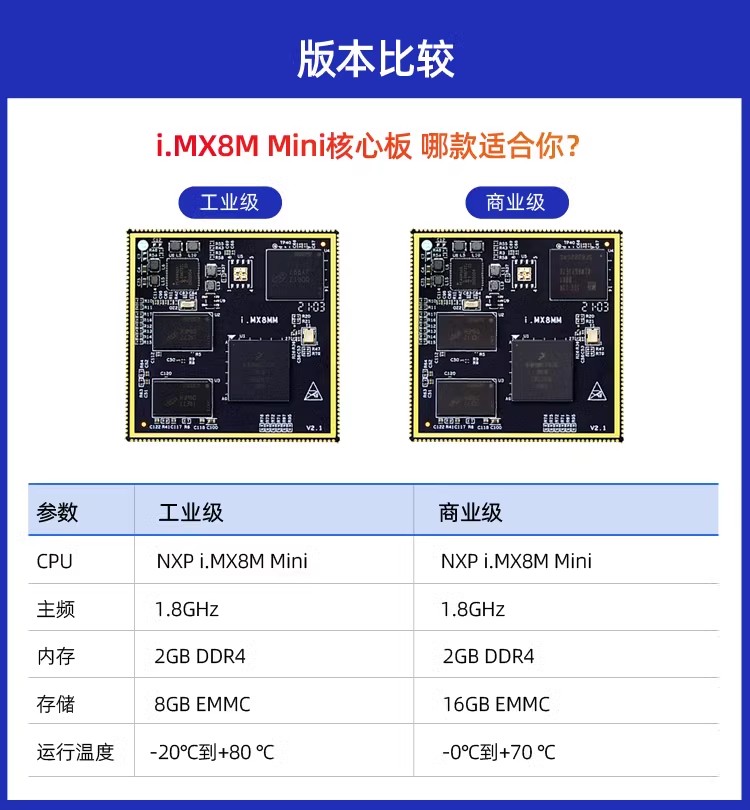
迅为i.MX8mm小尺寸商业级/工业级核心板

尺寸&#xff1a; 50mm*50mm CPU&#xff1a; NXP i.MX8M Mini 主频&#xff1a; 1.8GHz 架构&#xff1a; 四核Cortex-A53&#xff0c;单核Cortex-M4 PMIC&#xff1a; PCA9450A电源管理PCA9450A电源管理NXP全新研制配&#xff0c;iMX8M的电源管理芯片有六个降压稳压器、五…...

编程日记 2023/9/12 8:12:45

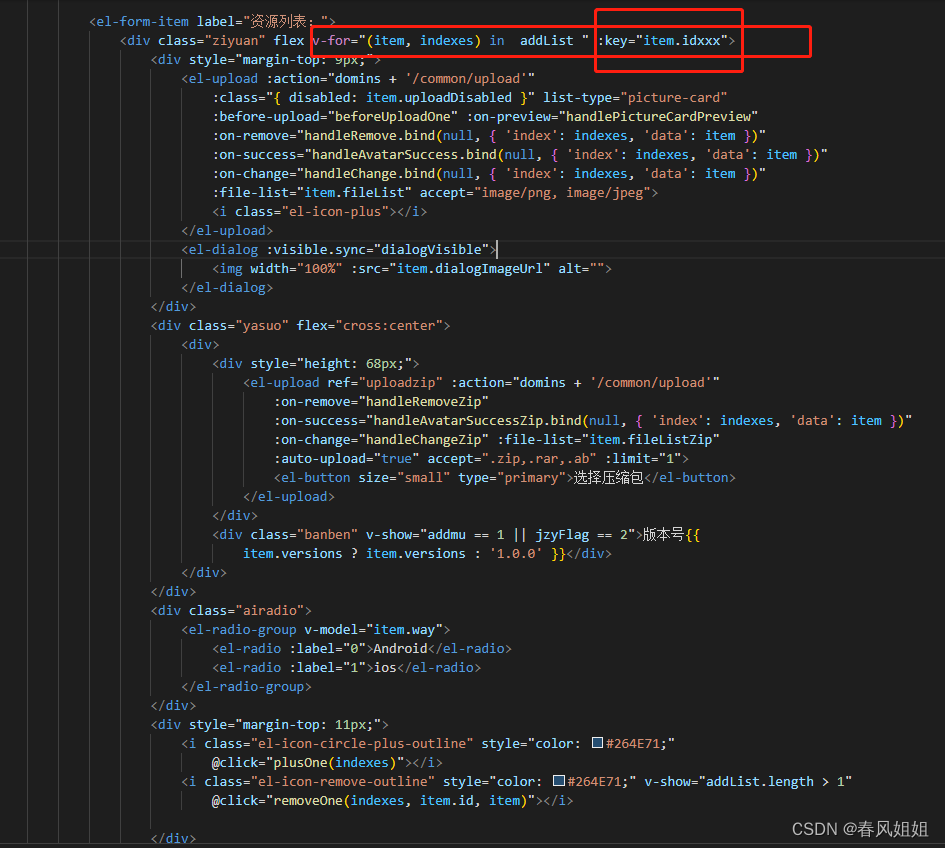
vue中v-for循环数组使用方法中splice删除数组元素（错误：每次都删掉点击的下面的一项）

总结&#xff1a;平常使用v-for的key都是使用index&#xff0c;这里vue官方文档也不推荐&#xff0c;这个时候就出问题了&#xff0c;我们需要key为唯一标识&#xff0c;这里我使用了时间戳&#xff08;new Date().getTime()&#xff09;处理比较复杂的情况&#xff0c; 本文章…...

编程日记 2023/9/12 8:11:44

设计模式和设计原则回顾

设计模式和设计原则回顾 23种设计模式是设计原则的完美体现，设计原则设计原则是设计模式的理论基石， 设计模式 在经典的设计模式分类中（如《设计模式：可复用面向对象软件的基础》一书中），总共有23种设计模式，分为三大类： 一、创建型模式（5种） 1. 单例模式（Sing…...

编程新知 2025/6/20 13:00:49

【WiFi帧结构】

文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成&#xff1a;MAC头部frame bodyFCS&#xff0c;其中MAC是固定格式的&#xff0c;frame body是可变长度。 MAC头部有frame control&#xff0c;duration&#xff0c;address1&#xff0c;address2&#xff0c;addre…...

编程新知 2025/7/4 9:50:55

k8s从入门到放弃之Ingress七层负载

k8s从入门到放弃之Ingress七层负载 在Kubernetes&#xff08;简称K8s&#xff09;中&#xff0c;Ingress是一个API对象&#xff0c;它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress&#xff0c;你可…...

编程新知 2025/6/18 13:47:59

聊聊 Pulsar：Producer 源码解析

一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台&#xff0c;以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中&#xff0c;Producer&#xff08;生产者&#xff09; 是连接客户端应用与消息队列的第一步。生产者…...

编程新知 2025/7/4 10:47:20

Linux简单的操作

ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

编程新知 2025/6/26 2:36:22

Java求职者面试指南：Spring、Spring Boot、MyBatis框架与计算机基础问题解析

Java求职者面试指南&#xff1a;Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问&#xff08;基础概念问题&#xff09; 1. 请解释Spring框架的核心容器是什么&#xff1f;它在Spring中起到什么作用&#xff1f; Spring框架的核心容器是IoC容器&#…...

编程新知 2025/6/16 22:53:40

JS设计模式(4)：观察者模式

JS设计模式(4):观察者模式 一、引入 在开发中&#xff0c;我们经常会遇到这样的场景&#xff1a;一个对象的状态变化需要自动通知其他对象&#xff0c;比如&#xff1a; 电商平台中&#xff0c;商品库存变化时需要通知所有订阅该商品的用户&#xff1b;新闻网站中&#xff0…...

编程新知 2025/6/15 9:27:43

scikit-learn机器学习

# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

编程新知 2025/6/21 5:04:13

[ACTF2020 新生赛]Include 1(php://filter伪协议)

题目 做法 启动靶机&#xff0c;点进去 点进去 查看URL&#xff0c;有 ?fileflag.php说明存在文件包含&#xff0c;原理是php://filter 协议 当它与包含函数结合时&#xff0c;php://filter流会被当作php文件执行。 用php://filter加编码&#xff0c;能让PHP把文件内容…...

编程新知 2025/6/21 18:04:05

解析奥地利 XARION激光超声检测系统：无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用

在工业制造领域&#xff0c;无损检测&#xff08;NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统&#xff0c;以非接触式光学麦克风技术为核心&#xff0c;打破传统检测瓶颈&#xff0c;为半导体、航空航天、汽车制造等行业提供了高灵敏…...

编程新知 2025/7/3 14:36:37