【数据结构】前言概况 - 树
🚩纸上得来终觉浅, 绝知此事要躬行。
🌟主页:June-Frost
🚀专栏:数据结构
🔥该文章针对树形结构作出前言,以保证可以对树初步认知。

目录:
- 🌍前言:
- 🌎树
- ✉️相关概念
- ✉️ 树的存储
- ✉️ 树的应用
- 🌏 二叉树
- ✉️ 特殊二叉树
- ✉️ 二叉树的存储
- ❤️ 结语
🌍前言:
线性结构是一种相对简单的数据结构,元素之间按照一定的顺序排列,每个元素最多有两个接口:前驱和后继。这种结构相对直观,易于理解和管理,类似一种 一对一 的关系。相比之下,树形结构则更为复杂,变为了 一对多 的关系。元素之间的关系不再是简单的线性排列,而是以一个或多个根节点为起点,通过多个分支来连接不同的元素。每个节点可以拥有多个子节点,而且每个子节点可以有任意多的兄弟节点。这种结构需要更多的内存空间来存储元素之间的关系,同时也需要更高级的算法来操作和管理。从复杂性的角度来看,树形结构比线性结构更加复杂。
此外,树的应用广泛,如二叉树、红黑树、B树、哈夫曼树等。在计算机科学中,树的数据结构常常被用于对数据进行组织和存储,以便于高效地实现各种算法和操作。

🌎树
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
①

注意:树是递归定义的,在树的定义中,一个树是由一个根节点和若干个子节点组成的,这些子节点本身也是一棵棵树。因此,树的结构和定义是相互嵌套的。通过递归定义,我们可以将一个树的结构描述为一个递归的过程,即每棵子树又包含着一个根节点和若干个子节点,直到叶节点为止。
⚠树形结构中,子树之间不能有交集,否则会成为 图。
例如:

✉️相关概念
以上图①为例:
-
节点的度:一个节点含有的子树的个数称为该节点的度,如上图:A的为6。
-
叶节点或终端节点:度为0的节点称为叶节点,如上图:B、C、H、I…等节点为叶节点。
-
非终端节点或分支节点:度不为0的节点,如上图:D、E、F、G…等节点为分支节点。
-
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点,如上图:A是B的父节点。
-
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点,如上图:B是A的孩子节点。
-
兄弟节点:具有相同父节点的节点互称为兄弟节点,如上图:B、C是兄弟节点。
-
树的度:一棵树中,最大的节点的度称为树的度,如上图:树的度为6。
-
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推。
-
树的高度或深度:树中节点的最大层次,如上图:树的高度为4
-
堂兄弟节点:双亲在同一层的节点互为堂兄弟,如上图:H、I互为兄弟节点。
-
节点的祖先:从根到该节点所经分支上的所有节点,如上图:A是所有节点的祖先。
-
子孙:以某节点为根的子树中任一节点都称为该节点的子孙,如上图:所有节点都是A的子孙。
-
森林:由m(m>0)棵互不相交的树的集合称为森林。
✉️ 树的存储
树的存储中既要保存值域,也要保存结点和结点之间的关系,有很多存储结构。例如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等

🌟孩子兄弟表示法(LCRS)

🌟双亲表示法
在每一个节点中,存储其父节点的下标。这样就可以将树中各节点的结构关系表示出来,也可以快速地对父节点进行访问。

✉️ 树的应用
树形结构的应用非常广泛。如:
- 数据库中的索引:数据库系统使用树形结构来实现索引,以提高数据访问效率。
- 电子邮件系统:电子邮件系统中的邮件通常是通过树形结构进行组织和管理的,每个邮件可以有多个回复或转发,形成一个树形结构。
- 编译器中的语法树:编译器将源代码解析为语法树,其中每个节点表示特定的语法结构,如一个函数、一个循环或一个条件语句。
- 文件系统的目录树结构。

在实践当中,用的最多的树是二叉树。
🌏 二叉树
一棵二叉树是结点的一个有限集合,该集合可以为空,也可以由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
对于任意的二叉树都是由以下几种情况复合而成的:

例如:

注意:
- 二叉树不存在度大于2的结点
- 由于二叉树最多有2个孩子,为了区分概念,就定义了左孩子和右孩子,所以二叉树的子树有左右之分,次序不能颠倒 —— 二叉树是有序树。
✉️ 特殊二叉树
🌟满二叉树
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。如果一个满二叉树的层数为K,结点总数就是2h-1,同样的,如果一个满二叉树的节点总数为N,则层数为log2(N+1)。
🌟满二叉树
假设有h层,前h-1层都是满的,最后一层不一定满,节点从左到右连续。要注意的是满二叉树是一种特殊的完全二叉树。假设有h层,则完全二叉树的节点范围为 [ 2(h-1) , 2h - 1] 。
🌟一些性质:
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2(i-1)个结点.
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2h-1.
- 对任何一棵二叉树, 如果度为0的其叶结点个数为n0, 度为2的分支结点个数为n2 ,则有 n0= n2+1
✉️ 二叉树的存储
二叉树的存储结构通常可以采用顺序存储和链式存储两种。
- 链式存储:对于一般的二叉树,通常采用链式存储方式。每个节点包含三个字段:数据域、左孩子指针和右孩子指针。数据域用于存储节点的值,左孩子指针指向该节点的左子节点,右孩子指针指向该节点的右子节点。如果某个节点没有子节点,对应的指针就为空(NULL)。
- 顺序存储:对于完全二叉树,可以直接使用数组进行存储,将根节点存储在索引为1的位置,然后按照层次顺序从左到右,从上到下,对每个节点赋予一个唯一的索引。这种存储方式对于完全二叉树来说,可以节省存储空间,并且可以通过索引快速访问节点。
📚顺序存储结构和链式存储结构各有优劣,需要根据实际应用场景和需求来选择使用哪种存储方式。如果需要频繁查找且表的长度变化不大,可以使用顺序存储结构;如果需要频繁插入和删除操作且表的长度变化较大,使用链式存储结构可能会更好。
❤️ 结语
文章到这里就结束了,如果对你有帮助,你的点赞将会是我的最大动力,如果大家有什么问题或者不同的见解,欢迎大家的留言~
相关文章:

【数据结构】前言概况 - 树
🚩纸上得来终觉浅, 绝知此事要躬行。 🌟主页:June-Frost 🚀专栏:数据结构 🔥该文章针对树形结构作出前言,以保证可以对树初步认知。 目录: 🌍前言:dz…...
MySQL——事务
一、事务的开始与结束 一个数据库事务由一条或多条sql语句构成,它们形成一个逻辑的工作单元。这些sql语句要么全部执行成功,要么全部执行失败。 1.1.事物的开始 1.对于DDL(create,alter,drop)和DCL&…...
虚拟机Ubuntu操作系统最基本终端命令(安装包+详细解释+详细演示)
虚拟机及乌班图(Ubuntu操作系统) 提示:大家需要软件的可以直接在此链接中提取 链接:https://pan.baidu.com/s/1_4VHGTlXjIuVhBINeOuBCA 提取码:nd0c 文章目录 虚拟机及乌班图(Ubuntu操作系统)终…...

Android 11.0 当系统内置两个Launcher时默认设置Launcher3以外的那个Launcher为默认Launcher
1.概述 在11.0定制化开发中,由于产品开发需要要求系统内置两个Launcher,一个是Launcher3,一个是自己开发的Launcher,当系统启动Launcher时, 不要弹出Launcher选择列表 选择哪个Launcher要求默认选择自己开发的Launcher作为默认Launcher,关于选择Launcher列表 其实都是在Res…...

NO5.心愿打印机
def light():#定义一个函数,以:结尾print(红灯2)#打印print(绿灯3)#打印 print(黄灯1)#和def顶格,先执行 light()#调用light函数【PDF转Word】 https://fzqxk86ywz.feishu.cn/sheets/GugIsI9zKhNaEwtJscbcgKFCn6b 【Fiddler汉化】 https://fzqxk86ywz.f…...

cudart.so vs cuda.so的区别
libcuda.so provides access to the CUDA driver API, whereas libcudart.so provides access to the CUDA runtime API. libcuda.so提供对CUDA驱动程序API的访问,而libcuart.so提供了对CUDA运行时API的访问。 在wsl中cuda.so位于/usr/lib/wsl/lib/libcuda.so 可以…...

Oracle集群管理-19C集群禁用numa和大页内存特性
Linux Redhat 7.9关闭内存管理特性 1 关闭大页内存 [rootdb1 ~]# cat /sys/kernel/mm/transparent_hugepage/defrag [always] madvise never [rootdb1 ~]# cat /sys/kernel/mm/transparent_hugepage/enabled [always] madvise never echo never > /sys/kernel/mm/transpare…...

题目:2726.使用方法链的计算器
题目来源: leetcode题目,网址:2726. 使用方法链的计算器 - 力扣(LeetCode) 解题思路: 按要求模拟,在计算后返回自己以达到链式调用的目的。 解题代码: class Calculator {/**…...

基于ASP.NET的驾校管理系统设计与实现
摘 要 伴随国民经济的飞速发展和人民生活水平的不断提高,家用汽车在我国逐渐普及。面对不断增长的庞大的用户群,随之产生的驾驶培训行业,规模不断扩大。近年来,随着Internet的迅速发展以及网页制作技术的日臻完善,驾校…...

第一章 计算机系统概述 三、操作系统的发展与分类
一、手工操作阶段 缺点:人机速度矛盾 二、批处理阶段 1、单道批处理系统(引入脱机输入输出技术) 优点:缓解人机速度矛盾 缺点:资源利用率依然很低 2、多道批处理系统(操作系统开始出现) 优点:多道程序并发进行,…...
【2023年11月第四版教材】第12章《质量管理》(第二部分)
第12章《质量管理》(第二部分) 4 规划质量管理4.1 数据收集★★★4.2 数据分析★★★4.3 数据表现★★★4.4 质量管理计划★★★4.5 质量测量指标★★★ (22下35) 4 规划质量管理 组过程输入工具和技术输出计划1.规划质量管理1.项…...

metinfo __ 6.0.0 __ file-read
metinfo __ 6.0.0 __ file-read 说明内容漏洞编号–漏洞名称MetInfo 6.0.0 任意文件读取漏洞漏洞评级高危影响范围6.0.0.0漏洞描述MetInfo 存在任意文件读取漏洞,攻击者利用该漏洞,在具有权限的情况下,可以读取网站任意文件,包括…...
打造高效的私密论坛网站:Cpolar内网穿透+HadSky轻量级搭建指南
文章目录 前言1. 网站搭建1.1 网页下载和安装1.2 网页测试1.3 cpolar的安装和注册 2. 本地网页发布2.1 Cpolar临时数据隧道2.2 Cpolar稳定隧道(云端设置)2.3 Cpolar稳定隧道(本地设置)2.4 公网访问测试 总结 前言 经过多年的基础…...
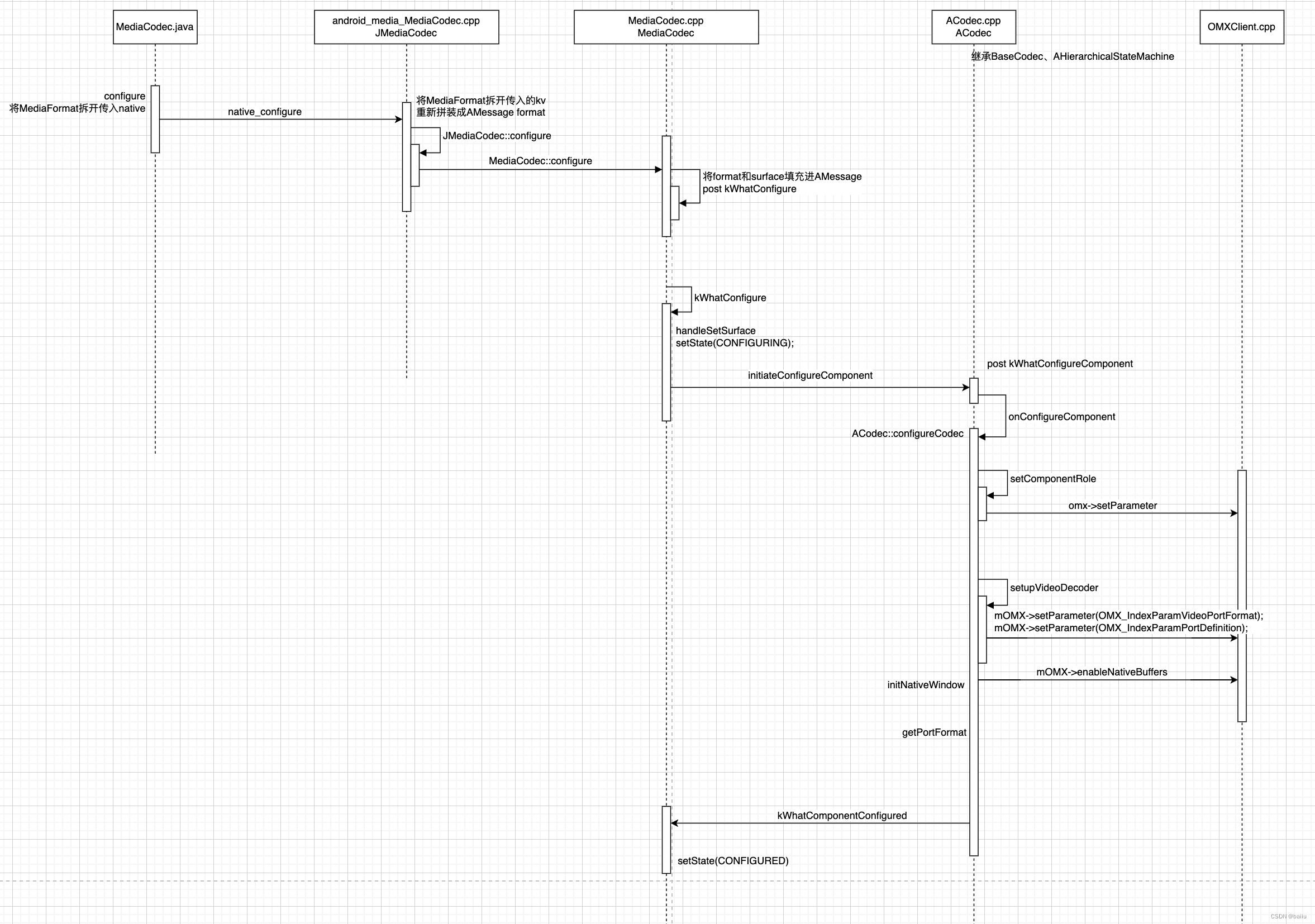
MediaCodec源码分析 configure流程
前言 本文梳理MediaCodec configure流程,基于7.0代码,这里只分析AVC和HEVC的视频硬解,流程图如下。 代码见: frameworks/base/media/java/android/media/MediaCodec.java frameworks/base/media/jni/android_media_MediaCodec.h frameworks/base/media/jni/android_media_…...
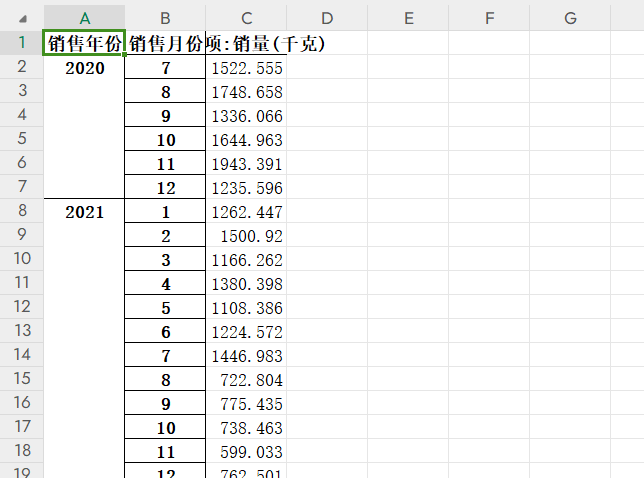
借助ChatGPT使用Pandas实现Excel数据汇总
一、问题的提出 现在有如下一个Excel表: 上述Excel表中8万多条数据,记录的都是三年以来花菜类的销量,现在要求按月汇总实现统计每个月花菜类的销量总和,如果使用Python的话要给出代码。 二、问题的解决 1.首先可以用透视表的方…...
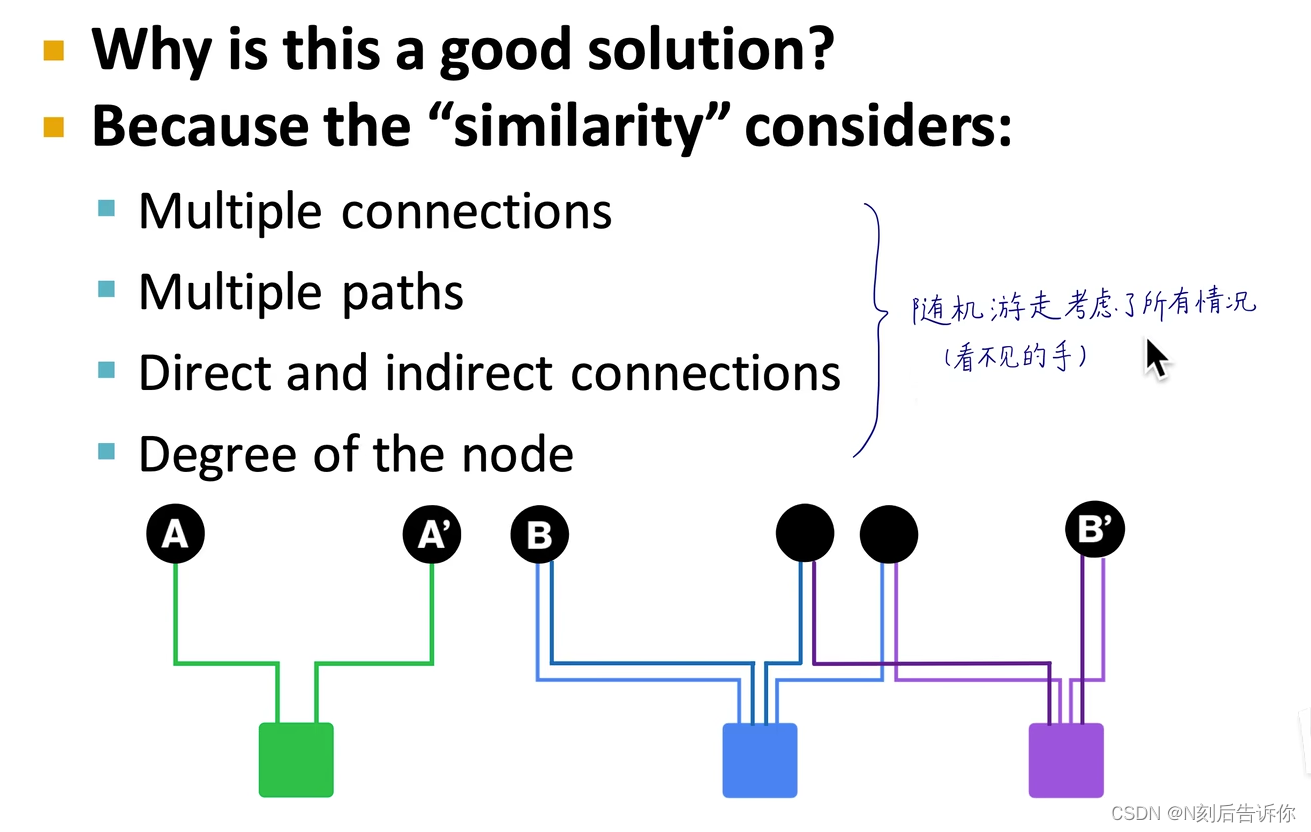
[学习笔记]PageRank算法
参考资料:改变世界的谷歌PageRank算法 pagerank算法用于计算节点重要度 思想 如果网页被更多的入度(被引用),则网页更重要。 被重要网站引用比被普通网站引用更加凸显重要性。 所以考虑一个网站是否重要,需要看引用它的网站是否重要&#…...

【洛谷算法题】P5704-字母转换【入门1顺序结构】
👨💻博客主页:花无缺 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 花无缺 原创 收录于专栏 【洛谷算法题】 文章目录 【洛谷算法题】P5704-字母转换【入门1顺序结构】🌏题目描述🌏输入格式&a…...

Pytorch——查找、替换module相关操作
nn.Module类可用操作 1. model.named_parameters() # 遍历模型的所有参数并打印它们的名称和形状 for name, param in model.named_parameters():print(f"Parameter Name: {name}, Parameter Shape: {param.shape}")输出示例: Parameter Name: conv1.w…...
组件安全以及漏洞复现
组件安全 1. 概述 A9:2017-使⽤含有已知漏洞的组件 A06:2021-Vulnerable and Outdated Components 组件(例如:库、框架和其他软件模块)拥有和应用程序相同的权限。如果应用程序中含有已知漏洞的组件被攻击者利用,可能会造成…...

人工智能安全-4-小样本问题
0 提纲 小样本学习问题数据增强基于模型的小样本学习基于算法的小样本学习相关资源1 小样本学习问题 在小样本监督分类中,通常将问题表述为 N-way-K-shot分类, 当K = 1,称为one-shot learning;当K = 0时,成为zero-shot learning(ZSL)。ZSL就要求学习的问题具备充足的先…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
