【数据结构】树和二叉树概念
1.树概念及结构
树概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。

- 有一个特殊的结点,称为根结点,根节点没有前驱结点
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 因此,树是递归定义的。
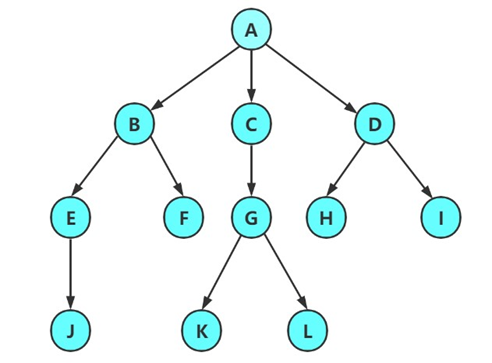
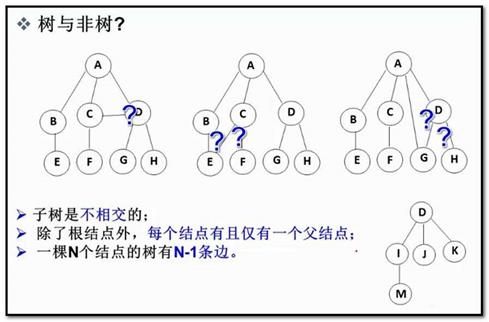
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
树的相关概念
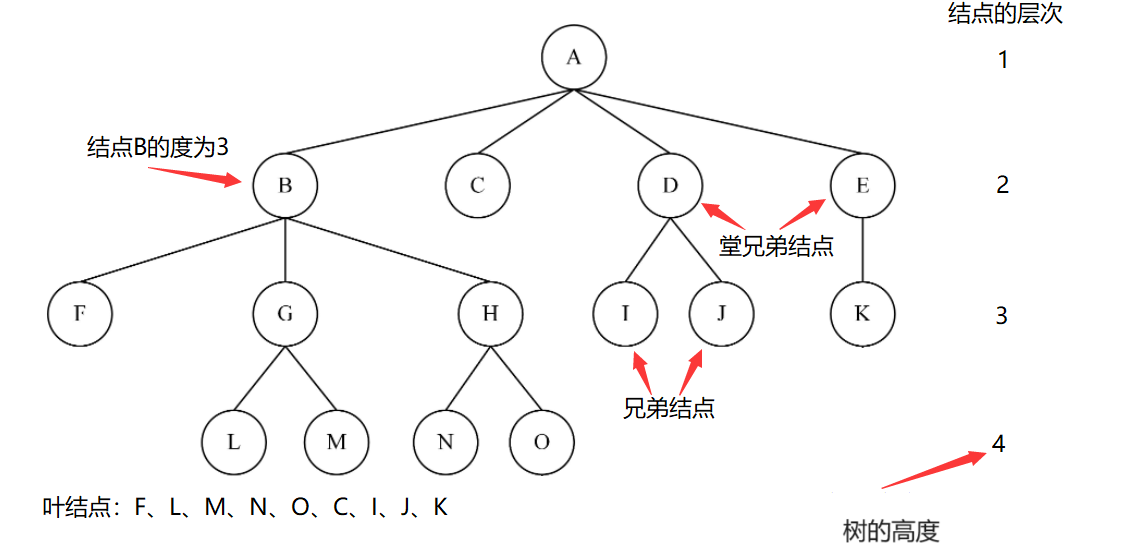
- 结点的度:一个结点含有的子树的个数称为该结点的度。
- 叶结点(终端结点):度为0的结点称为叶结点。
- 非终端结点(分支结点):度不为0的结点。
- 父结点(双亲结点):若一个结点含有子结点,则这个结点称为其子结点的父结点。
- 子结点(孩子结点):一个结点含有的子树的根结点称为该结点的子结点。
- 兄弟结点:具有相同父结点的结点互称为兄弟结点。
- 树的度:一棵树中,最大的结点的度称为树的度。
- 结点的层次:从根开始定义起,根为第一层,根的子结点为第二层,以此类推。
- 树的高度(树的深度):树中结点的最大层次。
- 堂兄弟结点:双亲在同一层的结点互称为堂兄弟结点。
- 结点的祖先:从根到该结点所经分支上的所有结点。
- 子孙:以某结点为根的子树中任一结点都称为该结点的子孙。
- 森林:由m(m>0)棵互不相交的树组成的集合称为森林。
树的表示
树结构相对于线性表就比较复杂了,要存储和表示起来就比较麻烦了,实际中树有很多种表示方法。如:双亲表示法、孩子表示法、孩子兄弟表示法等等。其中最常用的是孩子兄弟表示法。
孩子兄弟表示法中,所定义的结点类型大致是这样的:
typedef int DataTypestruct Node{struct Node* firstChild; //第一个孩子结点struct Node* nextBrother; //指向下一个兄弟结点DataType data; //结点中的数据域
};
对于任意树,我们都可以用孩子兄弟法访问到树中的每一个结点:
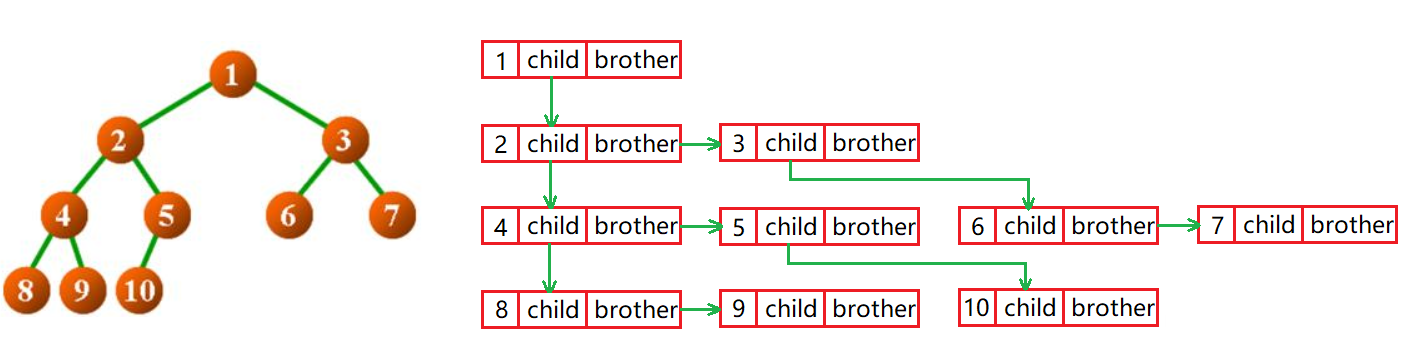
树在实际中的运用(表示文件系统的目录树结构)
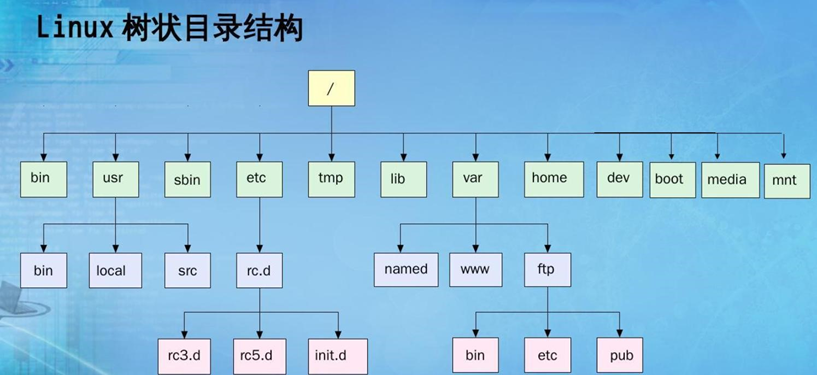
2.二叉树的概念及结构
二叉树概念
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵称为左子树和右子树的二叉树组成
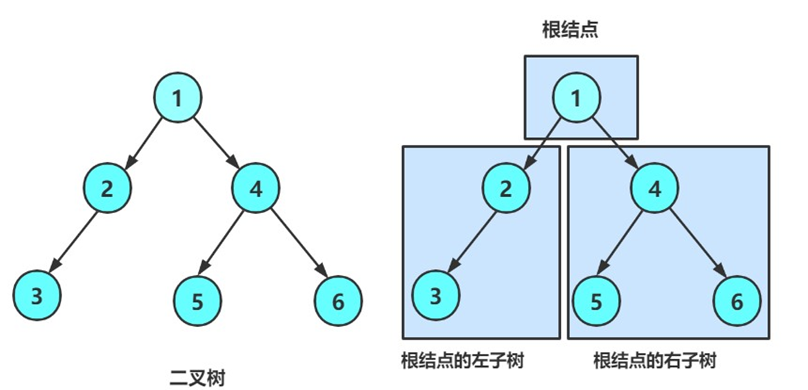
从上图可以看出:
- 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:
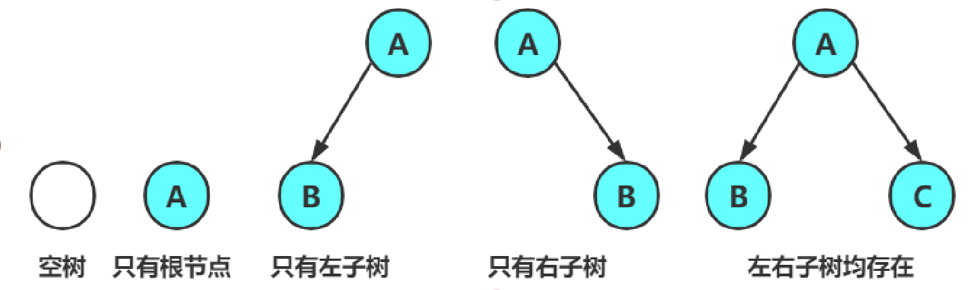
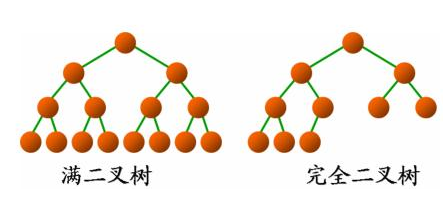
满二叉树和完全二叉树
- 满二叉树:一个二叉树,如果每一层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为k,且结点总数是2的k次方-1,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K,有N个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至N的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。
二叉树的性质
性质一:若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有2的(i-1)次方个结点。
性质二:若规定根结点的层数为1,则深度为h的二叉树的最大结点数为2的h次方-1个结点。
性质三:对任何一棵二叉树,如果度为0的叶结点个数为n0,度为2的分支结点个数为n2,则有n0 = n2+1。
性质四:若规定根结点的层数为1,则具有N个结点的满二叉树的深度h = log2(N+1)。
性质五:对于具有N个结点的完全二叉树,如果按照从上至下、从左至右的数组顺序对所有结点从0开始编号,
则对于序号为i的结点:
若 i > 0,则该结点的父结点序号为:( i - 1) / 2;若 i = 0,则无父结点。
若2i + 1 < N,则该结点的左孩子序号为:2i + 1;若2i + 1 >= N,则无左孩子。
若2i + 2 < N,则该结点的右孩子序号为:2i + 2;若2i + 2 >= N,则无右孩子。

二叉树的存储结构
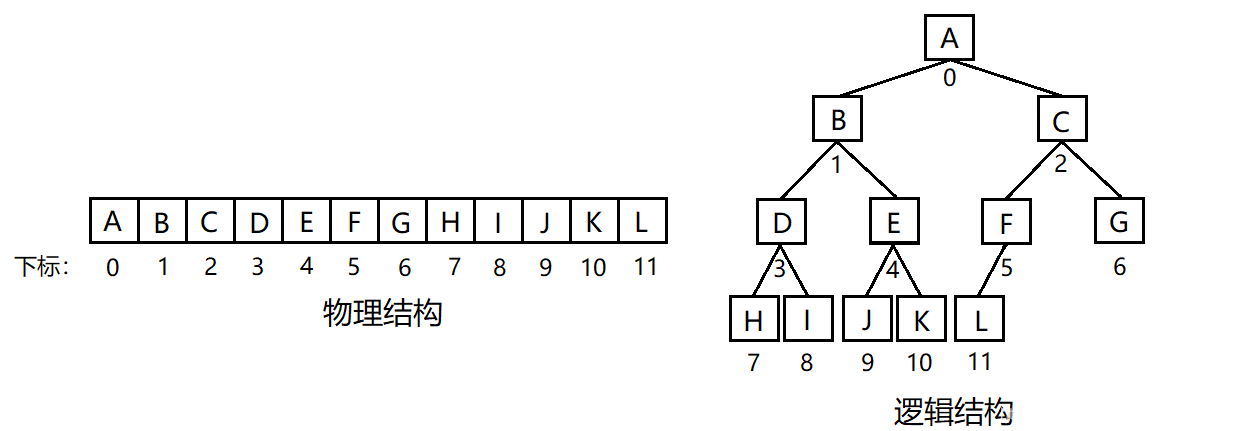
顺序结构
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实生活中只有堆(一种二叉树)才会使用数组来存储。二叉树的顺序存储在物理上是一个数组,在逻辑上是一棵二叉树。
链式结构
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素之间的逻辑关系。通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来存储该结点左孩子和右孩子所在的结点的地址。
链式结构又分为二叉链和三叉链,之后我们会用二叉链来实现二叉树的链式存储结构,三叉链运用于更高阶的数据结构,例如红黑树。

相关文章:

【数据结构】树和二叉树概念
1.树概念及结构 树概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。 有一个特殊的结点,…...
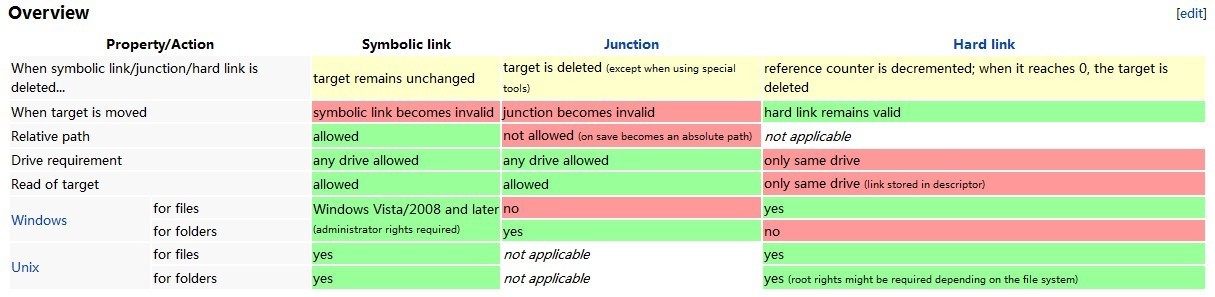
C盘清理教程
C盘清理教程 首先使用space Sniffer 扫一下c盘,然后看一下到底是哪个文件这么大 第二步,创建软链接。 首先将我们需要移动的文件的当前路径拷贝下来:C:\Users\Tom\Desktop\test-link\abc\ghi.txt 然后假设剪切到D盘下:D:\ghi.…...

【实战-05】 flinksql look up join
摘要 look up join 能做什么? 不饶关子直接说答案, look up join 就是 广播。 重要是事情说三遍,广播。flinksql中的look up join 就类似于flinks flink Datastream api中的广播的概念,但是又不完全相同,对于初次访问…...

C++数据结构--红黑树
目录 一、红黑树的概念二、红黑树的性质三、红黑树的节点的定义四、红黑树结构五、红黑树的插入操作参考代码 五、代码汇总 一、红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过…...

Linux perf使用思考
目录 一、参考资料(建议阅读)二、值得思考的几个问题1、perf使用不同的性能事件进行统计有什么区别呢?2、那使用不同的性能事件统计出来的数据?排序是如何决定的,其中的百分比数值在不同的性能事件进行统计时各自的意义…...

自定义路由断言工厂
我们来设定一个场景: 假设我们的应用仅仅让age在(min,max)之间的人来访问。 第1步:在配置文件中,添加一个Age的断言配置 spring: application:name: api-gateway cloud:nacos:discovery:server-addr: 127.0.0.1:8848gateway:discovery:locator:enabled: trueroute…...
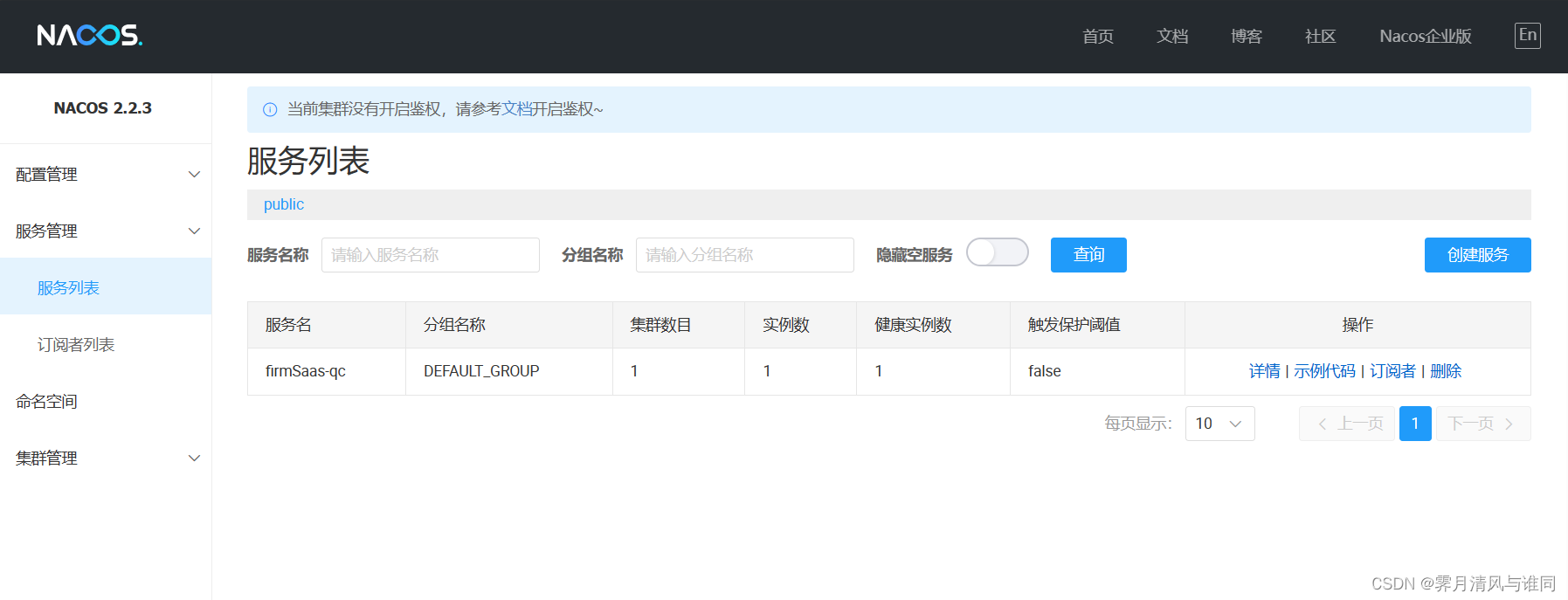
Nacos安装及在项目中的使用
目录 概要一、安装 Nacos1、下载 Nacos2、解压3、启动 Nacos 服务器4、自定义Nacos启动脚本5、访问Nacos Web控制台 二、Nacos----服务注册与发现1、添加 Nacos 依赖2、配置 Nacos 服务器地址3、使用 Nacos 注册服务4、启动服务 三、Nacos----配置管理1、创建配置数据2、从 Nac…...

overleaf中latex语法总结
α和bata $\alpha$ $\beta$上标和下标同时使用 $A_{IJ}^{IJ}$\\ %上标^下标_多个使用{}行内公式 \noindent $abc$\\ %行内公式\documentclass{article} \usepackage[utf8]{inputenc} \usepackage[namelimits]{amsmath} %数学公式 \usepackage{amssymb} %数学公式…...
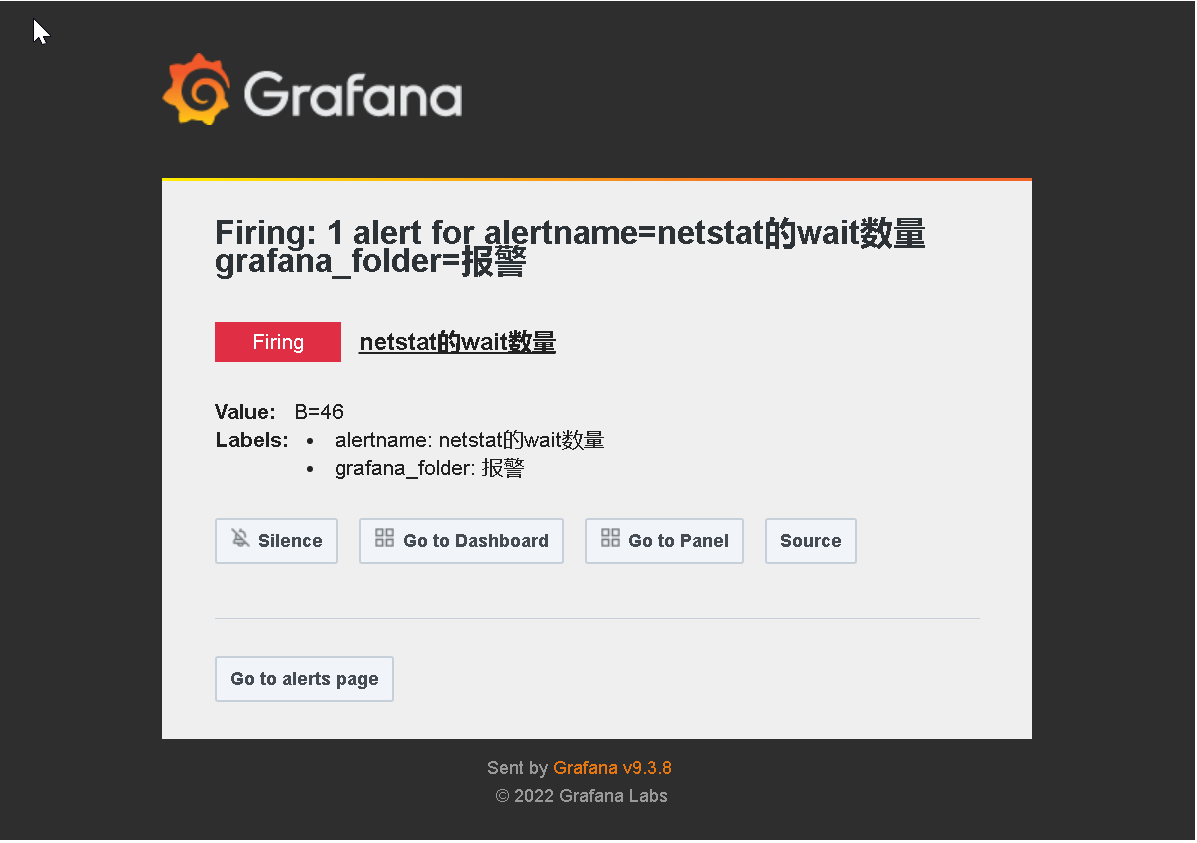
Grafana配置邮件告警
1、创建一个监控图 2、grafana邮件配置 vim /etc/grafana/grafana.ini [smtp] enabled true host smtp.163.com:465 user qinziteng05163.com password xxxxx # 授权码 from_address qinziteng05163.com from_name Grafanasystemctl restart grafana-serv…...

setup中的nextTick函数
await nextTick() 是 Vue 3 的一个异步函数,用于等待 DOM 更新完成后执行回调函数, 它在 setup 函数中非常有用,可以确保在对 DOM 进行操作之前,先等待 Vue 完成相关的 DOM 更新。 下面是一个示例,演示了 await nextT…...
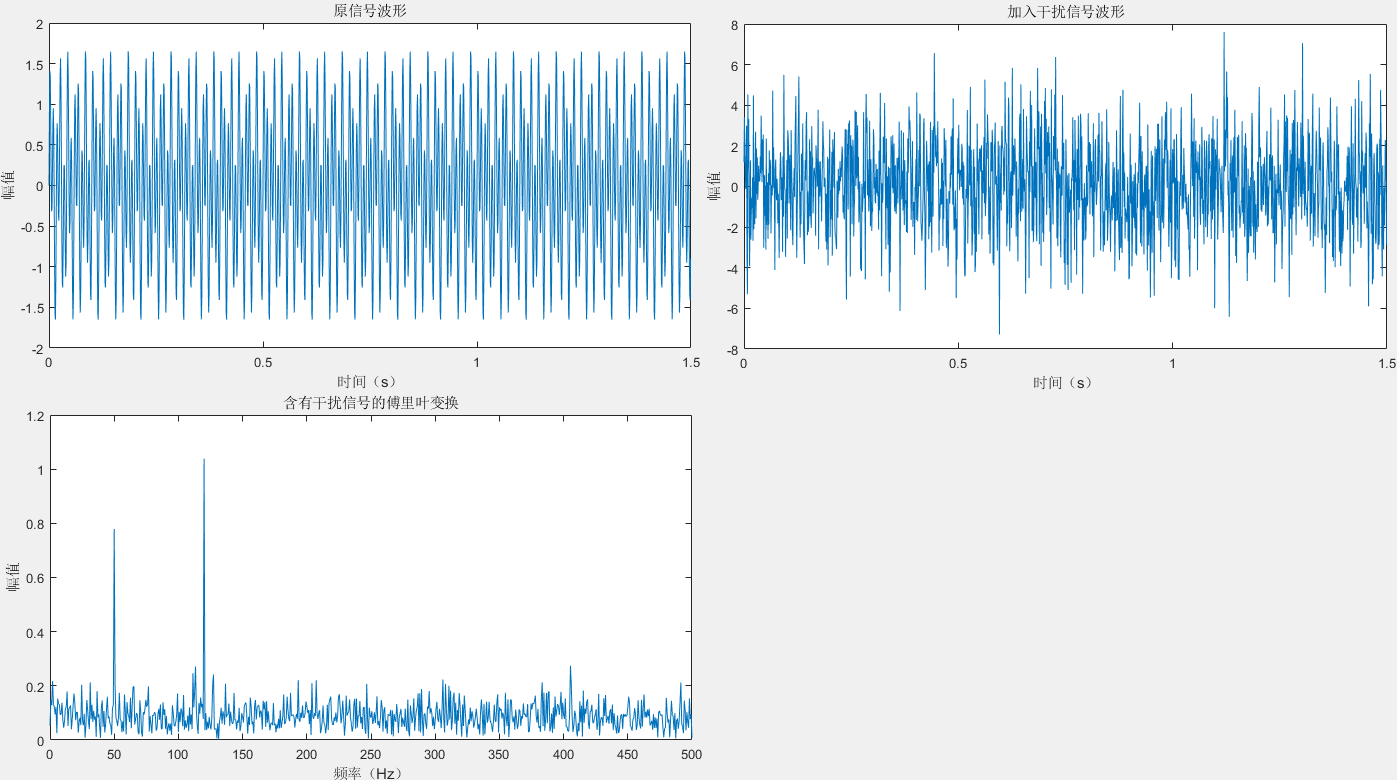
Matlab信号处理3:fft(快速傅里叶变换)标准使用方式
Fs 1000; % 采样频率 T 1/Fs; % 采样周期:0.001s L 1500; % 信号长度 t (0:L-1)*T; % 时间向量. 时间向量从0开始递增,0s~1.499sS 0.7*sin(2*pi*50*t) sin(2*pi*120*t); % 模拟原信号 X S 2*randn(size(t)); …...

Python|合并两个字典的几种方法
在Python中,有多种方法可以通过使用各种函数和构造函数来合并字典。在本文中,我们将讨论一些合并字典的方法。 1. 使用方法update() 通过使用Python中的update()方法,可以将一个列表合并到另一个列表中。但是在这种情况下,第二个…...

ElementUI浅尝辄止24:Message 消息提示
常用于主动操作后的反馈提示。与 Notification 的区别是后者更多用于系统级通知的被动提醒。 1.如何使用? Message 在配置上与 Notification 非常类似,所以部分 options 在此不做详尽解释,可以结合 Notification 的文档理解它们。Element 注…...

让照片动起来的软件,轻松制作照片动效
随着社交媒体的日益普及,我们对于照片的要求也越来越高。普通的照片已经不能满足我们的需求,我们希望照片更加生动有趣。照片动效便应运而生,它可以让照片动起来,吸引更多的注意力,让照片更加生动有趣。 照片动效制作起…...

【图解RabbitMQ-7】图解RabbitMQ五种队列模型(简单模型、工作模型、发布订阅模型、路由模型、主题模型)及代码实现
🧑💻作者名称:DaenCode 🎤作者简介:CSDN实力新星,后端开发两年经验,曾担任甲方技术代表,业余独自创办智源恩创网络科技工作室。会点点Java相关技术栈、帆软报表、低代码平台快速开…...

Linux命令200例:write用于向特定用户或特定终端发送信息
🏆作者简介,黑夜开发者,CSDN领军人物,全栈领域优质创作者✌。CSDN专家博主,阿里云社区专家博主,2023年6月csdn上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师࿰…...
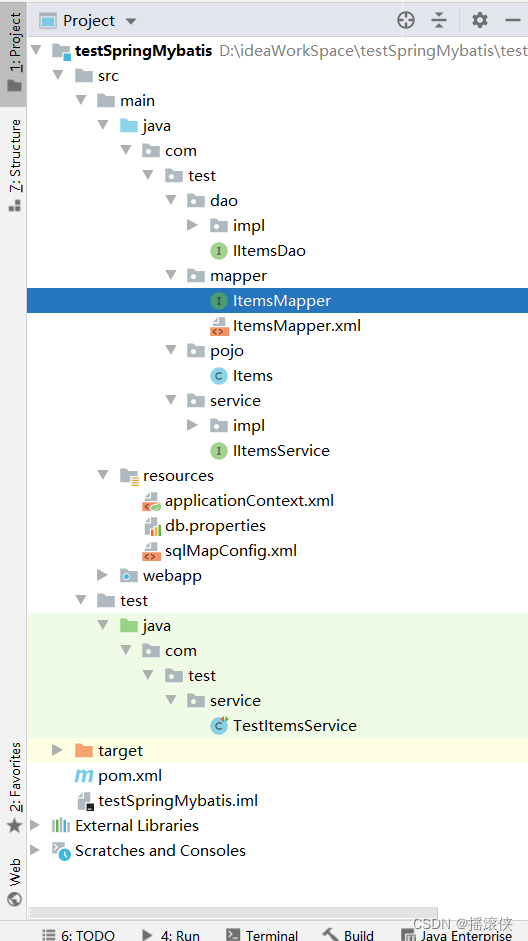
javaee spring整合mybatis spring帮我们创建dao层
项目结构 pom依赖 <?xml version"1.0" encoding"UTF-8"?><project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/P…...
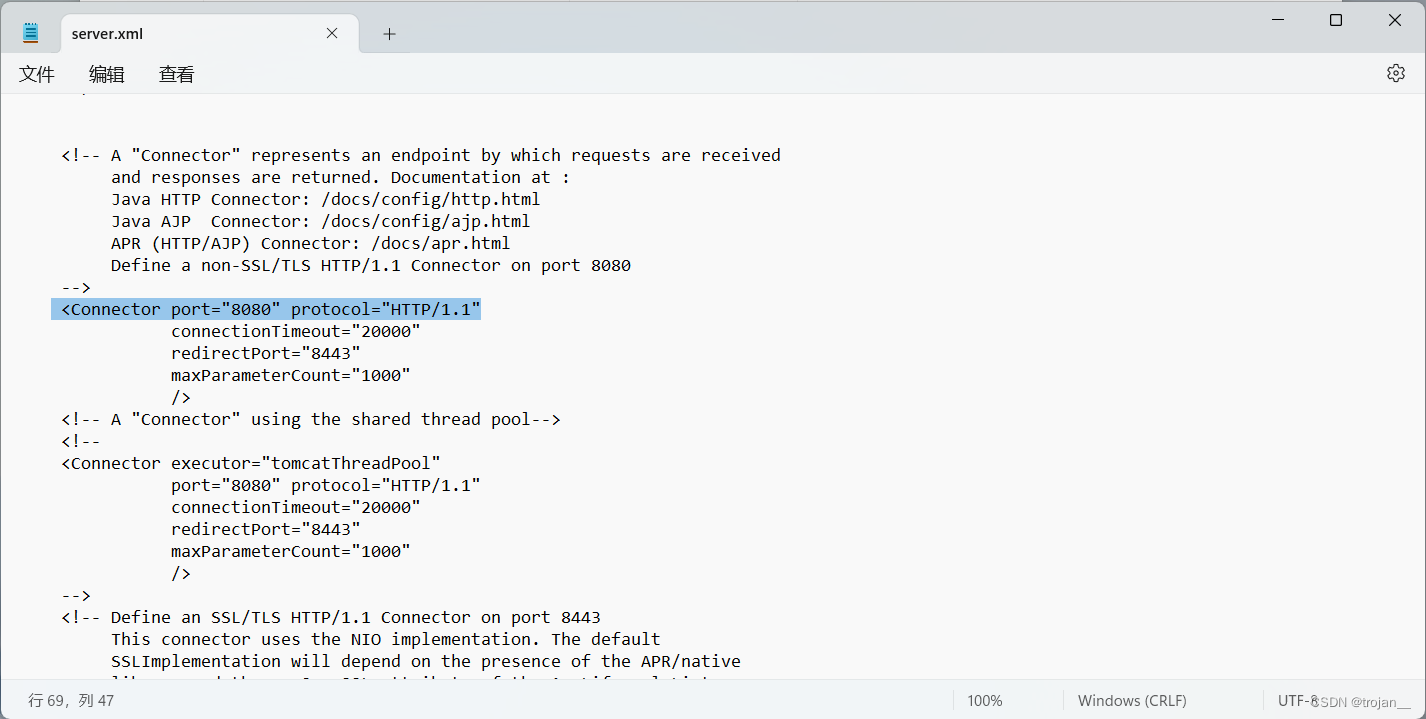
修改Tomcat的默认端口号
1、找到Tomcat的安装路径。 2、打开conf文件夹。 3、用记事本打开server.xml文件 4、找到 <Connector port"8080" protocol"HTTP/1.1",其中的8080就是tomcat的默认端口,将其修改为你需要的端口即可。...

Open3D Ransac拟合空间直线(python详细过程版)
RANSAC拟合直线 一、算法原理1、算法简介2、参考文献二、代码实现三、结果展示本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫。 一、算法原理 1、算法简介 见:Open3D——RANSAC 三维点云空间直线拟合 2、参考文献...

题目:2729.判断一个数是否迷人
题目来源: leetcode题目,网址:2729. 判断一个数是否迷人 - 力扣(LeetCode) 解题思路: 对 n,2*n,3*n 中的数字出现次数计数,若数字 0 出现 0 次,数字 1~9…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
