当前位置： 首页 > news >正文

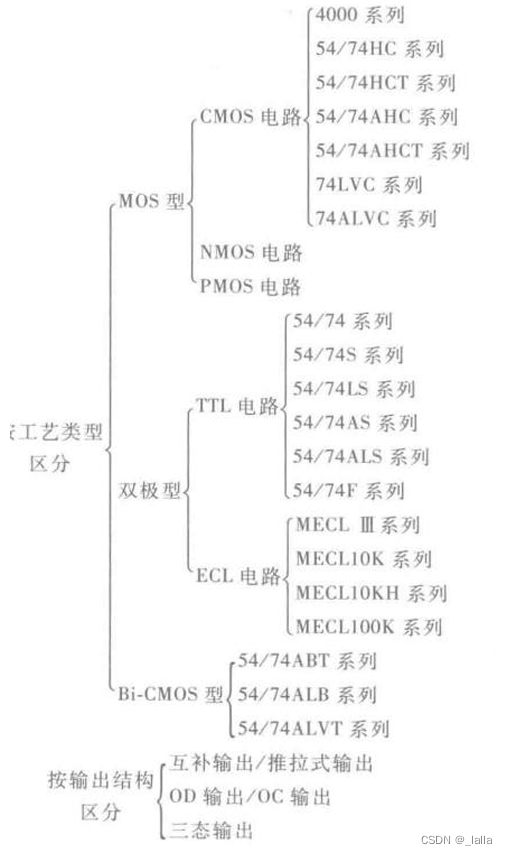
verilog学习笔记7——PMOS和NMOS、TTL电路和CMOS电路

news 2026/1/30 16:45:21

文章目录

  • 前言
  • 一、PMOS和NMOS
    • 1、NMOS
    • 2、PMOS
    • 3、增强型和耗尽型
    • 4、两者面积大小
  • 二、CMOS门电路
    • 1、非门
    • 2、与非门
    • 3、或非门
    • 4、线与逻辑
    • 5、CMOS传输门
    • 6、三态门
  • 三、TTL电路
  • 四、TTL电路 VS CMOS电路
  • 五、数字电平
  • 六、使用CMOS电路实现逻辑函数
    • 1、上拉网络 PUN
    • 2、下拉网络 PDN
    • 3、实现逻辑表达式

前言

2023.9.7

在这里插入图片描述

一、PMOS和NMOS

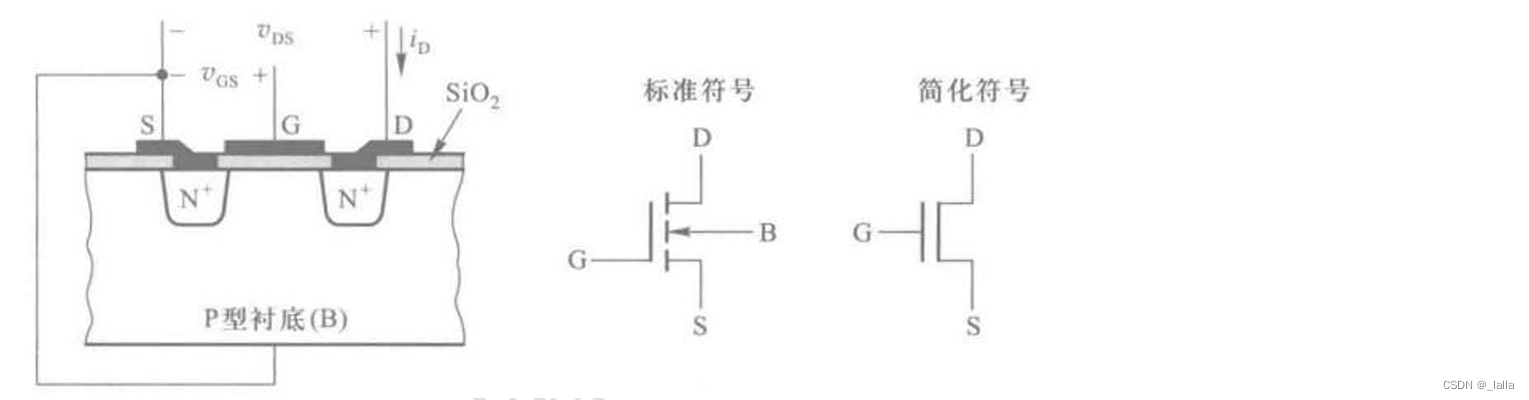
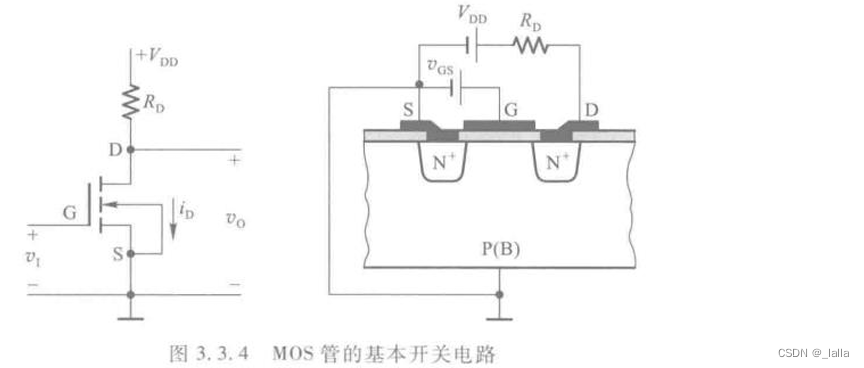
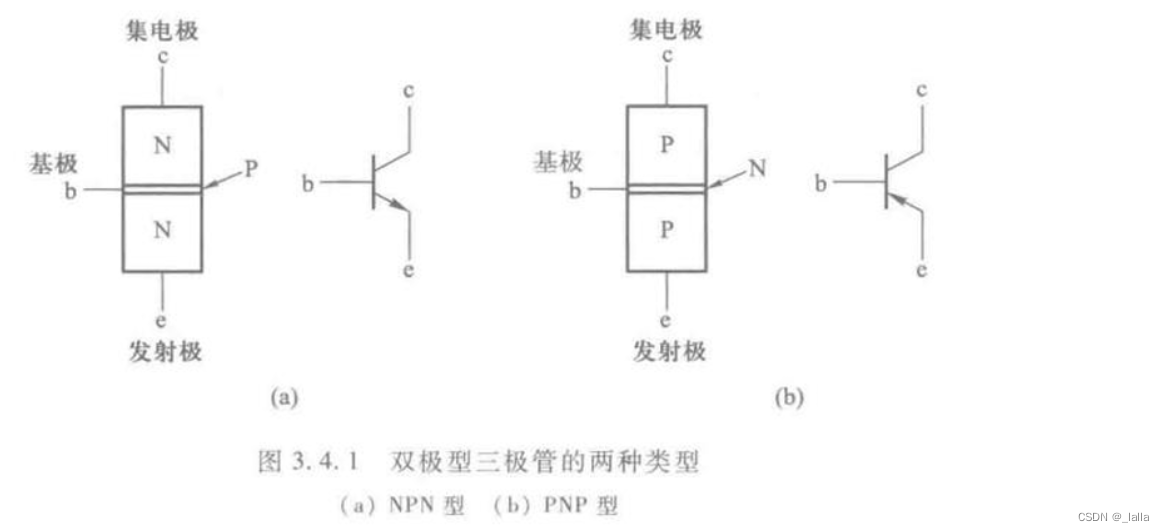
1、NMOS

截止区：VGS<VGS(th)
放大区、恒流区

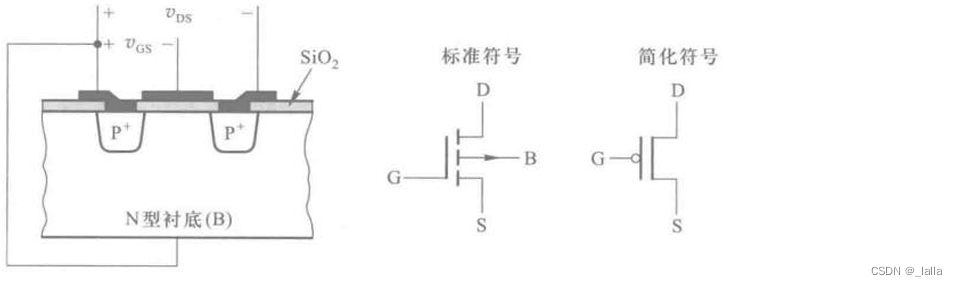
在这里插入图片描述

在这里插入图片描述

2、PMOS

缺点：使用的是负电压电源，不便于和TTL电路连接，使用的少

在这里插入图片描述

3、增强型和耗尽型

耗尽型：在栅极下面的二氧化硅绝缘层里面掺杂了正离子（NMOS），使得正常情况下导电沟道已经存在，需要施加负电压使得导电沟道消失

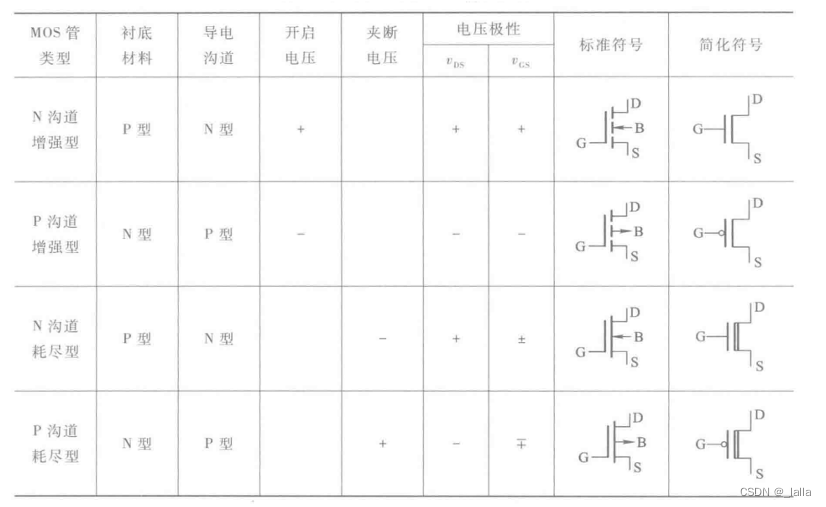
在这里插入图片描述

4、两者面积大小

如果把MOS管的面积增加，那么流过mos管的电流更大，速度也更快，驱动电路更强

笔试题1：PMOS和NMOS哪个面积更大

二、CMOS门电路

1、非门

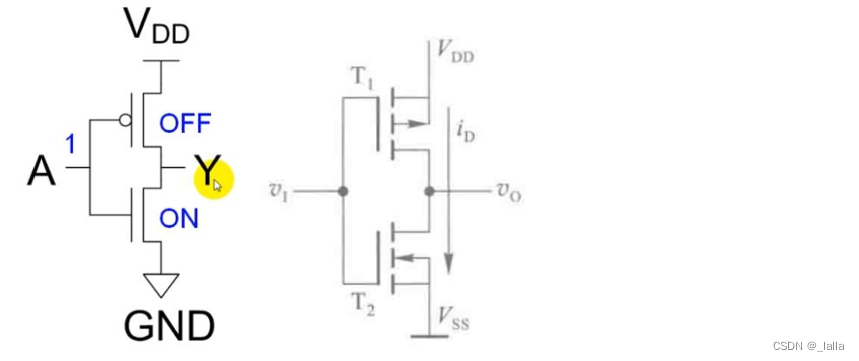
在这里插入图片描述

2、与非门

n输入的与非门：n个pmos并联 + n个nmos串联

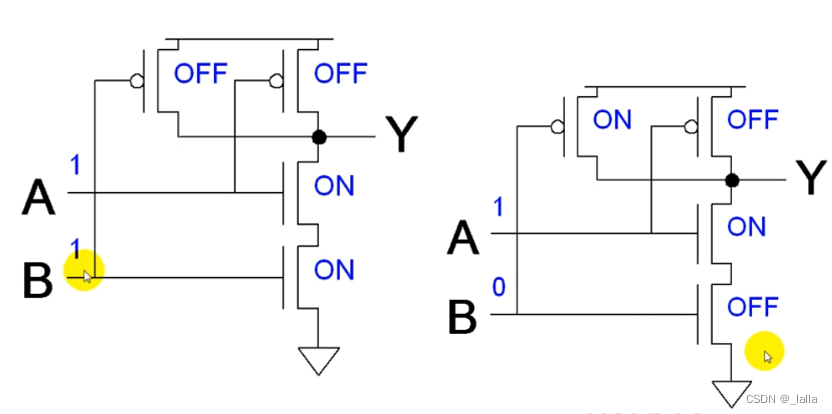
在这里插入图片描述
在这里插入图片描述

3、或非门

n输入或非门：n个pmos串联 + n个nmos并联
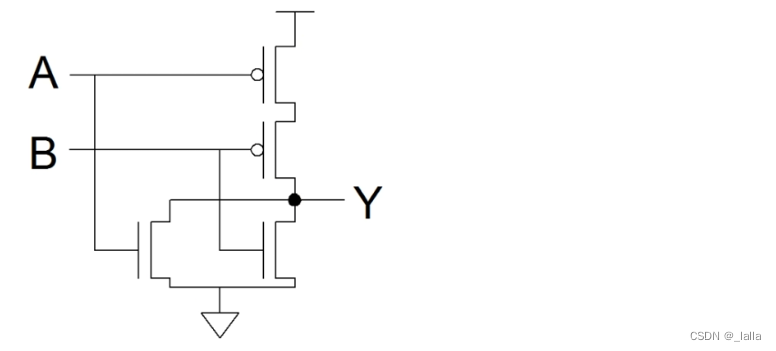
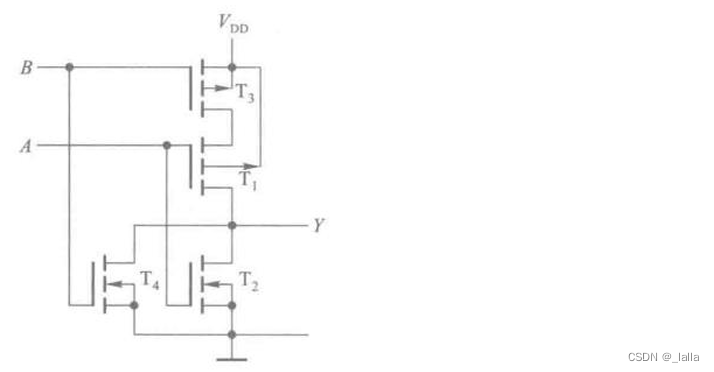
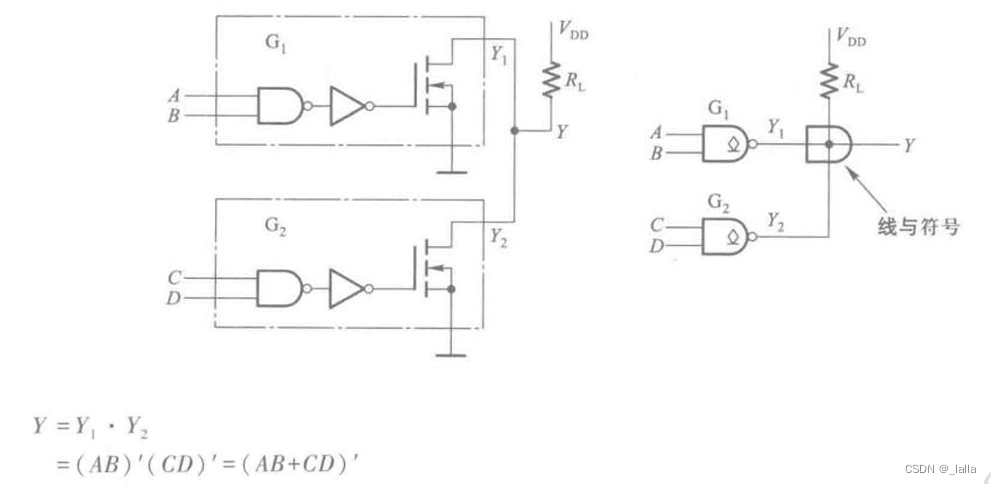
在这里插入图片描述
在这里插入图片描述

4、线与逻辑

线与：多个信号相连实现与的功能
上拉电阻：防止电流过大
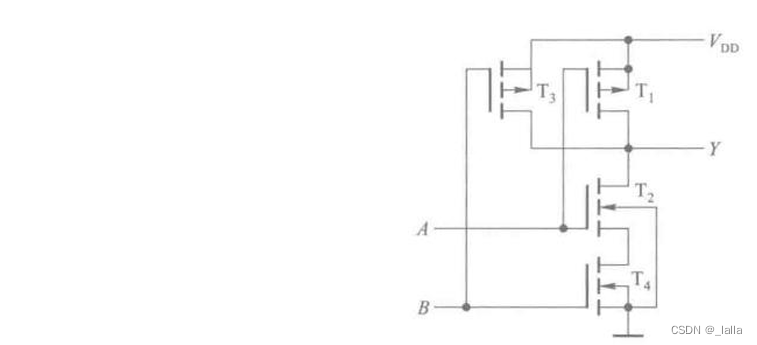
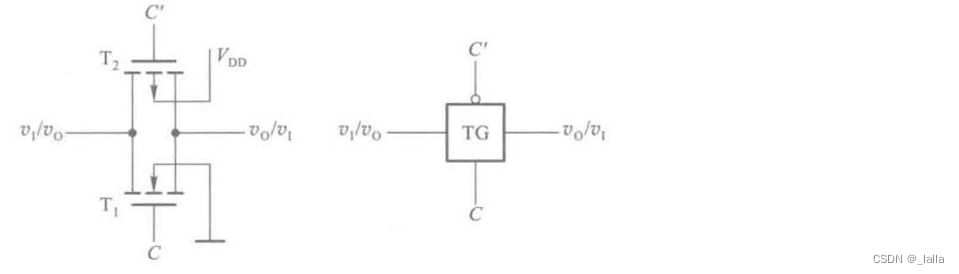
在这里插入图片描述

5、CMOS传输门

只用一个mos管：会存在压降
在这里插入图片描述

在这里插入图片描述

用非门和CMOS传输门实现异或电路
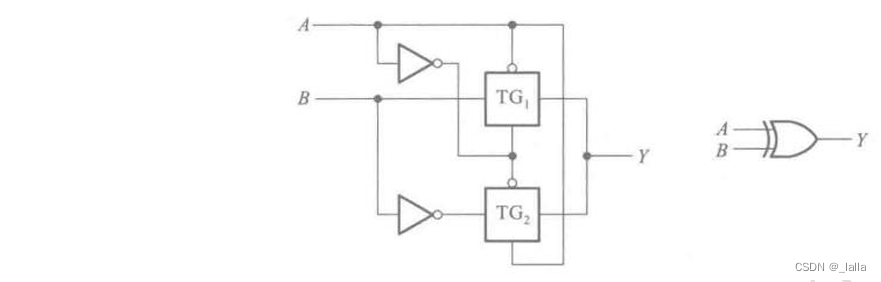
在这里插入图片描述

6、三态门

三态门：既不是0，也不是1，电阻很大，相当于开路

在这里插入图片描述

always@(din or en)beginif(en)dout = din;elsedout = 1'bz;
end//或者assign赋值
assign dout = en ? din : 1'bz;

三、TTL电路

CMOS输出接口可以直接连TTL电路
TTL电路需要加上拉电阻接到CMOS端口

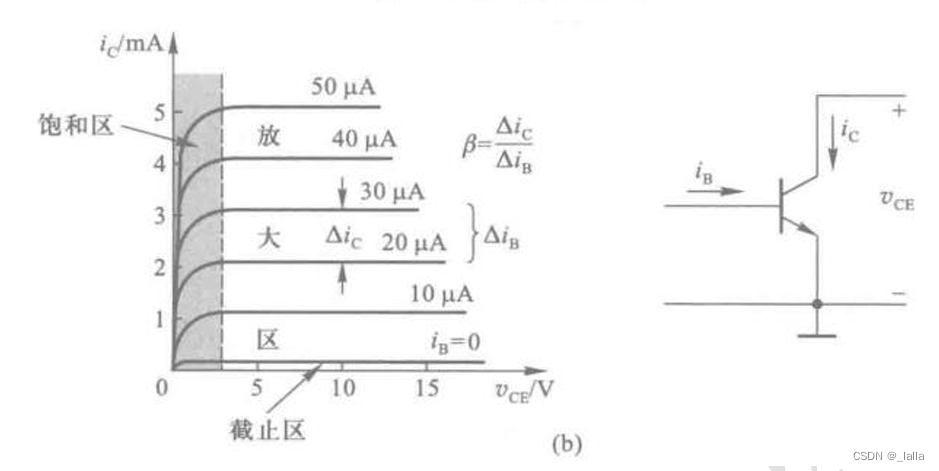
在这里插入图片描述
放大区：ic随着iB正比增加，系数为放大因子
饱和区：ic不再随着ib比例增加，逐渐趋于饱和
截止区：ic几乎为零
在这里插入图片描述

四、TTL电路 VS CMOS电路

CMOSTTL
电压控器件电流控器件
功耗低功耗高
速度慢速度快
12V、5V0.3~3.6V

五、数字电平

Voh：保证输出为高电平的最小输出电压
Vih：保证输入为高电平的最小输入电压
Vil：保证输入为低电平的最大输入电压
Vol：保证输出为高电平的最小输出电压

大小关系：Voh > Vih > Vth > Vil > Vol

六、使用CMOS电路实现逻辑函数

参考链接：CMOS逻辑门电路

组成：NMOS下拉晶体管 + PMOS上拉晶体管组成
两个网络在变量的控制下做出相反的行为

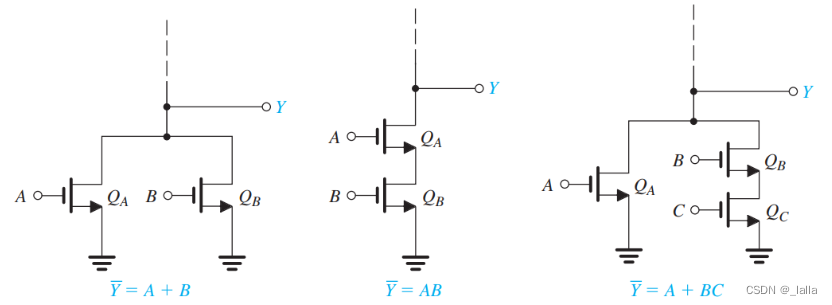
1、上拉网络 PUN

可以等效为

Y = ~(A + B);
Y = ~(AB);
Y = ~(A + BC);

在这里插入图片描述

2、下拉网络 PDN

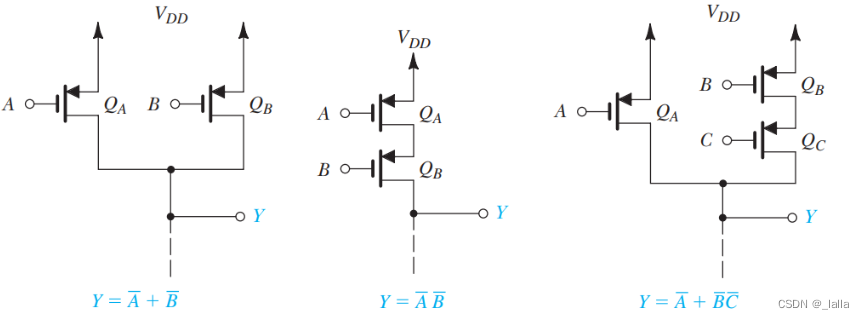
在这里插入图片描述

3、实现逻辑表达式

3.1 下面表达式是整体反相，因此可以用PDN来表示

在这里插入图片描述
PUN是变量反相
在这里插入图片描述

CMOS电路如下图所示：

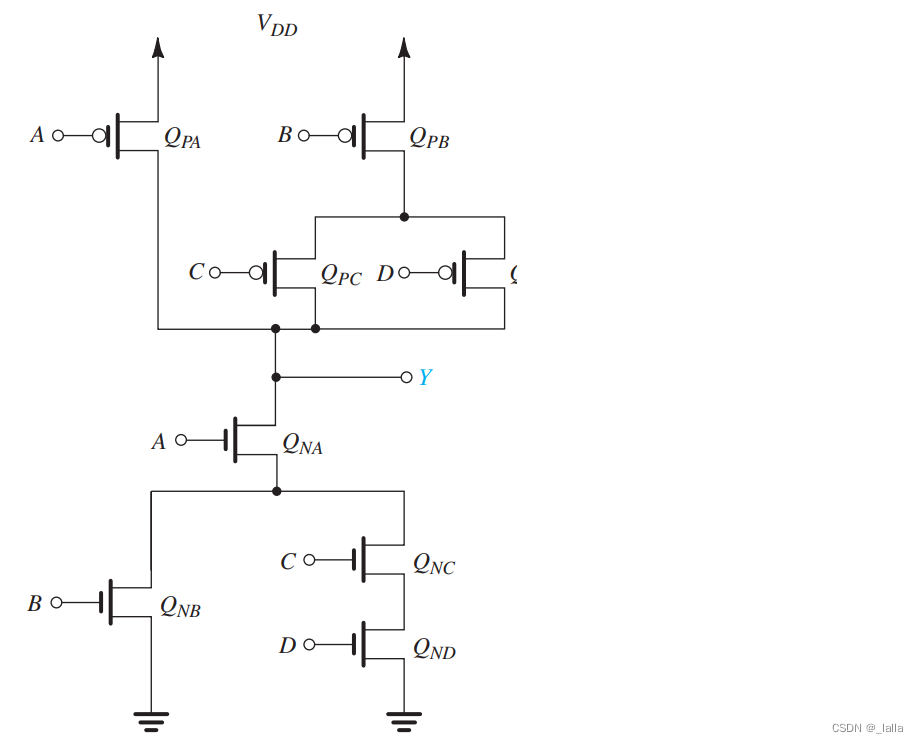
在这里插入图片描述

3.2 异或门实现

分析：异或门中间既不是整体取反，也不是每个都是反变量，而是有原变量和反变量夹杂在一起
在这里插入图片描述
在这里插入图片描述

CMOS电路如下图所示：
有两个变量的输入需要增加非门，因此总共需要12个mos管实现
注意：下面的电路实现不再是对偶网络，网络对偶并不是必要条件
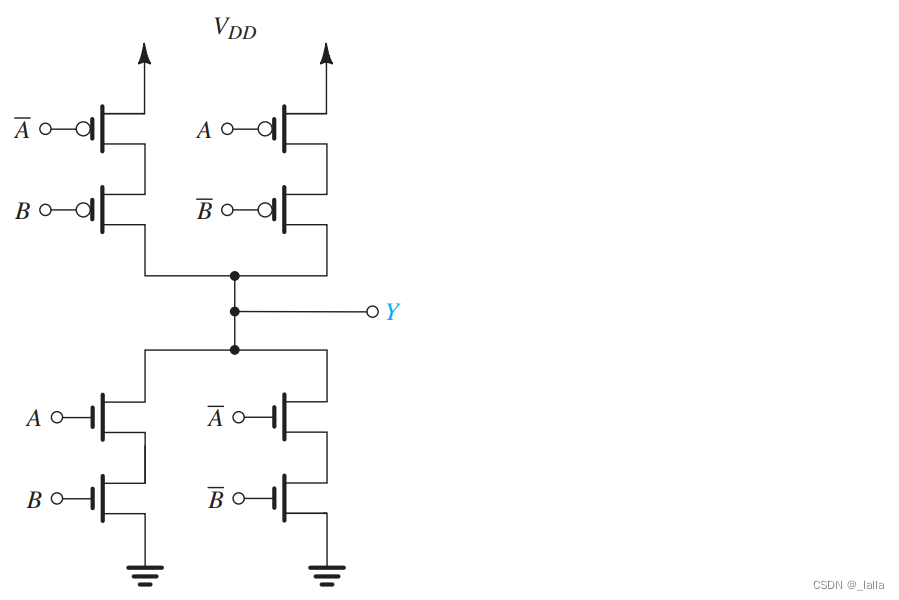
在这里插入图片描述

3.3 笔试题

Y = ~(D + A(B + C))     //这个和上面的3.1类似，属于整体反相的那种

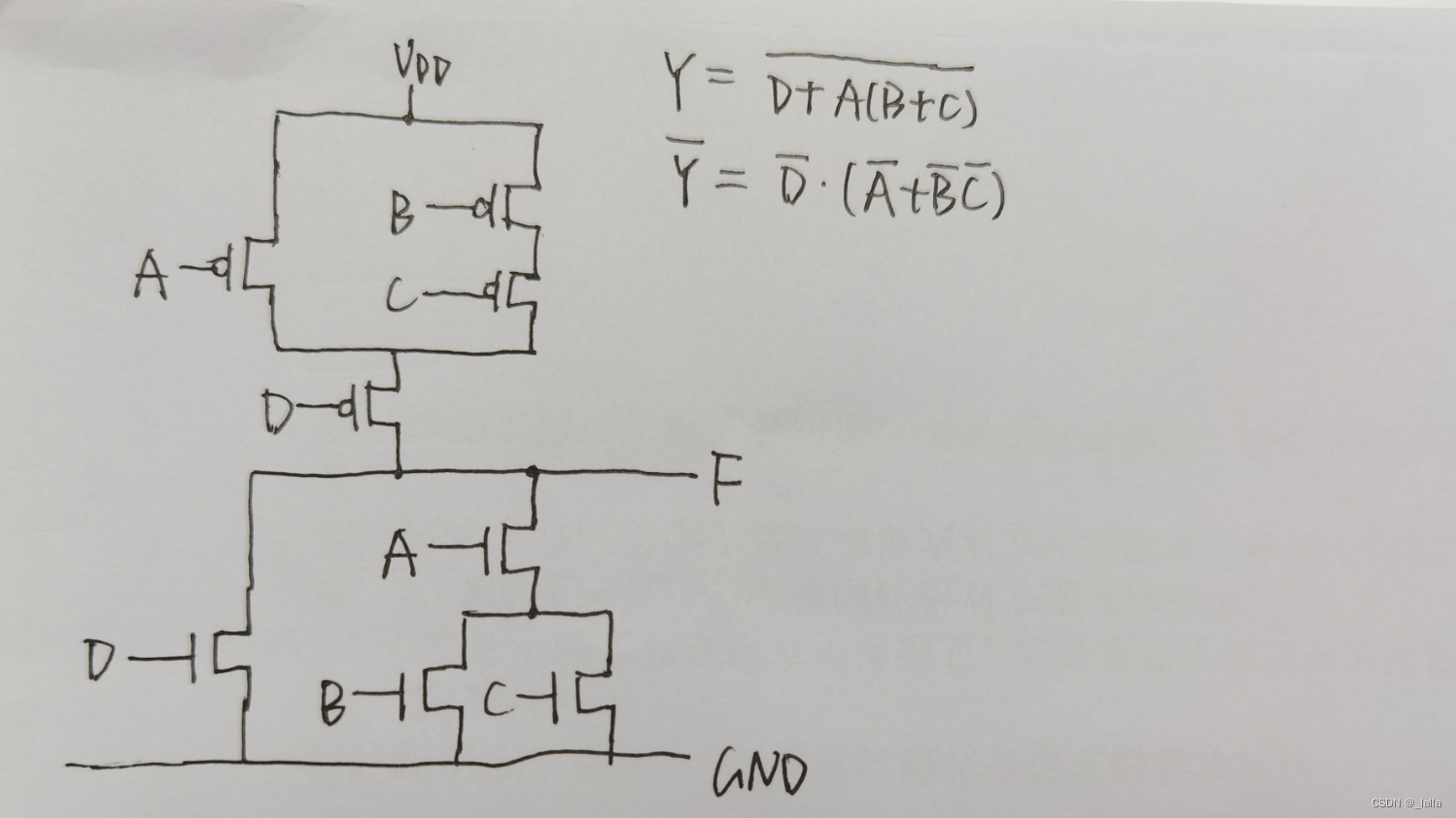
在这里插入图片描述

Y = AB + ~(CD)

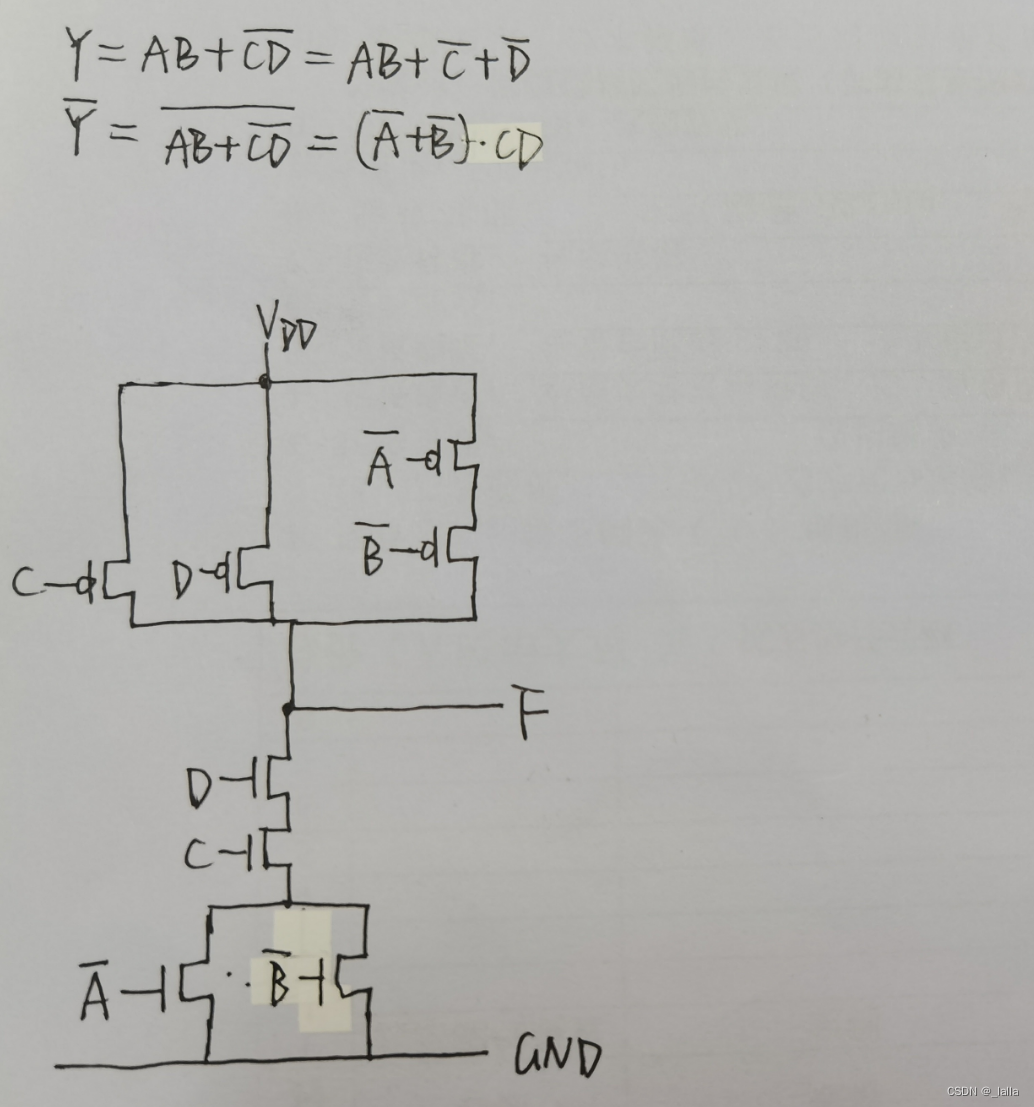
在这里插入图片描述

Y = AB + C

两种方式实现：
第一种当作整体取反，最后加个非门，这样实现门电路最少
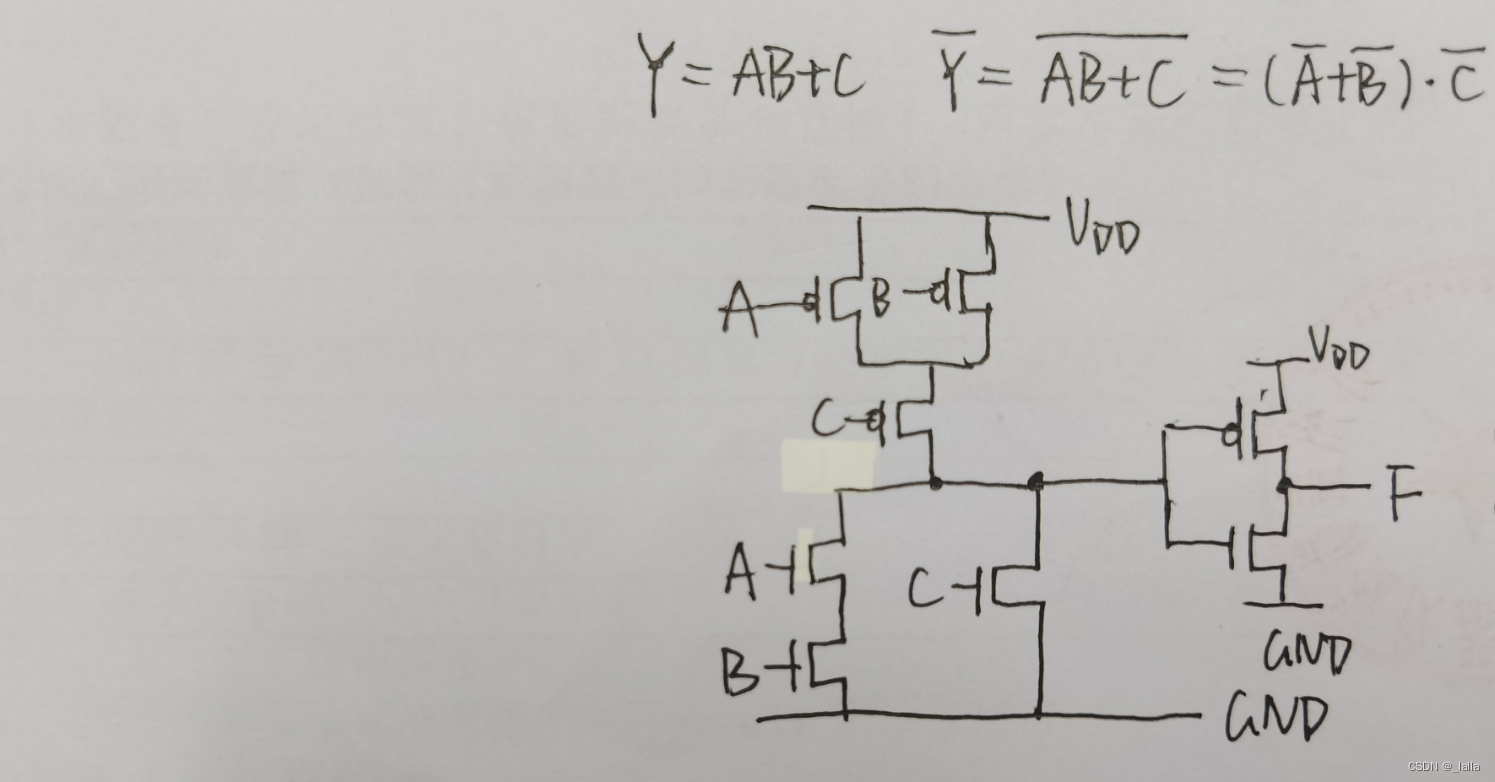
在这里插入图片描述

第二种 直接根据表达式分别写出上拉和下拉网络
在这里插入图片描述

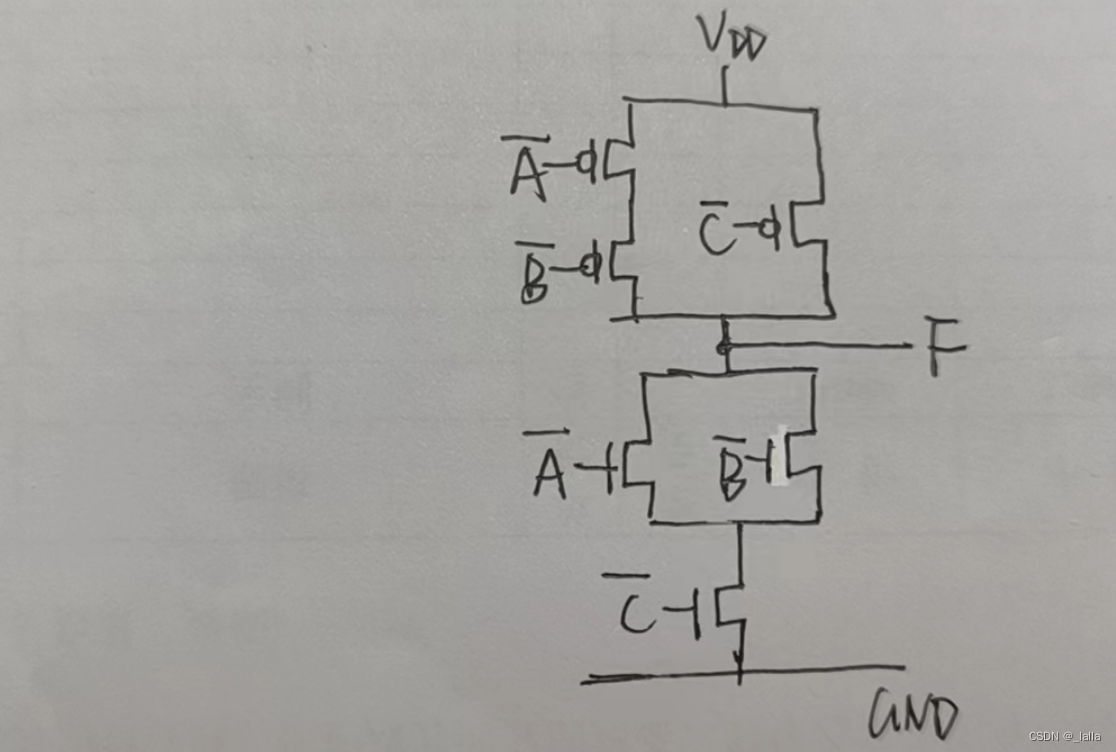
总结：除了同时包含原变量和反变量的时候，网络不是对称的，下面这几个都还是对偶网络

相关文章：

verilog学习笔记7——PMOS和NMOS、TTL电路和CMOS电路

文章目录 前言一、PMOS和NMOS1、NMOS2、PMOS3、增强型和耗尽型4、两者面积大小 二、CMOS门电路1、非门2、与非门3、或非门4、线与逻辑5、CMOS传输门6、三态门 三、TTL电路四、TTL电路 VS CMOS电路五、数字电平六、使用CMOS电路实现逻辑函数1、上拉网络 PUN2、下拉网络 PDN3、实…...

编程日记 2023/9/12 10:09:04

Java知识点二

Java知识点二 1、Comparable内部比较器&#xff0c;Comparator外部比较器2、源码结构的区别:1&#xff09;Comparable接口&#xff1a;2&#xff09;Comparator接口&#xff1a; 2、Java反射 1、Comparable内部比较器&#xff0c;Comparator外部比较器 我们一般把Comparable叫…...

编程日记 2023/9/12 10:08:02

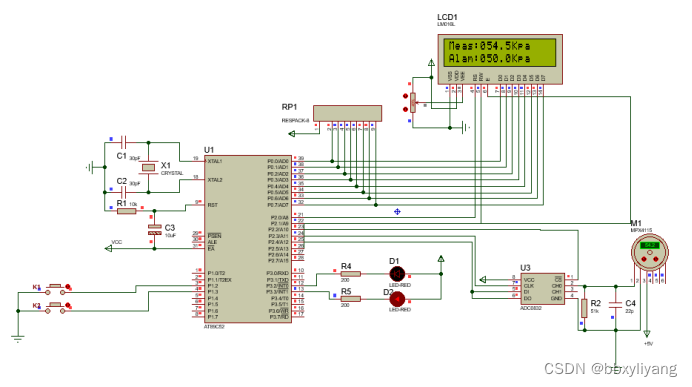
基于单片机压力传感器MPX4115检测-报警系统-proteus仿真-源程序

一、系统方案 本设计采用52单片机作为主控器&#xff0c;液晶1602显示&#xff0c;MPX4115检测压力&#xff0c;按键设置报警&#xff0c;LED报警。 二、硬件设计 原理图如下&#xff1a; 三、单片机软件设计 1、首先是系统初始化 /***************************************…...

编程日记 2023/9/12 10:07:00

Pytorch02 神经网路搭建步骤

文章目录 import numpy as np import torch from PIL.Image import Image from torch.autograd import Variable# 获取数据 def get_data():train_Xnp.asarray([3.3,4.4,5.5,6.71,6.93,4.168,9.779,6.182,7.59,2.167,7.042,10.791,5.313,7.997,5.654,9.27,3.1])train_Ynp.asarr…...

编程日记 2023/9/12 10:05:58

【源码】JavaWeb+Mysql招聘管理系统 课设

简介 用idea和eclipse都可以&#xff0c;数据库是mysql&#xff0c;这是一个Java和mysql做的web系统&#xff0c;用于期末课设作业 cout<<"如果需要的小伙伴可以http://www.codeying.top";可定做课设 线上招聘平台整合了各种就业指导资源&#xff0c;通过了…...

编程日记 2023/9/12 10:04:57

Java中级编程大师班＜第一篇：初识数据结构与算法-数组(2)＞

数组&#xff08;Array&#xff09; 数组是计算机编程中最基本的数据结构之一。它是一个有序的元素集合&#xff0c;每个元素都可以通过索引进行访问。本文将详细介绍数组的特性、用法和注意事项。 数组的基本特性 数组具有以下基本特性&#xff1a; 有序性&#xff1a; 数…...

编程日记 2023/9/12 10:03:56

杰哥教你面试之一百问系列:java集合

文章目录 1. 什么是Java集合&#xff1f;请简要介绍一下集合框架。2. Java集合框架主要分为哪几种类型&#xff1f;3. 什么是迭代器&#xff08;Iterator&#xff09;&#xff1f;它的作用是什么&#xff1f;4. ArrayList和LinkedList有什么区别&#xff1f;它们何时适用&#…...

编程日记 2023/9/12 10:02:55

【数据结构】树和二叉树概念

1.树概念及结构 树概念 树是一种非线性的数据结构&#xff0c;它是由n&#xff08;n>0&#xff09;个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树&#xff0c;也就是说它是根朝上&#xff0c;而叶朝下的。 有一个特殊的结点&#xff0c;…...

编程日记 2023/9/12 10:01:54

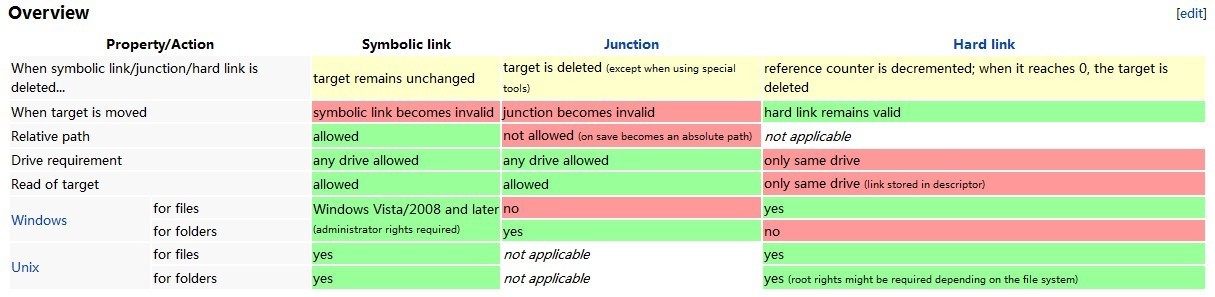
C盘清理教程

C盘清理教程 首先使用space Sniffer 扫一下c盘&#xff0c;然后看一下到底是哪个文件这么大 第二步&#xff0c;创建软链接。 首先将我们需要移动的文件的当前路径拷贝下来&#xff1a;C:\Users\Tom\Desktop\test-link\abc\ghi.txt 然后假设剪切到D盘下&#xff1a;D:\ghi.…...

编程日记 2023/9/12 10:00:53

【实战-05】 flinksql look up join

摘要 look up join 能做什么&#xff1f; 不饶关子直接说答案&#xff0c; look up join 就是 广播。 重要是事情说三遍&#xff0c;广播。flinksql中的look up join 就类似于flinks flink Datastream api中的广播的概念&#xff0c;但是又不完全相同&#xff0c;对于初次访问…...

编程日记 2023/9/12 9:59:52

C++数据结构--红黑树

目录 一、红黑树的概念二、红黑树的性质三、红黑树的节点的定义四、红黑树结构五、红黑树的插入操作参考代码 五、代码汇总 一、红黑树的概念 红黑树&#xff0c;是一种二叉搜索树&#xff0c;但在每个结点上增加一个存储位表示结点的颜色&#xff0c;可以是Red或Black。 通过…...

编程日记 2023/9/12 9:58:50

Linux perf使用思考

目录 一、参考资料&#xff08;建议阅读&#xff09;二、值得思考的几个问题1、perf使用不同的性能事件进行统计有什么区别呢&#xff1f;2、那使用不同的性能事件统计出来的数据&#xff1f;排序是如何决定的&#xff0c;其中的百分比数值在不同的性能事件进行统计时各自的意义…...

编程日记 2023/9/12 9:57:49

自定义路由断言工厂

我们来设定一个场景: 假设我们的应用仅仅让age在(min,max)之间的人来访问。 第1步&#xff1a;在配置文件中,添加一个Age的断言配置 spring: application:name: api-gateway cloud:nacos:discovery:server-addr: 127.0.0.1:8848gateway:discovery:locator:enabled: trueroute…...

编程日记 2023/9/12 9:56:48

Nacos安装及在项目中的使用

目录 概要一、安装 Nacos1、下载 Nacos2、解压3、启动 Nacos 服务器4、自定义Nacos启动脚本5、访问Nacos Web控制台 二、Nacos----服务注册与发现1、添加 Nacos 依赖2、配置 Nacos 服务器地址3、使用 Nacos 注册服务4、启动服务 三、Nacos----配置管理1、创建配置数据2、从 Nac…...

编程日记 2023/9/12 9:55:48

overleaf中latex语法总结

α和bata $\alpha$ $\beta$上标和下标同时使用 $A_{IJ}^{IJ}$\\ %上标^下标_多个使用{}行内公式 \noindent $abc$\\ %行内公式\documentclass{article} \usepackage[utf8]{inputenc} \usepackage[namelimits]{amsmath} %数学公式 \usepackage{amssymb} %数学公式…...

编程日记 2023/9/12 9:54:47

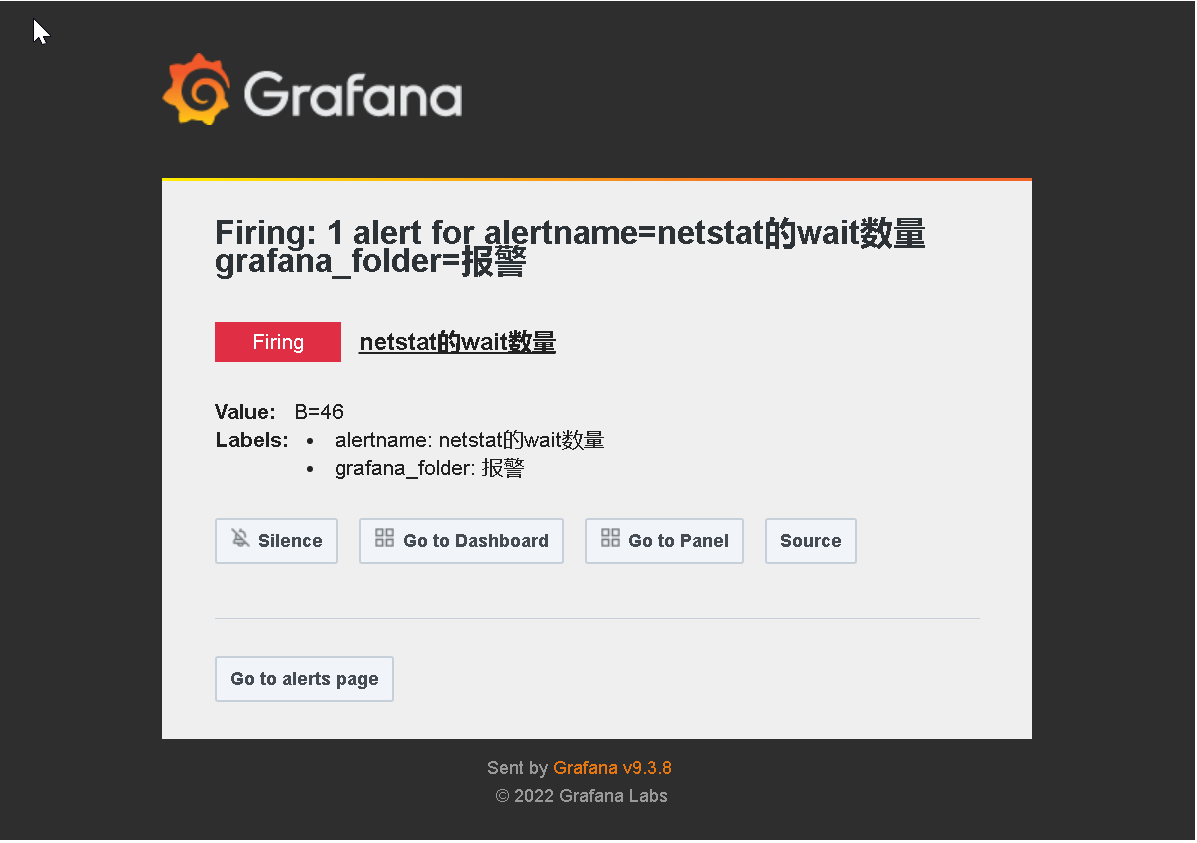
Grafana配置邮件告警

1、创建一个监控图 2、grafana邮件配置 vim /etc/grafana/grafana.ini [smtp] enabled true host smtp.163.com:465 user qinziteng05163.com password xxxxx # 授权码 from_address qinziteng05163.com from_name Grafanasystemctl restart grafana-serv…...

编程日记 2023/9/12 9:53:46

setup中的nextTick函数

await nextTick() 是 Vue 3 的一个异步函数&#xff0c;用于等待 DOM 更新完成后执行回调函数&#xff0c; 它在 setup 函数中非常有用&#xff0c;可以确保在对 DOM 进行操作之前&#xff0c;先等待 Vue 完成相关的 DOM 更新。 下面是一个示例&#xff0c;演示了 await nextT…...

编程日记 2023/9/12 9:52:44

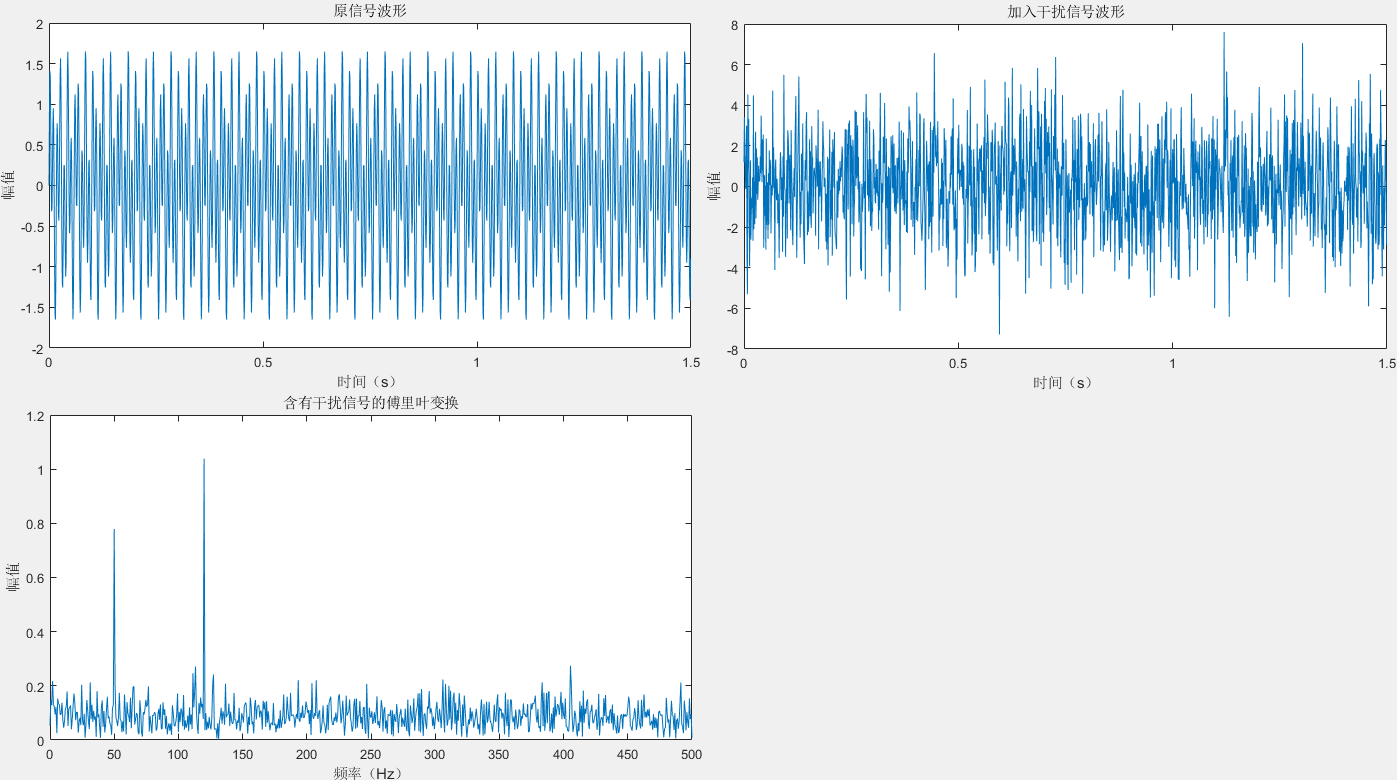
Matlab信号处理3：fft(快速傅里叶变换)标准使用方式

Fs 1000; % 采样频率 T 1/Fs; % 采样周期&#xff1a;0.001s L 1500; % 信号长度 t (0:L-1)*T; % 时间向量. 时间向量从0开始递增&#xff0c;0s~1.499sS 0.7*sin(2*pi*50*t) sin(2*pi*120*t); % 模拟原信号 X S 2*randn(size(t)); …...

编程日记 2023/9/12 9:51:43

Python|合并两个字典的几种方法

在Python中&#xff0c;有多种方法可以通过使用各种函数和构造函数来合并字典。在本文中&#xff0c;我们将讨论一些合并字典的方法。 1. 使用方法update() 通过使用Python中的update()方法&#xff0c;可以将一个列表合并到另一个列表中。但是在这种情况下&#xff0c;第二个…...

编程日记 2023/9/12 9:50:42

ElementUI浅尝辄止24：Message 消息提示

常用于主动操作后的反馈提示。与 Notification 的区别是后者更多用于系统级通知的被动提醒。 1.如何使用&#xff1f; Message 在配置上与 Notification 非常类似&#xff0c;所以部分 options 在此不做详尽解释&#xff0c;可以结合 Notification 的文档理解它们。Element 注…...

编程日记 2023/9/12 9:49:40

在软件开发中正确使用MySQL日期时间类型的深度解析

在日常软件开发场景中&#xff0c;时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志&#xff0c;到供应链系统的物流节点时间戳&#xff0c;时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库&#xff0c;其日期时间类型的…...

编程新知 2025/10/16 13:22:06

golang循环变量捕获问题​​

在 Go 语言中&#xff0c;当在循环中启动协程&#xff08;goroutine&#xff09;时&#xff0c;如果在协程闭包中直接引用循环变量&#xff0c;可能会遇到一个常见的陷阱 - ​​循环变量捕获问题​​。让我详细解释一下&#xff1a; 问题背景 看这个代码片段&#xff1a; fo…...

编程新知 2026/1/21 14:29:57

【JavaEE】-- HTTP

1. HTTP是什么&#xff1f; HTTP&#xff08;全称为"超文本传输协议"&#xff09;是一种应用非常广泛的应用层协议&#xff0c;HTTP是基于TCP协议的一种应用层协议。 应用层协议&#xff1a;是计算机网络协议栈中最高层的协议&#xff0c;它定义了运行在不同主机上…...

编程新知 2026/1/26 21:34:05

day52 ResNet18 CBAM

在深度学习的旅程中&#xff0c;我们不断探索如何提升模型的性能。今天&#xff0c;我将分享我在 ResNet18 模型中插入 CBAM&#xff08;Convolutional Block Attention Module&#xff09;模块&#xff0c;并采用分阶段微调策略的实践过程。通过这个过程&#xff0c;我不仅提升…...

编程新知 2025/11/9 1:27:18

2.Vue编写一个app

1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

编程新知 2026/1/24 21:15:37

k8s业务程序联调工具-KtConnect

概述 原理 工具作用是建立了一个从本地到集群的单向VPN&#xff0c;根据VPN原理&#xff0c;打通两个内网必然需要借助一个公共中继节点&#xff0c;ktconnect工具巧妙的利用k8s原生的portforward能力&#xff0c;简化了建立连接的过程&#xff0c;apiserver间接起到了中继节…...

编程新知 2026/1/30 13:45:30

智能仓储的未来：自动化、AI与数据分析如何重塑物流中心

当仓库学会“思考”&#xff0c;物流的终极形态正在诞生 想象这样的场景&#xff1a; 凌晨3点&#xff0c;某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径&#xff1b;AI视觉系统在0.1秒内扫描包裹信息&#xff1b;数字孪生平台正模拟次日峰值流量压力…...

编程新知 2026/1/15 4:58:08

docker 部署发现spring.profiles.active 问题

报错&#xff1a; org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

编程新知 2025/9/20 12:14:18

七、数据库的完整性

七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

编程新知 2026/1/25 11:10:36

为什么要创建 Vue 实例

核心原因：Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为，将它们变成一个活的、可交互的应用**。没有这个实例，你的代码只是一堆静态的 HTML、JavaScript 变量和函数，无法「活」起来。 …...

编程新知 2026/1/3 7:21:08