蓝桥杯官网练习题(纸牌三角形)
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
A,2,3,4,5,6,7,8,9 共 99 张纸牌排成一个正三角形(A 按 1 计算)。要求每个边的和相等。 下图就是一种排法。
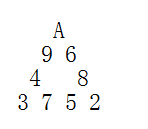
这样的排法可能会有很多。
如果考虑旋转、镜像后相同的算同一种,一共有多少种不同的排法呢?
请你计算并提交该数字。
运行限制
- 最大运行时间:1s
- 最大运行内存: 128M
//旋转和镜像后有六种情况可视为一种结果,所以结果除以6
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改public class Main {static int ans=0;static int[] a=new int[9];static int[] ans1=new int[9];static int[] biaoji=new int[10];public static void main(String[] args) {dfs(0);System.out.println(ans/6);}public static void dfs(int n){if(n==9){int a1=a[0]+a[1]+a[2]+a[3];int a2=a[3]+a[4]+a[5]+a[6];int a3=a[6]+a[7]+a[8]+a[0];if(a1==a2&&a2==a3){ans++;return;}else{return;}}if(a[n]!=0){dfs(n+1);}for(int i=1;i<=9;i++){if(a[n]==0&&biaoji[i]==0){a[n]=i;biaoji[i]=1;dfs(n+1);a[n]=0;biaoji[i]=0;}}}
}相关文章:

蓝桥杯官网练习题(纸牌三角形)
题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 A,2,3,4,5,6,7,8,9 共 99 张纸牌排成一个正三角形(A 按 1 计算)。要求每个边的和相等。 下图就是一种排法。 这样的排法可能会有很多。 如果…...

一辆新能源汽车的诞生之旅:比亚迪常州工厂探营
作为在新能源汽车领域首屈一指的国产品牌,比亚迪近年来可以说是捷报频传,高奏凯歌。 以比亚迪常州工厂为例,据介绍该工厂当初规划设计时定下的生产目标,是年产量能够达到20万辆。然而在2023年上半年,该工厂光是主要销往…...

【算法专题突破】双指针 - 最大连续1的个数 III(11)
目录 1. 题目解析 2. 算法原理 3. 代码编写 写在最后: 1. 题目解析 题目链接:1004. 最大连续1的个数 III - 力扣(Leetcode) 这道题不难理解,其实就是求出最长的连续是1的子数组, 但是,他支…...

java实现备忘录模式
备忘录模式是一种行为设计模式,它允许您捕获一个对象的内部状态,并在稍后的时间点将其恢复。这对于需要撤销操作或恢复到先前状态的应用程序非常有用。以下是在 Java 中实现备忘录模式的一般步骤: 创建一个原发器类(Originator&am…...
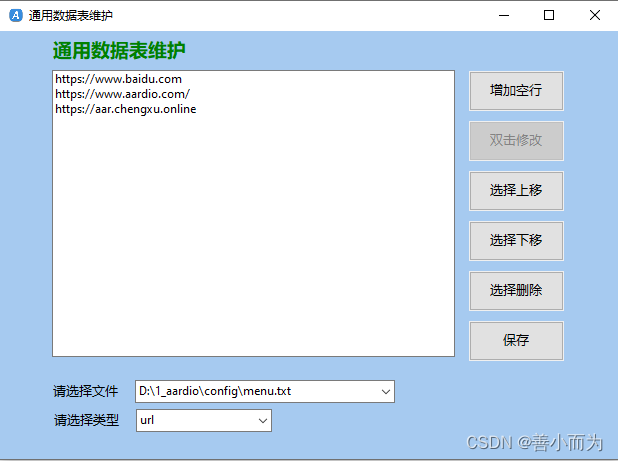
aardio语言的通用数据表维护
import win.ui; /*DSG{{*/ var winform win.form(text"通用数据表维护";right617;bottom427;bgcolor15780518) winform.add( buttonAdd{cls"button";text"增加空行";left469;top40;right564;bottom80;flat1;z2}; buttonDel{cls"button&quo…...

手写RPC框架--7.封装响应
RPC框架-Gitee代码(麻烦点个Starred, 支持一下吧) RPC框架-GitHub代码(麻烦点个Starred, 支持一下吧) 封装响应 封装响应a.封装响应b.请求id生成器(雪花算法)c.抽象序列化d.建立序列化工厂e.hessian的序列化方式(拓展) 封装响应 a.封装响应 在core模块…...
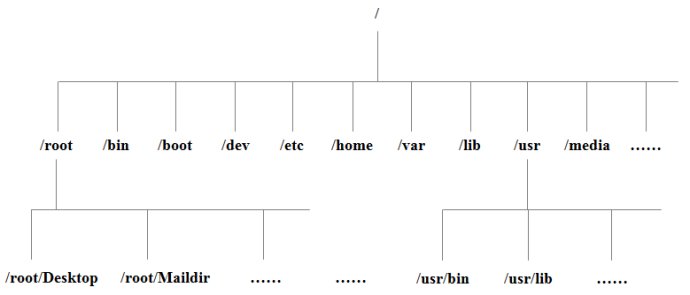
Linux入门教程||Linux系统目录结构
登录系统后,在当前命令窗口下输入命令: ls / 你会看到如下图所示: 树状目录结构: 以下是对这些目录的解释: /bin: bin是Binary的缩写, 这个目录存放着最经常使用的命令。 /boot: 这里存放的是启动Linux时…...

LeetCode 88. 合并两个有序数组
文章目录 一、题目二、C# 题解 一、题目 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。 注意&a…...
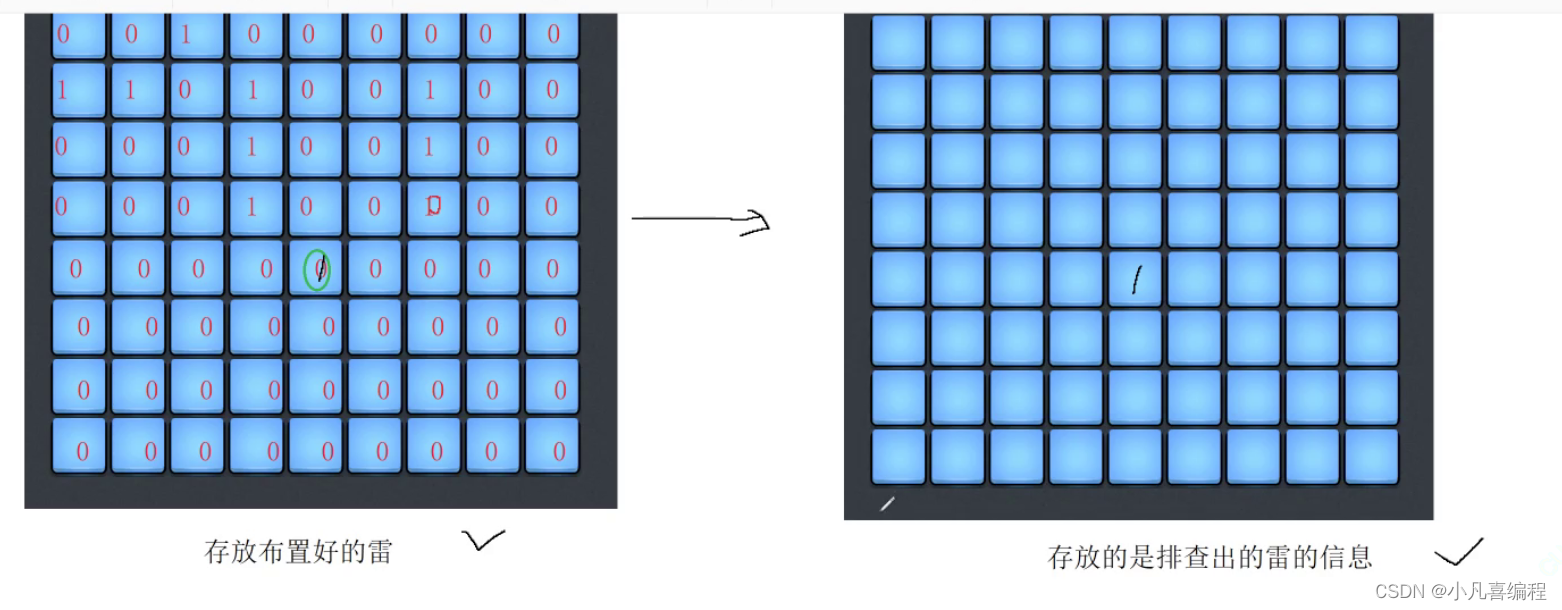
C语言实现扫雷小游戏
1.首先扫雷游戏要存储布置好的雷信息,需要一个二维数组 不是雷放* 雷:# 不是雷:0 雷:1 2. 给2个二维数组 9*9 一个存放雷的信息,一个存放布置好雷的信息 3.为了防止在统计坐标周围的…...
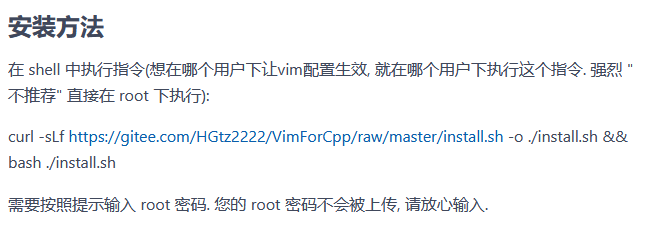
【linux基础(五)】Linux中的开发工具(上)---yum和vim
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:Linux从入门到开通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学更多操作系统知识 🔝🔝 Linux中的开发工具 1. 前言2.…...

C++学习之list的实现
在了解学习list实现之前我们首先了解一下关于迭代器的分类: 按功能分类: 正向迭代器 反向迭代器 const正向迭代器 const反向迭代器 按性质分类: 单向迭代器 只能 例如单链表 双向迭代器 可,也可-- 例如双…...

一种高效且节约内存的聚合数据结构的实现
一种高效且节约内存的聚合数据结构的实现 在特定的场景中,特殊定制数据结构能够得到更加好的性能且更节约内存。 聚合函数GroupArray的问题 GroupArray聚合函数是将分组内容组成一个个数组,例如下面的例子: SELECT groupArray(concat(ABC…...

机器学习(10)---特征选择
文章目录 一、概述二、Filter过滤法2.1 过滤法说明2.2 方差过滤2.3 方差过滤对模型影响 三、相关性过滤3.1 卡方过滤3.2 F检验3.3 互信息法3.4 过滤法总结 四、Embedded嵌入法4.1 嵌入法说明4.2 以随机森林为例的嵌入法 五、Wrapper包装法5.1 包装法说明5.2 以随机森林为例的包…...

Python之数据库(MYSQL)连接
一)数据库SQL语言基础 MySQL是一个关系型数据库管理系统,由瑞典MySQL AB 公司开发,目前属于 Oracle 旗下产品。MySQL 是最流行的关系型数据库管理系统之一,在 WEB 应用方面,MySQL是最好的 RDBMS (Relational Database…...
【建站教程】使用阿里云服务器怎么搭建网站?
使用阿里云服务器快速搭建网站教程,先为云服务器安装宝塔面板,然后在宝塔面板上新建站点,阿里云服务器网以搭建WordPress网站博客为例,阿小云来详细说下从阿里云服务器CPU内存配置选择、Web环境、域名解析到网站上线全流程&#x…...

【自然语言处理】关系抽取 —— MPDD 讲解
MPDD 论文信息 标题:MPDD: A Multi-Party Dialogue Dataset for Analysis of Emotions and Interpersonal Relationships 作者:Yi-Ting Chen, Hen-Hsen Huang, Hsin-Hsi Chen 期刊:LREC 2020 发布时间与更新时间:2020 主题:自然语言处理、关系抽取、对话场景、情感预测 数…...

深入理解JVM虚拟机第三篇:JVM的指令集架构模型和JVM的生命周期
文章目录 一:JVM的指令集架构模型 1:基于栈式架构的特点...

[小尾巴 UI 组件库] 组件库配置与使用
文章归档于:https://www.yuque.com/u27599042/row3c6 组件库地址 npm:https://www.npmjs.com/package/xwb-ui?activeTabreadme小尾巴 UI 组件库源码 gitee:https://gitee.com/tongchaowei/xwb-ui小尾巴 UI 组件库测试代码 gitee:…...
函数的理解)
Linux系统中fork()函数的理解
fork() 函数是一个在Unix和类Unix操作系统中常见的系统调用,用于创建一个新的进程,该进程是调用进程(父进程)的副本。fork() 函数的工作原理如下: 1. 当父进程调用 fork() 时,操作系统会创建一个新的进程&a…...
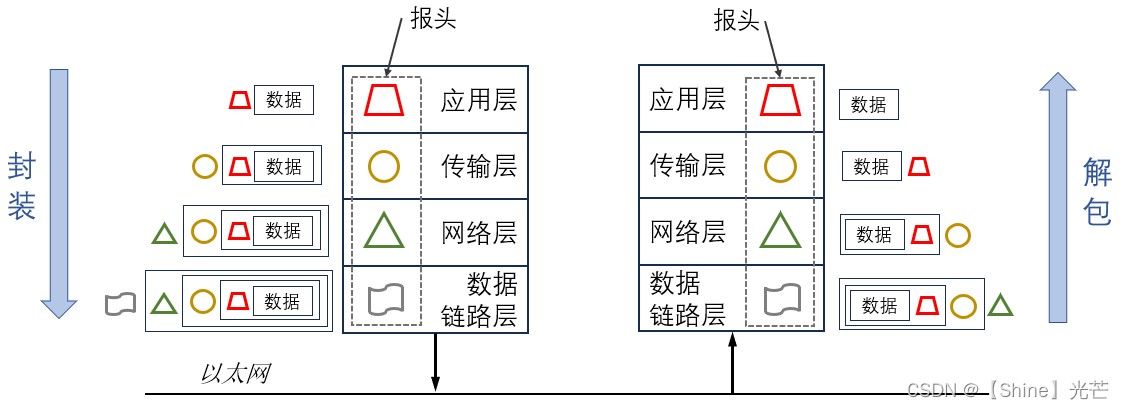
Linux网络编程:网络协议及网络传输的基本流程
目录 一. 计算机网络的发展 二. 网络协议的认识 2.1 对于协议分层的理解 2.2 TCP/IP五层协议模型 2.3 OSI七层模型 三. 网络传输的流程 3.1 同一网段中计算机通信的流程 3.2 不同网段中计算机设备的通信 3.3 对于IP地址和MAC地址的理解 3.4 数据的封装和解包 四. 总结…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
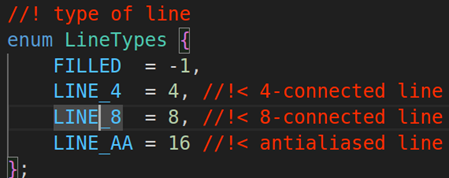
OPENCV图形计算面积、弧长API讲解(1)
一.OPENCV图形面积、弧长计算的API介绍 之前我们已经把图形轮廓的检测、画框等功能讲解了一遍。那今天我们主要结合轮廓检测的API去计算图形的面积,这些面积可以是矩形、圆形等等。图形面积计算和弧长计算常用于车辆识别、桥梁识别等重要功能,常用的API…...
