ROM是什么? 刷ROM是什么意思?
文章目录
- ROM是什么?
- 刷ROM是什么意思
ROM是什么?
ROM是只读内存(Read-Only Memory)的简称,是一种只能读出事先所存数据的固态半导体存储器。其特性是一旦储存资料就无法再将之改变或删除。通常用在不需经常变更资料的电子或电脑系统中,并且资料不会因为电源关闭而消失。
如今安卓智能手机说的最多还是刷机,但现在又冒出了一个刷ROM,对于很多朋友来说,容易将这两者混淆,以致于不容易理解。其实手机刷ROM就是指刷机。ROM是指手机硬盘(存储东西与系统文件的)。这里理解就好了,其实手机刷机就和电脑重装系统一样,可以让手机恢复到出厂原始系统状态,将系统盘重新安装一次。不过对于手机来说ROM最好不能刷大。
刷ROM是什么意思
专业的说,ROM是英文Read only Memory的缩写,中文意为只读存储器。顾名思义,就是手机的存储设备,它与手机RAM(内存)一样可以随时读和写。不过它只允许在生产出来之后有一次写的机会,数据一旦写入则不可更改。它另外一个特点是存储器掉电后里面的数据不丢失,可以存放成百上千年。手机ROM指的是存放手机固件代码的存储器(常说的刷机也就是指的是重新构建自己想要的ROM),比如手机的操作系统、一些应用程序如游戏等。
在手机中,RAM是指手机内存,对于手机看性能来说,除了看手机处理器就是看内存了,内存越大手机配置越好,目前主流手机均为1G内存(RAM),比较高端的手机则搭配了2G内存,由于技术限制,目前市场中还没有看到有4GB内存手机。而手机ROM是指手机存储器,比如手机内存SD卡就属于ROM范畴,用来存储手机系统文件、图片、音乐、照片等。ROM越大手机可以存储的东西就越大,目前一般主流手机存储为16GB,更高的有32G、64G,容量越大,一般手机也越贵,很多手机同一型号不同版本都是由ROM容量来划分的。
一个完整的ROM 根目录会有以下几个文件夹及文件: data、 META-IN、 system、 boot.img 四个文件夹 (data)是用户安装应用程序所在目录 ,(META-IN)是系统相关信息所在目录,一般定制一个ROM修改系统版本信息都在这里面。(system)为系统所在目录,相当于PC系统的Windows文件夹, (boot.img)是一个镜像文件,就是所谓的内核核心,一般移植ROM的时候会用到。手机ROM是储存手机操作系统的地方,一般情况下为了手机系统的安全是不允许被擦写的,因此操作系统储存在ROM中只能被读取而不能被更改擦写。
刷ROM是指通过一定的方法更改或替换了手机原版系统中固有的一些语言、图片、铃声和软件版本或者操作系统,可以使手机功能更加完善,类似于电脑中的重装系统。刷ROM都带有一定的风险,首先肯定的是,正常的刷ROM操作是不会损坏手机硬件的,其次刷ROM可以解决手机有些莫名其妙的毛病、升级手机硬件驱动(就象升级电脑的BIOS)、为手机增加无数DIY功能。但是不当的刷ROM方法可能带来不必要的麻烦,比如无法开机、开机死机、功能失效等后果。
编后语:一般刷ROM后就不保修了,所以要保修还是要刷机就要看个人权衡了。安卓手机刷ROM重装系统并没有什么风险,并不会像传说中的会使手机变砖或是坏掉,即使刷机失败,或是ROM不合适,只需再换个ROM重新刷一次即可,介绍到这里,相信大家对刷ROM已经完全了解了吧。
相关文章:

ROM是什么? 刷ROM是什么意思?
文章目录 ROM是什么?刷ROM是什么意思 ROM是什么? ROM是只读内存(Read-Only Memory)的简称,是一种只能读出事先所存数据的固态半导体存储器。其特性是一旦储存资料就无法再将之改变或删除。通常用在不需经常变更资料的…...
华为云Stack的学习(五)
六、华为云stack服务简介 1.云服务在华为云Stack中的位置 云服务对接多个数据中心资源池层提供的资源,并向各种行业应用提供载体。 2.华为云Stack通用服务 2.1 云计算的服务模式 2.2 计算相关的云服务 2.3 存储相关的云服务 2.4 网络相关的云服务 3.云化案例 **…...

【LeetCode-中等题】904. 水果成篮
文章目录 题目方法一:滑动窗口方法二: 题目 题目的意思就是:找至多包含两种元素的最长子串,返回其长度 方法一:滑动窗口 class Solution { // 滑动窗口 找至多包含两种元素的最长子串,返回其长度public …...
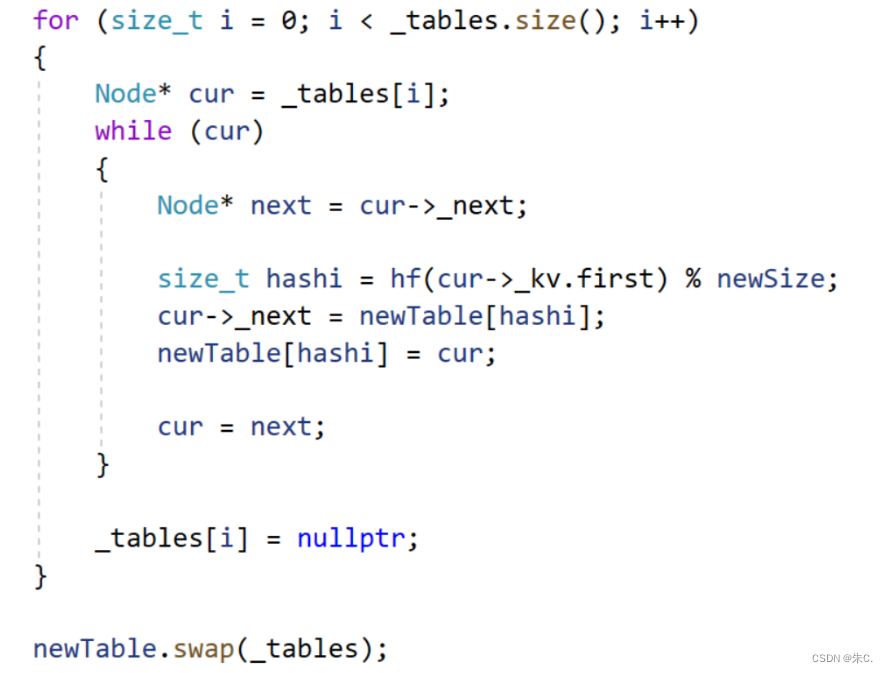
【C++】哈希——哈希的概念,应用以及闭散列和哈希桶的模拟实现
前言: 前面我们一同学习了二叉搜索树,以及特殊版本的平衡二叉搜索树,这些容器让我们查找数据的效率提高到了O(log^2 N)。虽然效率提高了很多,但是有没有一种理想的方法使得我们能提高到O(1)呢?其实在C语言数据结构中&a…...

Kubernetes (K8s) 解读:微服务与容器编排的未来
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🐅🐾猫头虎建议程序员必备技术栈一览表📖: 🛠️ 全栈技术 Full Stack: 📚…...
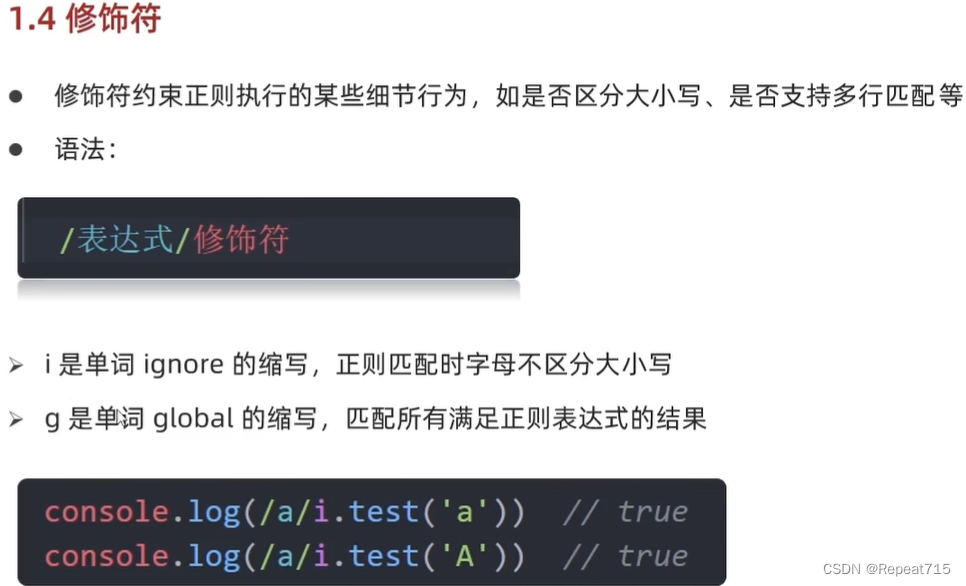
JavaScript学习--Day04
元字符 边界符: /^/:以什么开头 /$/:以什么结尾 量词: 预定义类:...
)
HCS 基本概念(三)
一、定义 HCS采用FusionSphere OpenStack作为云平台,对各个物理数据中心资源做整合,采用ManageOne作为数据中心管理软件对多个数据中心提供统一管理,通过云平台和数据中心管理软件协同运作,达到多数据中心融合、提升企业整体IT效率…...
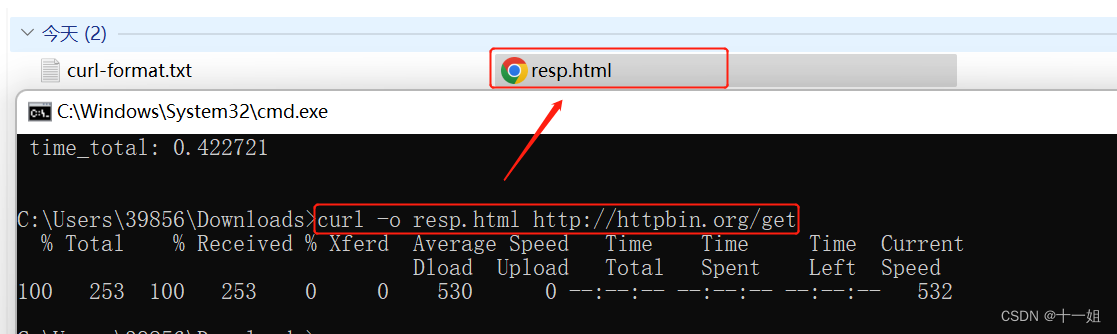
通过curl命令分析http接口请求各阶段的耗时等
目录 一、介绍二、功能1、-v 输出请求 响应头状态码 响应文本等信息2、-x 测试代理ip是否能在该网站使用3、-w 额外输出查看接口请求响应的消耗时间4、-o 将响应结果存储到文件里面5、-X post请求测试 (没测成功用的不多) 一、介绍 Curl是一个用于发送和接收请求的命令行工具和…...

Linux工具——gcc
目录 一,gcc简介 二,C语言源文件的编译过程 1.预处理 2.编译 3.汇编 4.链接 5.动静态库 一,gcc简介 相信有不少的小白和我一样在学习Linux之前只听说过visual studio。其实这个gcc这个编译器实现的功能便是和visual studio一样的功能&…...

uni-app 使用uCharts-进行图表展示(折线图带单位)
前言 在uni-app经常是需要进行数据展示,针对这个情况也是有人开发好了第三方包,来兼容不同平台展示 uCharts和pc端的Echarts使用差不多,甚至会感觉在uni-app使用uCharts更轻便,更舒服 但是这个第三方包有优点就会有缺点…...
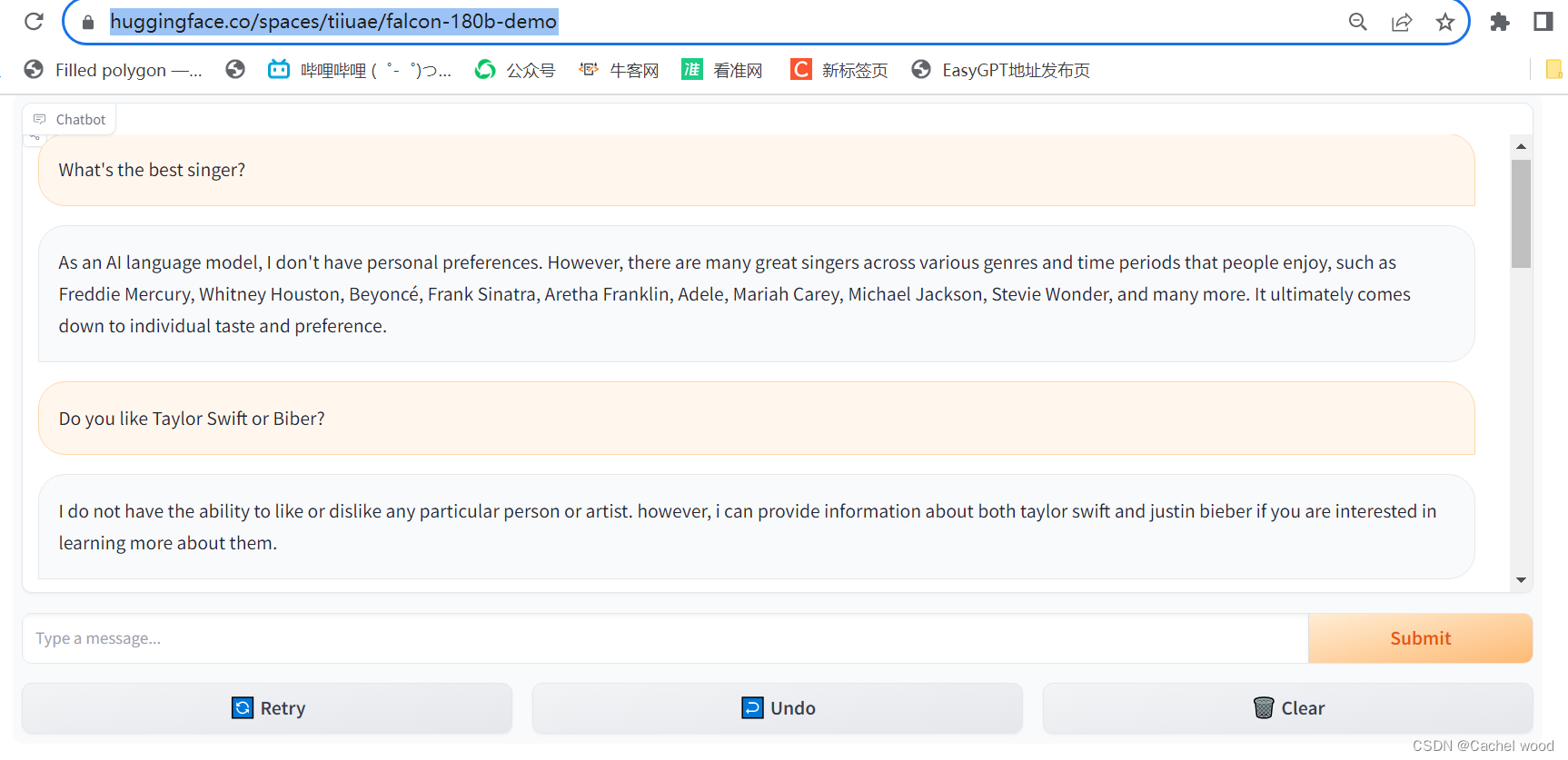
180B参数的Falcon登顶Hugging Face,vs chatGPT 最好开源大模型使用体验
文章目录 使用地址使用体验test1:简单喜好类问题test2:知识性问题test3:开放性问题test4:中文支持test5:问题时效性test6:学术问题使用地址 https://huggingface.co/spaces/tiiuae/falcon-180b-demo 使用体验 相比Falcon-7b,Falcon-180b拥有1800亿的参数量...
服务器数据恢复-EMC存储磁盘损坏的RAID5数据恢复案例
服务器数据恢复环境: 北京某单位有一台EMC某型号存储,有一组由10块STAT硬盘组建的RAID5阵列,另外2块磁盘作为热备盘使用。RAID5阵列上层只划分了一个LUN,分配给SUN小机使用,上层文件系统为ZFS。 服务器故障࿱…...

Nginx优化文件上传大小限制
Nginx默认配置 Nginx 默认情况下,上传文件的大小为1M,超过1M就会返回413错误。只用对Nginx进行简单配置即可解决问题。 优化Nginx文件上传大小限制 可以在Nginx配置文件中配置 client_max_body_size 配置项。 设置客户端请求正文允许的最大大小。如果…...
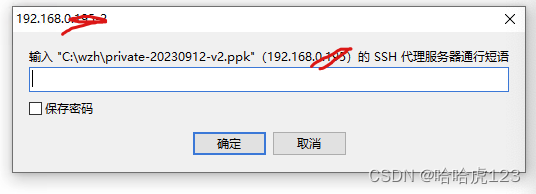
navicat SSH连接数据库报错: Putty key format too new
问题 下载 Putty 0.79 生成了密钥,但是在navicat 15 使用SSH通道连接数据库报错: Putty key format too new 错误原因和处理 原来是因为生成的私钥格式是 V3 , navicat 15 只能识别 V2 所以,在 PuTTYgen Load 私钥,重新保存为 …...
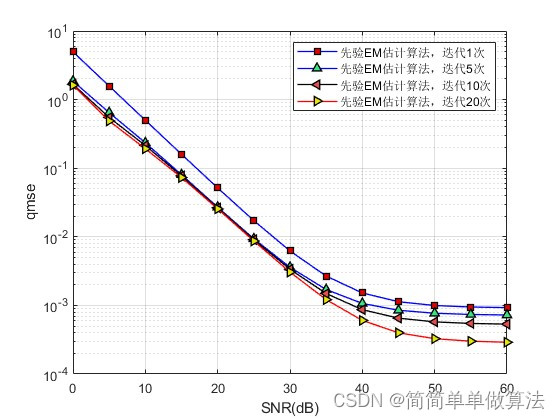
基于大规模MIMO通信系统的半盲信道估计算法matlab性能仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 %EM算法收敛所需的迭代 nIter 1; Yp Y(:,1:L_polit,:); %与导频序列相对应的部分 q…...
———— OVV Recall Rate与 IV Recall Rate)
自然语言处理学习笔记(九)———— OVV Recall Rate与 IV Recall Rate
目录 1.OVV Recall Rate 2. IV Recall Rate 1.OVV Recall Rate OOV指的是“未登录词”(Out Of Vocabulary),或者俗称的“新词”,也即词典未收录的词汇。如何准确切分00V,乃至识别其语义,是整个NLP领域的核…...

区块链正在开启一场回归商业,融合商业的新发展
对于区块链来讲,它其实同样在延续着这样一种发展路径。 正如上文所说,区块链正在开启一场回归商业,融合商业的新发展。 而欲要实现这一点,区块链就是要从底层算法,底层数据传输,底层体系的打造着手…...

【软考】系统集成项目管理工程师(三)信息系统集成专业技术知识③
一、云计算 1、定义 通过互联网来提供大型计算能力和动态易扩展的虚拟化资源;云是网络、互联网的一种比喻说法。是一种大集中的服务模式。 2、特点 (1)超大规模(2)虚拟化(3)高可扩展性&…...

js中如何判断一个对象是否为空对象?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 使用 Object.keys()⭐ 使用 for...in 循环⭐ 使用 JSON.stringify()⭐ 使用 ES6 的 Object.getOwnPropertyNames()⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带…...

Linux SysRq 简介
文章目录 1. 前言2. 背景3. Linux SysRq3.1 SysRq 简介3.1.1 SysRq 初始化 3.2 通过 procfs 发起 SysRq 请求3.2.1 修改内核日志等级3.2.1.1 触发3.2.1.2 实现简析 3.2.2 手动触发内核 panic3.2.2.1 触发3.2.2.2 实现简析3.2.2.3 应用场景 3.2.3 其它 SysRq 请求 3.3 通过 特殊…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
