如何理解图神经网络的傅里叶变换和图卷积
图神经网络(GNN)代表了一类强大的深度神经网络架构。在一个日益互联的世界里,因为信息的联通性,大部分的信息可以被建模为图。例如,化合物中的原子是节点,它们之间的键是边。
图神经网络的美妙之处在于它们能够在不牺牲重要细节的情况下直接对图结构数据进行操作。这一点在处理复杂的数据集(如化合物)时尤为明显,GNN使我们能够充分利用底层图形表示的丰富性。通过这样做,GNN能够更全面地理解原子和键之间的关系,从而为更准确和深入的分析开辟途径。

在化学领域之外,图结构的影响延伸到不同的领域。以交通数据为例,其中城市是节点,它们之间的路线是边。GNN在交通堵塞预测等任务中被证明是非常宝贵的,证明了它们在捕捉城市流动性的复杂动态方面是有效的。当面临预测交通拥堵等挑战时,GNN掌握图数据中固有的空间依赖性和模式的能力成为一种强有力的工具。基于GNN的众多模型已成为预测交通拥堵的最先进解决方案,成为最前沿的模型。下面是paperswithcode上预测交通堵塞的模型,基本上全部是GNN 本文将介绍图卷积的理论基础。通过深入研究图傅立叶变换的复杂性及其与图卷积的联系,我们将为深入理解GNN世界中的这一关键概念奠定基础。
本文将介绍图卷积的理论基础。通过深入研究图傅立叶变换的复杂性及其与图卷积的联系,我们将为深入理解GNN世界中的这一关键概念奠定基础。
如何定义图卷积
GNN的核心概念在于图卷积,通过捕获节点和边之间的关系,实现对图数据的有效处理。在理解图卷积的各种方法中,本文侧重于利用图傅里叶变换的理论来进行解释。这个概念提供了一个深入研究图卷积的机制的独特视角。图傅里叶变换允许我们用图形频率来表示图形信号——与节点相关的数据。这种以光谱分析为基础的分解,提供了对图中潜在模式和结构的洞察。一些GNN架构利用注意力机制和其他超越图卷积范围的高级方法。但是我们主要探讨图卷积的本质及其与图傅立叶变换的相互作用,所以注意力等部分不在本文的范围内
什么是图傅里叶变换?
图傅里叶变换的概念与经典的傅里叶变换有着有趣的相似之处。就像传统的傅里叶变换将一个波信号分解成它的组成频率一样,图傅里叶变换在图结构数据进行操作,揭示嵌入其中的信号的频率。想象一个没有环路或多个边缘结构的加权无向图。图傅里叶变换是一种数学运算,它强调了图上存在的信号的变换。在信号维数等于1的情况下,这个概念变得特别具有说明性。考虑下面的描述,它描绘了信号在图表上的样子[1]。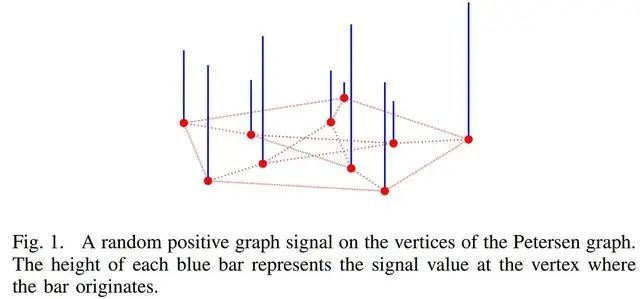 将信号分解为图的频率,或图傅里叶变换,提供了一种识别图形数据中固有的各种关系、规律和复杂性的方法。
将信号分解为图的频率,或图傅里叶变换,提供了一种识别图形数据中固有的各种关系、规律和复杂性的方法。
图拉普拉斯算子
为了理解图的傅里叶变换,我们将开始一个基本的探索,首先介绍图的拉普拉斯变换。这个关键概念是揭示图形固有频率特性的基石。图拉普拉斯量记为L,定义为: 在这个等式中,A表示邻接矩阵,它编码了图中节点之间的连接,D表示度矩阵,捕获每个节点的度。由于D和A是实对称矩阵,因此图拉普拉斯矩阵也具有实对称矩阵的性质。这个性质使我们能够对图拉普拉斯函数进行谱分解,表示为:
在这个等式中,A表示邻接矩阵,它编码了图中节点之间的连接,D表示度矩阵,捕获每个节点的度。由于D和A是实对称矩阵,因此图拉普拉斯矩阵也具有实对称矩阵的性质。这个性质使我们能够对图拉普拉斯函数进行谱分解,表示为: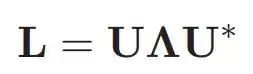 上式中,U表示特征向量矩阵,Λ是由特征值(Λ 1, Λ 2,…,Λ n)组成的对角矩阵。
上式中,U表示特征向量矩阵,Λ是由特征值(Λ 1, Λ 2,…,Λ n)组成的对角矩阵。
二次形
本节解释了拉普拉斯图的二次形和二次形的含义,以及它如何与图信号的频率联系起来。图拉普拉斯的二次型可以定义为: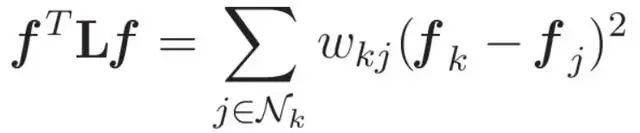 这里的f表示图信号,w表示一条边的权值,Nk表示与节点k相连的节点集。这个表示形式揭示了两个基本的关键方面:函数的平滑性二次型提供了对函数在图形上的平滑性的洞察。考虑f =[1,1,1,…,1]T的场景。根据图拉普拉斯式的定义,二次型的计算结果为零。也就是说,函数在节点间越平滑,得到的二次型就越小。这种相互作用提供了一种机制来量化图形信号固有的平滑程度。相邻节点之间的相似性二次型也用作评估相邻节点上信号之间相似性的度量。当f(i)与f(j)相差较大时,对应的二次型值成比例增大。相反,如果相邻节点上的信号相似,则二次型趋近于零。这种观察结果与二次型值越大反映相邻节点之间变化越大的想法是一致的。有了这些概念,二次型就可以被解释为图形上函数“频率”的替代物。通过利用它提供信息,我们可以进行基于频率成分的图形信号分解。这一关键步骤是图傅里叶变换的先驱,解锁了一种强大的方法来揭示嵌入在图结构数据中的频率特征。
这里的f表示图信号,w表示一条边的权值,Nk表示与节点k相连的节点集。这个表示形式揭示了两个基本的关键方面:函数的平滑性二次型提供了对函数在图形上的平滑性的洞察。考虑f =[1,1,1,…,1]T的场景。根据图拉普拉斯式的定义,二次型的计算结果为零。也就是说,函数在节点间越平滑,得到的二次型就越小。这种相互作用提供了一种机制来量化图形信号固有的平滑程度。相邻节点之间的相似性二次型也用作评估相邻节点上信号之间相似性的度量。当f(i)与f(j)相差较大时,对应的二次型值成比例增大。相反,如果相邻节点上的信号相似,则二次型趋近于零。这种观察结果与二次型值越大反映相邻节点之间变化越大的想法是一致的。有了这些概念,二次型就可以被解释为图形上函数“频率”的替代物。通过利用它提供信息,我们可以进行基于频率成分的图形信号分解。这一关键步骤是图傅里叶变换的先驱,解锁了一种强大的方法来揭示嵌入在图结构数据中的频率特征。
图傅里叶变换
我们已经建立了拉普拉斯图的二次形作为信号频率的指示器,其中二次形值越大表示频率越高。还有一个要点是:要注意这些值可能受到f的范数的影响。为了确保一致性并消除不同范数的潜在影响,我们还需要施加f的范数等于1的约束。为了得到范数条件下二次型的平稳值,我们利用了拉格朗日乘子法这一强大的优化技术。对该问题进行适当的变换,最终得到一个特征值问题: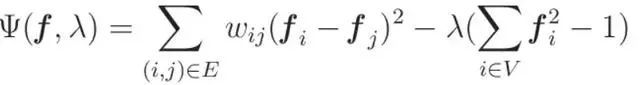
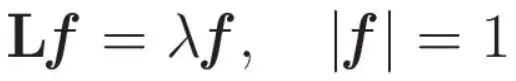 这个特征值提供了一个关系:L的每个特征值反映了图拉普拉斯的二次形的值。简单地说,这些特征值捕获了图形信号振动的频率。这样我们对特征值作为函数频率的指标有了基本的理解。特征向量和图拉普拉斯之间的联系成为进行图傅立叶变换的途径——一个系统地揭示图信号内在频率元素的过程。现在,我们可以看看傅里叶变换的定义了
这个特征值提供了一个关系:L的每个特征值反映了图拉普拉斯的二次形的值。简单地说,这些特征值捕获了图形信号振动的频率。这样我们对特征值作为函数频率的指标有了基本的理解。特征向量和图拉普拉斯之间的联系成为进行图傅立叶变换的途径——一个系统地揭示图信号内在频率元素的过程。现在,我们可以看看傅里叶变换的定义了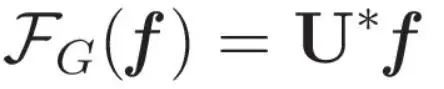
从图傅里叶变换到图卷积
上面介绍的图傅里叶变换,我们获得了一个有效分析和处理图信号的强大工具。在我们研究图傅里叶变换和图卷积之间的联系。这种联系的核心是卷积定理,这个原理建立了傅里叶域中卷积运算和元素积之间的联系。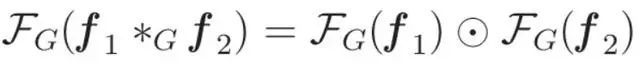 卷积运算类似于傅里叶域中变换后的信号的逐元乘法。利用卷积定理可以推导图卷积的一个间接定义:
卷积运算类似于傅里叶域中变换后的信号的逐元乘法。利用卷积定理可以推导图卷积的一个间接定义:
- 对图形信号进行傅里叶变换。
- 将变换后的信号与一个可学习的权重向量相乘。
- 对元素积进行傅里叶反变换,得到图卷积的输出。
图卷积的公式现在可以表述如下: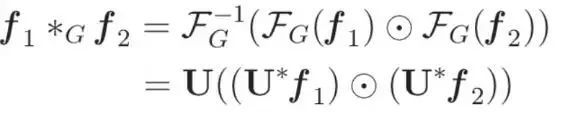 为了使这个定义更加精简,我们引入了一个实用的参数化。由于与U*f的元素积可以表示为与diag(U*f)的积,s所以设可学习权值θ为:
为了使这个定义更加精简,我们引入了一个实用的参数化。由于与U*f的元素积可以表示为与diag(U*f)的积,s所以设可学习权值θ为: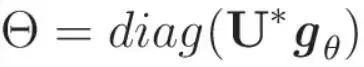 通过利用这种参数化,gθ的图卷积公式采用了一种简化和直观的形式:
通过利用这种参数化,gθ的图卷积公式采用了一种简化和直观的形式: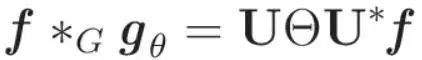 看看,我们已经从图的傅里叶变换中定义了一个图卷积!
看看,我们已经从图的傅里叶变换中定义了一个图卷积!
总结
在本文中,我们从揭示图拉普拉斯的基本原理开始,然后深入研究了图卷积的基本概念,这是图傅里叶变换的推导。本文中所做的推到应该能够加深了你对图卷积本质的理解。
相关文章:
如何理解图神经网络的傅里叶变换和图卷积
图神经网络(GNN)代表了一类强大的深度神经网络架构。在一个日益互联的世界里,因为信息的联通性,大部分的信息可以被建模为图。例如,化合物中的原子是节点,它们之间的键是边。图神经网络的美妙之处在于它们能…...

国家网络安全周2023时间是什么时候?有什么特点?谁举办的?
国家网络安全周2023时间是什么时候? 2023年国家网络安全宣传周将于9月11日至17日在全国范围内统一开展。其中开幕式等重要活动将在福建省福州市举行。今年网安周期间,除开幕式外,还将举行网络安全博览会、网络安全技术高峰论坛、网络安全微视…...
windows编程之线程同步万字总结(创建线程,互斥对象,互斥事件,信号量,关键段,多线程群聊服务器)
文章目录 创建线程方法一_beginthreadex函数讲解使用示例: 方法二CreateThread函数讲解:使用示例: 互斥对象:创建互斥对象CreateMutex 互斥事件介绍创建或打开一个未命名的互斥事件对象 信号量介绍信号量的相关函数使用示例 关键段相关函数错误使用示例正确使用示例…...
)
Git在已有的项目中引入Submodule子模块管理:添加、更新、删除(实战示例代码)
前言 在进行Git版本控制的过程中,有时候我们需要在已有的项目中引入子模块,以便复用其他独立的Git存储库的代码或文件。本文将详细介绍如何在已有项目下添加、更新和删除Git的Submodule子模块,并提供相关的示例代码。 实战场景 假设我们已…...
内网穿透实现Windows远程桌面访问Ubuntu,简单高效的远程桌面解决方案
文章目录 前言1. ubuntu安装XRDP2.局域网测试连接3.安装cpolar内网穿透4.cpolar公网地址测试访问5.固定域名公网地址 前言 XRDP是一种开源工具,它允许用户通过Windows RDP访问Linux远程桌面。 除了Windows RDP外,xrdp工具还接受来自其他RDP客户端(如Fre…...

如何学习运营管理
运营管理(Operations Management)是一门管理学科,它关注如何高效地组织和管理企业的生产、服务、供应链和业务过程以达到组织的目标。运营管理是企业管理的一个重要领域,它包含了多个内容和职能: 生产管理:…...

腾讯云centos7.6安装部署备忘
1.Mysql 1.1 安装mysql wget http://dev.mysql.com/get/mysql-community-release-el7-5.noarch.rpm rpm -ivh mysql-community-release-el7-5.noarch.rpm yum install mysql-community-server 1.1.1 安装后重启 service mysqld restart 1.1.2 初次安装mysql,root账…...

【赠书活动】考研备考书单推荐
👉博__主👈:米码收割机 👉技__能👈:C/Python语言 👉公众号👈:测试开发自动化【获取源码商业合作】 👉荣__誉👈:阿里云博客专家博主、5…...

中缀表达式 - 栈实现综合计算器
代码: package Algotithm.stackobject Calculator {def main(args: Array[String]): Unit {val expression "32*6-2"//创建两个栈:数栈、符号栈val numStack, operStack new ArrayStack2(10)//定义需要的相关变量var index, num1, num2, …...

html语音播报功能问题
语音播报有个问题,就是弹出层有时无法关闭页面的播报,如果弹出层也有语音播报,就会造成语音混者播放 解决办法就是在弹出窗口(我用的弹出层框架是layui的)之前清空语音 window.operEdit function (url, title){window.speechSynthesis.can…...
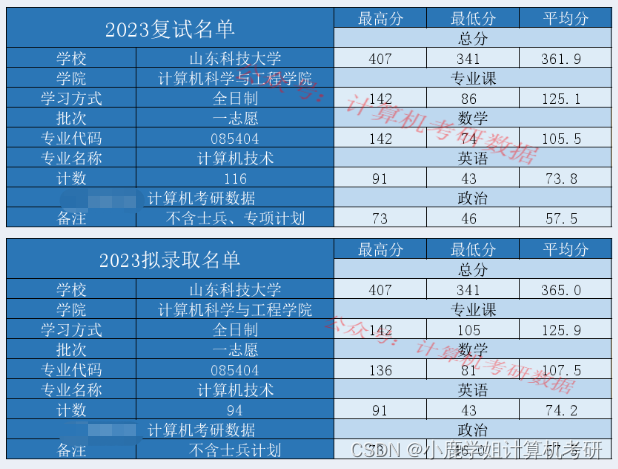
计算机重点学科评级B-,山东省属重点高校考情分析
山东科技大学(B-) 考研难度(☆☆) 内容:23考情概况(拟录取和复试分析)、院校概况、23专业目录、23复试详情、各专业考情分析、各科目考情分析。 正文1175字预计阅读:3分钟 2023考情概况 山东科技大学计…...

轻松搭建本地知识库的ChatGLM2-6B
近期发现了一个项目,它的前身是ChatGLM,在我之前的博客中有关于ChatGLM的部署过程,本项目在前者基础上进行了优化,可以基于当前主流的LLM模型和庞大的知识库,实现本地部署自己的ChatGPT,并可结合自己的知识…...

flink的物理DataFlow图及Slot处理槽任务分配
背景 在flink中,有几个比较重要的概念,逻辑DataFlow图,物理DataFlow图以及处理槽执行任务,本文就来讲解下这几个概念 概念详解 假设有以下代码:数据源和统计单词算子的并行度是2,数据汇算子的并行度是1&…...

与面试相关的redis
这里写自定义目录标题 📝 redis的知识点数据结构及其特性,用途和操作方法持久化高可用分布式锁发布订阅性能优化安全性数据分片缓存策略键过期删除策略内存淘汰策略 🤗 总结归纳📎 参考文章 😀 这里写文章的前言&#…...

MapStruct从0到0.5
MapStruct从0到0.5 开发的过程,经常会用到实体类属性映射,同时为了方便,开发者也很少自己写专门的属性赋值工具类。索性会直接使用Sprrng提供的BeanUtils工具类,然后在性能上和字段属性赋值上的问题,一直是为开发者所…...
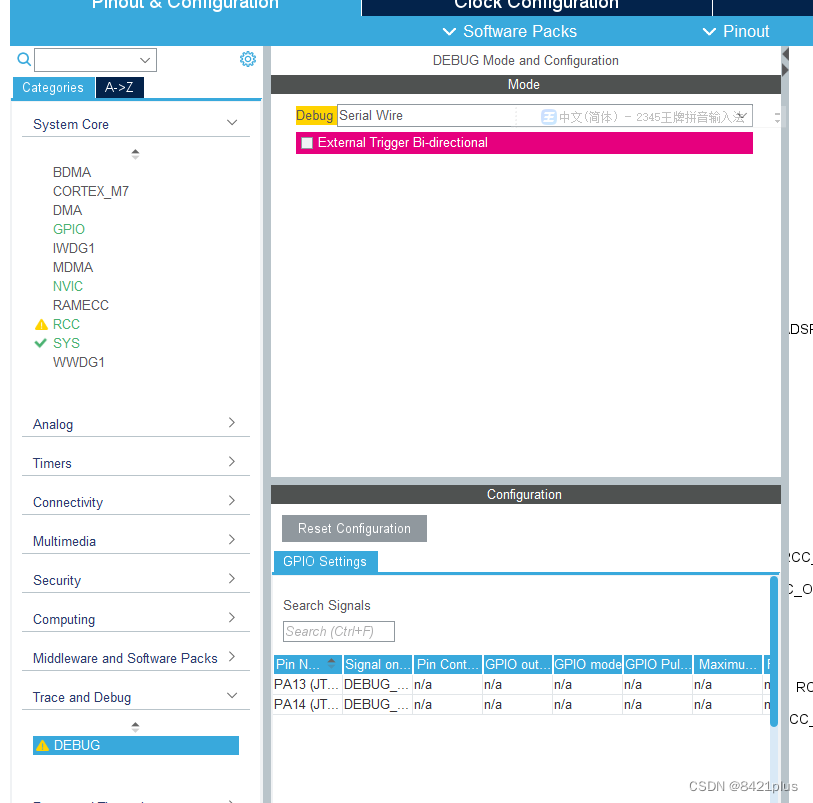
STM32H750 HAL CUBEMX 时钟失败及死机无法下载问题解决
芯片采样电压设置,否则 无法运行 解决死机问题 设置swd 模式 短接 boot0 —vcc 3.3v即可正常下载...

paddlespeech on centos7
概述 paddlespeech是百度飞桨平台的开源工具包,主要用于语音和音频的分析处理,其中包含多个可选模型,提供语音识别、语音合成、说话人验证、关键词识别、音频分类和语音翻译等功能。 paddlespeech整体是比较简单易用的,但是安装…...

ROM是什么? 刷ROM是什么意思?
文章目录 ROM是什么?刷ROM是什么意思 ROM是什么? ROM是只读内存(Read-Only Memory)的简称,是一种只能读出事先所存数据的固态半导体存储器。其特性是一旦储存资料就无法再将之改变或删除。通常用在不需经常变更资料的…...
华为云Stack的学习(五)
六、华为云stack服务简介 1.云服务在华为云Stack中的位置 云服务对接多个数据中心资源池层提供的资源,并向各种行业应用提供载体。 2.华为云Stack通用服务 2.1 云计算的服务模式 2.2 计算相关的云服务 2.3 存储相关的云服务 2.4 网络相关的云服务 3.云化案例 **…...

【LeetCode-中等题】904. 水果成篮
文章目录 题目方法一:滑动窗口方法二: 题目 题目的意思就是:找至多包含两种元素的最长子串,返回其长度 方法一:滑动窗口 class Solution { // 滑动窗口 找至多包含两种元素的最长子串,返回其长度public …...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...
