PYQT常用组件--方法汇总
QTimeEdit
timeEdit是Qt框架中的一个时间编辑器控件,它提供了以下常用方法:
- setTime(QTime time): 设置时间编辑器的时间为指定的QTime对象。
- time(): 返回时间编辑器的当前时间,返回一个QTime对象。
- setDateTime(QDateTime dateTime): 设置时间编辑器的日期和时间为指定的QDateTime对象。
- dateTime(): 返回时间编辑器的当前日期和时间,返回一个QDateTime对象。
- setFormat(const QString &format): 设置时间编辑器的日期和时间格式,以指定的字符串表示。
- format(): 返回时间编辑器的当前日期和时间格式的字符串表示。
- timeSpec(): 返回当前时间使用的时区规范,返回一个Qt::TimeSpec枚举值。
- setTimeSpec(Qt::TimeSpec spec): 设置时间编辑器的时区规范,以Qt::TimeSpec枚举值表示。
- calendarWidget(): 返回时间编辑器关联的日历控件,如果未关联则返回nullptr。
- setCalendarPopup(bool enable): 设置是否启用日历弹出菜单,用于快速选择日期。
- calendarPopup(): 返回是否启用日历弹出菜单。
- minimumTime(): 返回时间编辑器的最小可能时间。
- maximumTime(): 返回时间编辑器的最大可能时间。
- setMinimumTime(const QTime &time): 设置时间编辑器的最小可能时间为指定的时间。
- setMaximumTime(const QTime &time): 设置时间编辑器的最大可能时间为指定的时间。
- 这些方法可以用于获取和设置时间编辑器的属性,以及与日期和时间相关的操作。
相关文章:

PYQT常用组件--方法汇总
QTimeEdit timeEdit是Qt框架中的一个时间编辑器控件,它提供了以下常用方法: setTime(QTime time): 设置时间编辑器的时间为指定的QTime对象。time(): 返回时间编辑器的当前时间,返回一个QTime对象。setDateTime(QDateTime dateTime): 设置时…...

Linux系统编程(一):文件 I/O
参考引用 UNIX 环境高级编程 (第3版)黑马程序员-Linux 系统编程 1. UNIX 基础知识 1.1 UNIX 体系结构(下图所示) 从严格意义上说,可将操作系统定义为一种软件,它控制计算机硬件资源,提供程序运行环境,通常…...

OSM+three.js打造3D城市
对于我在 Howest 的研究项目,我决定构建一个 3D 版本的 Lucas Bebber 的“交互式讲故事的动画地图路径”项目。我将使用 OSM 中的矢量轮廓来挤出建筑物的形状并将它们添加到 3js 场景中,随后我将对其进行动画处理。 一、开发环境 为了使用 Node 和 npm 包,我选择使用 Vite…...

02JVM_垃圾回收GC
二、垃圾回收GC 在堆里面存放着java的所有对象实例,当对象为“死去”,也就是不再使用的对象,就会进行垃圾回收GC 1.如何判断对象可以回收 1.1引用计数器 介绍 在对象中添加一个引用计数器,当一个对象被其他变量引用时这个对象…...

ARM Linux DIY(八)USB 调试
前言 V3s 带有一个 USB 接口,将其设置为 HOST 或 OTG 模式,这样可以用来接入键盘、鼠标等 USB 外设。 USB 简介 USB 有两种设备:HOST 和 USB 功能设备。 在 USB2.0 中又引入了一个新的概念 OTG,即设备角色可以动态切换。 切换方…...

编程小白的自学笔记十四(python办公自动化创建、复制、移动文件和文件夹)
系列文章目录 编程小白的自学笔记十三(python办公自动化读写文件) 编程小白的自学笔记十二(python爬虫入门四Selenium的使用实例二) 编程小白的自学笔记十一(python爬虫入门三Selenium的使用实例详解) …...

MySQL使用Xtrabackup备份到AWS存储桶
1.安装Xtrabackup cd /tmp wget https://downloads.percona.com/downloads/Percona-XtraBackup-8.0/Percona-XtraBackup-8.0.33-28/binary/redhat/7/x86_64/percona-xtrabackup-80-8.0.33-28.1.el7.x86_64.rpm yum -y localinstall percona-xtrabackup-80-8.0.33-28.1.el7.x86…...
Redis 7 第11讲 BIGKEY 优化篇)
(高阶)Redis 7 第11讲 BIGKEY 优化篇
面试题 问题答案如何在海量数据中查询某一固定前缀的Keyscan生产环境如何限制 keys */FLUSHDB/FLUSHALL 等危险命令,防止误删误用# 修改配置文件 rename-command keys "" rename-command flushdb "" rename-command flushall ""如何使用MEMORY U…...

一阶差分和二阶差分概念及其举例
一阶差分和二阶差分概念及其举例 目录 一阶差分和二阶差分概念及其举例1、一阶差分1.1 概念1.2 举例 2、二阶差分2.1 概念2.2 举例 1、一阶差分 1.1 概念 一阶差分是指对一个数列中的每个元素,计算其与其前一个元素之差的操作。 1.2 举例 举例来说,对…...
使用自定义注解和SpringAOP捕获Service层异常,并处理自定义异常
目录 一 自定义异常二 自定义注解三 注解切面处理类四 使用 一 自定义异常 /*** 自定义参数为null异常*/ public class NoParamsException extends Exception {//用详细信息指定一个异常public NoParamsException(String message){super(message);}//用指定的详细信息和原因构…...
Kotlin(六) 类
目录 创建类 调用类 类的继承------open 构造函数 创建类 创建类和创建java文件一样,选择需要创建的目录New→Kotlin File/Class Kotlin中也是使用class关键字来声明一个类的,这一点和Java一致。现在我们可以在这个类中加入字段和函数来丰富它的功…...
)
蓝桥杯官网练习题(灌溉)
题目描述 小蓝负责花园的灌溉工作。 花园可以看成一个 n 行 m 列的方格图形。中间有一部分位置上安装有出水管。 小蓝可以控制一个按钮同时打开所有的出水管,打开时,有出水管的位置可以被认为已经灌溉好。 每经过一分钟,水就会向四面扩展…...
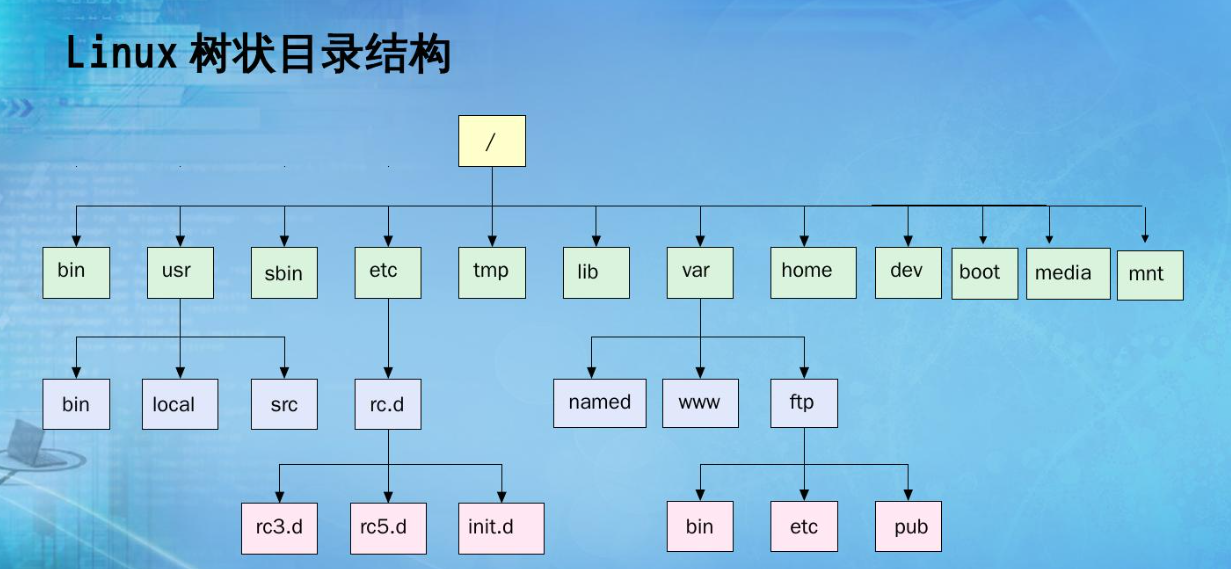
数据结构:树的概念和结构
文章目录 1. 树的概念2. 树的结构3. 树的相关概念4. 树的表示孩子表示法双亲表示法孩子兄弟表示法 5. 树在实际中的应用5. 树在实际中的应用 1. 树的概念 树是一种非线性的数据结构,它是由 n (n > 0)个有限结点组成一个具有层次关系的. 把它叫做树是因为它看起来像一棵倒挂的…...

【GIS】栅格转面报错:ERROR 000864输入栅格: 输入不在定义的属性域内。 ERROR 000863: 无效的 GP 数据类型
问题: 栅格转面(矢量)时,ArcGIS窗口显示:ERROR 000864输入栅格: 输入不在定义的属性域内。 ERROR 000863: 无效的 GP 数据类型. 原因: 栅格转面时输入的栅格数据集的字段必须是整型. 解决办法: 使用Spatial Analyst中的转为整型工具,将栅格数据转为整型后再进行栅格转面的操作…...

32 WEB漏洞-文件操作之文件下载读取全解
目录 介绍利用获取数据库配置文件文件名,参数值,目录符号 涉及案例:Pikachu-文件下载测试-参数Zdns-文件下载真实测试-功能点小米路由器-文件读取真实测试-漏洞RoarCTF2019-文件读取真题复现-比赛百度杯2017二月-Zone真题复现-比赛拓展 下载和读取都差不…...

Linux之history、tab、alias、命令执行顺序、管道符以及exit
目录 Linux之history、tab、alias、命令执行顺序、管道符以及exit history历史命令 格式 参数 修改默认记录历史命令条数 案例 案例1 --- 显示history历史记录中出现次数最高的top10 案例2 --- 增加history显示的时间信息 命令与文件名补全 --- tab 命令别名 格式 案…...

vcomp100.dll丢失怎样修复?5个靠谱的修复方法分享
VCOMP100.DLL 是由微软打造的动态链接库,它对于一些图形密集型应用,例如Photoshop,以及多款知名游戏如巫师3的运行至关重要。 如果操作系统在启动应用程序时无法找到此vcomp100.dll,则会出现vcomp100.dll丢失或未找到错误。 如果D…...
)
Vue3自定义指令(directive)
文章目录 前言一、Vue3指令钩子函数二、自定义指令的两种方式1.局部使用例子1:鉴权例子2:拖拽 2.全局使用例子1:监听宽高指令例子2:监听是否出现在视口 总结 前言 此文章主要讲了vue3中自定义指令的使用,以及一些WebA…...

大数据课程L9——网站流量项目的实时业务处理代码
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 掌握网站流量项目的SparkStreaming代码; ⚪ 掌握网站流量项目的HBaseUtil代码; ⚪ 掌握网站流量项目的MysqlUtil代码; ⚪ 掌握网站流量项目的LogBean代码; ⚪ 掌握网站流量项目的To…...
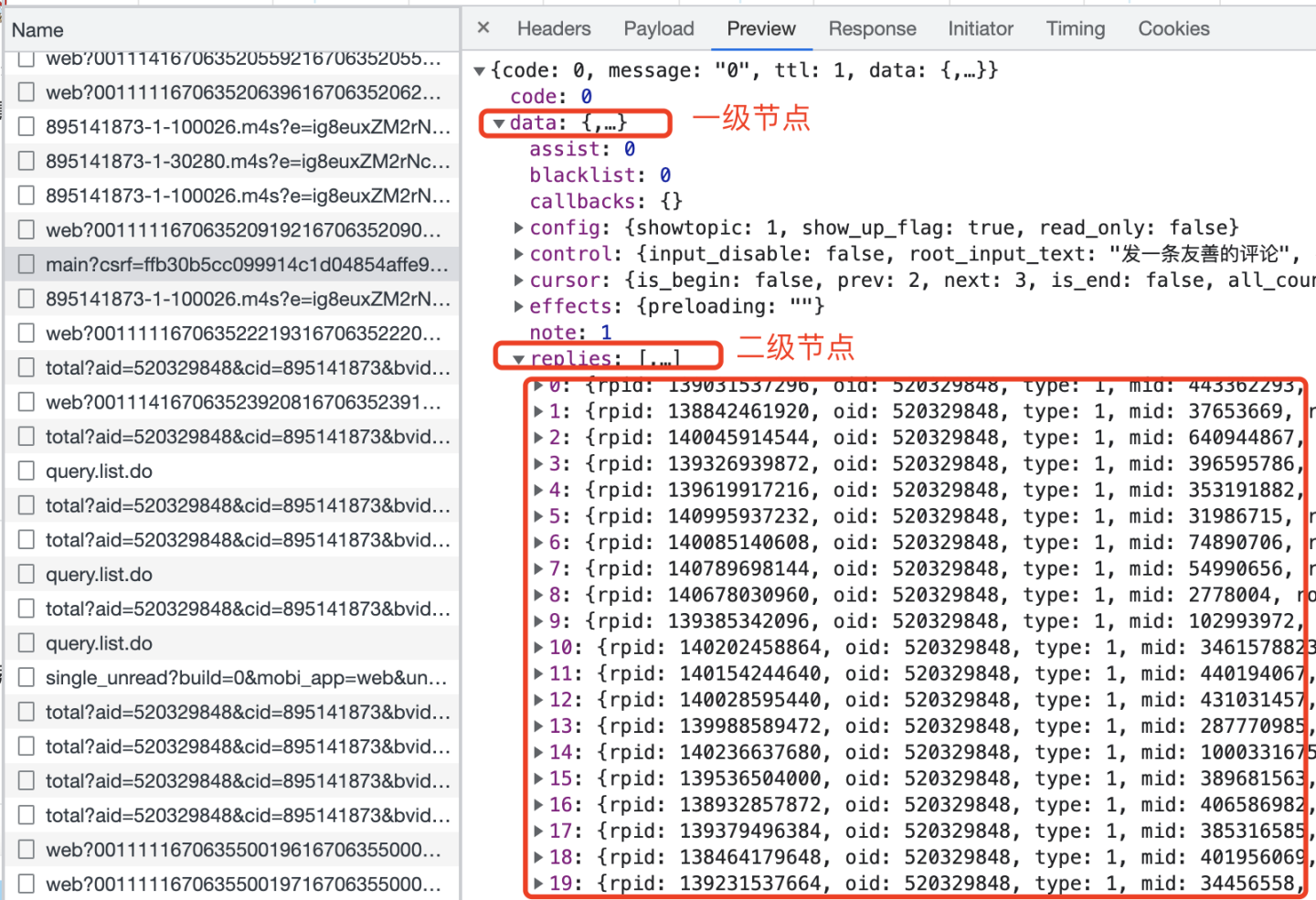
【2023最新B站评论爬虫】用python爬取上千条哔哩哔哩评论
文章目录 一、爬取目标二、展示爬取结果三、爬虫代码四、同步视频五、附完整源码 您好,我是 马哥python说,一枚10年程序猿。 一、爬取目标 之前,我分享过一些B站的爬虫: 【Python爬虫案例】用Python爬取李子柒B站视频数据 【Pyt…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
