665. 非递减数列-先改后验法
665. 非递减数列
给你一个长度为 n 的整数数组 nums ,请你判断在 最多 改变 1 个元素的情况下,该数组能否变成一个非递减数列。
我们是这样定义一个非递减数列的: 对于数组中任意的 i (0 <= i <= n-2),总满足 nums[i] <= nums[i + 1]。
示例 1:
输入: nums = [4,2,3]
输出: true
解释: 你可以通过把第一个 4 变成 1 来使得它成为一个非递减数列。
示例 2:
输入: nums = [4,2,1]
输出: false
解释: 你不能在只改变一个元素的情况下将其变为非递减数列。
这题直接使用先改后验法就可以了,这种问题,基本都是这么做的,一次修改,检索是否符合条件。
解题代码如下:
bool checkPossibility(int* nums, int numsSize){for(int i=0;i<numsSize-1;i++){if(i>=1){if(nums[i]>nums[i+1]&&nums[i+1]>=nums[i-1]){nums[i]=nums[i+1];break;}if(nums[i]>nums[i+1]&&nums[i+1]<nums[i-1]){nums[i+1]=nums[i];break;}}if(i==0){if(nums[i]>nums[i+1]){nums[i]=nums[i+1];break;}}}for(int i=0;i<numsSize-1;i++){printf("%d ",nums[i]);}for(int i=0;i<numsSize-1;i++){if(nums[i]>nums[i+1]){return false;}}return true;}
相关文章:

665. 非递减数列-先改后验法
665. 非递减数列 给你一个长度为 n 的整数数组 nums ,请你判断在 最多 改变 1 个元素的情况下,该数组能否变成一个非递减数列。 我们是这样定义一个非递减数列的: 对于数组中任意的 i (0 < i < n-2),总满足 nums[i] < …...
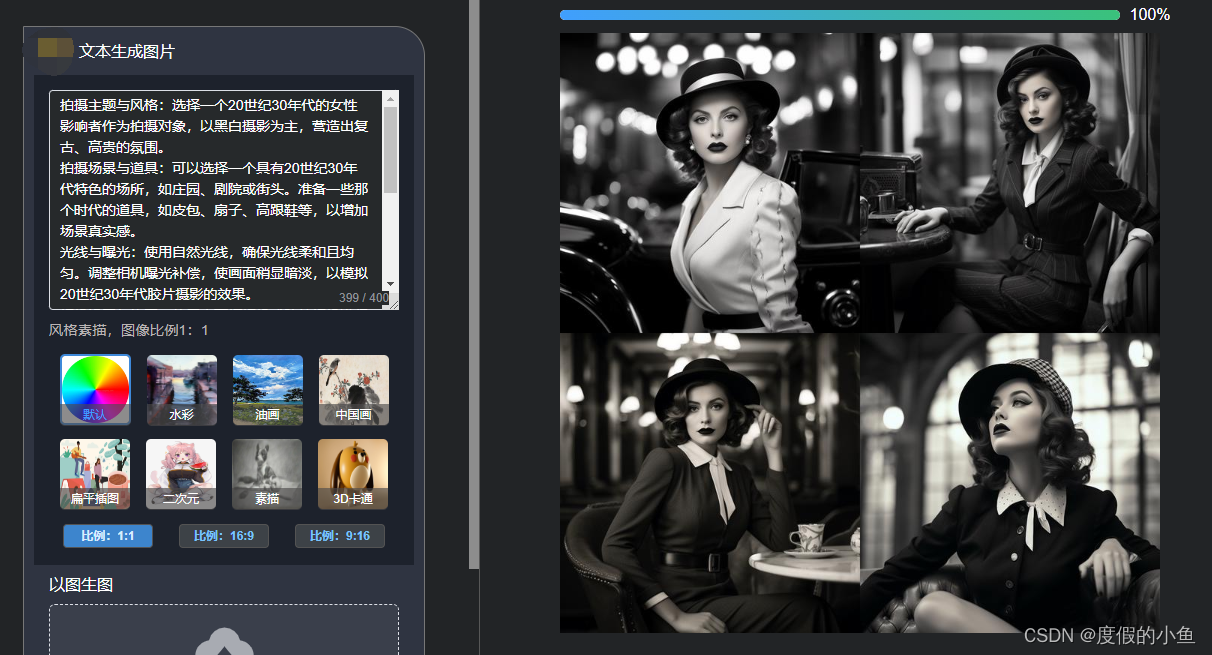
调教 文心一言 生成 AI绘画 提示词(Midjourney)
文章目录 第一步第二步第三步第四步第五步第六步第七步第八步 文心一言支持连续对话 我瞎玩的非专业哈哈 第一步 你好,今天我们要用扩散模型创建图像。我会给你提供一些信息。行吗? 第二步 这是Midjourney的工作原理:Midjourney是另一个基于ai的工具,能…...
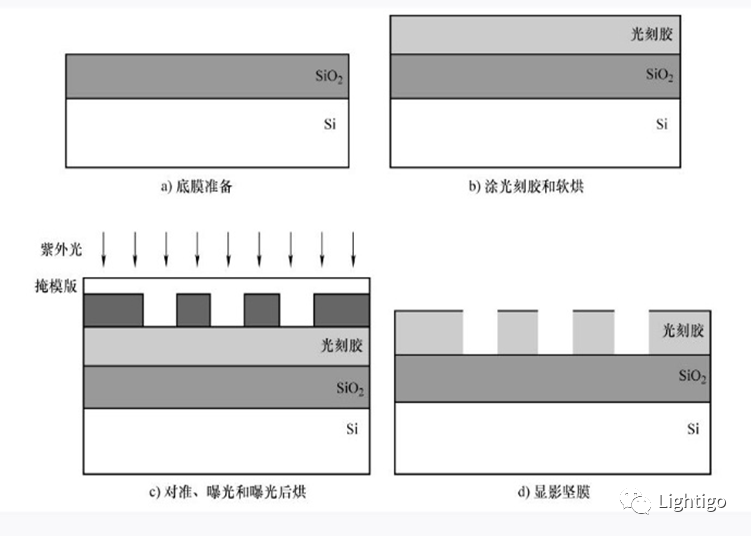
半导体制造工艺(一)光刻
在这里开个新专题,主要详细描述半导体制造整个流程中所用到的设备工艺步骤。 在集成电路制造工艺中,光刻是决定集成器件集成度的核心工序,该工序的作用是将图形信息从掩模版(也称掩膜版)上保真传输、转印到半导体材料衬…...

【海思SS626 | 开发环境】VMware17安装Ubuntu 18.04.6
目录 一、下载 Ubuntu 18.04.6 LTS二、VMware17创建虚拟机三、安装Ubuntu18.04LTS四、安装其他软件五、总结 一、下载 Ubuntu 18.04.6 LTS 问题:为什么要下载 Ubuntu18.04.6 LTS 而不是使用最新的,或者其他Linux发行版? 答:在ss6…...
每天10个小知识点)
Vue知识系列(3)每天10个小知识点
目录 系列文章目录Vue知识系列(1)每天10个小知识点Vue知识系列(2)每天10个小知识点 知识点**21. Vue不同生命周期**的概念、作用、原理、特性、优点、缺点、区别、使用场景**22. Vue 子组件和父组件执行顺序****23. created 和 mo…...

Java基础入门·多线程·线程池ThreadPool篇
前言 特点分析 线程池ThreadPool 销毁线程池 Executor类 Callable接口 线程池使用 …...

Trinitycore学习之在vscode查看远端服务器上源码配置
1:安装vscode,去官网下载,这里下载windows版本安装包 .zip https://code.visualstudio.com/Download 2:安装后,安装扩展chinese,使用中文设置,需要重启vscode。 3:安装ssh相关插件…...

583. 两个字符串的删除操作 -- 动规
583. 两个字符串的删除操作 class MinDistance:"""583. 两个字符串的删除操作https://leetcode.cn/problems/delete-operation-for-two-strings/description/"""def solution(self, text1: str, text2: str) -> int:"""这道题…...
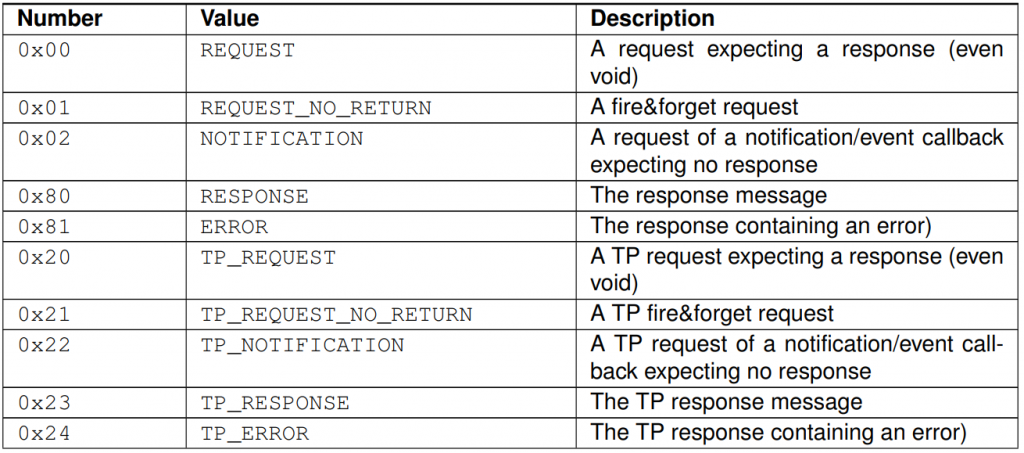
SOME/IP
介绍 SOME/IP是一种汽车中间件解决方案,可用于控制消息。它从一开始就被设计为完美地适应不同尺寸和不同操作系统的设备。这包括小型设备,如相机、AUTOSAR 设备,以及头戴设备或远程通信设备。它还确保SOME/IP支持信息娱乐域以及车辆中其他域…...

[2023.09.12]: Yew应用开发的第一个hook--use_state
Yew的SSR模式推荐使用function_component组件,并且在function_component中使用hooks。其中,我使用到的第一个hook是use_state。use_state的设计意图与React中的useState非常相似,都是为了保存并修改当前的状态。然而,由于Yew是用R…...

使用Langchain+GPT+向量数据库chromadb 来创建文档对话机器人
使用LangchainGPT向量数据库chromadb 来创建文档对话机器人 一.效果图如下: 二.安装包 pip install langchainpip install chromadbpip install unstructuredpip install jieba三.代码如下 #!/usr/bin/python # -*- coding: UTF-8 -*-import os # 导入os模块&…...
系列教程(一) 服务注册与发现(eureka))
Spring Cloud(Finchley版本)系列教程(一) 服务注册与发现(eureka)
Spring Cloud(Finchley版本)系列教程(一) 服务注册与发现(eureka) 为了更好的浏览体验,欢迎光顾勤奋的凯尔森同学个人博客http://www.huerpu.cc:7000 如有错误恳请大家批评指正,与大家共同学习、一起成长,万分感谢。 一、构建环境 Spring Cloud的构建工具可以使用Maven或Gr…...

【大数据】美团 DB 数据同步到数据仓库的架构与实践
美团 DB 数据同步到数据仓库的架构与实践 1.背景2.整体架构3.Binlog 实时采集4.离线还原 MySQL 数据5.Kafka2Hive6.对 Camus 的二次开发7.Checkdone 的检测逻辑8.Merge9.Merge 流程举例10.实践一:分库分表的支持11.实践二:删除事件的支持12.总结与展望 1…...
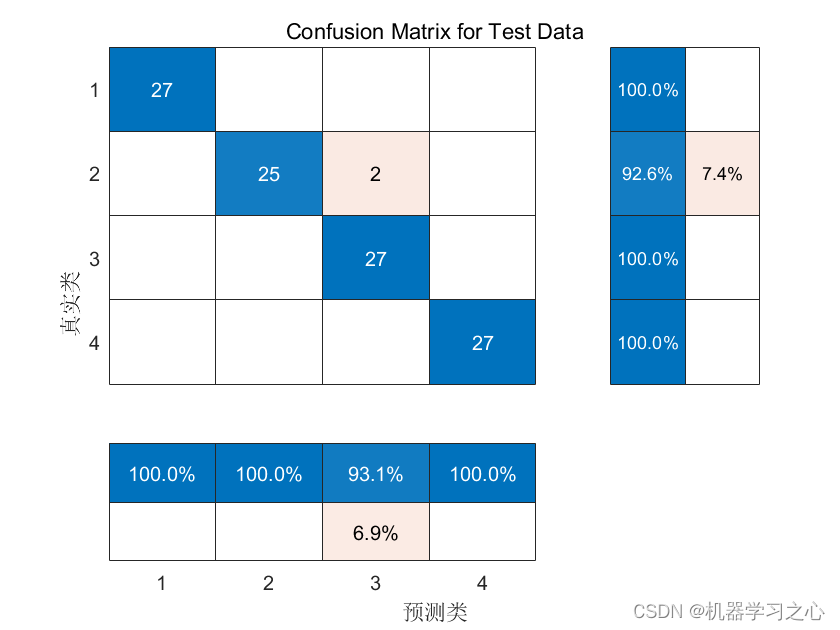
分类预测 | MATLAB实现WOA-CNN-BiGRU鲸鱼算法优化卷积双向门控循环单元数据分类预测
分类预测 | MATLAB实现WOA-CNN-BiGRU鲸鱼算法优化卷积双向门控循环单元数据分类预测 目录 分类预测 | MATLAB实现WOA-CNN-BiGRU鲸鱼算法优化卷积双向门控循环单元数据分类预测分类效果基本描述模型描述程序设计参考资料 分类效果 基本描述 1.Matlab实现WOA-CNN-BiGRU多特征分类…...
mac使用squidMan设置代理服务器
1,下载squidMan http://squidman.net/squidman/ 2, 配置SquidMan->Preference 3, mac命令窗口配置 export http_proxy export https_porxy 4,客户端配置(centos虚拟机) export http_proxyhttp://服务器ip:8080 export https…...

大数据Flink(七十八):SQL 的水印操作(Watermark)
文章目录 SQL 的水印操作(Watermark) 一、为什么要有 WaterMark...
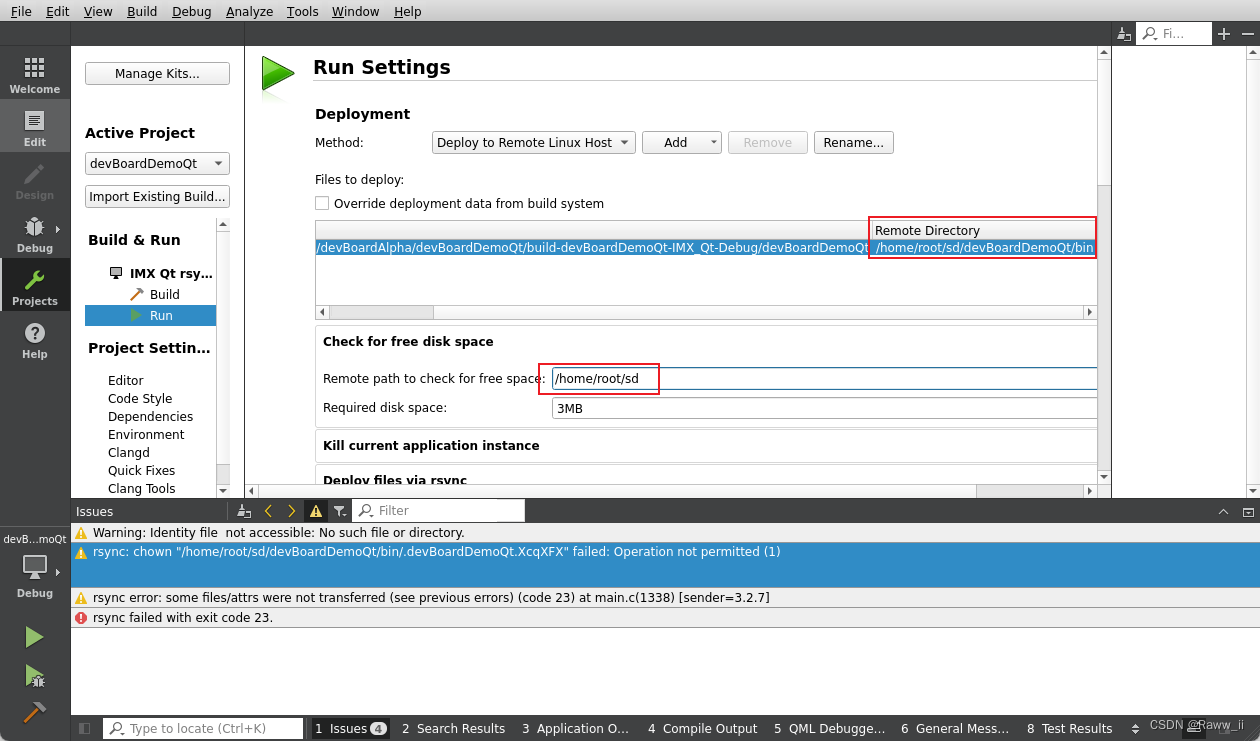
【Linux】Qt Remote之Remote开发环境搭建填坑小记
总体思路 基于WSL2(Ubuntu 22.04 LTS)原子Alpha开发板进行Qt开发实验,基于Win11通过vscode remote到WSL2,再基于WSL2通过Qt 交叉编译,并通过sshrsync远程到开发板,构建起开发工具链。 Step1 基于Win11通过…...

ATFX汇市:离岸人民币大幅升值,昨日盘中跌破7.3关口
ATFX汇市:美国CPI数据即将公布之际,周一美元指数大跌,带动离岸人民币升值0.85%,实现3月14日以来的最大单日升值幅度,当日汇率(USDCNH)最低触及7.292,突破7.3000关口。消息面上&#…...

Spring Boot 配置 Knife4j
一、引入 maven <!-- 引入 knife4j 文档--> <dependency> <groupId>com.github.xiaoymin</groupId> <artifactId>knife4j-openapi2-spring-boot-starter</artifactId> <version>4.1.0</version> </dependency>二…...

Java项目中遇到uv坐标如何转换成经纬度坐标
将UV坐标(通常指平面坐标,如二维地图坐标)转换为经纬度坐标(地理坐标)通常需要知道一个参考点的经纬度坐标,以及两者之间的比例关系。这是因为UV坐标通常用于在地图上绘制图形或标记点,而经纬度…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
