熵 | 无线通信知识
文章目录
- 一、信息论(熵、联合熵、条件熵)
- 二、Bernoulli熵
- 三、联合熵和条件熵
- 四、互信息
- 五、相对熵(KL距离)
- 六、微分熵
- 七、最大熵分布
- 常需要的不等式公式
一、信息论(熵、联合熵、条件熵)
熵定义: H ( X ) = E [ − l o g 2 p ( x ) ] = − ∑ x ∈ X p ( x ) l o g 2 p ( x ) H(X)=E[-log_2p(x)]=-\sum_{x\in X}p(x)log_2p(x) H(X)=E[−log2p(x)]=−x∈X∑p(x)log2p(x)
note
- H(X)是X的平均香农信息内容
- H(X)是每个符号的平均信息量
- 二元问题(抛硬币),H(X)取值为[H(X),H(X)+1]
为什么用 l o g 2 ( . ) log_2(.) log2(.)衡量信息
非负性: f ( p ) ≥ 0 f(p)\ge0 f(p)≥0, 0 ≤ p ≤ 1 0\le p\le1 0≤p≤1
特殊点:当p=0, f ( p ) = ∞ f(p)=\infty f(p)=∞
可加性
单调递增连续性 ??
二、Bernoulli熵
符号集 χ = [ 0 , 1 ] \chi=[0,1] χ=[0,1],对应的概率 p ⃗ = [ p , 1 − p ] \vec{p}=[p,1-p] p=[p,1−p]
Bernoulli熵: H ( X ) = H ( p ) = − p l o g 2 p − ( 1 − p ) l o g 2 ( 1 − p ) H(X)=H(p)=-plog_2p-(1-p)log_2(1-p) H(X)=H(p)=−plog2p−(1−p)log2(1−p)
note:
- 通常用 H ( p ) H(p) H(p)表示 H ( X ) H(X) H(X)
- p=0 or 1时, H ( p ) = 0 H(p)=0 H(p)=0
- H ( p ) H(p) H(p)是p的凸函数
- p=0.5, H ( p ) H(p) H(p)最大
- H ( p ) H(p) H(p)的取值范围 0 ≤ H ( p ) ≤ l o g 2 ∣ χ ∣ 0\le H(p)\le log_2|\chi| 0≤H(p)≤log2∣χ∣

三、联合熵和条件熵
联合熵:
H ( X , Y ) = − E l o g p ( x , y ) = − ∑ x ∈ X ∑ y ∈ Y p ( x , y ) l o g p ( x , y ) H(X,Y)=-Elogp(x,y)=-\sum_{x\in X} \sum_{y\in Y} p(x,y)logp(x,y) H(X,Y)=−Elogp(x,y)=−x∈X∑y∈Y∑p(x,y)logp(x,y)
条件熵
H ( Y ∣ X ) = − E l o g ( y ∣ x ) = − ∑ x ∈ X ∑ y ∈ Y p ( x , y ) l o g p ( y ∣ x ) H(Y|X)=-Elog(y|x)=-\sum_{x\in X} \sum_{y\in Y}p(x,y)logp(y|x) H(Y∣X)=−Elog(y∣x)=−x∈X∑y∈Y∑p(x,y)logp(y∣x)
H ( Y ∣ X ) = ∑ x ∈ X p ( x ) H ( Y ∣ X = x ) H(Y|X)=\sum_{x\in X}p(x)H(Y|X=x) H(Y∣X)=x∈X∑p(x)H(Y∣X=x)
熵的链式法则
- H ( X , Y ) = H ( X ) + H ( Y ∣ X ) H(X,Y)=H(X)+H(Y|X) H(X,Y)=H(X)+H(Y∣X)
- H ( X , Y ∣ Z ) = H ( X ∣ Z ) + H ( Y ∣ X , Z ) H(X,Y|Z)=H(X|Z)+H(Y|X,Z) H(X,Y∣Z)=H(X∣Z)+H(Y∣X,Z)
- H ( X 1 , X 2 , . . . . X n ) = ∑ i = 1 n H ( X i ∣ X i − 1 , . . . . X 1 ) H(X_1,X_2,....X_n)=\sum_{i=1}^{n}H(X_i|X_{i-1},....X_1) H(X1,X2,....Xn)=∑i=1nH(Xi∣Xi−1,....X1)
四、互信息
定义:
I ( X ; Y ) = H ( X ) − H ( X ∣ Y ) = H ( X ) + H ( Y ) − H ( X , Y ) I(X;Y)=H(X)-H(X|Y)=H(X)+H(Y)-H(X,Y) I(X;Y)=H(X)−H(X∣Y)=H(X)+H(Y)−H(X,Y)
互信息具有对称性
I ( X ; Y ) = H ( X ) − H ( X ∣ Y ) = H ( Y ) − H ( Y ∣ X ) I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X) I(X;Y)=H(X)−H(X∣Y)=H(Y)−H(Y∣X)
I ( X ; Y ) = H ( X ) + H ( Y ) − H ( X , Y ) I(X;Y)=H(X)+H(Y)-H(X,Y) I(X;Y)=H(X)+H(Y)−H(X,Y)
I ( X ; Y ) = I ( Y , X ) I(X;Y)=I(Y,X) I(X;Y)=I(Y,X)
I ( X ; X ) = H ( X ) I(X;X)=H(X) I(X;X)=H(X)
I ( X ; Y ) ≥ 0 I(X;Y)\ge0 I(X;Y)≥0,当且仅当X Y互相独立时,等号成立
互信息的链式法则
I ( X 1 , X 2 , . . . . X n ; Y ) = ∑ i = 1 n I ( X i ; Y ∣ X i − 1 , . . . . , X 1 ) I(X_1,X_2,....X_n;Y)=\sum_{i=1}^nI(X_i;Y|X_{i-1},....,X_1) I(X1,X2,....Xn;Y)=i=1∑nI(Xi;Y∣Xi−1,....,X1)
五、相对熵(KL距离)
D ( p ⃗ ∣ ∣ q ⃗ ) = ∑ x ∈ X p ( x ) l o g q ( x ) p ( x ) = E p ⃗ [ − l o g q ( x ) ] − H ( p ⃗ ) D(\vec{p}||\vec{q})=\sum_{x\in X}p(x)log\frac{q(x)}{p(x)}=E_{\vec{p}}[-logq(x)]-H(\vec{p}) D(p∣∣q)=x∈X∑p(x)logp(x)q(x)=Ep[−logq(x)]−H(p)
D ( p ⃗ ∣ ∣ q ⃗ ) D(\vec{p}||\vec{q}) D(p∣∣q)测量的是两个概率分布 p ⃗ \vec{p} p和 q ⃗ \vec{q} q间的距离,并非真实距离
D ( p ⃗ ∣ ∣ q ⃗ ) ≥ 0 D(\vec{p}||\vec{q})\ge 0 D(p∣∣q)≥0,当且仅当 p ⃗ \vec{p} p= q ⃗ \vec{q} q,等号成立
六、微分熵
对于连续型随机变量,一个以f(x)为密度函数的连续型随机变量,X的微分熵h(x)为:
h ( x ) = ∫ − ∞ ∞ f X ( x ) l o g f X ( x ) d x = E − l o g f X ( x ) h(x)=\int_{-\infty}^{\infty}f_X{(x)}logf_X(x)dx=E-logf_X(x) h(x)=∫−∞∞fX(x)logfX(x)dx=E−logfX(x)
note
- 微分熵仅依赖于随机变量的概率密度函数,有时候将微分熵写为h(f)
- 微分熵可以为负值
微分熵分类
| 均匀分布的微分熵 | 高斯分布的微分熵 | 多元高斯分布的微分熵 | |
|---|---|---|---|
| 前提条件:随机变量服从 | 均匀分布 X ∼ U ( a , b ) X\sim U(a,b) X∼U(a,b) | 高斯分布 X ∼ U ( μ , σ 2 ) X\sim U(\mu,\sigma^2) X∼U(μ,σ2) | X 1 : n ∼ N ( m ⃗ , k ⃗ ) X_{1:n}\sim N(\vec{m},\vec{k}) X1:n∼N(m,k) |
| f ( x ) = { 1 b − a , x ∈ ( a , b ) ) 0 e l s e f(x)=\left\{\begin{matrix}\frac{1}{b-a} ,&x\in(a,b)) \\ 0 &else \end{matrix}\right. f(x)={b−a1,0x∈(a,b))else | f ( x ) = 1 ( 2 π σ 2 ) 1 2 e x p { − 1 2 σ 2 ( x − μ ) 2 } f(x)=\frac{1}{(2\pi\sigma^2)^{\frac{1}{2}}}exp\{-\frac{1}{2\sigma^2}(x-\mu)^2\} f(x)=(2πσ2)211exp{−2σ21(x−μ)2} | f ( x ) = ∣ 2 π k ⃗ ∣ 1 2 e x p { − 1 2 ( x − m ⃗ ) T k ⃗ − 1 ( x − m ⃗ ) } f(x)=|2\pi\vec{k}|^\frac{1}{2}exp\{-\frac{1}{2}(x-\vec{m})^T\vec k^{-1}(x-\vec m)\} f(x)=∣2πk∣21exp{−21(x−m)Tk−1(x−m)}m:均值矢量 k ⃗ \vec k k协方差矢量 | |
| 微分熵 | h ( x ) = ∫ a b f ( x ) l o g f ( x ) d x = l o g ( b − a ) h(x)=\int_a^bf(x)logf(x)dx=log(b-a) h(x)=∫abf(x)logf(x)dx=log(b−a)当b-a<1时,h(x)<0 | h ( x ) = − l o g e ∫ − ∞ ∞ f ( x ) l n f ( x ) d x = 1 2 l o g ( 2 π e σ 2 ) h(x)=-loge\int_{-\infty}^{\infty}f(x)lnf(x)dx=\frac{1}{2}log(2\pi e\sigma^2) h(x)=−loge∫−∞∞f(x)lnf(x)dx=21log(2πeσ2) | h ( x ) = 1 2 l o g ∣ 2 π e k ⃗ ∣ h(x)=\frac{1}{2}log|2\pi e\vec k| h(x)=21log∣2πek∣ |
七、最大熵分布
-
条件一:(幅值约束)对于r有限长范围(a,b)使其最大熵的分布是均匀分布
u ( x ) = 1 b − a → u(x)=\frac{1}{b-a} \rightarrow u(x)=b−a1→、 0 ≤ D ( f ∣ ∣ x ) → h f ( x ) = l o g ( b − a ) 0 \le D(f||x) \rightarrow h_f(x)=log(b-a) 0≤D(f∣∣x)→hf(x)=log(b−a) -
条件二:(功率约束)给定协方差矩阵 k ⃗ \vec k k,零均值的多元高斯分布能使熵在 ( − ∞ , ∞ ) n (-\infty,\infty)^n (−∞,∞)n上最大
ϕ ( x ) = ∥ 2 π k ⃗ ∥ 1 2 e x p { − 1 2 x T k ⃗ − 1 x ⃗ } \phi (x)=\|2\pi\vec{k}\|^\frac{1}{2}exp\{-\frac{1}{2}x^T\vec k^{-1}\vec x\} ϕ(x)=∥2πk∥21exp{−21xTk−1x};
0 ≤ D ( f ∣ ∣ x ) = h f ( x ) − E f l o g ϕ ( x ) → h f ( x ) ≤ − ( l o g e ) E f ( − 1 2 l n ∣ 2 π k ⃗ ∣ − 1 2 x T k ⃗ − 1 x ) = h ϕ ( x ) 0 \le D(f||x)=h_f(x)-E_flog\phi(x) \rightarrow h_f(x)\le-(loge)E_f(-\frac{1}{2}ln|2\pi \vec k|-\frac{1}{2}x^T \vec k^{-1}x)=h_{\phi (x)} 0≤D(f∣∣x)=hf(x)−Eflogϕ(x)→hf(x)≤−(loge)Ef(−21ln∣2πk∣−21xTk−1x)=hϕ(x)
常需要的不等式公式
H ( Y ∣ X ) ≤ H ( X ) H(Y|X)\le H(X) H(Y∣X)≤H(X),X和Y互相独立时,等号成立
H ( X 1 , X 2 , . . . . X n ) ≤ ∑ i = 1 n H ( X i ) H(X_1,X_2,....X_n)\le \sum_{i=1}^nH(X_i) H(X1,X2,....Xn)≤∑i=1nH(Xi),当且仅当 X i X_i Xi互相独立时等号成立
参考文章:通信算法基础知识汇总(5)、通信算法基础知识汇总(8)
相关文章:

熵 | 无线通信知识
文章目录 一、信息论(熵、联合熵、条件熵)二、Bernoulli熵三、联合熵和条件熵四、互信息五、相对熵(KL距离)六、微分熵七、最大熵分布常需要的不等式公式 一、信息论(熵、联合熵、条件熵) 熵定义: H ( X ) E [ − l …...
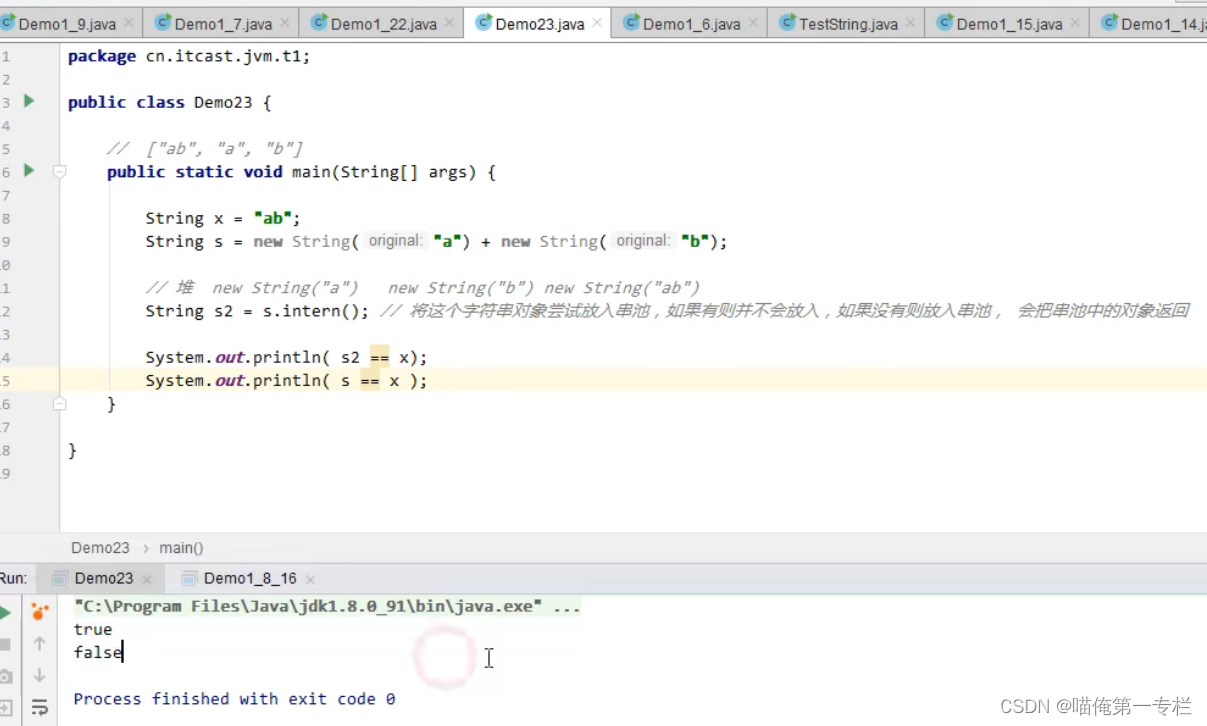
黑马JVM总结(七)
(1)StringTable_编译器优化 “a”“b”对应#4:是去常量池中找ab的这个符号 astore 5:是把这个存入编号为5的局部变量 “ab”对应的指令 #4,跟“a”“b”对应#4下面弄是一样的 在执行s3“ab”这行个代码时…...

Vue3核心语法一
Vue3核心语法一 rectiveshallowReactiverefcomputedwatchwatchEffet 使用Vue3创建项目template中标签可以多个根标签,可以通过setup开启组合式API,组合式API优点可以使相同业务放到一起 rective 定义响应式数据, import { reactive} from "vue";const data reactiv…...

5.11.Webrtc接口的设计原理
在上节课中呢,我向你介绍了web rtc的接口宏,那有很多同学会产生疑问啊,那觉得web rtc为什么要把接口设计的这么复杂?还非要通过宏来实现一个代理类,再通过代理类来调用到web rtc内部。 那为什么要这么设计呢…...

2022年09月 C/C++(八级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C++编程(1~8级)全部真题・点这里 第1题:道路 N个以 1 … N 标号的城市通过单向的道路相连:。每条道路包含两个参数:道路的长度和需要为该路付的通行费(以金币的数目来表示) Bob and Alice 过去住在城市 1.在注意到Alice在他们过去喜欢玩的纸牌游戏中作弊后,Bob和她分手…...
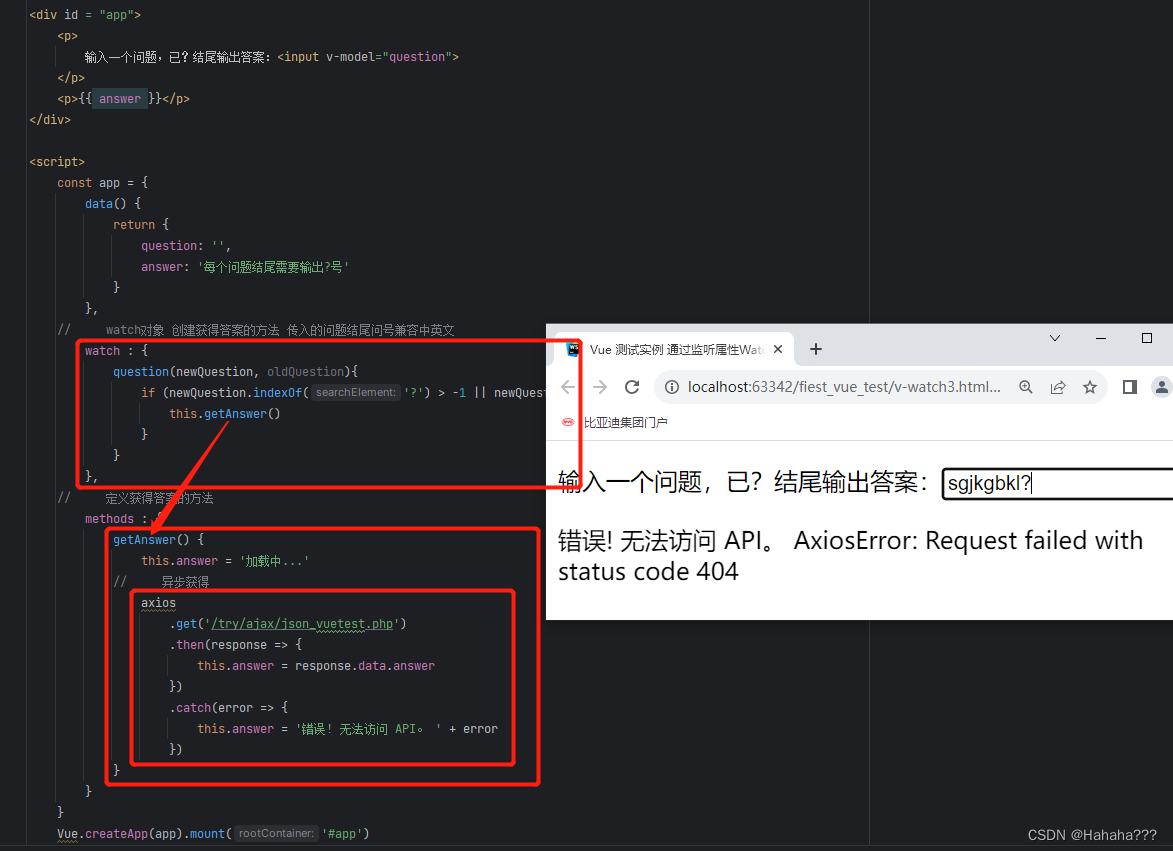
Vue3 监听属性-watch
文章目录 Vue3 监听属性-watch1. 概念2. 实例2.1 通过使用 watch 实现计数器2.2 千米与米之间的换算2.3 异步加载中使用 watch2.4 小计 Vue3 监听属性-watch 1. 概念 Vue3 监听属性 watch,可以通过 watch 来响应数据的变化。 watch 的作用:用于监测响应…...
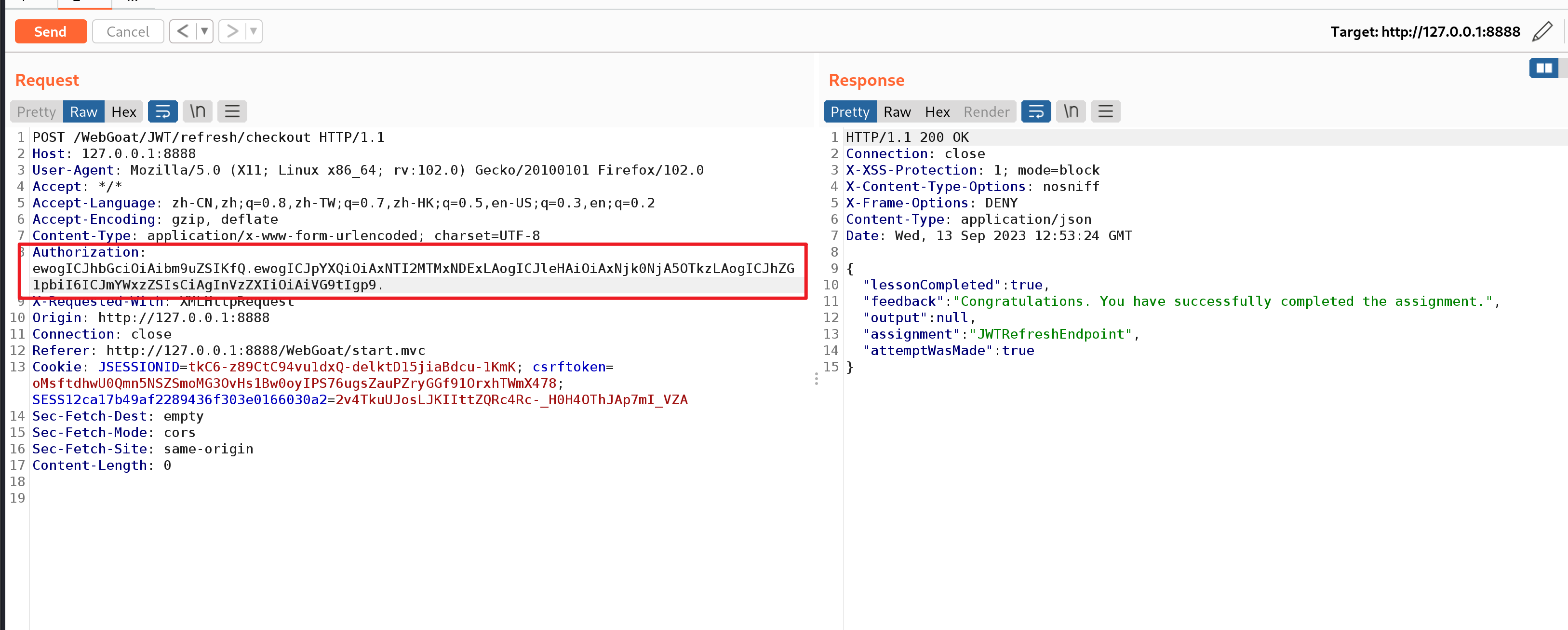
JWT安全
文章目录 理论知识cookie(放在浏览器)session(放在 服务器)tokenjwt(json web token)headerpayloadSignatureJWT通信流程 JWT与Token 区别相同点区别 WebGoat靶场--JWT tokens环境启动第四关第五关第七关 属于越权漏洞 理论知识 cookie(放在浏览器) …...
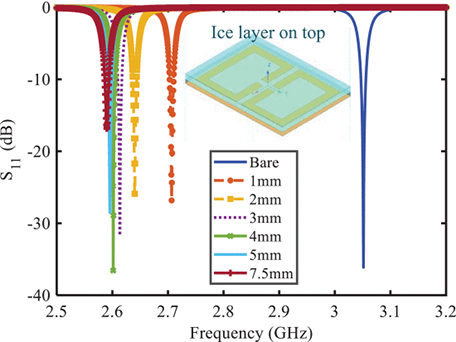
LabVIEW利用人工神经网络辅助进行结冰检测
LabVIEW利用人工神经网络辅助进行结冰检测 结冰对各个领域构成重大威胁,包括但不限于航空航天和风力涡轮机行业。在起飞过程中,飞机机翼上轻微积冰会导致升力降低25%。研究报告称,涡轮叶片上的冰堆积可在19个月的运行时间内造成29MWh的功率损…...

Linux安装MySQL8.0
又又又又..Linux装MySQL。 删除原有的MySQL 查看安装的mysql信息:rpm -qa|grep -i mysql 删除mysql相关服务:rpm -e --nodeps 查询mysql遗留文件和依赖信息:find / -name mysql 手动删除mysql配置文件:rm -rf /etc/my.cnf 相关…...
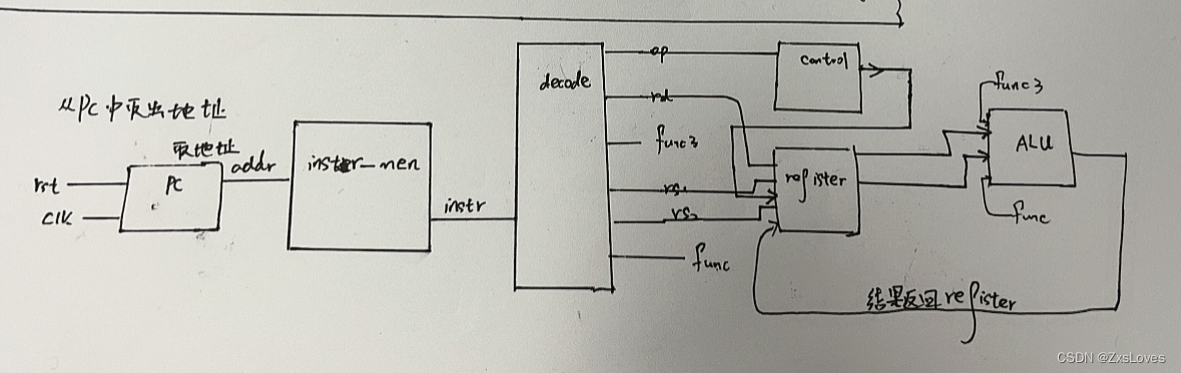
【【萌新编写RISCV之前言CPU的部分介绍.3】】
萌新编写RISCV之前言CPU的部分介绍.3 CPU的数字电路结构实际十分简单,最主要的模块有PC(地址生成),ALU(运算),Register(寄存),Decode(译码&#…...

dl_model_param
set_dl_model_param —设置深度学习模型的参数 get_dl_model_param — Return the parameters of a deep learning model 返回深度学习模型的参数 使用read_dl_model读取前一步初始化后的网络模型,得到模型的句柄DLModelHandle。 接着用read_dict读取预处理后的数…...
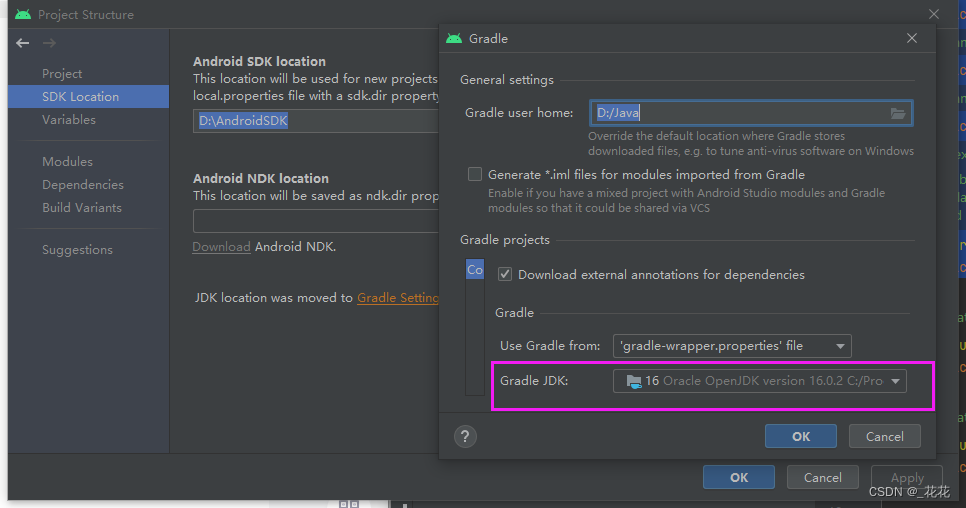
Android相机调用-CameraX【外接摄像头】【USB摄像头】
Android相机调用有原生的Camera和Camera2,我觉得调用代码都太复杂了,CameraX调用代码简洁很多。 说明文档:https://developer.android.com/jetpack/androidx/releases/camera?hlzh-cn 现有查到的调用资料都不够新,对于外接摄像…...

第一个Java程序
1. 将扩展名.text更改为.java 2.文件夹(Hello.java)上方输入“cmd空格回车”(没有加号) 3.在命令提示符内输入“javac空格文件夹名称.java回车” (javac空格Hello.java回车) 执行成功后,文件夹下多一个Hello.class…...

OpenCV之霍夫变换检测直线
霍夫变换 首先是笛卡尔坐标系到霍夫空间的转换,比如笛卡尔坐标系中有一条直线 yaxb。 笛卡尔坐标系中一条直线,对应霍夫空间的一个点。 反过来同样成立(霍夫空间的一条直线,对应笛卡尔坐标系的一个点) 原理其实很简单 …...
lv3 嵌入式开发-11 Linux下GDB调试工具
目录 1 GDB简介 2 GDB基本命令 3 GDB调试程序 1 GDB简介 GDB是GNU开源组织发布的一个强大的Linux下的程序调试工具。 一般来说,GDB主要帮助你完成下面四个方面的功能: 1、启动你的程序,可以按照你的自定义的要求随心所欲的运行程序&#…...
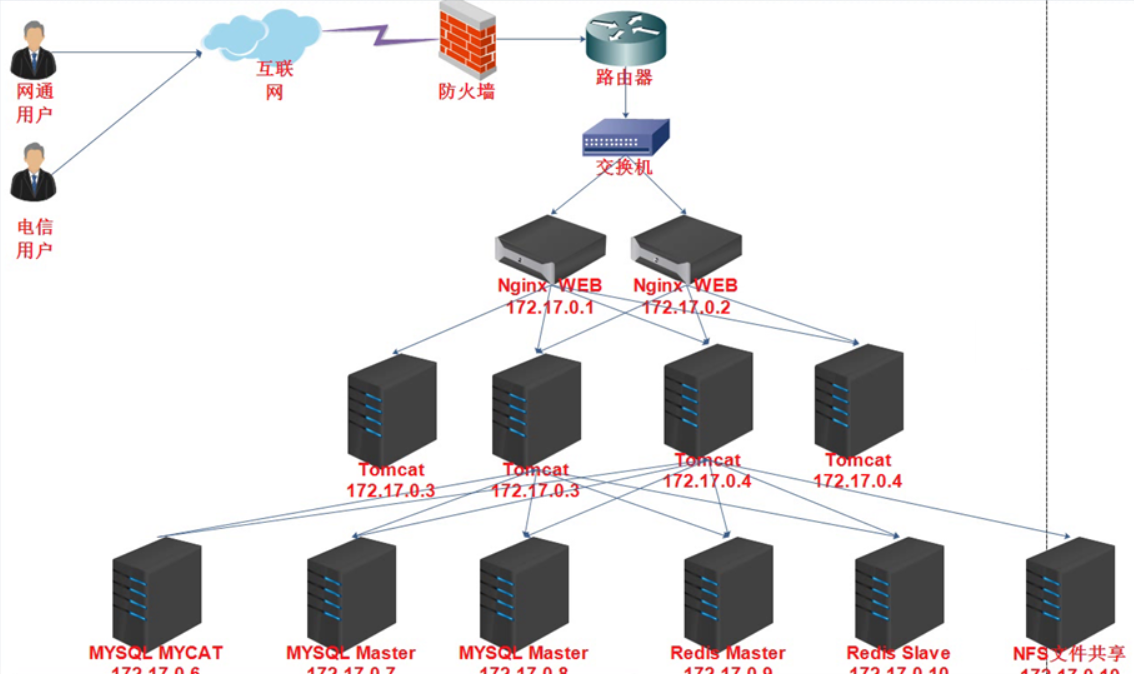
Zabbix监控平台概念
1.概念 Zabbix是一款开源的、免费的、分布式监控平台支持web管理,WEB界面可以方便管理员使用可以监控硬件服务器CPU温度、风扇转速、操作系统CPU、EME、DISK、I/O、流量宽带、负载、端口、进程等Zabbix是C/S架构,Client客户端和Server端组成 2.Zabbix可…...
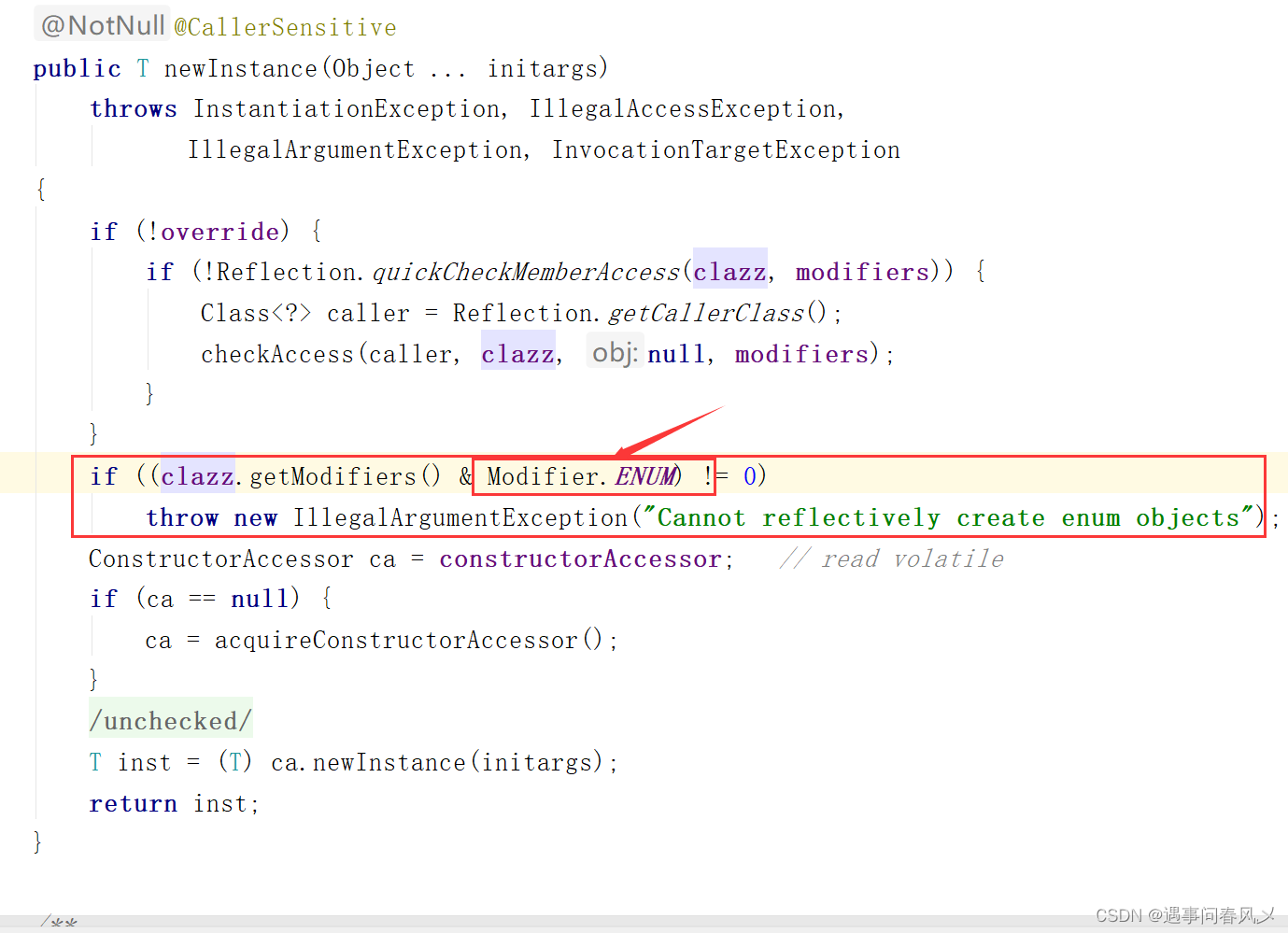
【javaSE】 枚举与枚举的使用
文章目录 🎄枚举的背景及定义⚾枚举特性总结: 🌲枚举的使用🚩switch语句🚩常用方法📌示例一📌示例二 🎍枚举优点缺点🌴枚举和反射🚩枚举是否可以通过反射&…...
NetSuite知识会汇编-管理员篇顾问篇2023
本月初,开学之际,我们发布了《NetSuite知识会汇编-用户篇 2023》,这次发布《NetSuite知识会汇编-管理员篇&顾问篇2023》。本篇挑选了近两年NetSuite知识会中的一些文章,涉及开发、权限、系统管理等较深的内容,共19…...

根号分治与多项式的巧妙结合:GYM-104386G
使用范围:序列上对于每种数的计数问题 考虑对每种数的出现次数进行根号分治 如果出现次数很少,直接平方暴力即可 如果很大考虑任意 ( i , j ) (i,j) (i,j),我们拆一下,再移一下,然后就变成了卷积形式...

通过FTP高速下载几百G数据
基因组下载 (FTP) 常见问题解答 基因组FTP站点有哪些亮点?下载多个基因组组装数据的最简单方法是什么?下载大型数据集的最佳协议是什么?为什么 NCBI 基因组 FTP 站点要重组?我如何及时了解 NCBI 基因组 FTP 站点的变化?...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
