想要精通算法和SQL的成长之路 - 受限条件下可到达节点的数目
想要精通算法和SQL的成长之路 - 受限条件下可到达节点的数目
- 前言
- 一. 相交链表(邻接图和DFS)
前言
想要精通算法和SQL的成长之路 - 系列导航
一. 相交链表(邻接图和DFS)
原题链接
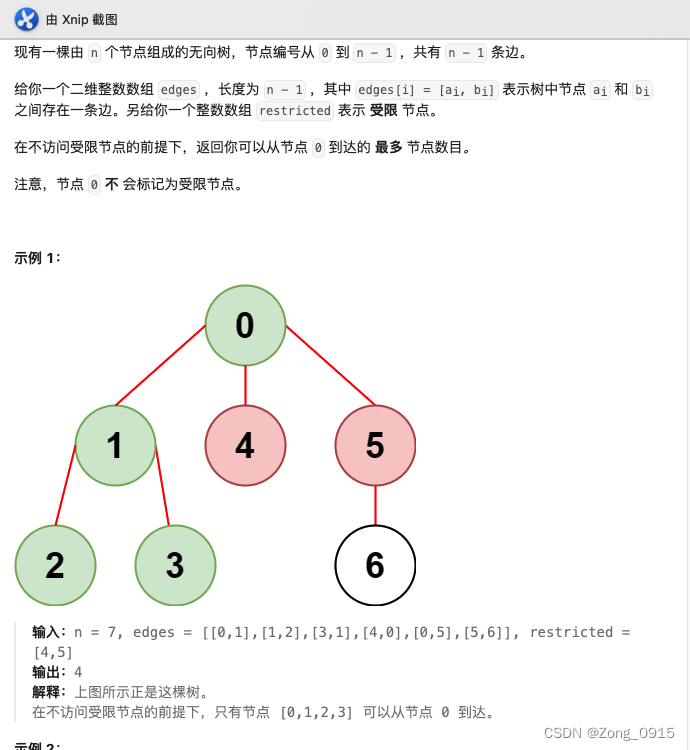
public int reachableNodes(int n, int[][] edges, int[] restricted) {
}
我们读一下题目,我们总结几个核心的点:
- 无向图。
- 受限节点。
- 题目用一个二维数组代表图。
针对第一个点和第三个点:我们用何种方式通过二维数组来构建出一个无向图?
使用邻接图。在Java当中,邻接图可以用下面一个模板来完成:
List<Integer>[] adj = new List[n];
// 初始化每个数组
for (int i = 0; i < n; i++) {adj[i] = new ArrayList<>();
}
for (int[] edge : edges) {adj[前继节点].add(后继节点);
}
那么由于本题目又特意声明了它是一个无向图,我们前后顺序换一下再存储一次即可:
adj[前继节点].add(后继节点);
adj[后继节点].add(前继节点);
针对第二点:受限节点。我们用一个一维数组,代表每个元素是否受限,下标即是对应的元素值:
boolean[] limits = new boolean[n];
for (int i : restricted) {limits[i] = true;
}
有了这些数据,我们就可以通过DFS去递归遍历这颗树:
- 我们指定对应的元素 0 作为根节点,向后继节点递归。
- 同时因为无向的关系,我们在递归节点的时候,需要做判断,当前节点并不是父节点,满足条件才可往深层递归。否则就会出现死循环。
例如:以上图的案例,最终的无向图数据部分如下:
- 0–>1,4,5。
- 1->0,1,3
死循环逻辑如下:
- 第一层:倘若当前节点为1的时候,根据顺序深层递归。递归节点0。
- 第二层:当前遍历节点为0,发现0的相邻节点有1,开始递归节点1。回到第一步。
- 第三层…
因此我们在dfs递归的时候需要有两个参数:
- 当前节点。
- 当前节点的父节点。
同时我们用一个全局变量count代表递归的数量(即是题目返回要求)
void dfs(int root, int pre) {count++;for (int node : adj[root]) {if (!limits[node] && node != pre) {dfs(node, root);}}
}
最终完整代码如下:
public class Test2368 {int count = 0;List<Integer>[] adj;boolean[] limits;public int reachableNodes(int n, int[][] edges, int[] restricted) {// 邻接图数据构建adj = new List[n];for (int i = 0; i < n; i++) {adj[i] = new ArrayList<>();}for (int[] edge : edges) {adj[edge[0]].add(edge[1]);adj[edge[1]].add(edge[0]);}// 构建受限节点数组limits = new boolean[n];for (int i : restricted) {limits[i] = true;}// 开始递归,从根节点0开始,父节点不存在,我们传一个-1dfs(0, -1);return count;}void dfs(int root, int pre) {count++;// adj[root] 就是与 当前节点 所有的相邻节点for (int node : adj[root]) {// 非受限节点并且当前节点并不是父节点的时候,继续往下递归if (!limits[node] && node != pre) {dfs(node, root);}}}
}
相关文章:

想要精通算法和SQL的成长之路 - 受限条件下可到达节点的数目
想要精通算法和SQL的成长之路 - 受限条件下可到达节点的数目 前言一. 相交链表(邻接图和DFS) 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 相交链表(邻接图和DFS) 原题链接 public int reachableNodes(int n, int[][] ed…...
加快项目开发进度常用5种方法
项目进度管理是根据进度目标,制定合理的进度计划,全程监控项目进度的执行情况。这样有利于明确项目目标,协调团队行动,提高开发效率,从而最大化项目利益。而加快项目进度,有利于提高项目整体效率࿰…...

leetcode做题笔记136. 只出现一次的数字
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。 你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。 思路一:快排(…...

vuex 模拟异步调用
在页面中首先定义一个调用vuex异步函数的方法 <el-button click fetchData></el-button> {{asyncData}} vuex 中 const store new Vuex.Store({state: {asyncData: null,},mutations: {SET_ASYNC_DATA(state, data) {state.asyncData data;},},actions: {fe…...

error:Failed building wheel for XXX
解决方案适用于大多数的pip 安装时出现的Failed building wheel for XXX 出现问题 按以往快速安装包的经验,第一反应当然是使用简单又快捷的terminal命令加上镜像,如下: pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple结…...

【linux命令讲解大全】112.Linux 系统管理工具:dpkg-statoverride 和 dstat 的使用介绍
文章目录 dpkg-statoverride补充说明语法选项实例 dstat补充说明下载安装方法一方法二 使用说明语法常用选项实例 从零学 python dpkg-statoverride 在 Debian Linux 中覆盖文件的所有权和模式。 补充说明 dpkg-statoverride 命令用于在 Debian Linux 中覆盖文件的所有权和模…...

ffmpeg草稿
avformat 用于解析容器和协议(protocol)。 avcodec 用于编码和解码基本流(您已经拥有的)。 Qt/C音视频开发44-本地摄像头推流(支持分辨率/帧率等设置/实时性极高)_feiyangqingyun的博客-CSDN博客 void FFmpegThread::initInputFormat() {//本地摄像头/桌…...

熵 | 无线通信知识
文章目录 一、信息论(熵、联合熵、条件熵)二、Bernoulli熵三、联合熵和条件熵四、互信息五、相对熵(KL距离)六、微分熵七、最大熵分布常需要的不等式公式 一、信息论(熵、联合熵、条件熵) 熵定义: H ( X ) E [ − l …...
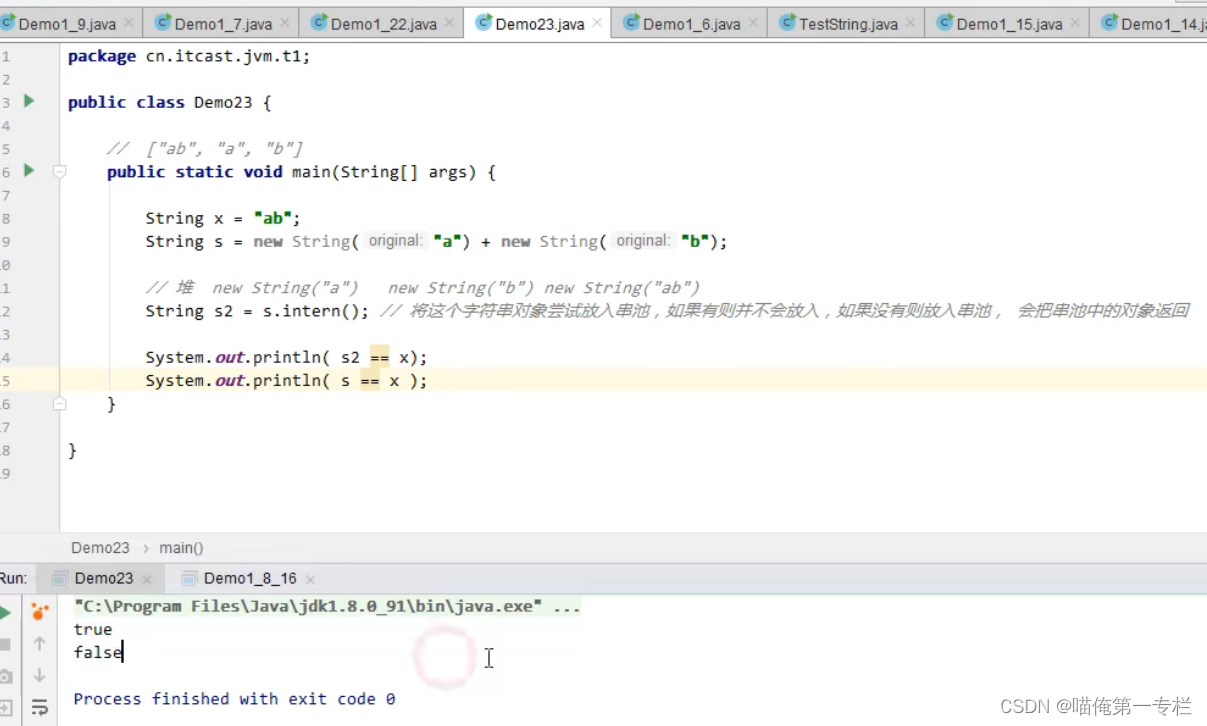
黑马JVM总结(七)
(1)StringTable_编译器优化 “a”“b”对应#4:是去常量池中找ab的这个符号 astore 5:是把这个存入编号为5的局部变量 “ab”对应的指令 #4,跟“a”“b”对应#4下面弄是一样的 在执行s3“ab”这行个代码时…...

Vue3核心语法一
Vue3核心语法一 rectiveshallowReactiverefcomputedwatchwatchEffet 使用Vue3创建项目template中标签可以多个根标签,可以通过setup开启组合式API,组合式API优点可以使相同业务放到一起 rective 定义响应式数据, import { reactive} from "vue";const data reactiv…...

5.11.Webrtc接口的设计原理
在上节课中呢,我向你介绍了web rtc的接口宏,那有很多同学会产生疑问啊,那觉得web rtc为什么要把接口设计的这么复杂?还非要通过宏来实现一个代理类,再通过代理类来调用到web rtc内部。 那为什么要这么设计呢…...

2022年09月 C/C++(八级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C++编程(1~8级)全部真题・点这里 第1题:道路 N个以 1 … N 标号的城市通过单向的道路相连:。每条道路包含两个参数:道路的长度和需要为该路付的通行费(以金币的数目来表示) Bob and Alice 过去住在城市 1.在注意到Alice在他们过去喜欢玩的纸牌游戏中作弊后,Bob和她分手…...
Vue3 监听属性-watch
文章目录 Vue3 监听属性-watch1. 概念2. 实例2.1 通过使用 watch 实现计数器2.2 千米与米之间的换算2.3 异步加载中使用 watch2.4 小计 Vue3 监听属性-watch 1. 概念 Vue3 监听属性 watch,可以通过 watch 来响应数据的变化。 watch 的作用:用于监测响应…...
JWT安全
文章目录 理论知识cookie(放在浏览器)session(放在 服务器)tokenjwt(json web token)headerpayloadSignatureJWT通信流程 JWT与Token 区别相同点区别 WebGoat靶场--JWT tokens环境启动第四关第五关第七关 属于越权漏洞 理论知识 cookie(放在浏览器) …...
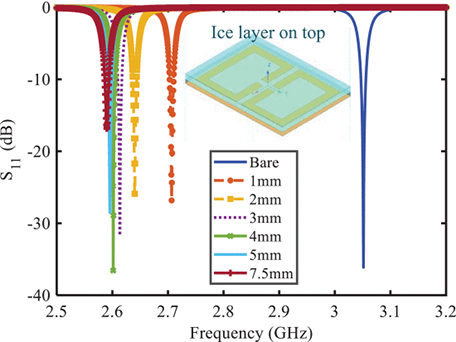
LabVIEW利用人工神经网络辅助进行结冰检测
LabVIEW利用人工神经网络辅助进行结冰检测 结冰对各个领域构成重大威胁,包括但不限于航空航天和风力涡轮机行业。在起飞过程中,飞机机翼上轻微积冰会导致升力降低25%。研究报告称,涡轮叶片上的冰堆积可在19个月的运行时间内造成29MWh的功率损…...

Linux安装MySQL8.0
又又又又..Linux装MySQL。 删除原有的MySQL 查看安装的mysql信息:rpm -qa|grep -i mysql 删除mysql相关服务:rpm -e --nodeps 查询mysql遗留文件和依赖信息:find / -name mysql 手动删除mysql配置文件:rm -rf /etc/my.cnf 相关…...
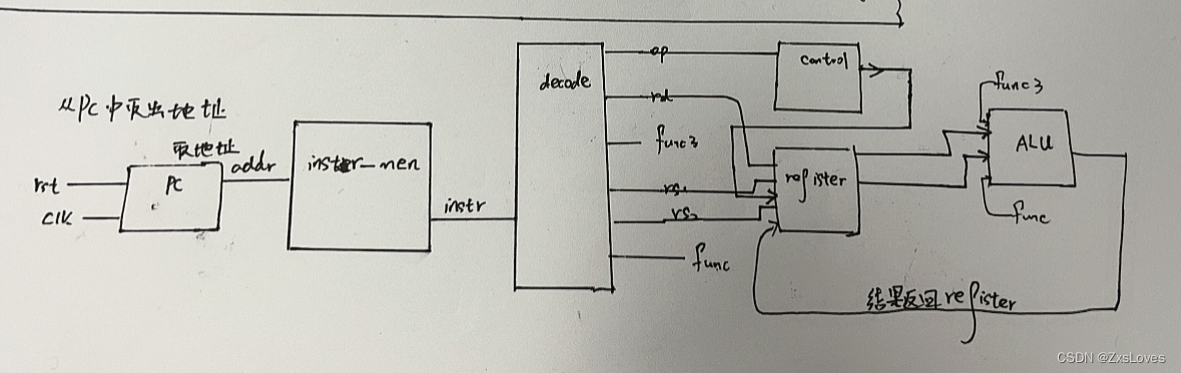
【【萌新编写RISCV之前言CPU的部分介绍.3】】
萌新编写RISCV之前言CPU的部分介绍.3 CPU的数字电路结构实际十分简单,最主要的模块有PC(地址生成),ALU(运算),Register(寄存),Decode(译码&#…...

dl_model_param
set_dl_model_param —设置深度学习模型的参数 get_dl_model_param — Return the parameters of a deep learning model 返回深度学习模型的参数 使用read_dl_model读取前一步初始化后的网络模型,得到模型的句柄DLModelHandle。 接着用read_dict读取预处理后的数…...
Android相机调用-CameraX【外接摄像头】【USB摄像头】
Android相机调用有原生的Camera和Camera2,我觉得调用代码都太复杂了,CameraX调用代码简洁很多。 说明文档:https://developer.android.com/jetpack/androidx/releases/camera?hlzh-cn 现有查到的调用资料都不够新,对于外接摄像…...

第一个Java程序
1. 将扩展名.text更改为.java 2.文件夹(Hello.java)上方输入“cmd空格回车”(没有加号) 3.在命令提示符内输入“javac空格文件夹名称.java回车” (javac空格Hello.java回车) 执行成功后,文件夹下多一个Hello.class…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
