markdown学习笔记
1.文字(依靠HTML)
1.1文字缩进-空格转义符
单字符空:  半字符空: 
1.2文字对齐
「居中:」<center> 居中 </center> or <p align="center"> 居中 </p>
「左对齐:」<p align="left">左对齐</p>
「右对齐:」<p align="right">右对齐</p>
「居中:」
居中 or居中
「左对齐:」左对齐
「右对齐:」右对齐
1.3 字体与颜色(font=字体)
1.3.1 字体-face
<font face="宋体">字体</font>,
<font face="黑体">字体</font>,
<font face="微软雅黑">字体</font>,
<font face="微软正黑体">字体</font>,
<font face="仿宋">字体</font>,
<font face="楷体">字体</font>,
<font face="仿宋">字体</font>
字体,字体,字体,字体,字体,字体,字体
1.3.2 大小更换-size
Size规定文本的尺寸大小,取值从 1 到 7,浏览器默认值是 3。
<font face="黑体" size=5>我是黑体5号字</font>
我是黑体2号字
1.3.3 颜色-color
<font color=red size=3>红色</font>
红色
1.3.4下划线-u
<u>是非真假无法判断,不如坚强。</u>
是非真假无法判断,不如坚强。
2.表格
2.1 语法格式
| 表头 | 表头 |
| ---- | ---- |
| 单元格 | 单元格 |
| 单元格 | 单元格 |
| 表头 | 表头 |
|---|---|
| 单元格 | 单元格 |
| 单元格 | 单元格 |
2.2 表格对齐
-: 设置内容和标题栏居右对齐。
:- 设置内容和标题栏居左对齐。
:-: 设置内容和标题栏居中对齐。
实例如下:
| 左对齐 | 右对齐 | 居中对齐 |
| :-----| ----: | :----: |
| 单元格 | 单元格 | 单元格 |
| 单元格 | 单元格 | 单元格 |
实例如下:
| 左对齐 | 右对齐 | 居中对齐 |
|---|---|---|
| 傲来雾花果香 | 定海一棒万妖朝 | 东海外水帘中,齐天比高仙折腰 |
| 素衣着泪情诗 | 待你未归人潮逝 | 初相识唇上血,千古第一为红颜 |
3.背景色-如表
<table><tbody><tr><th>颜色名</th><th>十六进制颜色值</th><th>颜色</th></tr><tr><td><font color="AliceBlue">AliceBlue</font></td><td><font color="AliceBlue">F0F8FF</font></td><td bgcolor="AliceBlue">rgb(240, 248, 255)</td></tr><tr><td><font color="AntiqueWhite">AntiqueWhite</font></td><td><font color="AntiqueWhite">#FAEBD7</font></td><td bgcolor="AntiqueWhite">rgb(250, 235, 215)</td></tr><tr><td><font color="Lavender">Lavender</font></td><td><font color="Lavender">#E6E6FA</font></td><td bgcolor="Lavender">rgb(230, 230, 250)</td></tr><tr><td><font color="LavenderBlush">LavenderBlush</font></td><td><font color="LavenderBlush">#FFF0F5</font></td><td bgcolor="LavenderBlush">rgb(255, 240, 245)</td></tr><tr><td><font color=" LightPink"> LightPink</font></td><td><font color=" LightPink">#FFB6C1</font></td><td bgcolor=" LightPink">rgb(255, 182, 193)</td></tr><tr><td><font color="LightSalmon">LightSalmon</font></td><td><font color="LightSalmon">#FFA07A</font></td><td bgcolor="LightSalmon">rgb(255, 160, 122)</td></tr><tr><td><font color="MintCream">MintCream</font></td><td><font color="MintCream">#F5FFFA</font></td><td bgcolor="MintCream">rgb(245, 255, 250)</td></tr><tr><td><font color="MistyRose">MistyRose</font></td><td><font color="MistyRose">#FFE4E1</font></td><td bgcolor="MistyRose">rgb(255, 228, 225)</td></tr><tr><td><font color="Moccasin">Moccasin</font></td><td><font color="Moccasin">#FFE4B5</font></td><td bgcolor="Moccasin">rgb(255, 228, 181)</td></tr><tr><td><font color="MintCream">MintCream</font></td><td><font color="MintCream">#F5FFFA</font></td><td bgcolor="MintCream">rgb(245, 255, 250)</td></tr><tr><td><font color="PaleVioletRed">PaleVioletRed</font></td><td><font color="PaleVioletRed">#D87093</font></td><td bgcolor="PaleVioletRed">rgb(216, 112, 147)</td></tr>
</table>
| 颜色名 | 十六进制颜色值 | 颜色 |
|---|---|---|
| AliceBlue | F0F8FF | rgb(240, 248, 255) |
| AntiqueWhite | #FAEBD7 | rgb(250, 235, 215) |
| Lavender | #E6E6FA | rgb(230, 230, 250) |
| LavenderBlush | #FFF0F5 | rgb(255, 240, 245) |
| LightPink | #FFB6C1 | rgb(255, 182, 193) |
| LightSalmon | #FFA07A | rgb(255, 160, 122) |
| MintCream | #F5FFFA | rgb(245, 255, 250) |
| MistyRose | #FFE4E1 | rgb(255, 228, 225) |
| Moccasin | #FFE4B5 | rgb(255, 228, 181) |
| MintCream | #F5FFFA | rgb(245, 255, 250) |
| PaleVioletRed | #D87093 | rgb(216, 112, 147) |
4.图片
4.1图片大小(依靠HTML)
1.使用zoom
<img src="https://img-blog.csdnimg.cn/img_convert/ef9b0688c1fed69d94b2fd719f1693d3.png" alt="13221564654" style="zoom: 33%;" />
<img src="https://img-blog.csdnimg.cn/img_convert/ef9b0688c1fed69d94b2fd719f1693d3.png" style="zoom: 25%;" />


2.设置style中的width

4.2多张图片并排显示
1.图片连接连着,不空格,不换行



2.居中图片
<center><img src="https://img-blog.csdnimg.cn/img_convert/ef9b0688c1fed69d94b2fd719f1693d3.png" width="100px" /></center>

5.图表
1.顺序图
2.流程图
流程图2
3.饼图
6.数学
1.数学公式
单边大括号: 程序 = { 数据结构 算法 程序=\left\{ \begin{matrix} 数据结构 \\ 算法 \end{matrix} \right. 程序={数据结构算法
程序=\left\{ \begin{matrix} 数据结构 \\ 算法 \end{matrix} \right.
分号:\frac {分子} {分母}
求和符号 y = β 0 + β 1 x + ∑ i = 1 k w i ( x − a i ) + y=\beta_0 +\beta_1 x+\sum_{i=1}^{k}{w_i(x-a_i)_+} y=β0+β1x+i=1∑kwi(x−ai)+
矩阵使用Markdown写矩阵_韩湘的博客-CSDN博客_markdown写矩阵
∏ \prod ∏
相关文章:

markdown学习笔记
markdown学习笔记 1.文字(依靠HTML) 1.1文字缩进-空格转义符 单字符空:  半字符空: 1.2文字对齐 「居中:」<center> 居中 </center> or <p align"center"> 居中 …...

C++项目实战——基于多设计模式下的同步异步日志系统-⑧-日志落地类设计
文章目录 专栏导读抽象基类StdoutSink类设计FileSink类设计RollBySizeSink类设计日志落地工厂类设计日志落地类整理日志落地拓展测试RollByTimeSink类设计测试代码测试完整代码 专栏导读 🌸作者简介:花想云 ,在读本科生一枚,C/C领…...
从零开始探索C语言(八)----指针
文章目录 1. 什么是指针?2. 如何使用指针?3. NULL 指针4. 指针的算术运算5. 指针数组6. 指向指针的指针7. 传递指针给函数8. 从函数返回指针 有人说,指针是C语言的灵魂,所以学习C语言,学习指针是很有必要的。 通过指针…...

SpringMVC 的三种异常处理方式详解
目录 1. 什么是异常 2. 为什么要全局异常处理 3. SpringMVC异常分类 4. 异常处理思路 5. 三种异常处理方式示例 ① 配置 SimpleMappingExceptionResolver 处理器 ② 实现 HandlerExceptionResolver 接口 ③ 使用ControllerAdviceExceptionHandler实现全局异常 6. 响应…...

莫比乌斯召回系统介绍
当前召回系统只能召回相关性高的广告,但不能保证该广告变现能力强。莫比乌斯做了如下两点创新: 在召回阶段,引入CPM等业务指标作为召回依据在召回阶段,引入CTR模型,从而召回更多相关性高且变现能力强的广告 参考 百度…...

使用ASM修改组件化 ARouter
工程目录图 1. apt生成的字节码文件 2. asm 生成的代码 请点击下面工程名称,跳转到代码的仓库页面,将工程 下载下来 Demo Code 里有详细的注释 代码:TestCompont...
第21章_瑞萨MCU零基础入门系列教程之事件链接控制器ELC
本教程基于韦东山百问网出的 DShanMCU-RA6M5开发板 进行编写,需要的同学可以在这里获取: https://item.taobao.com/item.htm?id728461040949 配套资料获取:https://renesas-docs.100ask.net 瑞萨MCU零基础入门系列教程汇总: ht…...

(二十八)大数据实战——Flume数据采集之kafka数据生产与消费集成案例
前言 本节内容我们主要介绍一下flume数据采集和kafka消息中间键的整合。通过flume监听nc端口的数据,将数据发送到kafka消息的first主题中,然后在通过flume消费kafka中的主题消息,将消费到的消息打印到控制台上。集成使用flume作为kafka的生产…...
vue3:22、vue-router的使用
import { createRouter, createWebHistory } from vue-router//history模式:createWebHistory //hash模式:createWebHashHistory//vite中的环境变量 import.meta.env.BASE_URL 就是vite.config.js中的base配置项 const router createRouter({history:…...

深入理解JVM虚拟机第五篇:一些常用的JVM虚拟机(二)
文章目录 一:JRockit VM的介绍 二:J9 VM的介绍 三:KVM和CDC/CLDC Hotspot 四:Azul VM的介绍 五:Liquid VM的介绍 六:Apache Harmoney 七:Microsoft JVM 八:Taobao JVM 九&a…...

导数公式及求导法则
目录 基本初等函数的导数公式 求导法则 有理运算法则 复合函数求导法 隐函数求导法 反函数求导法 参数方程求导法 对数求导法 基本初等函数的导数公式 基本初等函数的导数公式包括: C0(x^n)nx^(n-1)(a^x)a^x*lna(e^x)e^x(loga(x))1/(xlna)(lnx)1/x(sinx)cos…...
SpringMVC系列(六)之JSON数据返回以及异常处理机制
目录 前言 一. JSON概述 二. JSON数据返回 1. 导入pom依赖 2. 添加配置文件(spring-mvc.xml) 3. ResponseBody注解使用 4. 效果展示 5. Jackson介绍 三. 全局异常处理 1. 为什么要全局异常处理 2. 异常处理思路 3. 异常处理方式一 4. 异常处…...
开展汽车消费者焦点小组座谈会调查)
民安智库(北京第三方窗口测评)开展汽车消费者焦点小组座谈会调查
民安智库近日开展了一场汽车消费者焦点小组座谈会,旨在深入了解目标消费者对汽车功能的需求和消费习惯,为汽车企业提供有针对性的解决方案。 在焦点小组座谈会中,民安智库公司(第三方市容环境指数测评)邀请了一群具有…...

【CVPR2021】MVDNet论文阅读分析与总结
Challenge: 现有的目标检测器主要融合激光雷达和相机,通常提供丰富和冗余的视觉信息 利用最先进的成像雷达,其分辨率比RadarNet和LiRaNet中使用的分辨率要细得多,提出了一种有效的深度后期融合方法来结合雷达和激光雷达信号。 MV…...
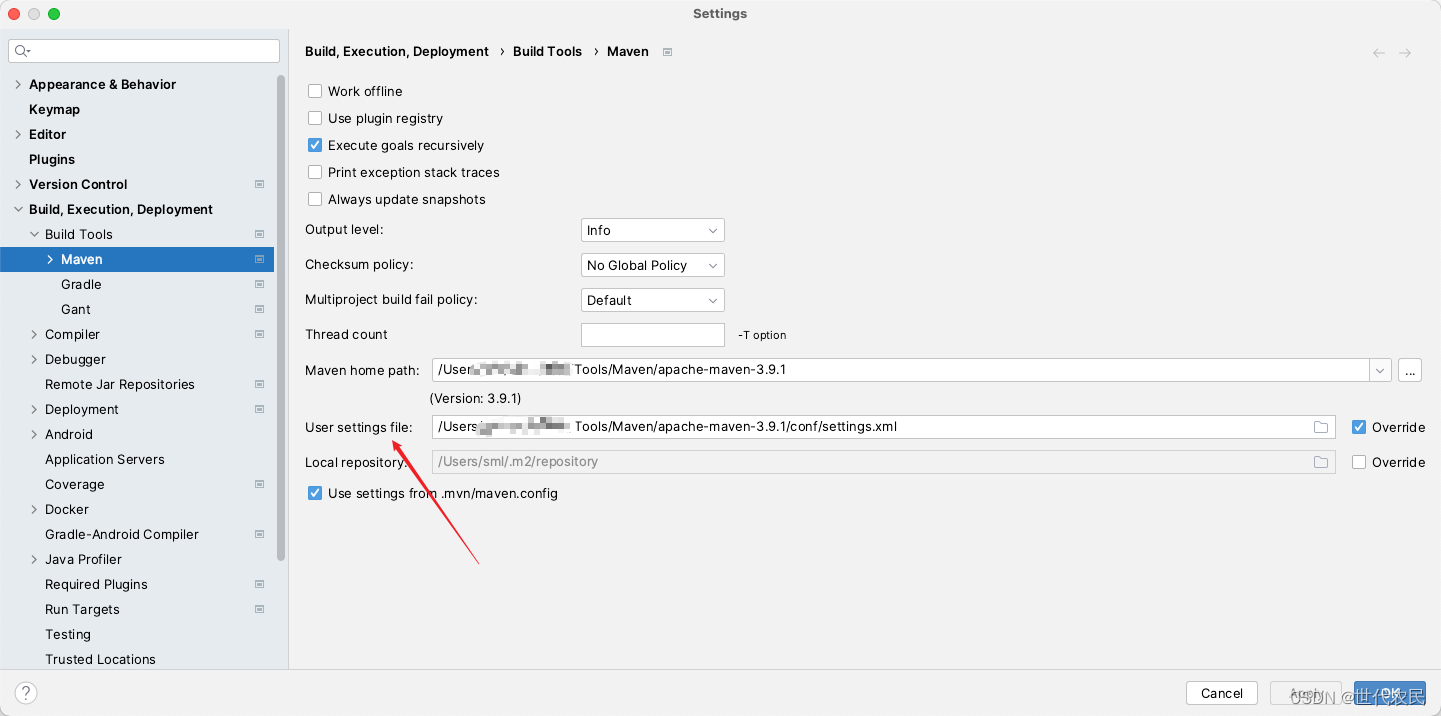
IDEA指定Maven settings file文件未生效
背景:在自己电脑上配置的时候,由于公司项目和我自己的项目的Maven仓库不一致,我就在项目中指定了各自的Maven配置文件。但是我发现公司的项目私有仓库地址IDEA总是识别不到! 俩个配置文件分别是: /Users/sml/Mine/研发…...

swift UI 和UIKIT 如何配合使用
SwiftUI和UIKit可以在同一个iOS应用程序中配合使用。它们是两个不同的用户界面框架,各自有自己的优势和特点。在现实开发中,很多iOS应用程序并不是一开始就完全采用SwiftUI或UIKit,而是根据需要逐步引入SwiftUI或者使用两者共存。 SwiftUI的…...

c语言练习题55:IP 地址⽆效化
IP 地址⽆效化 题⽬描述: 给你⼀个有效的 IPv4 地址 address ,返回这个 IP 地址的⽆效化版本。 所谓⽆效化 IP 地址,其实就是⽤ "[.]" 代替了每个 "."。 • ⽰例 1: 输⼊:address "1.1.1.…...

nvidia-persistenced 常驻
本文地址:blog.lucien.ink/archives/542 发现每次执行 nvidia-smi 都特别慢,发现是需要 nvidia-persistenced 常驻才可以,这个并不会在安装完驱动之后自动配置,需要手动设置一个自启。 cat <<EOF >> /etc/systemd/sy…...
)
leetcode 42, 58, 14(*)
42. Trapping Rain Water 1.暴力解法(未通过) class Solution { public:int trap(vector<int>& height) {int n height.size();int res 0;for(int i0; i<n; i){int r_max 0, l_max 0;for(int j i; j<n; j)r_max max(r_max, heigh…...

SpringCloud-微服务CAP原则
接上文 SpringCloud-Config配置中心 到此部分即微服务的入门。 总的来说,数据存放的节点数越多,分区容忍性就越高,但要复制更新的次数就越多,一致性就越难保证。同时为了保证一致性,更新所有节点数据所需要的时间就…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
