当前位置： 首页 > news >正文

pc端测试手机浏览器运行情况，主要是测试硬件功能

news 2026/2/8 11:10:37

测试h5震动摇晃等功能时不方便测试，需要连电脑显示调试数据

方法：
1.需要手机下载谷歌浏览器，pc端用edge或这谷歌浏览器
2.手机打开USB调试，打开要测试的网页
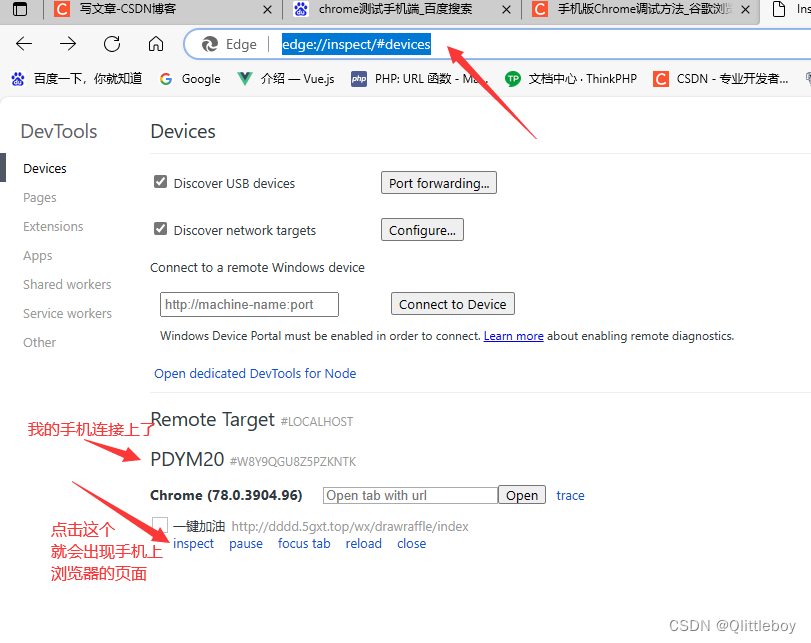
3.pc端地址栏输入edge://inspect/#devices（这里用的edge浏览器），回车
4.在这里插入图片描述
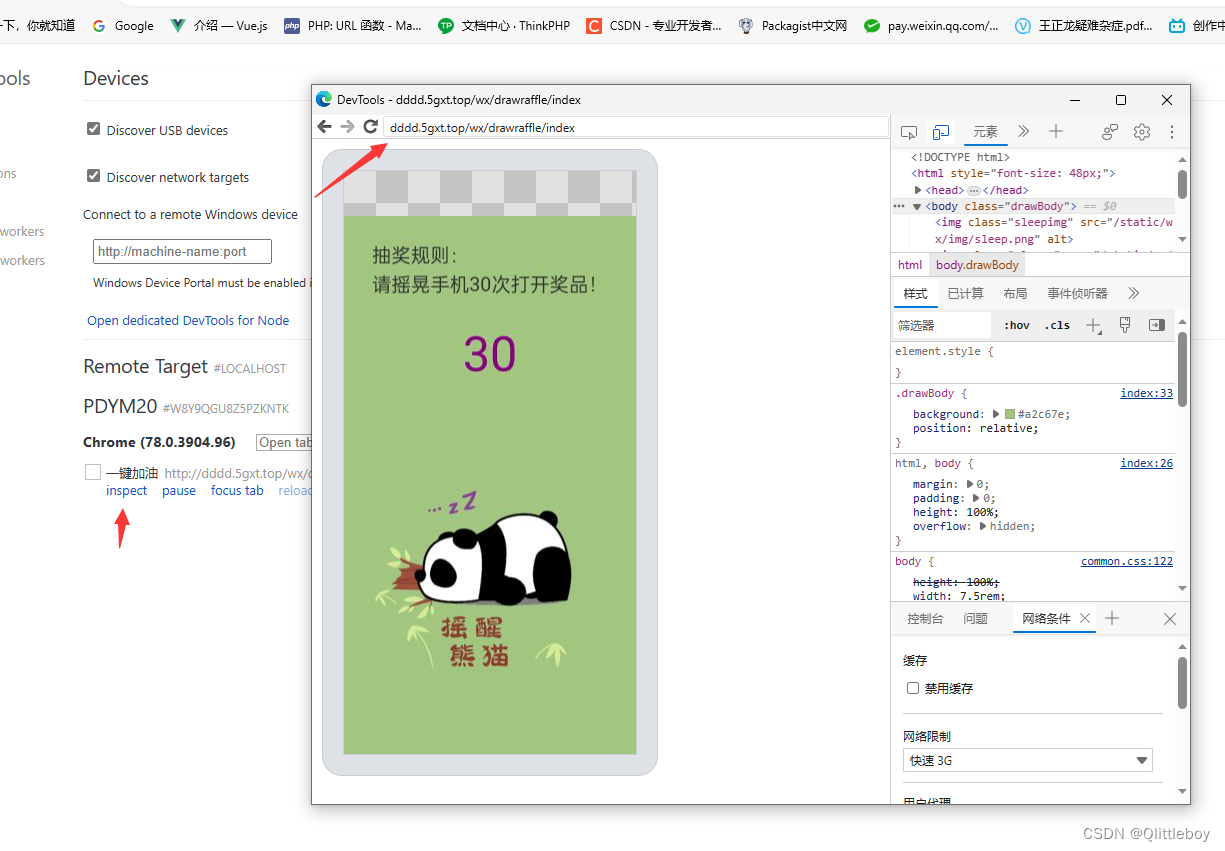
5.在这里插入图片描述

相关文章：

pc端测试手机浏览器运行情况，主要是测试硬件功能

测试h5震动摇晃等功能时不方便测试，需要连电脑显示调试数据 方法： 1.需要手机下载谷歌浏览器，pc端用edge或这谷歌浏览器 2.手机打开USB调试，打开要测试的网页 3.pc端地址栏输入edge://inspect/#devices（这里用的edge浏…...

编程日记 2023/9/14 13:54:09

软件概要设计-架构真题（二十五）

软件概要设计包括软件设计的结构、确定系统功能模块及其相互关系，主要采用（）描述程序的结构。（2018年） 程序流程图、PAD图和伪代码模块结构图、数据流图和盒图模块结构图、层次图和HIPO图程序流程图、数据流图和层次图…...

编程日记 2023/9/14 13:53:08

CSDN发文表情包整理

文章目录 简介部分Emoji表情符号简表人物自然物品地点符号 各种Emoji表情链接 简介 CSDN支持Markdown语法及Emoji表情，使用各种Emoji表情可以使得自己的博文更加生动多彩。一般有两种在支持Markdown的语法环境中添加Emoji表情：1.直接将表情包复制到文档…...

编程日记 2023/9/14 13:52:08

springBoot对接Apache POI 实现excel下载和上传

搭建springboot项目 此处可以参考 搭建最简单的SpringBoot项目_Steven-Russell的博客-CSDN博客 配置Apache POI 依赖 <dependency><groupId>org.apache.poi</groupId><artifactId>poi</artifactId><version>5.2.2</version> </…...

编程日记 2023/9/14 13:46:02

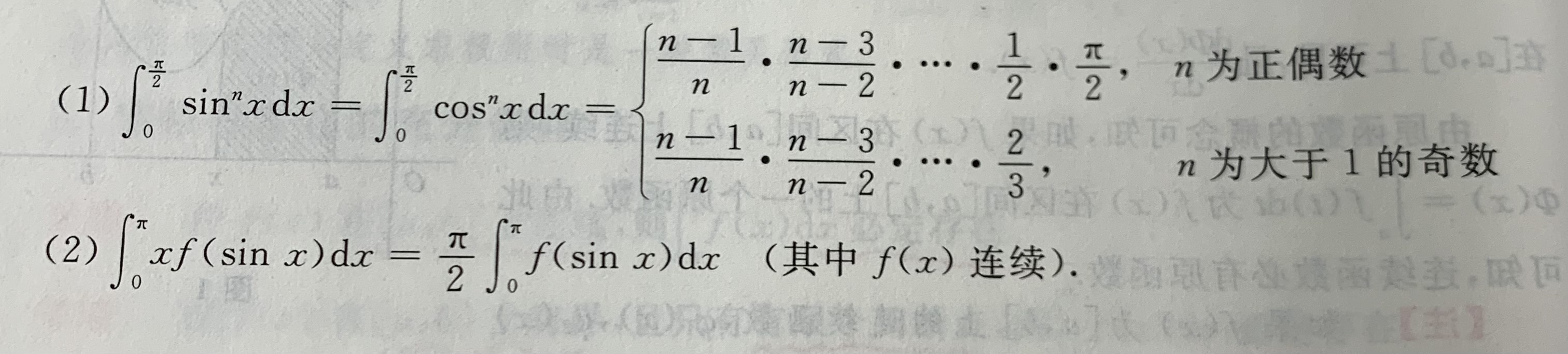
定积分的计算：牛顿-莱布尼茨公式

目录 牛顿-莱布尼茨公式 用C语言代码实现 利用换元积分法和分部积分法 利用奇偶性和周期性求积分 利用已有公式求积分 牛顿-莱布尼茨公式 牛顿-莱布尼茨公式&#xff08;Newton-Leibniz formula&#xff09;是微积分学中的基本定理之一&#xff0c;它反映了定积分与被积函…...

编程日记 2023/9/14 13:44:00

shell脚本之case 的用法

shell脚本之case case是Shell脚本中的一种控制流语句&#xff0c;它允许根据变量的值选择不同的执行路径。case语句的语法如下&#xff1a; case word in pattern [| pattern]...) command-list ;; pattern [| pattern]...) command-list ;; ... *) command-list ;; esa…...

编程日记 2023/9/14 13:42:59

第3章 helloworld 驱动实验（iTOP-RK3568开发板驱动开发指南 ）

在学习C语言或者其他语言的时候&#xff0c;我们通常是打印一句“helloworld”来开启编程世界的大门。学习驱动程序编程亦可以如此&#xff0c;使用helloworld作为我们的第一个驱动程序。 接下来开始编写第一个驱动程序—helloworld。 3.1 驱动编写 本小节来编写一个最简单的…...

编程日记 2023/9/14 13:40:57

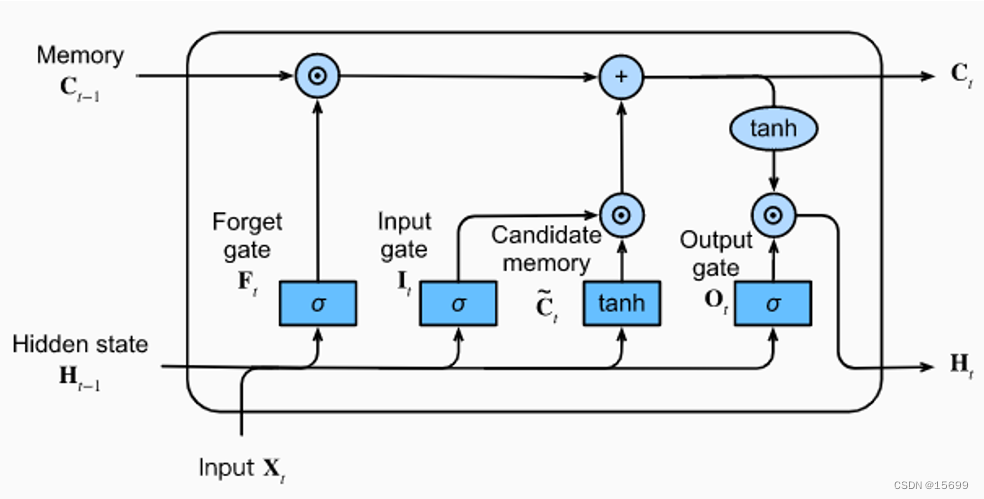
基于PyTorch使用LSTM实现新闻文本分类任务

本文参考 PyTorch深度学习项目实战100例 https://weibaohang.blog.csdn.net/article/details/127154284?spm1001.2014.3001.5501 文章目录 本文参考任务介绍做数据的导入 环境介绍导入必要的包介绍torchnet和keras做数据的导入给必要的参数命名加载文本数据数据前处理模型训…...

编程日记 2023/9/14 13:39:57

Flutter插件的制作和发布

Flutter制作插件有两种方式&#xff08;以下以android和ios为例&#xff09;&#xff1a; 目录 1.直接在主工程下的android和ios项目内写插件代码&#xff1a;2.创建独立Flutter Plugin项目&#xff0c;制作各端插件后&#xff0c;再引入项目&#xff1a;1. 创建Flutter Plugin…...

编程日记 2023/9/14 13:36:54

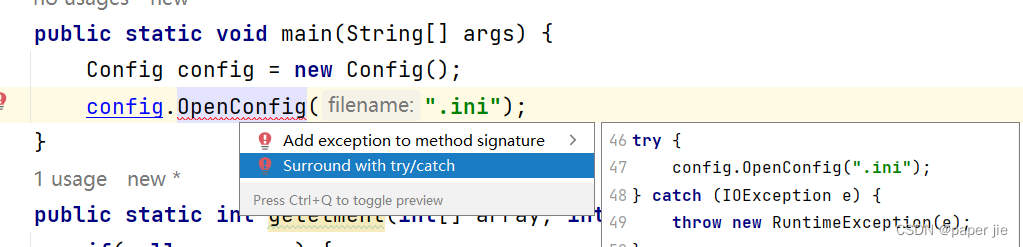
【JAVA】异常

作者主页&#xff1a;paper jie 的博客 本文作者&#xff1a;大家好&#xff0c;我是paper jie&#xff0c;感谢你阅读本文&#xff0c;欢迎一建三连哦。 本文录入于《JAVASE语法系列》专栏&#xff0c;本专栏是针对于大学生&#xff0c;编程小白精心打造的。笔者用重金(时间和…...

编程日记 2023/9/14 13:31:50

合同矩阵充要条件

两个实对称矩阵合同的充要条件是它们的正负惯性指数相同。 正惯性指数是矩阵正特征值个数&#xff0c;负惯性指数是矩阵负特征值个数。 即合同矩阵的充分必要条件是特征值的正负号个数相同。 证明&#xff1a; 本论证中的所有矩阵都是对称矩阵。 根据定义&#xff0c;若矩…...

编程日记 2023/9/14 13:28:46

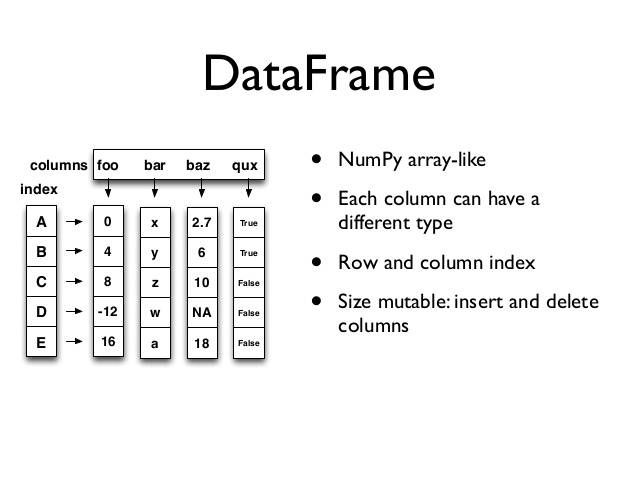
数据分析三剑客之Pandas

1.引入 前面一篇文章我们介绍了numpy&#xff0c;但numpy的特长并不是在于数据处理&#xff0c;而是在它能非常方便地实现科学计算&#xff0c;所以我们日常对数据进行处理时用的numpy情况并不是很多&#xff0c;我们需要处理的数据一般都是带有列标签和index索引的&#xff0…...

编程日记 2023/9/14 13:27:45

Spring Boot自动装配原理

简介 Spring Boot是一个开源的Java框架&#xff0c;旨在简化Spring应用程序的搭建和开发。它通过自动装配的机制&#xff0c;大大减少了繁琐的配置工作&#xff0c;提高了开发效率。本文将深入探讨Spring Boot的自动装配原理。 自动装配的概述 在传统的Spring框架中&#xf…...

编程日记 2023/9/14 13:23:41

VMware Workstation虚拟机网络配置及配置自动启动

目录 一、网络配置二、配置自动启动1.VMware 中配置虚拟机自启动2.系统服务中配置 VMware 服务自启动 一、网络配置 本文将虚拟机 IP 与主机 IP 设置为同一个网段。 点击 “编辑” -> “虚拟网络编辑器(N)…”&#xff1a; 点击 “更改设置”&#xff1a; 将 VMnet0 设置…...

编程日记 2023/9/14 13:19:37

智能语音机器人竞品调研

一、腾讯云-智能客服机器人 链接地址&#xff1a;智能客服机器人_在线智能客服_智能客服解决方案 - 腾讯云 二、阿里云-智能语音机器人 链接地址&#xff1a;智能对话机器人-阿里云帮助中心 链接地址&#xff1a;智能外呼机器人的业务架构_智能外呼机器人-阿里云帮助中心 三、火…...

编程日记 2023/9/14 13:17:36

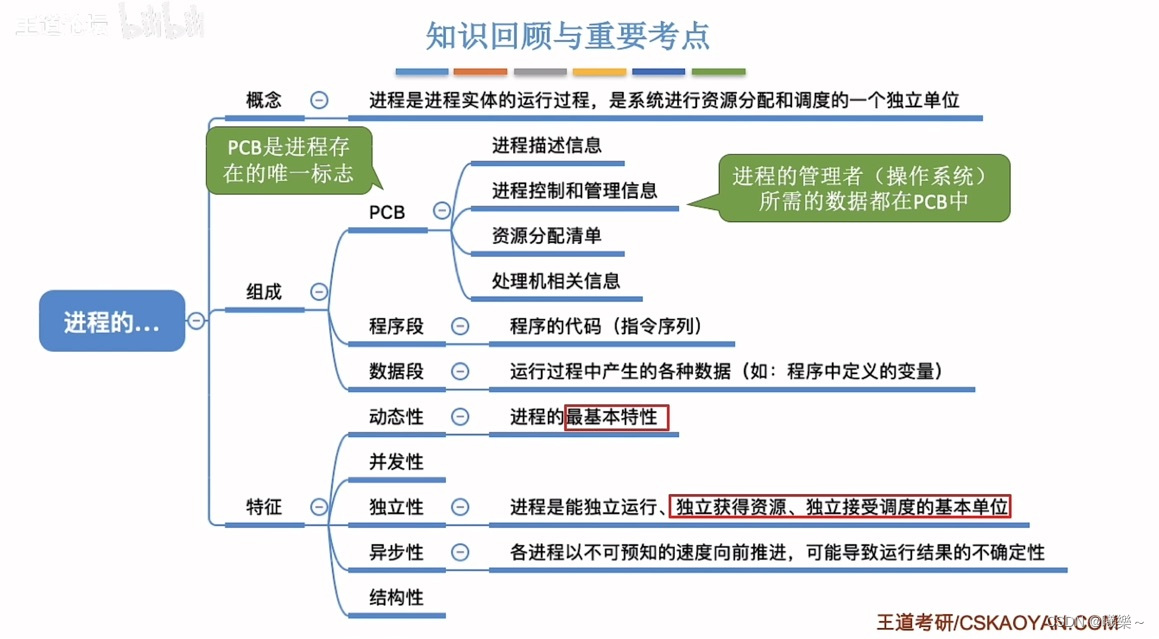
【操作系统】进程的概念、组成、特征

概念组成 程序&#xff1a;静态的放在磁盘&#xff08;外存&#xff09;里的可执行文件&#xff08;代码&#xff09; 作业&#xff1a;代码&#xff0b;数据&#xff0b;申请&#xff08;JCB&#xff09;&#xff08;外存&#xff09; 进程&#xff1a;程序的一次执行过程。 …...

编程日记 2023/9/14 13:16:35

大二第二周总结

问题&#xff1a; 想到了之前追的辩论赛&#xff0c;主题是“被误解是表达者的宿命”&#xff0c; 反方认为被误解不是表达者的宿命&#xff1a; 由于表达者表意含混造成误解的可能性是人力可控的&#xff0c;表达者可在真诚沟通的基础之上&#xff0c;根据对方反应不断调整…...

编程日记 2023/9/14 13:12:29

JDK、eclipse软件的安装

一、打开JDK安装包 二、复制路径 三、点击我的电脑&#xff0c;找到环境变量 四、新建环境 变量名&#xff1a;JAVA_HOME 变量值就是刚刚复制的路径 五、在path中建立新变量 双击path 打印以下文字 最后一直双击确定&#xff0c;安装环境完成。 六、双击eclipse 选择好安装…...

编程日记 2023/9/14 13:10:27

235. 二叉搜索树的最近公共祖先 Python

文章目录 一、题目描述示例 1示例 2 二、代码三、解题思路 一、题目描述 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为&#xff1a;“对于有根树 T 的两个结点 p、q&#xff0c;最近公共祖先表示为一个结点 x&#xff0c;满足…...

编程日记 2023/9/14 13:09:26

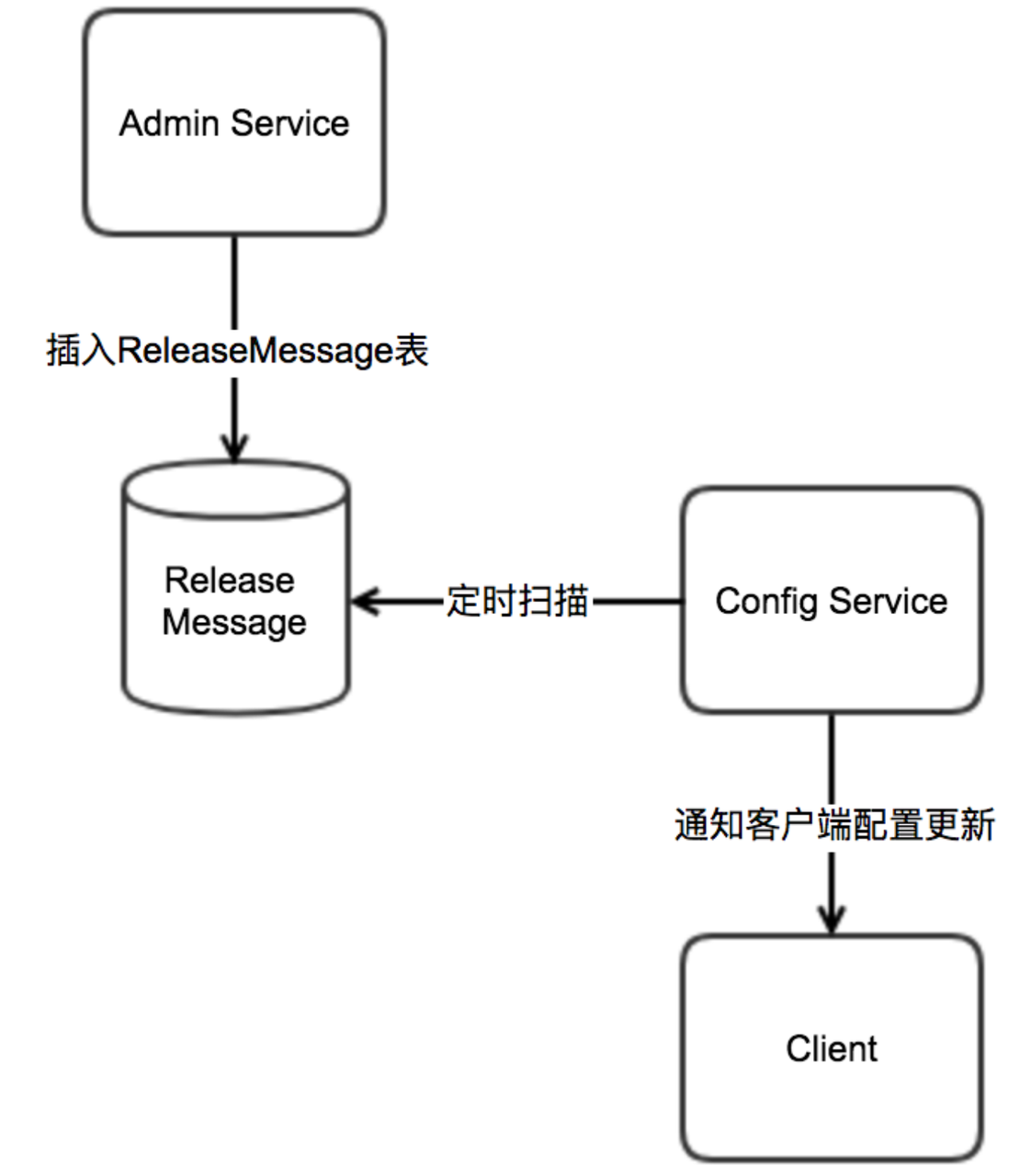
Apollo介绍和入门

文章目录 Apollo介绍配置中心介绍apollo介绍主流配置中心功能特性对比 Apollo简介 入门简单的执行流程Apollo具体的执行流程Apollo对象执行流程分步执行流程 核心概念应用&#xff0c;环境&#xff0c;集群&#xff0c;命名空间企业部署方案灰度发布全量发布 配置发布的原理发送…...

编程日记 2023/9/14 13:06:20

模型参数、模型存储精度、参数与显存

模型参数量衡量单位 M&#xff1a;百万&#xff08;Million&#xff09; B&#xff1a;十亿&#xff08;Billion&#xff09; 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的&#xff0c;但是一个参数所表示多少字节不一定&#xff0c;需要看这个参数以什么…...

编程新知 2025/12/20 12:32:08

PHP和Node.js哪个更爽?

先说结论&#xff0c;rust完胜。 php&#xff1a;laravel&#xff0c;swoole&#xff0c;webman&#xff0c;最开始在苏宁的时候写了几年php&#xff0c;当时觉得php真的是世界上最好的语言&#xff0c;因为当初活在舒适圈里&#xff0c;不愿意跳出来&#xff0c;就好比当初活在…...

编程新知 2025/9/14 7:59:52

23-Oracle 23 ai 区块链表（Blockchain Table）

小伙伴有没有在金融强合规的领域中遇见&#xff0c;必须要保持数据不可变&#xff0c;管理员都无法修改和留痕的要求。比如医疗的电子病历中&#xff0c;影像检查检验结果不可篡改行的&#xff0c;药品追溯过程中数据只可插入无法删除的特性需求&#xff1b;登录日志、修改日志…...

编程新知 2026/1/27 3:40:30

从零实现STL哈希容器：unordered_map/unordered_set封装详解

本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说&#xff0c;直接开始吧&#xff01; 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

编程新知 2026/1/31 12:47:25

2025盘古石杯决赛【手机取证】

前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来&#xff0c;实在找不到&#xff0c;希望有大佬教一下我。 还有就会议时间&#xff0c;我感觉不是图片时间&#xff0c;因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

编程新知 2026/1/29 17:12:17

CMake控制VS2022项目文件分组

我们可以通过 CMake 控制源文件的组织结构，使它们在 VS 解决方案资源管理器中以“组”（Filter）的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总（共4种） 方法描述是否推荐…...

编程新知 2025/12/4 15:47:17

基于SpringBoot在线拍卖系统的设计和实现

摘 要 随着社会的发展&#xff0c;社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统&#xff0c;主要的模块包括管理员&#xff1b;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

编程新知 2026/1/26 13:25:02

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2026/1/30 3:24:00

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师（题目+回答）

安全领域各种资源&#xff0c;学习文档&#xff0c;以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具&#xff0c;欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

编程新知 2026/1/27 2:41:27

快刀集(1): 一刀斩断视频片头广告

一刀流&#xff1a;用一个简单脚本&#xff0c;秒杀视频片头广告&#xff0c;还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农&#xff0c;平时写代码之余看看电影、补补片&#xff0c;是再正常不过的事。 电影嘛&#xff0c;要沉浸&#xff0c;…...

编程新知 2026/1/8 0:40:27