2月10日刷题总结
编辑距离
题目描述
设 AA 和 BB 是两个字符串。我们要用最少的字符操作次数,将字符串 AA 转换为字符串 BB。这里所说的字符操作共有三种:
删除一个字符;
插入一个字符;
将一个字符改为另一个字符。
A, BA,B 均只包含小写字母。
输入格式
第一行为字符串 AA;第二行为字符串 BB;字符串 A, BA,B 的长度均小于 20002000。
输出格式
只有一个正整数,为最少字符操作次数。
输入输出样例
输入 #1复制
sfdqxbw
gfdgw
输出 #1复制
4
说明/提示
对于 100 \%100% 的数据,1 \le |A|, |B| \le 20001≤∣A∣,∣B∣≤2000。
思路:第一步确定dp数组的含义:以i-1结尾和j-1结尾的串相同所要操作的最小次数
第二步寻找状态转移方程,寻找状态转移方程的时候我们先要知道删除和增添操作所产生的效果是一样的,例如abcde和abc要变成相同的字符串,我们可以在串一删除,也可以在串二中增添,也可以串一增添,串二删除同时操作,所以我们可以找到:
if(a1[i]==a2[j])dp[i][j]=dp[i-1][j-1]//相等的情况
else //不相等的情况需要进行操作
dp[i][j]=min(dp[i][j-1]+1dp[i-1][j],dp[i-1][j-1])//分别对应删除串2,删除串1,和替换操作
第三步初始化:dp[0][i]=i,dp[i][0]=i;
code:
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<math.h>
int min_(int x,int y,int z)
{if(y>x)y=x;if(z>y)z=y;return z;
}
int main()
{char s1[2005],s2[2005];scanf("%s",s1);scanf("%s",s2);int dp[2005][2005];int n=strlen(s1),m=strlen(s2);//初始化for(int i=0;i<=n;i++){dp[i][0]=i;}for(int i=0;i<m;i++){dp[0][i]=i;}//dp过程for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(s1[i-1]==s2[j-1])dp[i][j]=dp[i-1][j-1];//相等则不用删除和替换操作else{dp[i][j]=min_(dp[i][j-1]+1,dp[i-1][j]+1,dp[i-1][j-1]+1);//不相等的情况删除和替换}}}printf("%d",dp[n][m]);
}最长递增子序列
题目描述
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3]
输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7]
输出:1
提示:
1 <= nums.length <= 2500
-104 <= nums[i] <= 104
思路:
第一步找dp数组的含义:i(包括i)的最小上升子序列;
第二步找状态转移方程:if(nums[i]<nums[j])dp[i]=max(dp[j]+1,dp[i]);
第三步初始化:因为所有的位置自身也是一个序列。所以dp全部初始化为1;
code:
class Solution
{
public:int lengthOfLIS(vector<int>& nums){vector<int> dp(2505,1);//全部初始化为1int n=nums.size();int ans=0;if(n<=1)return n;//特判一下数组长度为1和0for(int i=1;i<n;i++){for(int j=0;j<i;j++){if(nums[i]>nums[j])//此时为递增{dp[i]=max(dp[j]+1,dp[i]);}}if(ans<dp[i])ans=dp[i];}return ans;}
};最长连续递增序列
题目描述
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:
输入:nums = [1,3,5,4,7]
输出:3
解释:最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
示例 2:
输入:nums = [2,2,2,2,2]
输出:1
解释:最长连续递增序列是 [2], 长度为1。
提示:
1 <= nums.length <= 104
-109 <= nums[i] <= 109
思路:
第一步找dp数组的含义:dp数组:i(包括i)之前的字符最大连续序列的个数
第二步找状态转移方程:if(a[i]>a[i-1])dp[i]=dp[i]+1,dp[i-1];
第三步初始化:
code:
class Solution
{
public:int findLengthOfLCIS(vector<int>& nums) {int n=nums.size(),ans=0;vector<int>dp(n,1);if(n<=1)return 1;for(int i=1;i<n;i++){if(nums[i-1]<nums[i]){dp[i]=dp[i-1]+1;}ans=max(ans,dp[i]);}return ans;}
};最长重复子数组
题目描述
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。
示例 2:
输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc" ,它的长度为 3 。
示例 3:
输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0 。
提示:
1 <= text1.length, text2.length <= 1000
text1 和 text2 仅由小写英文字符组成。
思路:
第一步确定dp数组的含义:dp[i][j]:下标i - 1为结尾的A,和以下标j - 1为结尾的B,最长重复⼦数组长度。
第二步找状态转移方程:
if(a1[i]==a2[j])dp[i][j]=dp[i-1][j-1]
else dp[i][j]=dp[i-1][j],dp[i][j-1]
第三步初始化:因为空串不会和另一个串有公共子数组,所以我们初始化为0即可
code:
class Solution
{
public:int findLength(vector<int>& nums1, vector<int>& nums2) {int dp[1005][1005]={0},n,m,ans=-1;n=nums1.size();m=nums2.size();if(n==1)return 0; for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(nums1[i-1]==nums2[j-1]){dp[i][j]=dp[i-1][j-1]+1;}ans=max(ans,dp[i][j]);}}return ans;}
};最长公共子序列
题目描述
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。
示例 2:
输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc" ,它的长度为 3 。
示例 3:
输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0 。
提示:
1 <= text1.length, text2.length <= 1000
text1 和 text2 仅由小写英文字符组成。
思路:
第一步我们确定dp[i][j]的含义:长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共⼦序列。
第二步找状态转移方程:
if(text1[i-1]==text2[j-1]) dp[i][j]=dp[i-1][j-1]+1;
else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
第三步初始化:同最大子数组一样,全部初始化为0;
code:
class Solution
{
public:int longestCommonSubsequence(string text1, string text2) {int dp[1005][1005]={0};int n=text1.size();int m=text2.size();for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(text1[i-1]==text2[j-1]){dp[i][j]=dp[i-1][j-1]+1;}else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}return dp[n][m];}
};相关文章:

2月10日刷题总结
编辑距离题目描述设 AA 和 BB 是两个字符串。我们要用最少的字符操作次数,将字符串 AA 转换为字符串 BB。这里所说的字符操作共有三种:删除一个字符;插入一个字符;将一个字符改为另一个字符。A, BA,B 均只包含小写字母。输入格式第…...
C++学习/温习:新型源码学编程(三)
写在前面(祝各位新春大吉!兔年如意!) 【本文持续更新中】面向初学者撰写专栏,个人原创的学习C/C笔记(干货)所作源代码输出内容为中文,便于理解如有错误之处请各位读者指正请读者评论回复、参与投票…...

阿里云ecs服务器搭建CTFd(ubuntu20)
1.更新apt包索引 sudo apt-get update更新源 1、使用快捷键【ctrlaltt】打开终端。 2、输入以下命令备份原有软件源文件。 cp /etc/apt/sources.list /etc/apt/sources.list.bak_yyyymmdd 3、再输入以下命令打开sources.list文件并添加新的软件源地址。 vim /etc/apt/sources.…...
视频号小店新订单如何实时同步企业微信
随着直播带货的火热,视频号小店也为商家提供商品信息服务、商品交易,支持商家在视频号运营电商,许多企业也将产品的零售路径渗透至视频号小店中了。如果我们希望在视频号小店接收到订单后,能尽快及时发货,给用户较好的…...

ag-Grid Enterprise
ag-Grid Enterprise Ag-Grid被描述为一种商业产品,已在EULA下分发,它非常先进,性能就像Row分组一样,还有范围选择、master和case、行的服务器端模型等等。 ag Grid Enterprise的巨大特点: 它具有以下功能和属性&#x…...

扫雷——C语言【详解+全部码源】
前言:今天我们学习的是C语言中另一个比较熟知的小游戏——扫雷 下面开始我们的学习吧! 文章目录游戏整体思路游戏流程游戏菜单的打印创建数组并初始化布置雷排查雷完整代码game.hgame.ctest.c游戏整体思路 我们先来看一下网上的扫雷游戏怎么玩 需要打印…...
【C++】类和对象(下)
文章目录1. 再谈构造函数1.1 初始化列表1.2 explicit关键字2. static成员2.1 概念2.2 特性3. 友元3.1 友元函数3.1 友元类4. 内部类5. 匿名对象6. 拷贝对象时的一些编译器优化7. 再次理解类和对象1. 再谈构造函数 1.1 初始化列表 在创建对象时,编译器通过调用构造…...

计算机网络
TCP和UDP TCP如何保证传输的可靠性 基于数据块传输:应用数据被分割成TCP认为最适合的数据块,传输给网络层,称为报文段连接管理:三次握手和四次挥手对失序数据包重新排序以及去重:每个数据包有一个序列号,…...
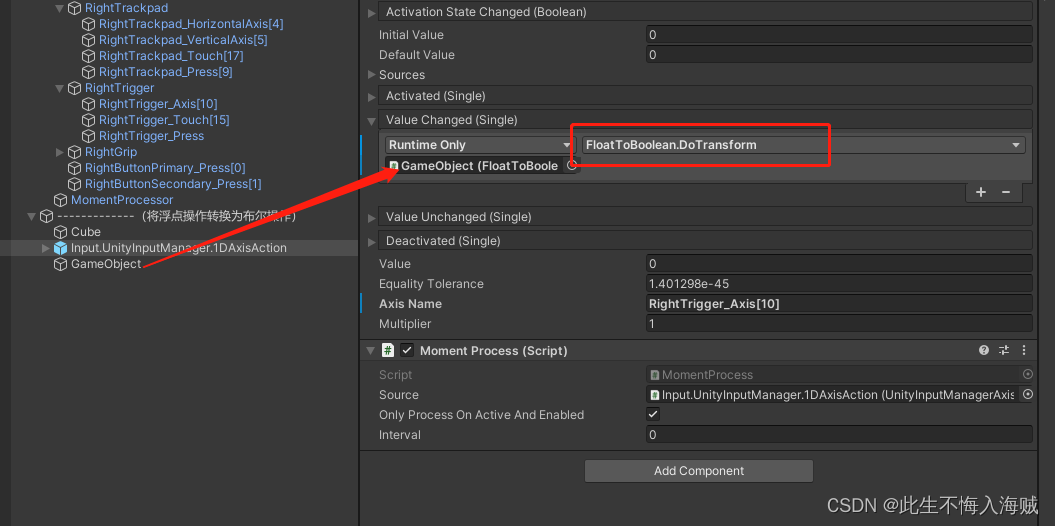
【Unity VR开发】结合VRTK4.0:将浮点操作转换为布尔操作
语录: 奈何桥上奈何愁,奈何桥下浣溪流,奈何人人奈何泪,奈何奈何洗春秋。 前言: 有时,您可能希望使用 一个值来激活或停用操作类型。例如,按下控制器上的扳机轴会导致在完全按下扳机时发生操作。…...

error when starting dev server:Error: Failed to resolve vue/compiler-sfc.
对于node 的包管理工具,我一般习惯用 yarn,但是最近使用 yarn 创建前端项目的时候出了一些问题。yarn create vite vite-project报错如下:error when starting dev server:Error: Failed to resolve vue/compiler-sfc.vitejs/plugin-vue requ…...
Vue2之完整基础介绍和指令与过滤器
Vue2之基础介绍和指令与过滤器一、简介1、概念2、vue的两个特性2.1 数据驱动视图2.2 双向数据绑定3、MVVM二、vue基础用法1、导入vue.js的script脚本文件2、在页面中声明一个将要被vue所控制的DOM区域3、创建vm实例对象(vue实例对象)4、样例完整代码三、…...

JY-7A/3DK/220 19-130V静态【电压继电器】
系列型号 JY-7A/1DK不带辅助电源电压继电器;JY-7B/1DK不带辅助电源电压继电器; JY-7/1DK/120不带辅助电源电压继电器;JY-7/1DK/120不带辅助电源电压继电器; JY-7A/1DKQ不带辅助电源电压继电器;JY-7B/1DKQ不带辅助电源…...

[ECCV 2018] Learning to Navigate for Fine-grained Classification
Contents MethodNavigator-Teacher-Scrutinizer Network (NTS-Net)Navigator and TeacherScrutinizerNetwork architectureJoint training algorithmExperimentReferencesMethod Navigator-Teacher-Scrutinizer Network (NTS-Net) Approach Overview:NTS-Net 在不使用额外的 …...

关于apifox和postman接口工具我有话要说~~
Apifox 和 Postman 都是流行的接口测试工具,各自有其优势和缺点。Apifox 的优势在于它提供了强大的可视化界面,可以方便地测试和监控 API。它还支持多种请求方式,并且支持对请求和响应进行代码生成。但是,Apifox 的缺点在于它不太…...

Vue3通透教程【二】更高效的构建工具—Vite
文章目录🌟 写在前面🌟 webpack🌟 Vite是什么?🌟 使用Vite创建项目🌟 写在最后🌟 写在前面 专栏介绍: 凉哥作为 Vue 的忠实 粉丝输出过大量的 Vue 文章,应粉丝要求开始更…...

前端中如何判断在线状态?
判断在线状态为了判断浏览器的在线状态,HTML5提供了两种方法来检测是否在线。(1)onLine属性:通过navigator对象的onLine属性可返回当前是否在线。如果返回true,则表示在线;如果返回false,则表示…...

[MySQL教程①] - MySQL的安装
目录 ❤ Windows下安装MySQL ❤ 下载mysql installer安装 ❤ 下载zip安装包安装 现在作为服务器操作系统的一般有三种,Windows Server,Linux,Unix,在这里我们只介绍在windows下和linux下安装mysql,Unix下安装应该…...
第八节 Linux 设备树
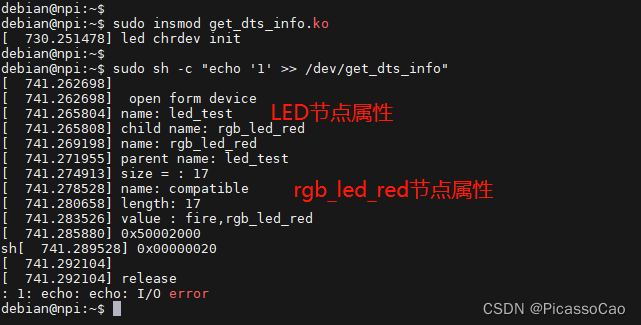
Linux3.x 以后的版本才引入了设备树,设备树用于描述一个硬件平台的板级细节。在早些的linux内核,这些“硬件平台的板级细节”保存在linux 内核目录“/arch”,以ARM 平台为例“硬件平台的板级细节”保存在“/arch/arm/plat-xxx”和“/arch/arm…...
一文了解kafka消息队列,实现kafka的生产者(Producer)和消费者(Consumer)的代码,消息的持久化和消息的同步发送和异步发送
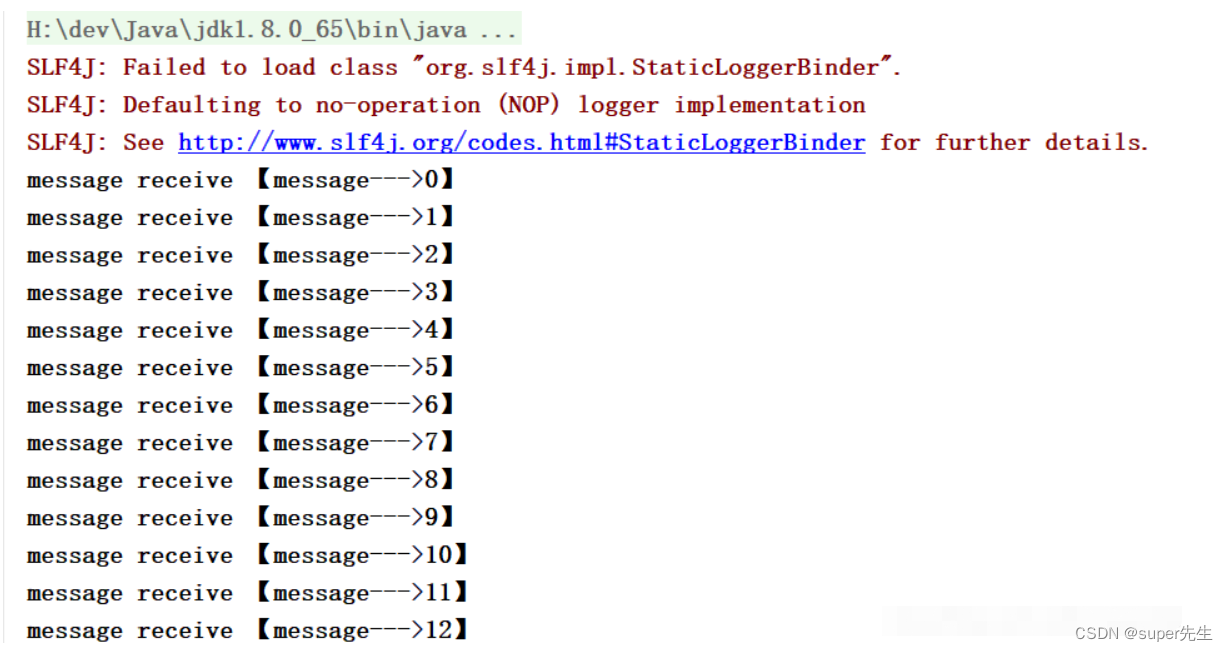
文章目录1. kafka的介绍1.2 Kafka适合的应用场景1.2 Kafka的四个核心API2. 代码实现kafka的生产者和消费者2.1 引入加入jar包2.2 生产者代码2.3 消费者代码2.4 介绍kafka生产者和消费者模式3. 消息持久化4. 消息的同步和异步发送5. 参考文档1. kafka的介绍 最近在学习kafka相关…...
数学建模学习笔记(20)典型相关分析
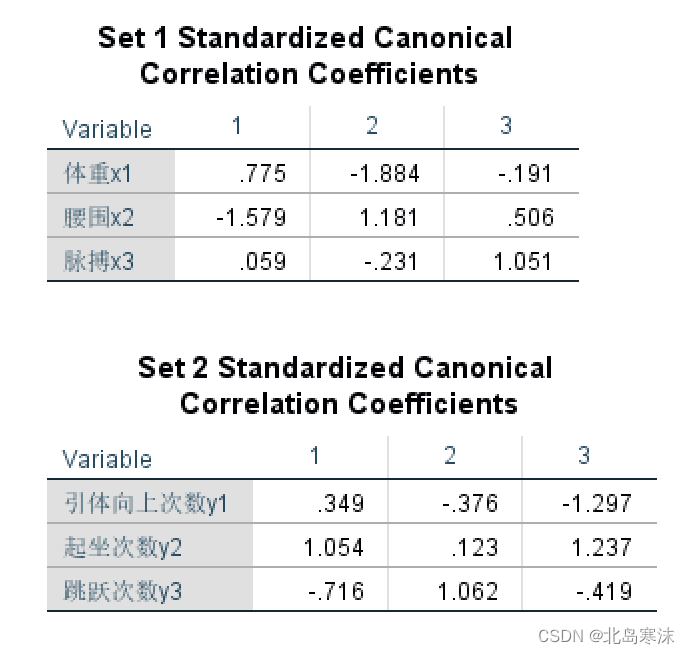
典型相关分析概述:研究两组变量(每组变量都可能有多个指标)之间的相关关系的一种多元统计方法,能够揭示两组变量之间的内在联系。 典型相关分析的思想:把多个变量和多个变量之间的相关化为两个具有代表性的变量之间的…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...
