适合初学者快速入门的Numpy实战全集
适合初学者快速入门的Numpy实战全集
Numpy是一个用python实现的科学计算的扩展程序库,包括:
- 1、一个强大的N维数组对象Array;
- 2、比较成熟的(广播)函数库;
- 3、用于整合C/C++和Fortran代码的工具包;
- 4、实用的线性代数、傅里叶变换和随机数生成函数。numpy和稀疏矩阵运算包scipy配合使用更加方便。
NumPy(Numeric Python)提供了许多高级的数值编程工具,如:矩阵数据类型、矢量处理,以及精密的运算库。专为进行严格的数字处理而产生。多为很多大型金融公司使用,以及核心的科学计算组织如:Lawrence Livermore,NASA用其处理一些本来使用C++,Fortran或Matlab等所做的任务。
本文目录
1.Numpy基本操作
1.1 列表转为矩阵
1.2 维度
1.3 行数和列数()
1.4 元素个数
2.Numpy创建array
2.1 一维array创建
2.2 多维array创建
2.3 创建全零数组
2.4 创建全1数据
2.5 创建全空数组
2.6 创建连续数组
2.7 reshape操作
2.8 创建连续型数据
2.9 linspace的reshape操作
3.Numpy基本运算
3.1 一维矩阵运算
3.2 多维矩阵运算
3.3 基本计算
4.Numpy索引与切片
5.Numpy array合并
5.1 数组合并
5.2 数组转置为矩阵
5.3 多个矩阵合并
5.4 合并例子2
6.Numpy array分割
6.1 构造3行4列矩阵
6.2 等量分割
6.3 不等量分割
6.4 其他的分割方式
7.Numpy copy与 =
7.1 =赋值方式会带有关联性
7.2 copy()赋值方式没有关联性
8.广播机制
9.常用函数
1.Numpy基本操作
1.1 列表转为矩阵
import numpy as np
array = np.array([[1,3,5],[4,6,9]
])print(array)
[[1 3 5][4 6 9]]
1.2 维度
print('number of dim:', array.ndim)
number of dim: 2
1.3 行数和列数()
print('shape:',array.shape)
shape: (2, 3)
1.4 元素个数
print('size:',array.size)
size: 6
2.Numpy创建array
2.1 一维array创建
import numpy as np
# 一维array
a = np.array([2,23,4], dtype=np.int32) # np.int默认为int32
print(a)
print(a.dtype)
[ 2 23 4]
int32
2.2 多维array创建
# 多维array
a = np.array([[2,3,4],[3,4,5]])
print(a) # 生成2行3列的矩阵
[[2 3 4][3 4 5]]
2.3 创建全零数组
a = np.zeros((3,4))
print(a) # 生成3行4列的全零矩阵
[[0. 0. 0. 0.][0. 0. 0. 0.][0. 0. 0. 0.]]
2.4 创建全1数据
# 创建全一数据,同时指定数据类型
a = np.ones((3,4),dtype=np.int)
print(a)
[[1 1 1 1][1 1 1 1][1 1 1 1]]C:\Users\48125\AppData\Local\Temp\ipykernel_18880\1001327096.py:2: DeprecationWarning: `np.int` is a deprecated alias for the builtin `int`. To silence this warning, use `int` by itself. Doing this will not modify any behavior and is safe. When replacing `np.int`, you may wish to use e.g. `np.int64` or `np.int32` to specify the precision. If you wish to review your current use, check the release note link for additional information.
Deprecated in NumPy 1.20; for more details and guidance: https://numpy.org/devdocs/release/1.20.0-notes.html#deprecationsa = np.ones((3,4),dtype=np.int)
2.5 创建全空数组
# 创建全空数组,其实每个值都是接近于零的数
a = np.empty((3,4))
print(a)
[[0. 0. 0. 0.][0. 0. 0. 0.][0. 0. 0. 0.]]
2.6 创建连续数组
# 创建连续数组
a = np.arange(10,21,2) # 10-20的数据,步长为2
print(a)
[10 12 14 16 18 20]
2.7 reshape操作
# 使用reshape改变上述数据的形状
b = a.reshape((2,3))
print(b)
[[10 12 14][16 18 20]]
2.8 创建连续型数据
# 创建线段型数据
a = np.linspace(1,10,20) # 开始端1,结束端10,且分割成20个数据,生成线段
print(a)
[ 1. 1.47368421 1.94736842 2.42105263 2.89473684 3.368421053.84210526 4.31578947 4.78947368 5.26315789 5.73684211 6.210526326.68421053 7.15789474 7.63157895 8.10526316 8.57894737 9.052631589.52631579 10. ]
2.9 linspace的reshape操作
# 同时也可以reshape
b = a.reshape((5,4))
print(b)
[[ 1. 1.47368421 1.94736842 2.42105263][ 2.89473684 3.36842105 3.84210526 4.31578947][ 4.78947368 5.26315789 5.73684211 6.21052632][ 6.68421053 7.15789474 7.63157895 8.10526316][ 8.57894737 9.05263158 9.52631579 10. ]]
3.Numpy基本运算
3.1 一维矩阵运算
import numpy as np
# 一维矩阵运算
a = np.array([10,20,30,40])
b = np.arange(4)
print(a,b)
[10 20 30 40] [0 1 2 3]
c = a - b
print(c)
[10 19 28 37]
print(a*b) # 若用a.dot(b),则为各维之和
[ 0 20 60 120]
# 在Numpy中,想要求出矩阵中各个元素的乘方需要依赖双星符号 **,以二次方举例,即:
c = b**2
print(c)
[0 1 4 9]
# Numpy中具有很多的数学函数工具
c = np.sin(a)
print(c)
[-0.54402111 0.91294525 -0.98803162 0.74511316]
print(b<2)
[ True True False False]
a = np.array([1,1,4,3])
b = np.arange(4)
print(a==b)
[False True False True]
3.2 多维矩阵运算
a = np.array([[1,1],[0,1]])
b = np.arange(4).reshape((2,2))
print(a)
[[1 1][0 1]]
print(b)
[[0 1][2 3]]
# 多维度矩阵乘法
# 第一种乘法方式:
c = a.dot(b)
print(c)
[[2 4][2 3]]
# 第二种乘法:
c = np.dot(a,b)
print(c)
[[2 4][2 3]]
# 多维矩阵乘法不能直接使用'*'号a = np.random.random((2,4))print(np.sum(a))
4.566073674715756
print(np.min(a))
0.28530553227025357
print(np.max(a))
0.8647092701217907
print("a=",a)
a= [[0.28530553 0.4239227 0.82876104 0.64553364][0.43444521 0.35855996 0.72483633 0.86470927]]
如果你需要对行或者列进行查找运算,
就需要在上述代码中为 axis 进行赋值。
当axis的值为0的时候,将会以列作为查找单元,
当axis的值为1的时候,将会以行作为查找单元。
print("sum=",np.sum(a,axis=1))
sum= [2.18352291 2.38255077]
print("min=",np.min(a,axis=0))
min= [0.28530553 0.35855996 0.72483633 0.64553364]
print("max=",np.max(a,axis=1))
max= [0.82876104 0.86470927]
3.3 基本计算
import numpy as npA = np.arange(2,14).reshape((3,4))
print(A)
[[ 2 3 4 5][ 6 7 8 9][10 11 12 13]]
# 最小元素索引
print(np.argmin(A)) # 0
0
# 最大元素索引
print(np.argmax(A)) # 11
11
# 求整个矩阵的均值
print(np.mean(A)) # 7.5
7.5
print(np.average(A)) # 7.5
7.5
print(A.mean()) # 7.5
7.5
# 中位数
print(np.median(A)) # 7.5
7.5
# 累加
print(np.cumsum(A))
[ 2 5 9 14 20 27 35 44 54 65 77 90]
# 累差运算
B = np.array([[3,5,9],[4,8,10]])
print(np.diff(B))
[[2 4][4 2]]
C = np.array([[0,5,9],[4,0,10]])
print(np.nonzero(B))
print(np.nonzero(C))
(array([0, 0, 0, 1, 1, 1], dtype=int64), array([0, 1, 2, 0, 1, 2], dtype=int64))
(array([0, 0, 1, 1], dtype=int64), array([1, 2, 0, 2], dtype=int64))
# 仿照列表排序
A = np.arange(14,2,-1).reshape((3,4)) # -1表示反向递减一个步长
print(A)
[[14 13 12 11][10 9 8 7][ 6 5 4 3]]
print(np.sort(A))
[[11 12 13 14][ 7 8 9 10][ 3 4 5 6]]
# 矩阵转置
print(np.transpose(A))
[[14 10 6][13 9 5][12 8 4][11 7 3]]
print(A.T)
[[14 10 6][13 9 5][12 8 4][11 7 3]]
print(A)
[[14 13 12 11][10 9 8 7][ 6 5 4 3]]
print(np.clip(A,5,9))
[[9 9 9 9][9 9 8 7][6 5 5 5]]
clip(Array,Array_min,Array_max)
将Array_min<X<Array_max X表示矩阵A中的数,如果满足上述关系,则原数不变。
否则,如果X<Array_min,则将矩阵中X变为Array_min;
如果X>Array_max,则将矩阵中X变为Array_max.
4.Numpy索引与切片
import numpy as np
A = np.arange(3,15)
print(A)
[ 3 4 5 6 7 8 9 10 11 12 13 14]
print(A[3])
6
B = A.reshape(3,4)
print(B)
[[ 3 4 5 6][ 7 8 9 10][11 12 13 14]]
print(B[2])
[11 12 13 14]
print(B[0][2])
5
print(B[0,2])
5
# list切片操作
print(B[1,1:3]) # [8 9] 1:3表示1-2不包含3
[8 9]
for row in B:print(row)
[3 4 5 6]
[ 7 8 9 10]
[11 12 13 14]
# 如果要打印列,则进行转置即可
for column in B.T:print(column)
[ 3 7 11]
[ 4 8 12]
[ 5 9 13]
[ 6 10 14]
# 多维转一维
A = np.arange(3,15).reshape((3,4))
# print(A)
print(A.flatten())
# flat是一个迭代器,本身是一个object属性
[ 3 4 5 6 7 8 9 10 11 12 13 14]
for item in A.flat:print(item)
3
4
5
6
7
8
9
10
11
12
13
14
我们一起来来总结一下,看下面切片取值方式(对应颜色是取出来的结果):
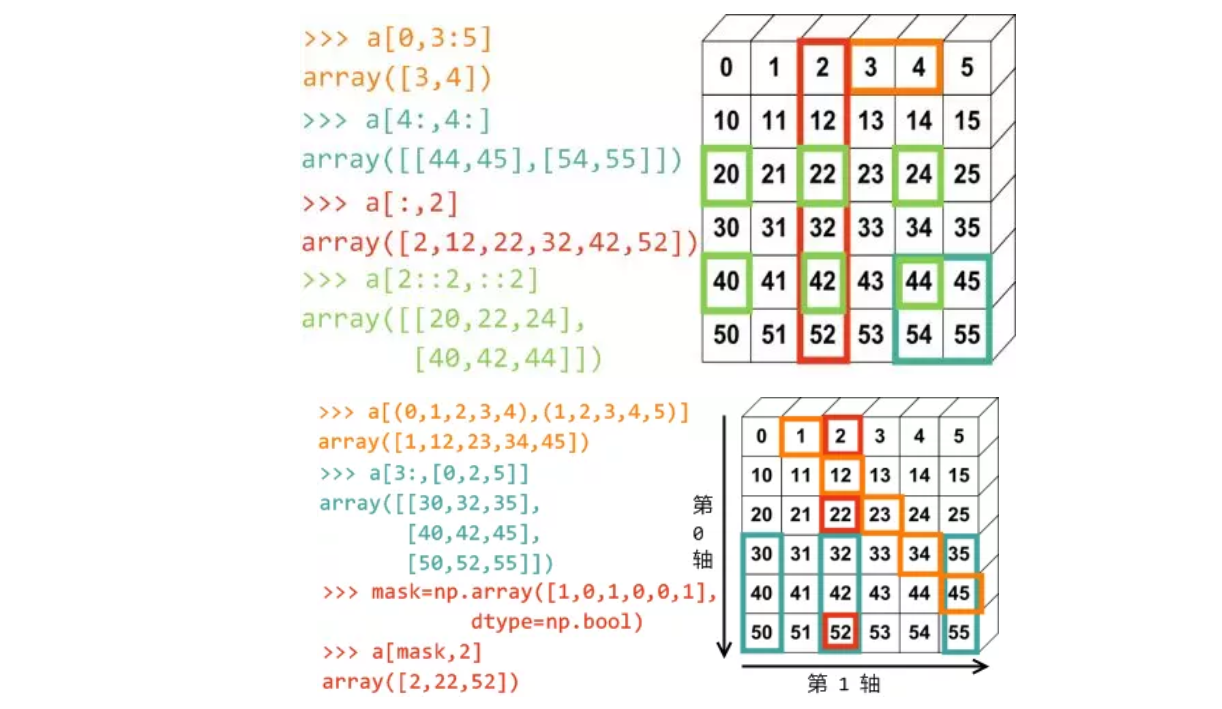
5.Numpy array合并
5.1 数组合并
import numpy as np
A = np.array([1,1,1])
B = np.array([2,2,2])
print(np.vstack((A,B)))
# vertical stack 上下合并,对括号的两个整体操作。
[[1 1 1][2 2 2]]
C = np.vstack((A,B))
print(C)
[[1 1 1][2 2 2]]
print(A.shape,B.shape,C.shape)# 从shape中看出A,B均为拥有3项的数组(数列)
(3,) (3,) (2, 3)
# horizontal stack左右合并
D = np.hstack((A,B))
print(D)
[1 1 1 2 2 2]
print(A.shape,B.shape,D.shape)
# (3,) (3,) (6,)
# 对于A,B这种,为数组或数列,无法进行转置,需要借助其他函数进行转置
(3,) (3,) (6,)
5.2 数组转置为矩阵
print(A[np.newaxis,:]) # [1 1 1]变为[[1 1 1]]
[[1 1 1]]
print(A[np.newaxis,:].shape) # (3,)变为(1, 3)
(1, 3)
print(A[:,np.newaxis])
[[1][1][1]]
5.3 多个矩阵合并
# concatenate的第一个例子
print("------------")
print(A[:,np.newaxis].shape) # (3,1)
------------
(3, 1)
A = A[:,np.newaxis] # 数组转为矩阵
B = B[:,np.newaxis] # 数组转为矩阵
print(A)
[[1][1][1]]
print(B)
[[2][2][2]]
# axis=0纵向合并
C = np.concatenate((A,B,B,A),axis=0)
print(C)
[[1][1][1][2][2][2][2][2][2][1][1][1]]
# axis=1横向合并
C = np.concatenate((A,B),axis=1)
print(C)
[[1 2][1 2][1 2]]
5.4 合并例子2
# concatenate的第二个例子
print("-------------")
a = np.arange(8).reshape(2,4)
b = np.arange(8).reshape(2,4)
print(a)
print(b)
print("-------------")
-------------
[[0 1 2 3][4 5 6 7]]
[[0 1 2 3][4 5 6 7]]
-------------
# axis=0多个矩阵纵向合并
c = np.concatenate((a,b),axis=0)
print(c)
[[0 1 2 3][4 5 6 7][0 1 2 3][4 5 6 7]]
# axis=1多个矩阵横向合并
c = np.concatenate((a,b),axis=1)
print(c)
[[0 1 2 3 0 1 2 3][4 5 6 7 4 5 6 7]]
6.Numpy array分割
6.1 构造3行4列矩阵
import numpy as np
A = np.arange(12).reshape((3,4))
print(A)
[[ 0 1 2 3][ 4 5 6 7][ 8 9 10 11]]
6.2 等量分割
# 等量分割
# 纵向分割同横向合并的axis
print(np.split(A, 2, axis=1))
[array([[0, 1],[4, 5],[8, 9]]), array([[ 2, 3],[ 6, 7],[10, 11]])]
# 横向分割同纵向合并的axis
print(np.split(A,3,axis=0))
[array([[0, 1, 2, 3]]), array([[4, 5, 6, 7]]), array([[ 8, 9, 10, 11]])]
6.3 不等量分割
print(np.array_split(A,3,axis=1))
[array([[0, 1],[4, 5],[8, 9]]), array([[ 2],[ 6],[10]]), array([[ 3],[ 7],[11]])]
6.4 其他的分割方式
# 横向分割
print(np.vsplit(A,3)) # 等价于print(np.split(A,3,axis=0))
[array([[0, 1, 2, 3]]), array([[4, 5, 6, 7]]), array([[ 8, 9, 10, 11]])]
# 纵向分割
print(np.hsplit(A,2)) # 等价于print(np.split(A,2,axis=1))
[array([[0, 1],[4, 5],[8, 9]]), array([[ 2, 3],[ 6, 7],[10, 11]])]
7.Numpy copy与 =
7.1 =赋值方式会带有关联性
import numpy as np
# `=`赋值方式会带有关联性
a = np.arange(4)
print(a) # [0 1 2 3]
[0 1 2 3]
b = a
c = a
d = b
a[0] = 11
print(a) # [11 1 2 3]
[11 1 2 3]
print(b) # [11 1 2 3]
[11 1 2 3]
print(c) # [11 1 2 3]
[11 1 2 3]
print(d) # [11 1 2 3]
[11 1 2 3]
print(b is a) # True
True
print(c is a) # True
True
print(d is a) # True
True
d[1:3] = [22,33]
print(a) # [11 22 33 3]
[11 22 33 3]
print(b) # [11 22 33 3]
[11 22 33 3]
print(c) # [11 22 33 3]
[11 22 33 3]
7.2 copy()赋值方式没有关联性
a = np.arange(4)
print(a) # [0 1 2 3]
[0 1 2 3]
b =a.copy() # deep copy
print(b) # [0 1 2 3]
[0 1 2 3]
a[3] = 44
print(a) # [ 0 1 2 44]
print(b) # [0 1 2 3]# 此时a与b已经没有关联
[ 0 1 2 44]
[0 1 2 3]
8.广播机制
numpy数组间的基础运算是一对一,也就是a.shape==b.shape,但是当两者不一样的时候,就会自动触发广播机制,如下例子:
from numpy import array
a = array([[ 0, 0, 0],[10,10,10],[20,20,20],[30,30,30]])
b = array([0,1,2])
print(a+b)
[[ 0 1 2][10 11 12][20 21 22][30 31 32]]
为什么是这个样子?
这里以tile模拟上述操作,来回到a.shape==b.shape情况!
# 对[0,1,2]行重复3次,列重复1次
b = np.tile([0,1,2],(4,1))
print(a+b)
[[ 0 1 2][10 11 12][20 21 22][30 31 32]]
到这里,我们来给出一张图
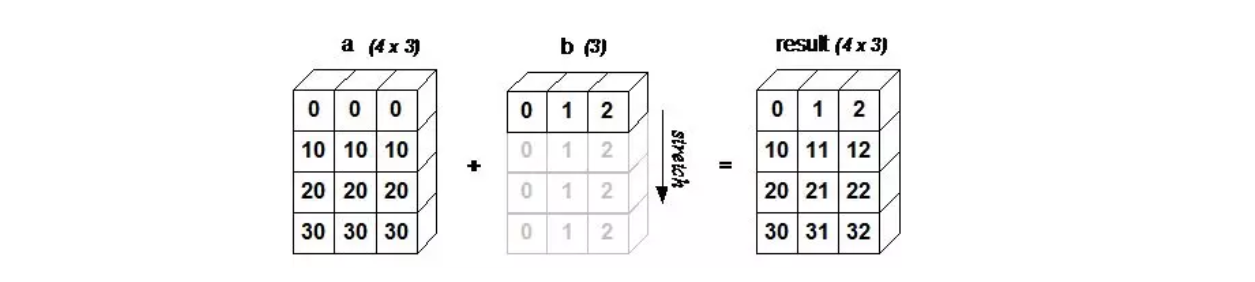
也可以看这张图:

是不是任何情况都可以呢?
当然不是,只有当两个数组的trailing dimensions compatible时才会触发广播,否则报错ValueError: frames are not aligned exception。
上面表达意思是尾部维度必须兼容!
9.常用函数
9.1 np.bincount()
x = np.array([1, 2, 3, 3, 0, 1, 4])
np.bincount(x)
array([1, 2, 1, 2, 1], dtype=int64)
统计索引出现次数:索引0出现1次,1出现2次,2出现1次,3出现2次,4出现1次
因此通过bincount计算出索引出现次数如下:
上面怎么得到的?
对于bincount计算吗,bin的数量比x中最大数多1,例如x最大为4,那么bin数量为5(index从0到4),也就会bincount输出的一维数组为5个数,bincount中的数又代表什么?代表的是它的索引值在x中出现的次数!
还是以上述x为例子,当我们设置weights参数时候,结果又是什么?
这里假定:
w = np.array([0.3,0.5,0.7,0.6,0.1,-0.9,1])
那么设置这个w权重后,结果为多少?
np.bincount(x,weights=w)
array([ 0.1, -0.6, 0.5, 1.3, 1. ])
怎么计算的?
先对x与w抽取出来:
x ---> [1, 2, 3, 3, 0, 1, 4]
w ---> [0.3,0.5,0.7,0.6,0.1,-0.9,1]
索引 0 出现在x中index=4位置,那么在w中访问index=4的位置即可,w[4]=0.1
索引 1 出现在x中index=0与index=5位置,那么在w中访问index=0与index=5的位置即可,然后将两这个加和,计算得:w[0]+w[5]=-0.6
其余的按照上面的方法即可!
bincount的另外一个参数为minlength,这个参数简单,可以这么理解,当所给的bin数量多于实际从x中得到的bin数量后,后面没有访问到的设置为0即可。
还是上述x为例:
这里我们直接设置minlength=7参数,并输出!
np.bincount(x,weights=w,minlength=7)
array([ 0.1, -0.6, 0.5, 1.3, 1. , 0. , 0. ])
与上面相比多了两个0,这两个怎么会多?
上面知道,这个bin数量为5,index从0到4,那么当minlength为7的时候,也就是总长为7,index从0到6,多了后面两位,直接补位为0即可!
9.2 np.argmax()
函数原型为:numpy.argmax(a, axis=None, out=None).
函数表示返回沿轴axis最大值的索引。
x = [[1,3,3],[7,5,2]]
print(np.argmax(x))
3
对于这个例子我们知道,7最大,索引位置为3(这个索引按照递增顺序)!
axis属性
axis=0表示按列操作,也就是对比当前列,找出最大值的索引!
x = [[1,3,3],[7,5,2]]
print(np.argmax(x,axis=0))
[1 1 0]
axis=1表示按行操作,也就是对比当前行,找出最大值的索引!
x = [[1,3,3],[7,5,2]]
print(np.argmax(x,axis=0))
[1 1 0]
那如果碰到重复最大元素?
返回第一个最大值索引即可!
例如:
x = np.array([1, 3, 2, 3, 0, 1, 0])
print(x.argmax())
1
9.3 上述合并实例
这里来融合上述两个函数,举个例子:
x = np.array([1, 2, 3, 3, 0, 1, 4])
print(np.argmax(np.bincount(x)))
1
最终结果为1,为什么?
首先通过np.bincount(x)得到的结果是:[1 2 1 2 1],再根据最后的遇到重复最大值项,则返回第一个最大值的index即可!2的index为1,所以返回1。
9.4 求取精度
np.around([-0.6,1.2798,2.357,9.67,13], decimals=0)#取指定位置的精度
array([-1., 1., 2., 10., 13.])
看到没,负数进位取绝对值大的!
np.around([1.2798,2.357,9.67,13], decimals=1)
array([ 1.3, 2.4, 9.7, 13. ])
np.around([1.2798,2.357,9.67,13], decimals=2)
array([ 1.28, 2.36, 9.67, 13. ])
从上面可以看出,decimals表示指定保留有效数的位数,当超过5就会进位(此时包含5)!
但是,如果这个参数设置为负数,又表示什么?
np.around([1,2,5,6,56], decimals=-1)
array([ 0, 0, 0, 10, 60])
发现没,当超过5时候(不包含5),才会进位!-1表示看一位数进位即可,那么如果改为-2呢,那就得看两位!
np.around([1,2,5,50,56,190], decimals=-2)
array([ 0, 0, 0, 0, 100, 200])
看到没,必须看两位,超过50才会进位,190的话,就看后面两位,后两位90超过50,进位,那么为200!
计算沿指定轴第N维的离散差值
x = np.arange(1 , 16).reshape((3 , 5))
print(x)
[[ 1 2 3 4 5][ 6 7 8 9 10][11 12 13 14 15]]
np.diff(x,axis=1) #默认axis=1
array([[1, 1, 1, 1],[1, 1, 1, 1],[1, 1, 1, 1]])
np.diff(x,axis=0)
array([[5, 5, 5, 5, 5],[5, 5, 5, 5, 5]])
取整
np.floor([-0.6,-1.4,-0.1,-1.8,0,1.4,1.7])
array([-1., -2., -1., -2., 0., 1., 1.])
看到没,负数取整,跟上述的around一样,是向左!
取上限
np.ceil([1.2,1.5,1.8,2.1,2.0,-0.5,-0.6,-0.3])
array([ 2., 2., 2., 3., 2., -0., -0., -0.])
取上限!找这个小数的最大整数即可!
查找
利用np.where实现小于0的值用0填充吗,大于0的数不变!
x = np.array([[1, 0],[2, -2],[-2, 1]])
print(x)
[[ 1 0][ 2 -2][-2 1]]
np.where(x>0,x,0)
array([[1, 0],[2, 0],[0, 1]])
每文一语
加油
相关文章:

适合初学者快速入门的Numpy实战全集
适合初学者快速入门的Numpy实战全集 Numpy是一个用python实现的科学计算的扩展程序库,包括: 1、一个强大的N维数组对象Array;2、比较成熟的(广播)函数库;3、用于整合C/C和Fortran代码的工具包;…...

rabbitmq 面试题
1.交换机类型 RabbitMQ是一个开源的消息队列系统,它支持多种交换机类型,用于在消息的生产者和消费者之间路由和分发消息 Direct Exchange(直接交换机):Direct交换机是最简单的交换机类型之一。它将消息按照消息的Rout…...
比较Visual Studio Code中的文件
目录 一、比较两个文件 1.1VS code中的文件大致分为两类: 1.2如何比较VS code中的两个文件? 二、并排差异模式:VS code中的一种差异模式 三、内联差异模式:VS code中的另一种差异模式 四、VS code忽略在行首或者行尾添加或删除…...

誉天在线项目-UML状态图+泳道图
什么是UML UML(Unified Modeling Language)是一种用于软件系统建模的标准化语言。它提供了一组图形符号和规范,用于描述和设计软件系统的结构、行为和交互。 UML图形符号包括类图、用例图、时序图、活动图、组件图、部署图等,每…...

【linux基础(六)】Linux中的开发工具(中)--gcc/g++
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:Linux从入门到开通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学更多操作系统知识 🔝🔝 Linux中的开发工具 1. 前言2.…...
u盘上面 安装 ubuntu 系统
u盘上面 安装 ubuntu 系统 下载 一个 Ubuntu 22.04.3 LTS 桌面版 https://ubuntu.com/download/desktop 找到一个U盘 参考文章: 把 Ubuntu 装到U盘里随身携带,并同时支持 BIOS 和 UEFI 启动 https://www.luogu.com.cn/blog/GGAutomaton/portable-ubu…...
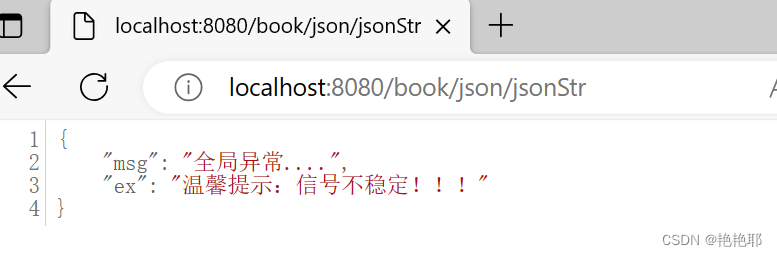
【推荐】SpringMVC与JSON数据返回及异常处理机制的使用
🎬 艳艳耶✌️:个人主页 🔥 个人专栏 :《【推荐】Spring与Mybatis集成整合》 ⛺️ 生活的理想,为了不断更新自己 ! 1.JSON 在SpringMVC中,JSON数据返回通常是通过使用ResponseBody注解将Java对象转换为JSO…...

SpringBoot新增拦截器详解
目录 一、拦截器使用 二、SpringMvc拦截器接口 三、SpringBoot集成拦截器 拦截器(Interceptor)通常是指在软件开发中用于处理请求和响应的中间件组件。拦截器的主要目的是在请求进入某个处理流程或在响应返回给客户端之前执行一些额外的操作或逻辑。 …...

Golang开发--select
在Go语言中,select语句用于在多个通道操作中进行选择。select语句使得程序可以同时等待多个通道的操作,并在其中任意一个通道就绪时执行相应的操作。以下是select语句的详细描述: select { case <-ch1:// 当ch1通道可读时执行的操作 case…...
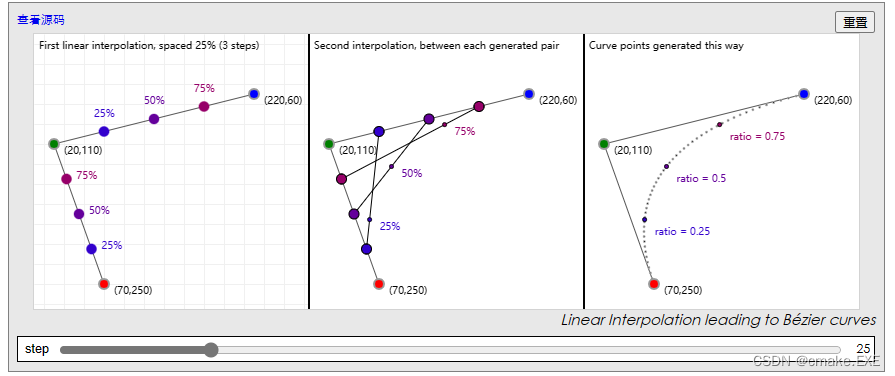
贝塞尔曲线的一些资料收集
一本免费的在线书籍,供你在非常需要了解如何处理贝塞尔相关的事情。 https://pomax.github.io/bezierinfo/zh-CN/index.html An algorithm to find bounding box of closed bezier curves? - Stack Overflow https://stackoverflow.com/questions/2587751/an-algo…...

计算机网络原理 运输层
一,运输层协议概述 1,进程之间的通信 从通信和信息处理的角度看,运输层向它上面的应用层提供通信服务,它属于面向通信部分的最高层,同时也是用户功能中的最底层。当网络边缘部分的两台主机使用网络核心部分的功能进行…...

【JavaEE】多线程案例-阻塞队列
1. 前言 阻塞队列(BlockingQueue)是一个支持两个附加操作的队列。这两个附加的操作是: 在队列为空时,获取元素的线程会等待队列变为非空当队列满时,存储元素的线程会等待队列可用 阻塞队列常用于生产者和消费者的场…...
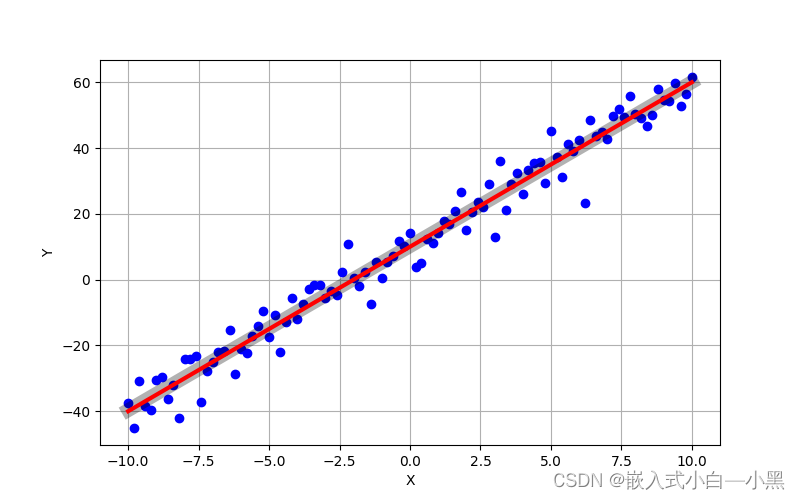
【物联网】简要介绍最小二乘法—C语言实现
最小二乘法是一种常用的数学方法,用于拟合数据和寻找最佳拟合曲线。它的目标是找到一个函数,使其在数据点上的误差平方和最小化。 文章目录 基本原理最小二乘法的求解应用举例使用C语言实现最小二乘法总结 基本原理 假设我们有一组数据点 ( x 1 , y 1 …...

慢查询SQL如何优化
一.什么是慢SQL? 慢SQL指的是Mysql中执行比较慢的SQL,排查慢SQL最常用的方法是通过慢查询日志来查找慢SQL。Mysql的慢查询日志是Mysql提供的一种日志记录,它用来记录Mysql中响应时间超过long_query_time值的sql,long_query_time的默认时间为10s. 二.查看慢SQL是否…...

UART 通信-使用VIO进行板级验证
串口系列知识分享: (1)串口通信实现-串口发送 (2)串口通信发送多字节数据 (3)串口通信实现-串口接收 (4)UART 通信-使用VIO进行板级验证 (5)串口接收-控制LED闪烁 (6)使用串口发送实现ACX720开发板时钟显示 (7)串口发送+RAM+VGA传图 文章目录 前言一、uart串口协…...

linux 查看可支持的shell
查看可支持的shell linux中支持多种shell类型,所以在shell文件的第一行需要指定所使用的shell #!/bin/bash 指定该脚本使用的是/bin/bash,这样的机制使得我们可以轻松地引用任何的解释器 查看该linux系统支持的shell cat /etc/shells/bin/sh/bin/bash/us…...

微服务简介
微服务简介 微服务架构是一种软件架构模式,它将一个大型应用程序拆分为一组小型、独立的服务,每个服务都有自己的业务逻辑和数据存储。这些服务可以独立开发、部署和扩展,通常使用HTTP或其他轻量级通信协议进行通信。 以下是微服务架构的一…...
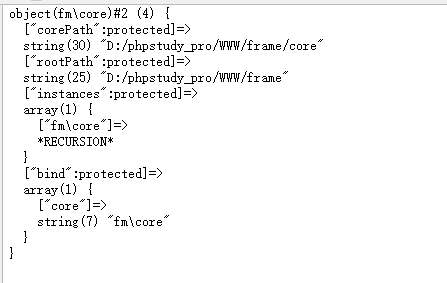
PHP自己的框架2.0设置常量并绑定容器(重构篇三)
目录 1、设置常量并绑定容器 2、容器增加设置当前容器的实例和绑定一个类实例当容器 3、将常量绑定到容器中 4、运行效果 1、设置常量并绑定容器 2、容器增加设置当前容器的实例和绑定一个类实例当容器 //设置当前容器的实例public static function setInstance($instance){…...

重建大师提交空三后引擎状态是等待,怎么开启?
答:图片中这是在自由网空三阶段,整个AT都是等待中,可以修改任务目录和监控目录看一下,先设置引擎,再提交空三。...
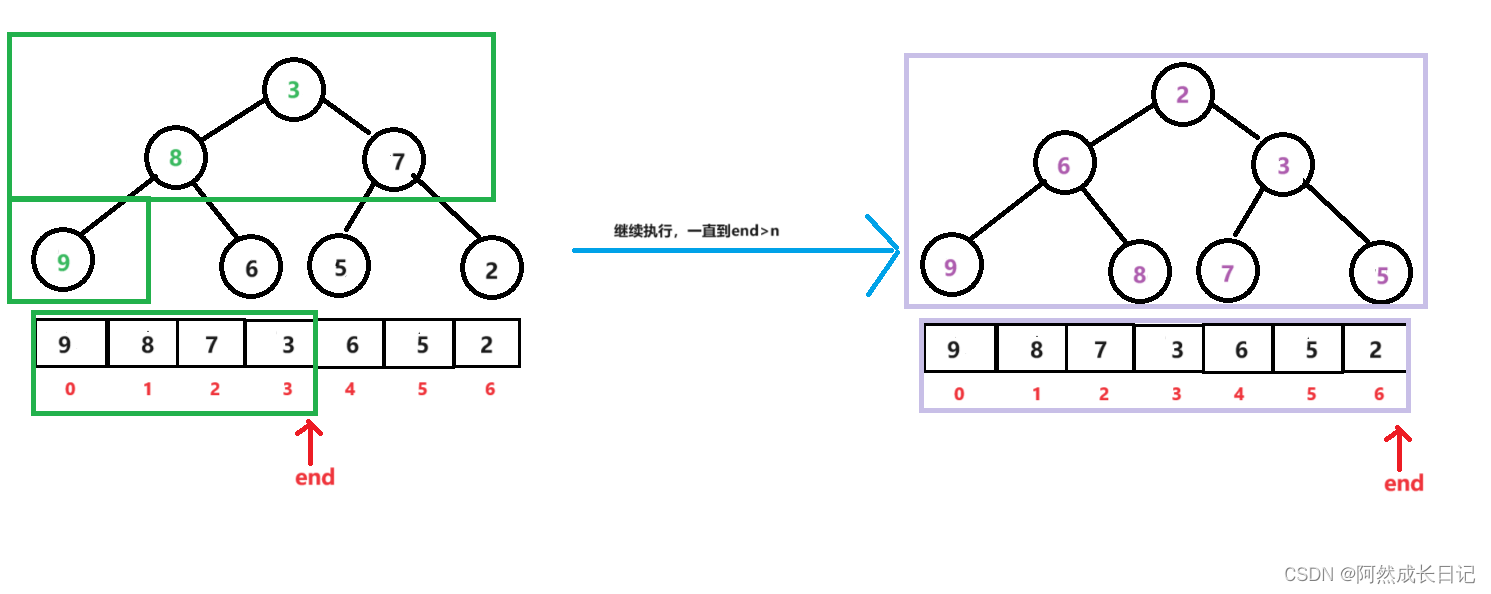
【数据结构】堆的向上调整和向下调整以及相关方法
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃 文章目录 一、堆的概念二、堆的性质…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...
