C++下基于粒子群算法解决TSP问题
粒子群优化算法求解TSP旅行商问题C++(2020.11.12)_jing_zhong的博客-CSDN博客
混合粒子群算法(PSO):C++实现TSP问题 - 知乎 (zhihu.com)
一、原理
又是一个猜答案的算法,和遗传算法比较像,也是设置迭代次数,控制什么时候结束,然后设置粒子种群,每个种群代表一个访问城市的路径,代价函数就是访问一遍的路径和。
初始的时候,随机初始化30个粒子群(可自己设置),然后从这30个例子群里,找一个种群代价最优的结果,存入gbest路径。接着就是每次迭代更新粒子种群,更新思路是每个粒子包含一条访问城市的路径,对每个粒子中的点产生一个速度(这个速度有一共对应公式,v = w * v_cur + c1 * r1 * (x_best - x_cur) +c2 * r2(x_gbest - x_cur)),通过这个速度更新访问城市的路径(x = x + v),当然这个速度作用于城市序号上,会产生小数和重叠,以及不能让这个速度太大,需要限定在一定范围内,如果出现城市序号重复,则需要将重复的序号换成没有出现的序号。
最后每迭代一次,计算一次全局最优粒子,直到迭代结束。
如果访问29个城市,暴力枚举需要计算28!= 304 888 344 611 713 860 501 504 000 000 。可见随着城市数量的增加,计算量是指数级上升,如果使用粒子群算法,计算量30*500=15000,计算量是线性的,确实很有优势。
二、代码
1 1150.0 1760.02 630.0 1660.03 40.0 2090.04 750.0 1100.05 750.0 2030.06 1030.0 2070.07 1650.0 650.08 1490.0 1630.09 790.0 2260.010 710.0 1310.011 840.0 550.012 1170.0 2300.013 970.0 1340.014 510.0 700.015 750.0 900.016 1280.0 1200.017 230.0 590.018 460.0 860.019 1040.0 950.020 590.0 1390.021 830.0 1770.022 490.0 500.023 1840.0 1240.024 1260.0 1500.025 1280.0 790.026 490.0 2130.027 1460.0 1420.028 1260.0 1910.029 360.0 1980.0
#include <iostream>
#include <string>
#include <fstream>
#include <time.h>
#include <random>
using namespace std;
const int citycount = 29;
double vmax = 1, vmin = -1;
std::default_random_engine random(time(NULL));//通过time这个随机数种子,每次产生不同的随机数
static std::uniform_real_distribution<double> distribution(0.0, std::nextafter(1.0, DBL_MAX));// C++11提供的实数均匀分布模板类 0~1
static std::uniform_real_distribution<double> distribution1(vmin, std::nextafter(vmax, DBL_MAX));//-1~1class City
{
public:string name;//城市名称double x, y;//城市点的二维坐标void shuchu(){std::cout << name + ":" << "(" << x << "," << y << ")" << endl;}
};class Graph
{
public:City city[citycount];//城市数组double distance[citycount][citycount];//城市间的距离矩阵void Readcoordinatetxt(string txtfilename)//读取城市坐标文件的函数{ifstream myfile(txtfilename, ios::in);double x = 0, y = 0;int z = 0;if (!myfile.fail()){int i = 0;while (!myfile.eof() && (myfile >> z >> x >> y)){city[i].name = to_string(z);//城市名称转化为字符串city[i].x = x; city[i].y = y;i++;}}elsecout << "文件不存在";myfile.close();//计算城市距离矩阵for (int i = 0; i < citycount; i++)//29for (int j = 0; j < citycount; j++){distance[i][j] = sqrt((pow((city[i].x - city[j].x), 2) + pow((city[i].y - city[j].y), 2)) / 10.0);//计算城市ij之间的伪欧式距离if (round(distance[i][j] < distance[i][j])) distance[i][j] = round(distance[i][j]) + 1;else distance[i][j] = round(distance[i][j]);//round向上取整}}void shuchu(){cout << "城市名称 " << "坐标x" << " " << "坐标y" << endl;for (int i = 0; i < citycount; i++)city[i].shuchu();cout << "距离矩阵: " << endl;for (int i = 0; i < citycount; i++){for (int j = 0; j < citycount; j++){if (j == citycount - 1)std::cout << distance[i][j] << endl;elsestd::cout << distance[i][j] << " ";}}}
};Graph Map_City;//定义全局对象图,放在Graph类后
int * Random_N(int n)
{int *geti;geti = new int[n];int j = 0;while (j < n){while (true){int flag = -1;int temp = rand() % n + 1;//随机取1~29if (j > 0){int k = 0;for (; k < j; k++){if (temp == *(geti + k))break;}if (k == j){*(geti + j) = temp;flag = 1;}}else{*(geti + j) = temp;flag = 1;}if (flag == 1)break;}j++;}return geti;
}double Evaluate(int *x)//计算粒子适应值的函数
{double fitnessvalue = 0;for (int i = 0; i < citycount - 1; i++)fitnessvalue += Map_City.distance[x[i] - 1][x[i + 1] - 1];fitnessvalue += Map_City.distance[x[citycount - 1] - 1][x[0] - 1];//城市尾与第一个城市的距离,x是一组路线的序号return fitnessvalue;
}class Particle
{
public:int *x;//粒子的位置 一条路径int *v;//粒子的速度double fitness;void Init(){x = new int[citycount];v = new int[citycount];int *M = Random_N(citycount);//随机生成一组路径for (int i = 0; i < citycount; i++)x[i] = *(M + i);fitness = Evaluate(x);//计算这组路径的代价for (int i = 0; i < citycount; i++){v[i] = (int)distribution1(random);//产生-1~1之间的随机数}}void shuchu(){for (int i = 0; i < citycount; i++){if (i == citycount - 1)std::cout << x[i] << ") = " << fitness << endl;else if (i == 0)std::cout << "f(" << x[i] << ",";elsestd::cout << x[i] << ",";}}
};void Adjuxt_validParticle(Particle p)//调整粒子有效性的函数,使得粒子的位置符合TSP问题解的一个排列
{int route[citycount];//1-citycountbool flag[citycount];//对应route数组中是否在粒子的位置中存在的数组,参考数组为routeint biaoji[citycount];//对粒子每个元素进行标记的数组,参考数组为粒子位置xfor (int j = 0; j < citycount; j++){route[j] = j + 1;flag[j] = false;biaoji[j] = 0;}//首先判断粒子p的位置中是否有某个城市且唯一,若有且唯一,则对应flag的值为true,for (int j = 0; j < citycount; j++){int num = 0;for (int k = 0; k < citycount; k++){if (p.x[k] == route[j]){biaoji[k] = 1;//说明粒子中的k号元素对应的城市在route中,并且是第一次出现才进行标记num++; break;}}if (num == 0) flag[j] = false;//粒子路线中没有route[j]这个城市else if (num == 1) flag[j] = true;//粒子路线中有route[j]这个城市}for (int k = 0; k < citycount; k++){if (flag[k] == false)//粒子路线中没有route[k]这个城市,需要将这个城市加入到粒子路线中{int i = 0;for (; i < citycount; i++){if (biaoji[i] != 1)break;}p.x[i] = route[k];//对于标记为0的进行替换biaoji[i] = 1;}}
}class PSO
{
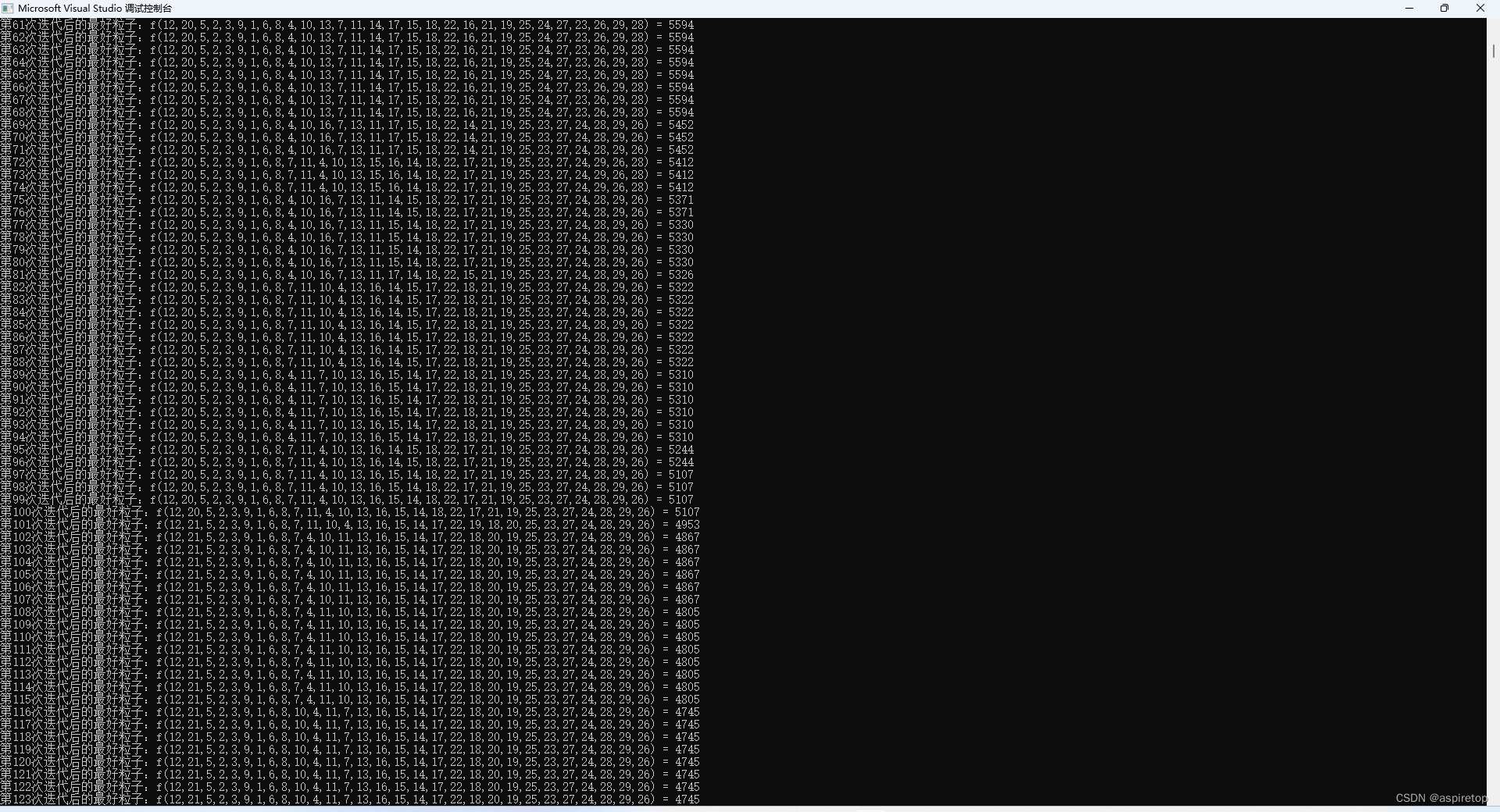
public:Particle *oldparticle; //当前粒子种群信息Particle *pbest; //每个个体最优Particle gbest;//群体最优double c1, c2, w;int Itetime;int popsize;void Init(int Pop_Size, int itetime, double C1, double C2, double W){Itetime = itetime;//迭代500次c1 = C1;//2c2 = C2;//2w = W;//0.8popsize = Pop_Size;//30oldparticle = new Particle[popsize];//30个粒子,每个粒子包含一条随机路径pbest = new Particle[popsize];//30个粒子for (int i = 0; i < popsize; i++)//初始化30次{oldparticle[i].Init();//初始化30个粒子群pbest[i].Init();//初始化30个粒子群for (int j = 0; j < citycount; j++){pbest[i].x[j] = oldparticle[i].x[j];pbest[i].fitness = oldparticle[i].fitness;}}gbest.Init(); //初始化一个粒子群gbest.fitness = INFINITY;//初始设为极大值for (int i = 0; i < popsize; i++)//遍历30个粒子群{if (pbest[i].fitness < gbest.fitness)//如果当前粒子群代价比种群最小的代价还小,则更新其{gbest.fitness = pbest[i].fitness;for (int j = 0; j < citycount; j++)//29个城市点gbest.x[j] = pbest[i].x[j];//最优路径的路径}}}void Shuchu(){for (int i = 0; i < popsize; i++){std::cout << "粒子" << i + 1 << "->";oldparticle[i].shuchu();}std::cout << "当前最优粒子:" << std::endl;gbest.shuchu();}void PSO_TSP(int Pop_size, int itetime, double C1, double C2, double W, double Vlimitabs, string filename){Map_City.Readcoordinatetxt(filename);//计算城市间距离矩阵Map_City.shuchu();//输出初始城市位置和距离矩阵vmax = Vlimitabs; //3vmin = -Vlimitabs;//-3Init(Pop_size, itetime, C1, C2, W);//在随机初始的粒子群中,找到一个最优的粒子std::cout << "初始化后的种群如下:" << endl;Shuchu();//输出初始种群及最优路径//向文件中写入城市坐标,距离矩阵ofstream outfile;outfile.open("result.txt", ios::trunc);outfile << "城市名称 " << "坐标x" << " " << "坐标y" << endl;for (int i = 0; i < citycount; i++)outfile << Map_City.city[i].name << " " << Map_City.city[i].x << " " << Map_City.city[i].y << endl;outfile << "距离矩阵: " << endl;for (int i = 0; i < citycount; i++){for (int j = 0; j < citycount; j++){if (j == citycount - 1)outfile << Map_City.distance[i][j] << endl;elseoutfile << Map_City.distance[i][j] << " ";}}outfile << "初始化后的种群如下:" << endl;for (int i = 0; i < popsize; i++){outfile << "粒子" << i + 1 << "->";for (int j = 0; j < citycount; j++)//29{if (j == citycount - 1)outfile << oldparticle[i].x[j] << ") = " << oldparticle[i].fitness << endl;else if (j == 0)outfile << "f(" << oldparticle[i].x[j] << ",";elseoutfile << oldparticle[i].x[j] << ",";}}for (int ite = 0; ite < Itetime; ite++)//500次{for (int i = 0; i < popsize; i++)//30{//更新粒子速度和位置for (int j = 0; j < citycount; j++)//29{//v= w*v_oldP + c1*r1*(x_bestP - x_oldP) +c2*r2(x_gbest - x_oldP)oldparticle[i].v[j] = (int)(w*oldparticle[i].v[j] + c1 * distribution(random)*(pbest[i].x[j] - oldparticle[i].x[j]) + c2 * distribution(random)*(gbest.x[j] - oldparticle[i].x[j]));if (oldparticle[i].v[j] > vmax)//粒子速度越界调整oldparticle[i].v[j] = (int)vmax;else if (oldparticle[i].v[j] < vmin)oldparticle[i].v[j] = (int)vmin;oldparticle[i].x[j] += oldparticle[i].v[j];//x=x+vif (oldparticle[i].x[j] > citycount)oldparticle[i].x[j] = citycount;//粒子位置越界调整 让路径的每个点像速度一样变化取整else if (oldparticle[i].x[j] < 1) oldparticle[i].x[j] = 1;}//粒子位置有效性调整,必须满足解空间的条件Adjuxt_validParticle(oldparticle[i]);//对重复的城市去重oldparticle[i].fitness = Evaluate(oldparticle[i].x);//计算当前粒子的代价pbest[i].fitness = Evaluate(pbest[i].x);if (oldparticle[i].fitness < pbest[i].fitness)//如果当前粒子的代价比之前历史中粒子的代价都小,则替换为历史最小代价{for (int j = 0; j < citycount; j++)pbest[i].x[j] = oldparticle[i].x[j];}//更新单个粒子的历史极值for (int j = 0; j < citycount; j++)gbest.x[j] = pbest[i].x[j];//更新全局极值for (int k = 0; k < popsize && k != i; k++)//30 从单个最优中找一个全局最优保存起来{if (Evaluate(pbest[k].x) < Evaluate(gbest.x)){for (int j = 0; j < citycount; j++)gbest.x[j] = pbest[k].x[j];gbest.fitness = Evaluate(gbest.x);}}}//迭代30次outfile << "第" << ite + 1 << "次迭代后的种群如下:" << endl;for (int i = 0; i < popsize; i++){outfile << "粒子" << i + 1 << "->";for (int j = 0; j < citycount; j++){if (j == citycount - 1)outfile << oldparticle[i].x[j] << ") = " << oldparticle[i].fitness << endl;else if (j == 0)outfile << "f(" << oldparticle[i].x[j] << ",";elseoutfile << oldparticle[i].x[j] << ",";}}std::cout << "第" << ite + 1 << "次迭代后的最好粒子:";outfile << "第" << ite + 1 << "次迭代后的最好粒子:" << endl;for (int j = 0; j < citycount; j++){if (j == citycount - 1)outfile << gbest.x[j] << ") = " << gbest.fitness << endl;else if (j == 0)outfile << "f(" << gbest.x[j] << ",";elseoutfile << gbest.x[j] << ",";}gbest.shuchu();//每次迭代的全局最优}outfile.close();}
};int main()
{PSO pso;std::cout << "粒子群优化算法求解TSP旅行商问题" << endl;pso.PSO_TSP(30, 500, 2, 2, 0.8, 3.0, "data.txt");system("pause");return 0;
}
相关文章:

C++下基于粒子群算法解决TSP问题
粒子群优化算法求解TSP旅行商问题C(2020.11.12)_jing_zhong的博客-CSDN博客 混合粒子群算法(PSO):C实现TSP问题 - 知乎 (zhihu.com) 一、原理 又是一个猜答案的算法,和遗传算法比较像,也是设…...

vue3 ElementUI Switch before-change自动调用问题
使用 :beforeChange 这个属性 但是这个属性不能直接传值 如果直接传值依然会自动调用,需要使用自执行函数来****传值 解决 <el-switchv-model"rows[index].ifInjection":before-change"() > beforeChange(row)"/> :before-change"() > b…...
【chromium】windows 获取源码到本地
从github的chromium 镜像git clone 到2.5G失败了官方说不能,要去 windows_build_instructions vs2017和19都是32位的 vs2022是x64的 vs2022_install You may also have to set variable vs2022_install to your installation path of Visual Studio 2022,...

Nacos-Go-Sdk代码逻辑解析
文章目录 初始化服务,获取nacosClient获取配置源码逻辑 获取json配置发布配置监听配置变化源码逻辑listenConfigExecutor调度longPullinglongPullingcallListener监听表 中 配置 的 结构 监听功能的调用逻辑 初始化服务,获取nacosClient Nacos Client Co…...

检测opencv是否安装成功
winr打开命令提示符窗口: 输入 : python,进入python模块; 然后输入 import cv2出现>>>就代表opencv安装成功了; 同样的,也可以检测numpy等是否安装成功 最后输入 : exit() 退出python模块...

如果你是独立开发者,你是先写前端还是先写后端?
当我们站在独立开发的路口时,一个重要的抉择就摆在了我们面前:是先着手前端开发还是后端开发?这看似简单的问题,却蕴含着许多深刻的考虑和决策。无论你是准备构建一个复杂的分布式系统还是一个引人入胜的用户界面,接下…...
 Language Model (RNN-LM))
Pytorch intermediate(四) Language Model (RNN-LM)
前一篇中介绍了一种双向的递归神经网络,将数据进行正序输入和倒序输入,兼顾向前的语义以及向后的语义,从而达到更好的分类效果。 之前的两篇使用递归神经网络做的是分类,可以发现做分类时我们不需要使用时序输入过程中产生的输出&…...
C++零碎记录(十)
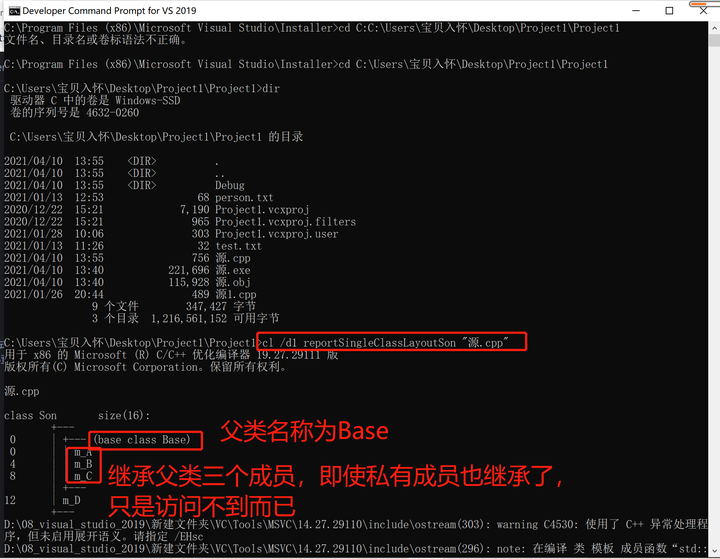
17. 继承对象内存 17.1 查询继承对象所占内存 #include <iostream> using namespace std; #include<string>//继承中的对象模型class Base { public:int m_A; protected:int m_B; private:int m_C; };//公共继承 class Son:public Base {int m_D; };//利用开发人…...

人类学习 vs. 机器学习
摘要: 机器学习与人类学习的范式有一定的联系. 本文发掘这些联系, 作用是指导人类的学习. 1. 什么是学习? 对于人类而言, 学习是改造大脑皮层的过程. 我们会发现, 不同人学习不同东西的能力也不一样, 如有些人数学厉害, 有些人音乐厉害. 同时, 也有些牛人, 学习到了学习的方…...
【LeetCode-中等题】15. 三数之和
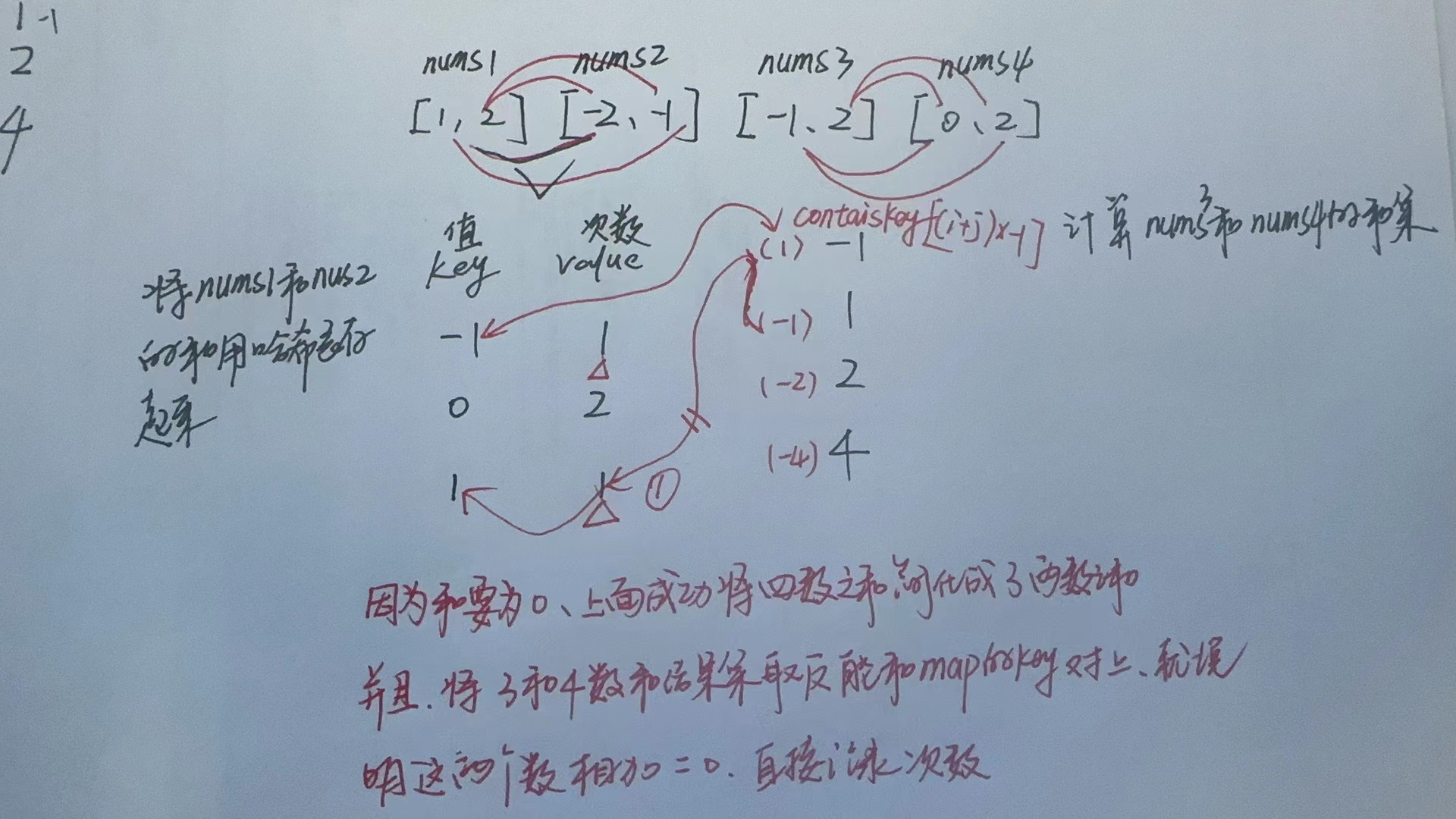
文章目录 题目方法一:哈希表 题目 方法一:哈希表 将四数之和 借助哈希表简化成两数之和 class Solution {public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {int res 0; //结果集数量Map<Integer,Integer> map n…...
Apache Tomcat漏洞复现
文章目录 弱口令启动环境漏洞复现 本地文件包含启动环境漏洞复现 弱口令 启动环境 来到vulhub/tomcat/tomcat8/靶场 cd vulhub/tomcat/tomcat8/安装环境并启动: sudo docker-compose up -d && sudo docker-compose up -d修改端口后启动: su…...
C++模版基础
代码地址 gitgithub.com:CHENLitterWhite/CPPWheel.git 专栏介绍 本专栏会持续更新关于STL中的一些概念,会先带大家补充一些基本的概念,再慢慢去阅读STL源码中的需要用到的一些思想,有了一些基础之后,再手写一些STL代码。 (如果你…...

解决 Elasticsearch 分页查询记录超过10000时异常
查询结果中 hits.total.value 值最大为10000的限制 解决方法: 1、请求设置rest_total_hits_as_inttrue 注意参数需要放在请求头上 builder.addHeader("rest_total_hits_as_int","true"); 2、修改setting的值 #设置返回最大记录条数为1000000 PUT /in…...
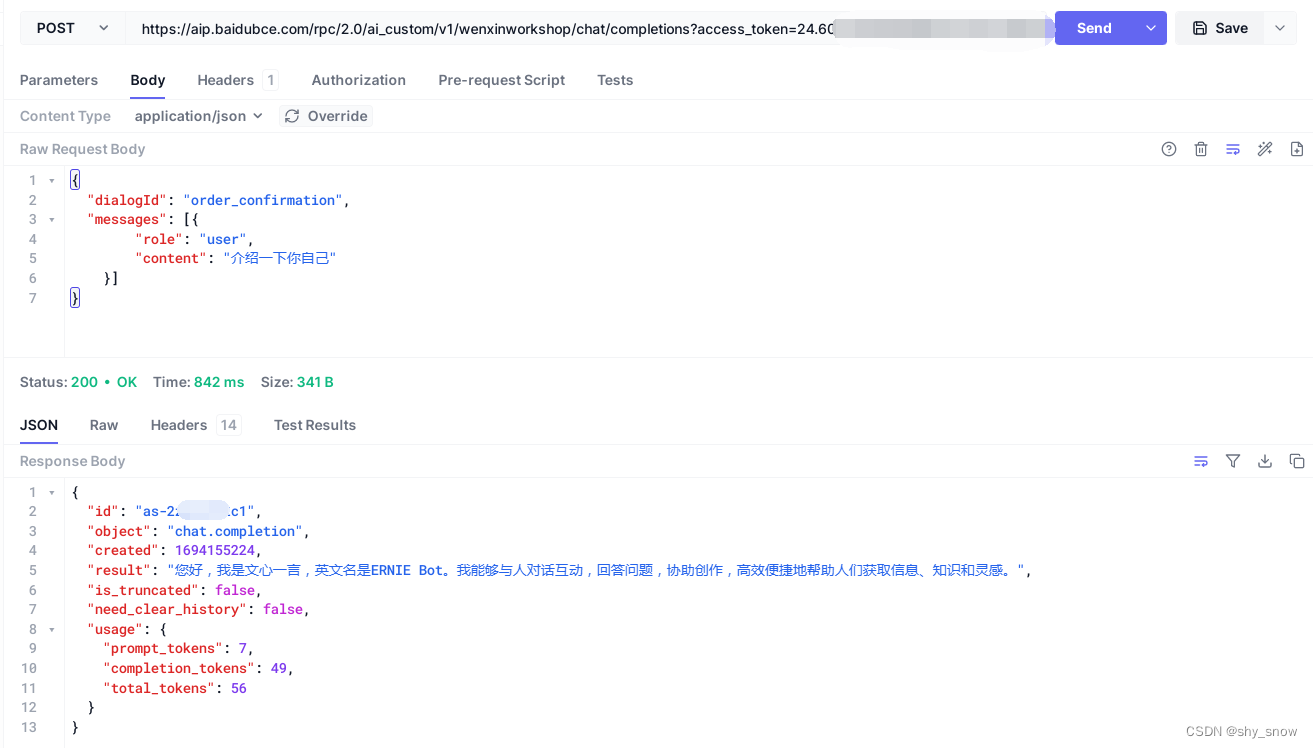
百度千帆大模型文心一言api调用
注册百度智能云账号并申请文心千帆大模型资格 https://login.bce.baidu.com/ https://cloud.baidu.com/product/wenxinworkshop 创建应用用于获取access_token 创建应用成功后,可以获取到API Key和Secret Key 获取access_token curl https://aip.baidubce.com/oauth/2.0/to…...
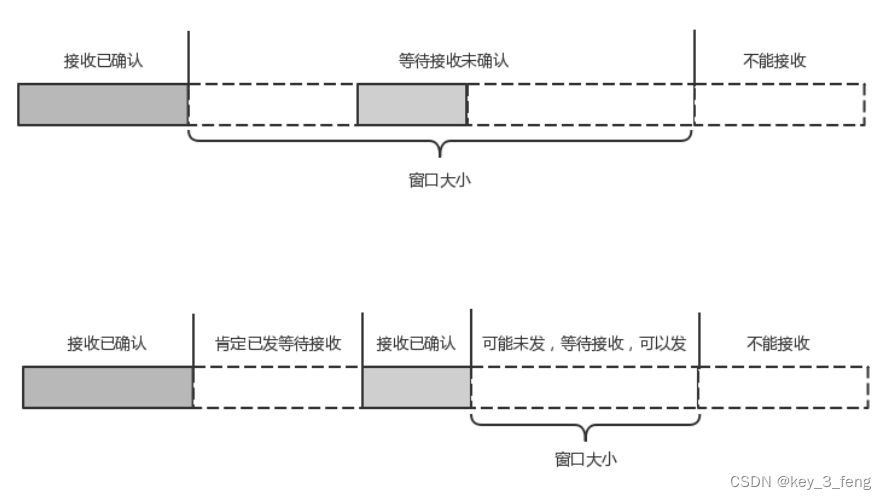
关于HTTP协议的概述
HTTP 的报文大概分为三大部分。第一部分是请求行,第二部分是请求的首部,第三部分才是请求的正文实体。 POST 往往是用来创建一个资源的,而 PUT 往往是用来修改一个资源的。 Accept-Charset,表示客户端可以接受的字符集。防止传过…...

ATFX汇市:8月名义与核心CPI走势分化,美国通胀率算升高还是降低?
ATFX汇市:据美国劳工部昨日公布的数据,8月份,美国名义CPI增速最新值3.7%,高于前值3.2%,高于预期值3.6%,显示高通胀问题有抬头迹象。同一时间公布的8月核心CPI年率最新值4.3%,低于前值4.7%&#…...

c++ 中的函数指针
以下图片演示了c中函数指针的用法。如下图可见,把函数地址赋值给函数指针,用函数名或者函数名的地址,都可以,c编译器不报错。即 ptr f 和 ptr &f 都对。但准确的话,函数名就是地址,在编译时候&#x…...

奶牛个体识别 奶牛身份识别
融合YOLOv5s与通道剪枝算法的奶牛轻量化个体识别方法 Light-weight recognition network for dairy cows based on the fusion of YOLOv5s and channel pruning algorithm 论文链接 知网链接 DOI链接 该文章讨论了奶牛花斑、光照条件、不同剪枝方法、不同剪枝率对准确率的影响…...
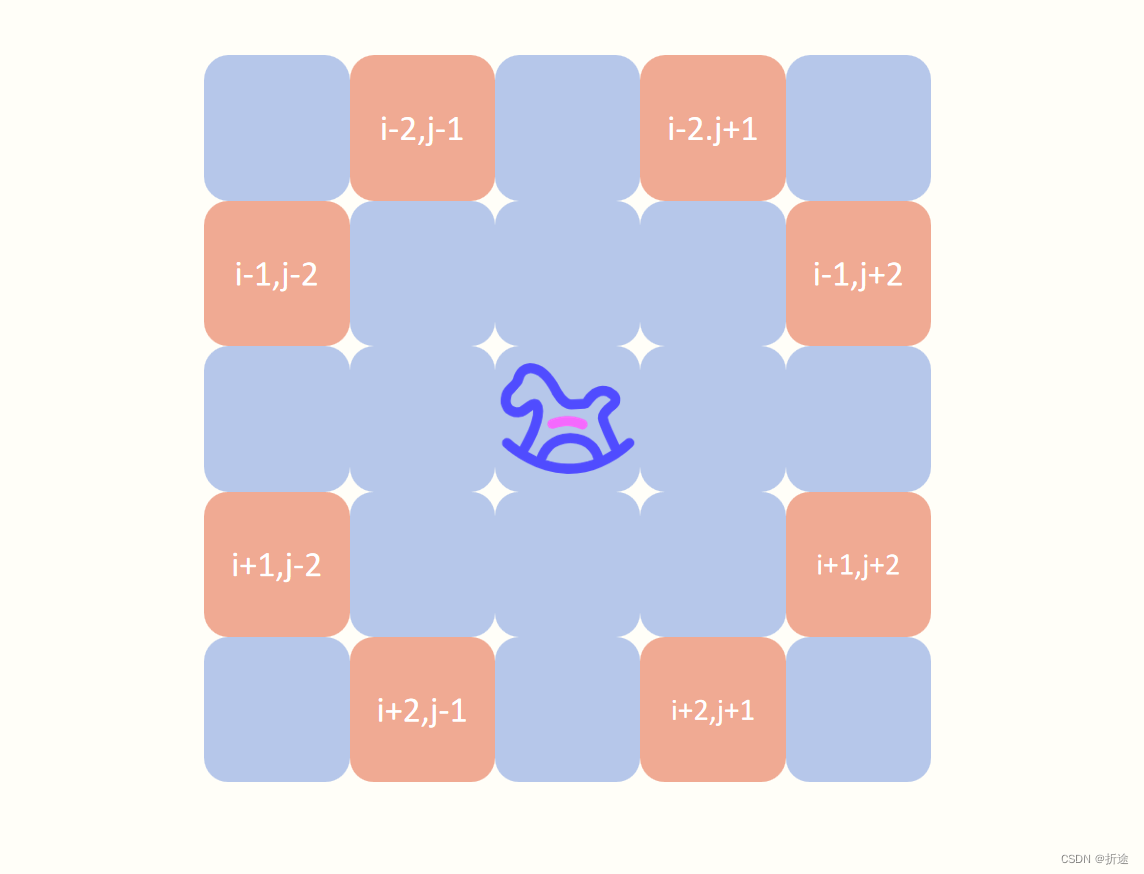
【力扣每日一题】2023.9.13 检查骑士巡视方案
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 题目给我们一个n*n大小的矩阵,矩阵的元素表示骑士已经行动的次数,问我们骑士能不能按照矩阵里元素顺序来巡视整个…...

【Vue】关于CSS样式绑定整理
因突发奇想设计一款组件,需要根据属性动态绑定样式,故而整理一些Vue的动态绑定样式方法(传参绑定类似,不做过多叙述),仅供参考.方式一: 直接在元素上绑定具体样式方式二: 定义属性对象,绑定到style,可以在style中使用定义的变量方式二: 通过引入自定义组件引入style数据,直接绑…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...
