为何红黑树在B/B+树之上仍然占据重要地位?
为何红黑树在B/B+树之上仍然占据重要地位?
- 引言
- 二、红黑树和B/B+树的基本原理
- 2.1、红黑树的特点和性质
- 2.2、B/B+树的特点和性质
- 2.3、红黑树和B/B+树的比较
- 三、B/B+树相对于红黑树的优势
- 四、红黑树仍然占据重要地位的原因
- 总结
博主简介
💡一个热爱分享高性能服务器后台开发知识的博主,目标是通过理论与代码实践的结合,让世界上看似难以掌握的技术变得易于理解与掌握。技能涵盖了多个领域,包括C/C++、Linux、数据结构与算法、Nginx、MySQL、Redis、fastdfs、kafka、Docker、TCP/IP、协程、DPDK等。
👉
🎖️ CSDN实力新星、CSDN博客专家、华为云云享专家、阿里云专家博主
👉
引言
红黑树是一种具有平衡性质的二叉搜索树,它通过将节点着色为红色或黑色,并通过一组特定的规则来保持树的平衡。
- 每个结点是红的或者黑的。
- 根结点是黑的。
- 每个叶子结点是黑的。
- 如果一个结点是红的,则它的两个儿子都是黑的。
- 对每个结点,从该结点到其子孙结点的所有路径上的 包含相同数目的黑结点 。
红黑树的平衡性能能够保证在最坏情况下的操作(插入、删除、查找)时间复杂度为O(log n)。
B/B+树是一种多路搜索树,主要用于在磁盘或其他多级存储介质上组织和管理大规模数据。一颗M阶B树T,满足以下条件:
- 每个结点至多拥有M颗子树。
- 根结点至少拥有两颗子树。
- 除了根结点以外,其余每个分支结点至少拥有M/2课子树。
- 所有的叶结点都在同一层上。
- 有k课子树的分支结点则存在k-1个关键字,关键字按照递增顺序进行排序。
- 关键字数量满足ceil(M/2)-1 <= n <= M-1。
B/B+树的平衡特性使得在大规模数据的增删改查操作中,其磁盘IO次数相对较少,能够提供更高的效率。
红黑树在数据结构中占据重要地位的原因包括其平衡性能、适用于索引结构、广泛应用于算法和数据处理,以及相对简单的实现方式。
- 红黑树在最坏情况下,红黑树的插入、删除和查找操作的时间复杂度都是O(log n)。
- 红黑树在算法和数据处理中广泛应用。例如,在图算法中,红黑树被用于存储顶点和边的关系,3. 以快速搜索和遍历图结构。
- 相对于其他平衡二叉搜索树数据结构,红黑树的实现方式相对简单。
二、红黑树和B/B+树的基本原理
2.1、红黑树的特点和性质
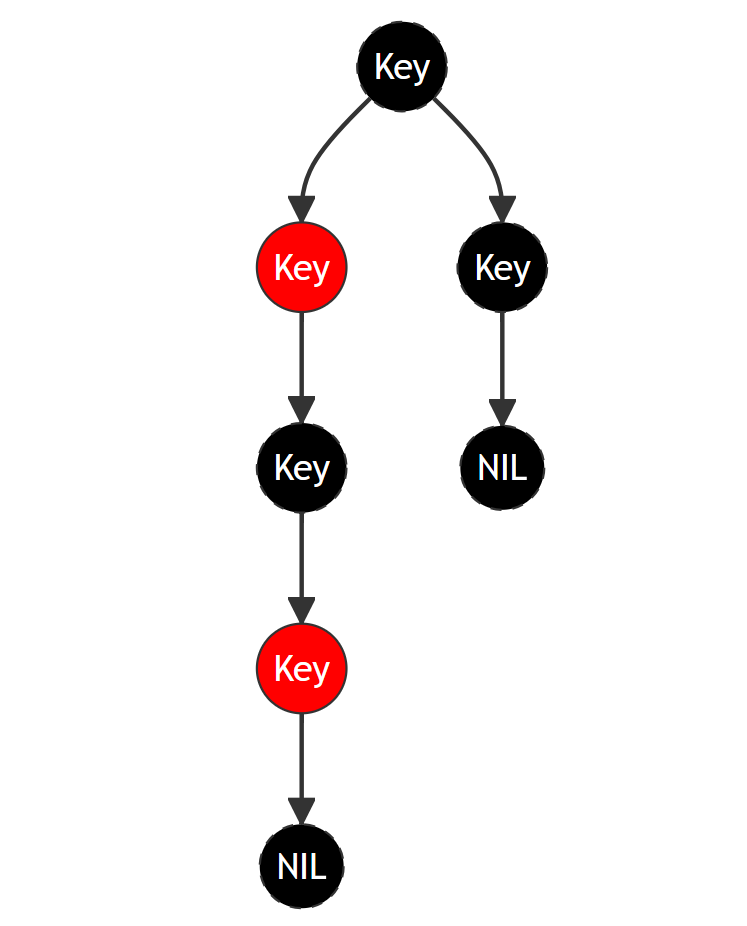
红黑树在二叉树的基础上具备如下的性质:
- 每个结点是红的或者黑的。
- 根结点是黑的。
- 每个叶子结点是黑的。
- 如果一个结点是红的,则它的两个儿子都是黑的。
- 对每个结点,从该结点到其子孙结点的所有路径上的 包含相同数目的黑结点 。
满足以上性质的二叉树就是红黑树。其中第五条性质就决定了红黑树的平衡,它不像AVL树那样严格要求两边子树的高度差是1,而是要求黑色节点的高度一致即可。
从第四条和第五条的性质中,我们可以总结出一个数学结论:红黑树的根节点到叶子节点的最短路径与红黑树的根节点到叶子节点的最长路径之比是 1 : ( 2 × N − 1 ) 1: (2\times N - 1) 1:(2×N−1)。
2.2、B/B+树的特点和性质
对上面的六个性质进行精简描述一下:
- 树开叉的数量上限是M颗,也就是定义了范围。
- 形容M颗子树与Key值的关系。
- 所有的叶子节点在同一层。
- 除了根节点以外,每个节点最少有 M ÷ 2 M \div 2 M÷2 颗子树。
在这里再扩展一些知识:
- B-tree / B tree:这种名称定义都是说的B树,不存在B"减"树这个数据结构。
- B+tree:B树的所有节点都是存储数据的,B+树是B树的扩展或者变种,B+树的内节点不存储数据,只做索引,所有的数据都存储在叶子节点。此外,B+树适合范围查阅是由链表性质决定的。
- B+树更适合做磁盘索引,性能优于B树;因为B+树的内结点不存储数据。同样的内存空间,B树的结点除了要存储key值,还要存储value值,所以B树的节点会比B+树的节点内存占用大,从而存储B树的节点会少于B+树的节点。
B树和B+树在使用场景上的差异说明:举个例子,假设有一个很大量的数据需要存储(比如100万个节点),内存上肯定无法全部存储,必然有很大部分在磁盘上。
-
如果使用B树进行存储,由于每个节点都存储数据,必然有一部分节点存储在内存中,一部分节点存储在磁盘上。
-
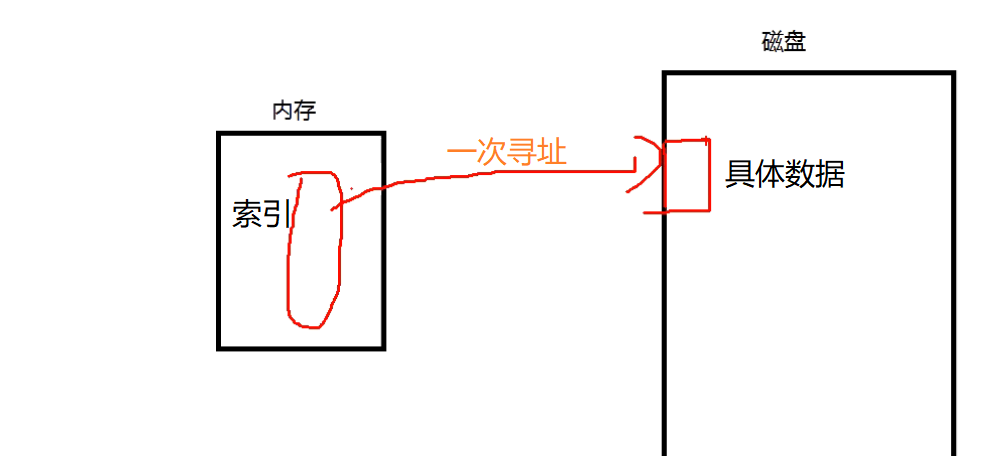
如果使用B+树存储,就有些不一样,由于B+树的内节点不存储具体数据,只做索引,所以B+树存储在内存中的节点数量会比B树多得多。所以,B+树做索引会更好,因为可以把所有的索引关系存储到内存中,然后通过一次性寻址找到存储具体数据的叶子节点。B树就无法做到这样,它只能一个节点一个节点的磁盘寻址。
B树和B+树都可以做索引,但是B+树更常用于做索引,特别是索引磁盘数据。比如MySQL、mongodb、PostgreSql等数据库的索引使用的就是B+树。
2.3、红黑树和B/B+树的比较
红黑树对于范围查询操作不如B/B+树高效。在红黑树中,需要进行中序遍历才能获取范围内的键值。B/B+树内部节点通过键值范围进行连接,因此在范围查询时,只需遍历相应的叶子节点链表即可,效率更高。
红黑树适用于内存中的高效搜索和平衡需求,而B/B+树适用于大规模数据的组织和管理,特别是在磁盘或其他多级存储介质中。
三、B/B+树相对于红黑树的优势
B/B+树在存储效率、范围查询效率、磁盘I/O优化、顺序访问性能以及分裂和合并操作效率等方面具有优势。这使得B/B+树成为在磁盘或其他多级存储介质上管理和组织大规模数据的一种重要的数据结构。
- B/B+树的节点可以存储多个键和对应的值,相比红黑树,每个节点能够容纳更多的数据。这样就减少了节点的数量,降低了存储空间的开销。
- B/B+树的内部节点通过键值范围进行连接,并且叶子节点通过链表连接在一起。这种结构的特点使得范围查询操作非常高效。只需遍历相应的叶子节点链表,而不需要像红黑树一样对整棵树进行中序遍历。
- B/B+树常用于在磁盘或其他多级存储介质上组织和管理大规模数据。B/B+树的分层结构使得在查找数据时只需进行少量的磁盘I/O操作,大大提高了访问速度。
- B/B+树中的键是按顺序存储的,这使得对数据的顺序访问效率非常高。对于需要顺序访问或顺序扫描大量数据的场景,B/B+树是一个很好的选择。
四、红黑树仍然占据重要地位的原因
- 在最坏情况下,红黑树的插入、删除和查找操作的时间复杂度都是O(log n),对于需要快速的搜索和排序操作的场景非常重要。
- 许多重要的数据结构和算法都是基于红黑树实现的,包括数据库系统、文件系统、编译器、图算法等。
- 红黑树的实现比较简单。
- 红黑树的性质非常稳定,插入和删除操作不会频繁地改变整棵树的结构。
- 红黑树经过了充分验证和优化,已存在许多成熟的实现和优化方案。
总结
尽管红黑树可能导致树的高度相对较高,但其存储效率、数据局部性、平衡性能和范围查询效率等特点在内存中或需要更好的数据局部性时,红黑树更好。
- 相比B树或B+树,红黑树的节点结构相对简单,每个节点只需额外存储一个颜色位。
- 红黑树在插入和删除操作时能够通过旋转和重新着色来保持平衡性质。相比之下,B树或B+树的平衡调整操作(如节点的分裂和合并)可能更复杂。

相关文章:

为何红黑树在B/B+树之上仍然占据重要地位?
为何红黑树在B/B树之上仍然占据重要地位? 引言二、红黑树和B/B树的基本原理2.1、红黑树的特点和性质2.2、B/B树的特点和性质2.3、红黑树和B/B树的比较 三、B/B树相对于红黑树的优势四、红黑树仍然占据重要地位的原因总结 博主简介 💡一个热爱分享高性能服…...

【算法专题突破】滑动窗口 - 水果成篮(13)
目录 1. 题目解析 2. 算法原理 3. 代码编写 写在最后: 1. 题目解析 题目链接:904. 水果成篮 - 力扣(Leetcode) 题目有很长一段话,但是我们读一遍题目可以提炼转化出题目的要求 : 其实就是找出一个最长…...

Peppercontent.io:人工智能驱动的内容生成工具
【产品介绍】 名称 Peppercontent.io 成立时间 成立于2017年 具体描述 Peppertype.ai 是一种基于GPT-3的AI辅助工具,而GPT-3则是一种深度学习自回归语言模型。这一技术潜藏着巨大的潜力,可以立刻为企业和创作者提供创意内容&…...

docker镜像管理-实操
一.docker镜像管理 1.拉取镜像 docker image pull <repository>:<tag> 镜像名称和标签使用 : 进行分隔,如果省略了标签,则默认为 latest docker image pull nginx:latest 或者docker pull nginx:latest 拉取下来的镜像默认保存在࿱…...
SpringMVC-----JSR303以及拦截器
目录 JSR303 什么是JSR303 JSR303的作用 JSR303常用注解 入门使用 拦截器是什么 拦截器的工作原理 拦截器的作用 拦截器的使用 JSR303 什么是JSR303 JSR303是Java为Bean数据合法性校验提供给的标准框架,已经包含在JavaEE6.0中1。 JSR303通过在Bean属性中标…...
基于若依框架实现markdown在线编辑
基于若依框架实现markdown在线编辑 1. 下载mavon-editor npm install mavon-editor --save2. 打开main.js文件, 添加如下 // markdown组件 import { mavonEditor } from "mavon-editor"; import "mavon-editor/dist/css/index.css";// markdown组件 Vue…...

CentOS7上从0开始搭建Zookeeper集群
CentOS7上搭建Zookeeper集群 环境准备安装jdk安装zookeeper下载zookeeper解压zookeeper修改zookeeper配置文件 搭建zookeeper集群修改zoo.cfg文件添加myid文件启动zookeeper集群 环境准备 首先你需要准备三台zookeeper(待会会讲zookeeper的安装流程)&am…...
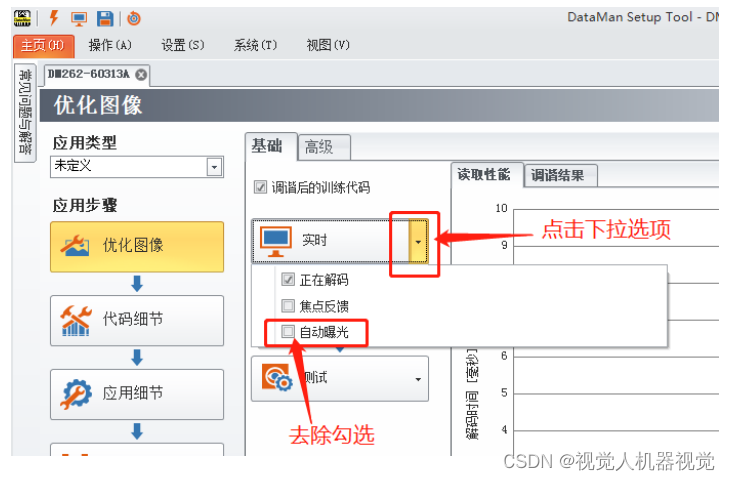
康耐视读码器DataMan软件详细使用步骤
1、 点击桌面已经安装好的 dataman 软件并打开 2、 打开之后,点击刷新,刷出来读码器的图标,双击进行连接,或者选中后,点击右下角 的连接。(也可先进行第 9—(2)步更改读码器的 IP,对应的连接对象也更改到同一网 段)如图 3、 连接之后,在设置 快速设置下面把实时显…...

408强化(番外)文件管理
有点看不下去书,408,哎好久没看了,死磕数学时完全不想看其他科目,数学分数也尚未质变。 突然想到一个好点子,只看大纲尝试回忆一下这章的内容。 文件就是为了方便用户使用,按名访问而提出的,从…...

iptables 防火墙配置
文章目录 iptables 防火墙配置规则链的分类–五链处理的动作iptables 常用参数和作用iptables 防火墙配置查看规则链清空规则链设置默认规则将流入的流量丢弃允许ICMP协议流量通过删除默认策略允许所以流量通过设置将所有流入22端口的流量全部拒绝允许指定网段的22端口通过设置…...

面试官:我们深入聊聊Java虚拟机吧
哈喽!大家好,我是奇哥,一位专门给面试官添堵的职业面试员 文章持续更新,可以微信搜索【小奇JAVA面试】第一时间阅读,回复【资料】更有我为大家准备的福利哟! 文章目录 前言面试Java虚拟机内存模型垃圾收集器…...
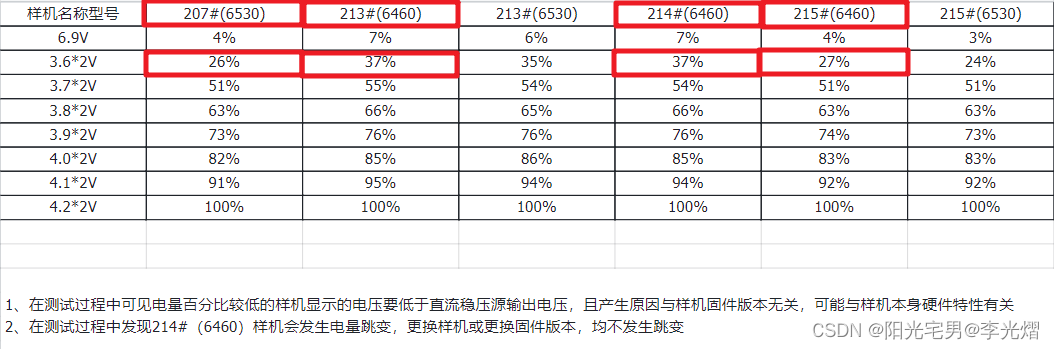
【电源专题】案例:异常样机为什么只在40%以下电量时与其他样机显示电量差异10%,40%以上电量差异却都在5%以内。
本案例发生在一个量产产品的测试中,因为产品带电池,所以需要测试产品对于电池电量显示的精确程度。产品使用的是最简单的开路电压查表法进行设计。 案例测试报告的问题在于不同样机之间电量百分比存在差异,大部分是在3%~4%之间。但在7.2V电压时,能够差异10%左右。 在文章:…...
React 全栈体系(七)
第四章 React ajax 一、理解 1. 前置说明 React本身只关注于界面, 并不包含发送ajax请求的代码前端应用需要通过ajax请求与后台进行交互(json数据)react应用中需要集成第三方ajax库(或自己封装) 2. 常用的ajax请求库 jQuery: 比较重, 如果需要另外引入不建议使用axios: 轻…...

NVIDIA 显卡硬件支持的精度模式
很多炼丹师不知道自己英伟达显卡支持哪些精度模式,本文整理了NVIDIA官网的数据,为你解开疑惑。 1. 首先了解CUDA计算能力及其支持的精度模式; 2. 查看自己显卡(或其它NVIDIA硬件)的计算能力值为多少。 表1 CUDA计算…...

【Java|golang】210. 课程表 II---拓扑排序
一、拓扑排序的定义: 先引用一段百度百科上对于拓扑排序的定义: 对一个有向无环图 ( Directed Acyclic Graph 简称 DAG ) G 进行拓扑排序,是将 G 中所有顶点排成一个线性序列,使得图中任意一对顶点 u 和 v ,若边 <…...

STM32CubeMX systick bug?
发觉用新版(V6.9.1)的它生成代码,会有问题。可能是 BUG。具体如下: 一个简单的点灯程序,用 Keil MDK 5.38a(compiler version 6)编译。 如果在变量前,不加上关键字“volatile”&am…...

徐亦达机器学习:Kalman Filter 卡尔曼滤波笔记 (一)
P ( x t P(x_t P(xt| x t − 1 ) x_{t-1}) xt−1) P ( y t P(y_t P(yt| x t ) x_t) xt) P ( x 1 ) P(x_1) P(x1)Discrete State DM A X t − 1 , X t A_{X_{t-1},X_t} AXt−1,XtAny π \pi πLinear Gassian Kalman DM N ( A X t − 1 B , Q ) N(AX_{t-1}B,Q)…...

Java和vue的包含数组组件contains、includes
List<String> tempList Arrays.asList("10018","1007","10017","1012"); if(tempList.contains(initMap.get("asset_type_id").toString())){// todo 计算运营终点桩号-起点桩号BigDecimal diffSum collectNum(col…...
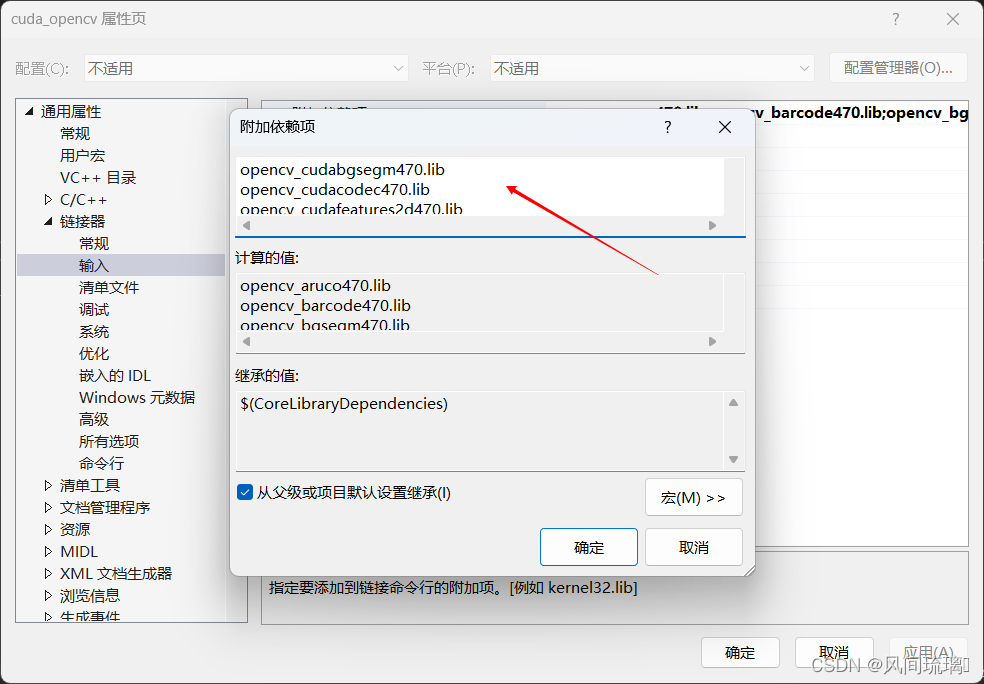
OpenCV_CUDA_VS编译安装
一、OpenCV 我这里是下载的OpenCV4.5.4,但是不知道到在vs里面build时一直报错,后面换了4.7.0的版本测试,安装成功。 Release OpenCV 4.5.4 opencv/opencv GitHub 这个里面有官方预编译好的OpenCV库,可以直接食用。 扩展包&am…...
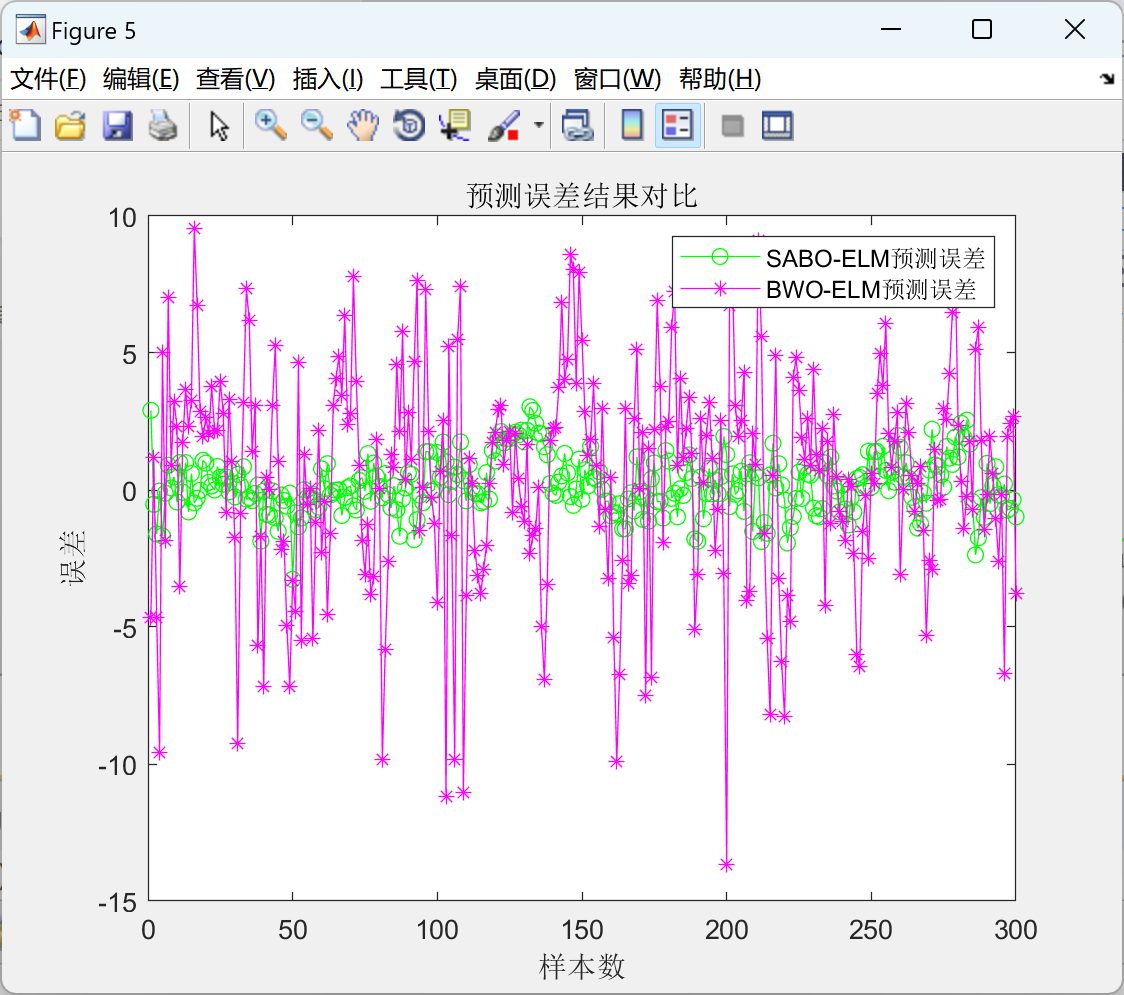
基于减法优化SABO优化ELM(SABO-ELM)负荷预测(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...
