数据分享|R语言武汉流动人口趋势预测:灰色模型GM(1,1)、ARIMA时间序列、logistic逻辑回归模型...
全文链接:http://tecdat.cn/?p=32496
人口流动与迁移,作为人类产生以来就存在的一种社会现象,伴随着人类文明的不断进步从未间断(点击文末“阅读原文”获取完整代码数据)。
相关视频
人力资源是社会文明进步、人民富裕幸福、国家繁荣昌盛的核心推动力量。当前,我国经济正处于从以政府主导的投资驱动型的经济“旧常态”向以市场需求为主导的经济“新常态”转型过渡期。
本文帮助客户综合运用R语言灰色预测模型和logistic逻辑回归模型,以及综合运用ARIMA模型和logistic模型,得到武汉市外省流入人口规模(查看文末了解数据免费获取方式)的预测。
文献回顾
国内关于流动人口的定量预测模型有很多,如马尔萨斯模型[1]、马尔可夫链模型[2]、指数平滑预测模型[3]、宋健模型、BP神经网络模型、单变量的双曲模型[4]、系统动力学模型、Leslie人口预测模型[5]、年龄移算法[6-8]以及CPPS 软件预测等。然而,在经济学和管理学范畴内﹐最为主要的有三种,分别是:
第一,灰色预测模型。1982年,我国学者邓聚龙教授创立了灰色系统理论﹐灰色系统理论的研究对象是“部分信息已知,部分信息未知”的“小样本”、“贫信息”不确定性系统。GM(1,1)模型是最常用的一种灰色模型,由一个只含单变量的一阶微分方程构成的模型。国内不少学者运用灰色预测模型对我国总人口规模的发展趋势进行预测[9-11]。还有一部分学者从区域发展的角度出发,构建了一系列城市人口或区域流动人口的灰色预测模型[12一14]。为了减少预测的误差,学者们进一步修正了GM(1,1)灰色预测模型,构建了“等维灰数递补动态预测”模型对人口进行定量预测[15] 。
第二,Logistic曲线模型。Logistic曲线呈S形,称为生长曲线。Logistic方程最早由比利时数学家P. F. Verhult于1838年提出。但长期埋没﹐直到20世纪20年代被生物学家与人口统计学家R.Pearl和L.J. Reed重新发现。经不断完善和发展,现广泛用于人口和商业分析中。我国学者多运用Logistic模型预测我国某地区的人口数量、流动人口规模等[16—20]
第三,时间序列模型。时间序列分析方法是伯克斯和詹金斯(Box-Jenkins)1976年提出的。
数据来源与处理
将武汉市外省流入人口的时间序列记为{Yt}。
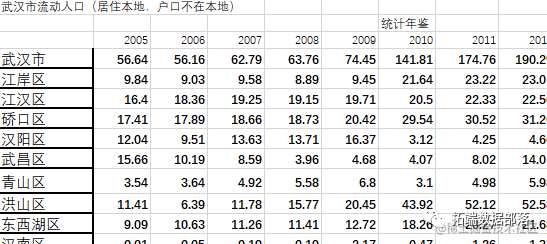
武汉市外来流入人口数据表
点击标题查阅往期内容
R语言用logistic逻辑回归和AFRIMA、ARIMA时间序列模型预测世界人口

左右滑动查看更多

01
02
03
04
ARIMA模型
为降低原始数据随机波动的影响,先要对原始数据进行平滑处理,本文采用常用的三点移动平均法。计算公式如下:
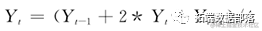
首端点数据进行移动平均时,Yt-1取Yt,末端点数据进行移动平均时,Yt+1取Yt。
另外,由于取对数,不会改变数据的性质和关系,且得到的数据易消除异方差。
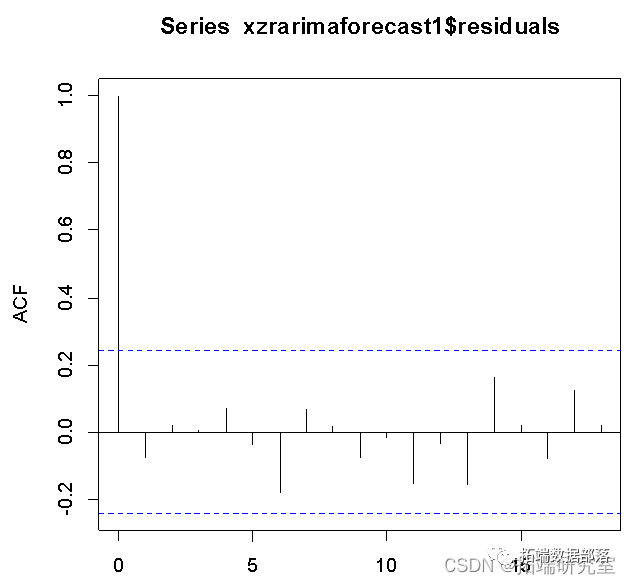
acf(dy)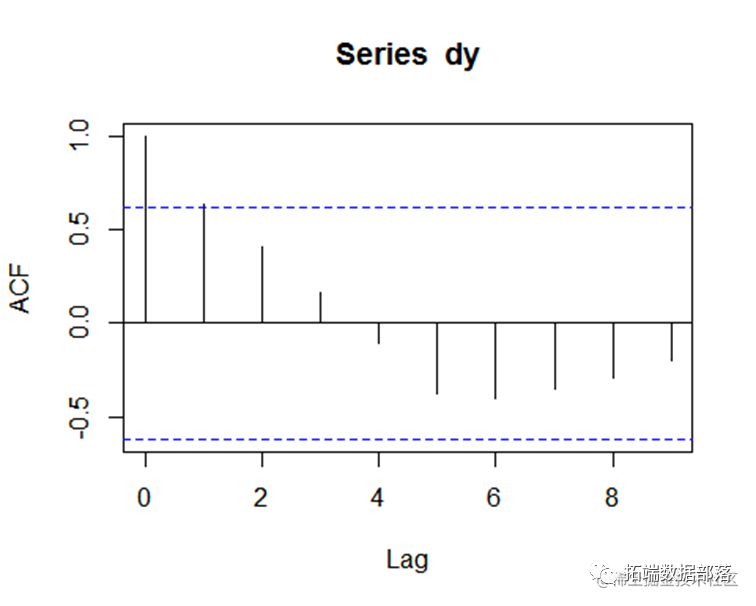
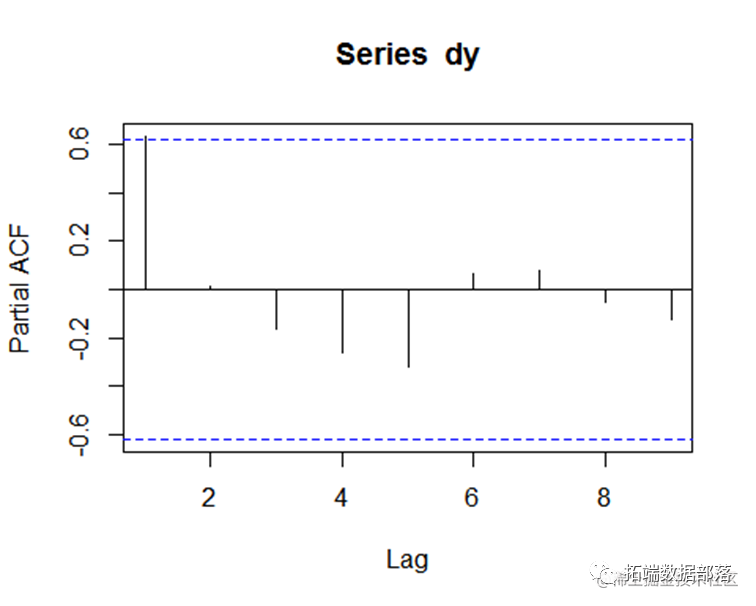
然后用自相关图检查序列的平稳性,最后发现一阶差分后的序列是平稳的。
下面对平稳性序列 建立 模型 ,偏相关系数在滞后1期后很快地趋向于0,所以取p=1 ,自相关系数图形具有拖尾性,所以初步判断为ar(1)模型。
参数估计
arima(dy,order=c(p,0,q) )
which.min(aiclist$AIC)尝试不同的p和q的值,得出最优AIC的模型。
从AIC的结果来看,arima(2,1,1)模型拥有最小的AIC值,因此为最优模型,因此将arima(2,1,1)模型作为最优模型。
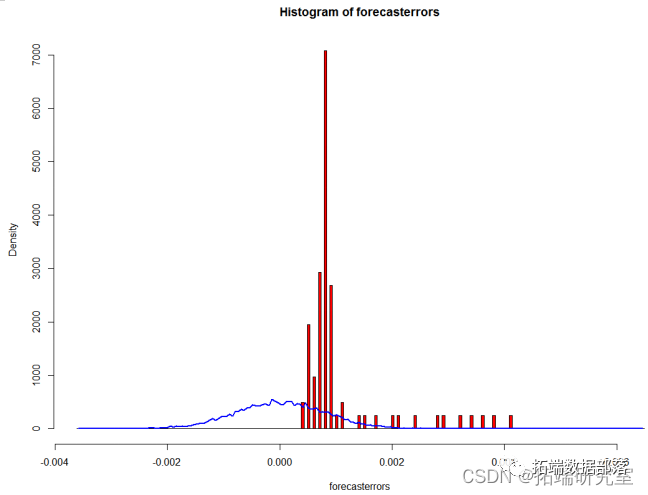
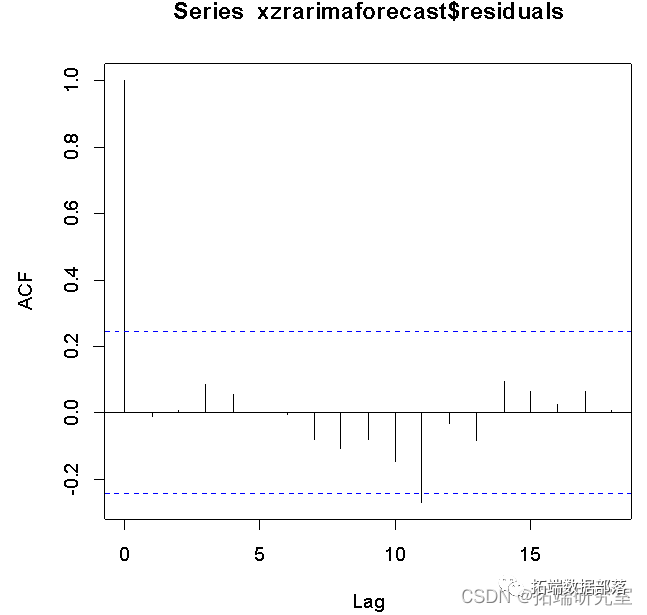
对残差序列进行白噪声检验,通常考虑残差序列的随机性,即用伯克斯.皮尔斯 提出的I统计量进行检验,用修正的I统计量:
Box.test(model$residuals,type="Ljung")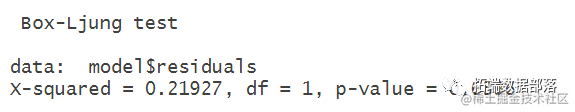
在这里X-squared的值就是0.21927,概率值为0.6396,说明拒绝原假设。
犯第一类错误的概率为0.6396,这说明残差序列相互独立即为白噪声序列的概率很大,故不能拒绝残差序列是一个白噪声序列,检验通过。
单位根平稳性检验 检验

建立arima模型进行比较

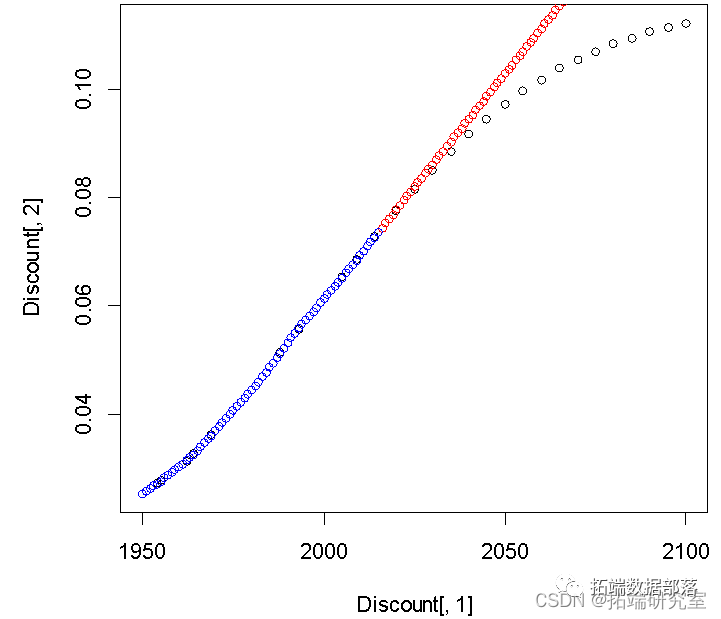
ARIMA模型预测
pred=predict(model, 15)$pred绘制预测序列时间图
plot( pred,type="b" ,main="ARIMA模型预测")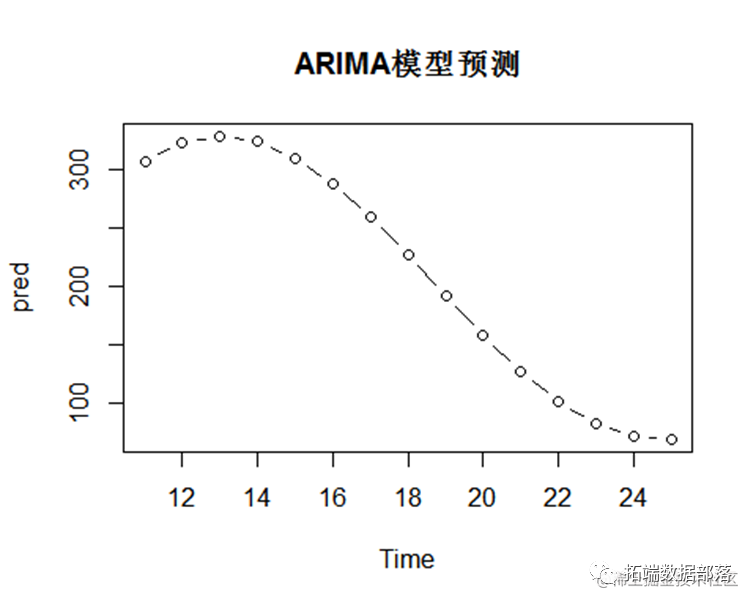
而arima模型预测的数据开始波动较大,到后面有逐渐平稳的趋势。
建立灰色模型GM(1,1)对应的函数
GM11<-function(x0,t,x){ #x0为输入训练数据序列列,t为预测个数,x为原始数据(训练数据+测试集) x1<-cumsum(x0) #一次累加生成序列1-AG0序列 b<-numeric(length(x0)-1) n<-length(x0)-1 for(i in 1:n){ #生成x1的紧邻均值生成序列 b[i]<--(x1[i]+x1[i+1])/2 b} #得序列b,即为x1的紧邻均值生成序列 D<-numeric(length(x0)-1) D[]<-1 B<-cbind(b,D) BT<-t(B)#做逆矩阵计算相对误差
e2<-numeric(length(x0)) for(s in 1:length(x0)){ e2[s]<-(abs(e[s])/x0[s]) #得相对误差 } cat("相对残差:",'\n',e2,'\n','\n') cat("残差平方和=",sum(e^2),'\n') cat("平均相对误差=",sum(e2)/(length(e2)-1)*100,"%",'\n') cat("相对精度=",(1-(sum(e2)/(length(e2)-1)))*100,"%",'\n','\n')后验差比值检验
avge<-mean(abs(e));esum<-sum((abs(e)-avge)^2);evar=esum/(length(e)-1);se=sqrt(evar) #计算残差的方差画出输入序列x0的预测序列及x0的比较图像
plot(xy,col='blue',type='b',pch=16,xlab='时间序列',ylab='值') points(x,col='red',type='b',pch=4)拟合模型
GM11(train,length(mynx),mynx)
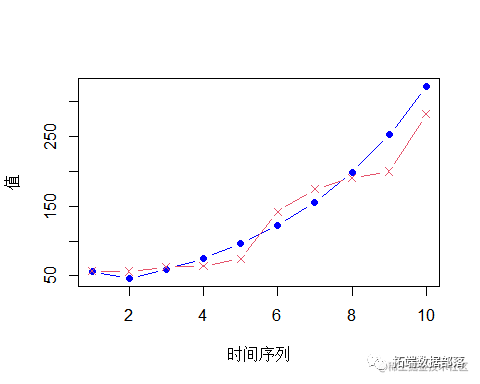
预测15年的人口数
GM11(train,length(myn
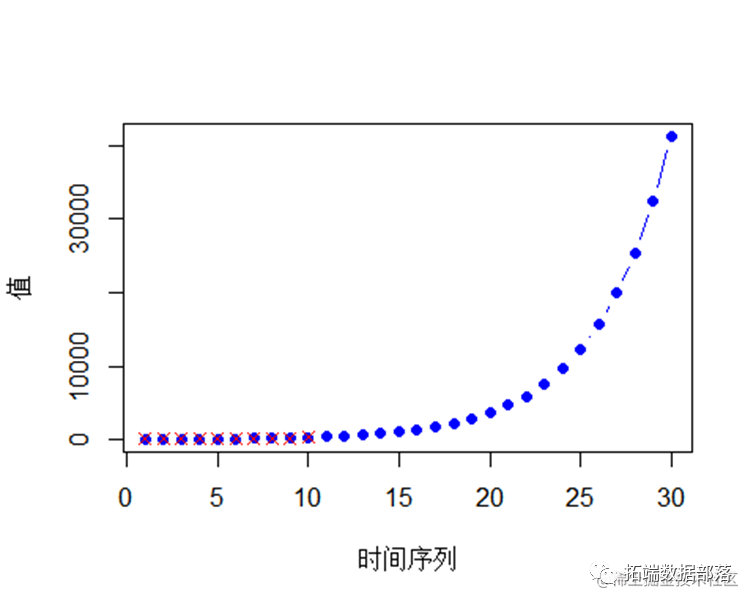
logistic逻辑回归模型
glm(as.numeric(yy[1:lengt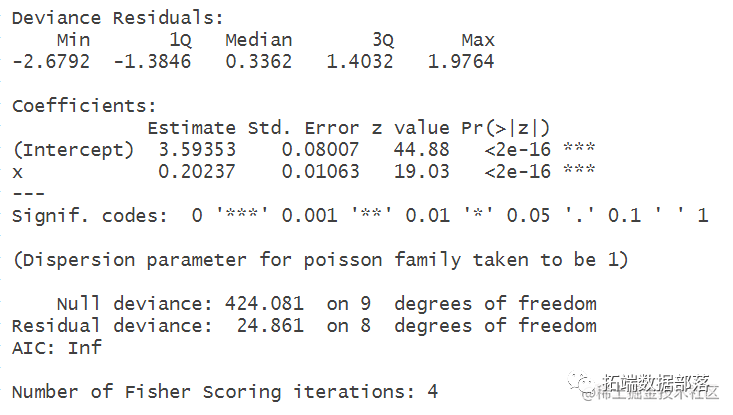
预测
predict(model,newd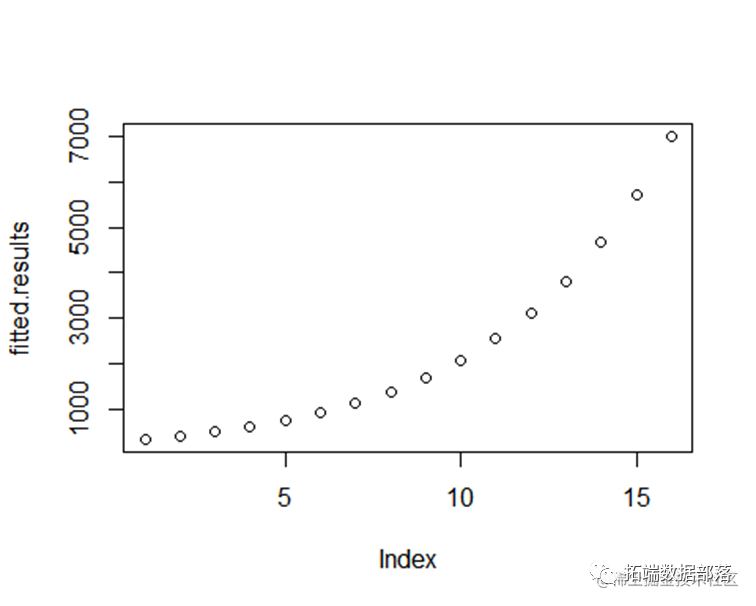
参考文献
[1]林泽楷,许梦瑶,陈以丙.人口预测模型的优化[J].科技致 富向导,2011(8):89-89.
[2]昝欣,宗鹏,吴祈宗.马尔可夫链在高校教师人才流动预测 中的应用[J].科技进步与对策,2007,24(1):185-187.
[3]涂雄苓,徐海云.ARlMA与指数平滑法在我国人口预测中的 比较研究[J].统计与决策,2009(16):21-23.
[4]杨辉.上海市流动人口发展趋势与预测[J].人口学刊,1995 (2):31-34.
[5]冯守平.中国人口发展预测模型的构建与应用[J].统计与 决策,2010(15):24-27.
[6]胡启迪,杨庆中,桂世勋,等.上海市区人口迁移预测模型的 研究[J].人口与经济,1986(1):17-22.
[7]周德禄.经济技术开发区人口变动预测实证研究———以青 岛经济技术开发区为例[J].东岳论丛,2006,27(5):60-63.
[8]路锦非,王桂新.我国未来城镇人口规模及人口结构变动预 测[J].西北人口,2010(4):1-6.
[9]郝永红,王学萌.灰色动态模型及其在人口预测中的应用 [J].数学的实践与认识,2002,32(5):813-820.
[10]周诗国.我国人口的灰色预测模型研究及其应用[J].数理 医药学杂志,2005,18(4):307-309.
[11]陈作清,李远平,吴霞,等.基于灰色预测的我国人口预测 模型分析[J].中南民族大学学报:自然科学版,2008,27 (1):111-114.
[12]周瑞平.GM(1,1)模型灰色预测法预测城市人口规模[J]. 内蒙古师范大学学报:自然科学版,2005,34(1):81-83.
[13]郑元世,张启敏.银川市人口的灰色预测[J].辽宁工学院 学报,2008,27(5):346-350.
[14]李群,董守义,孙立成,等.我国高层次人才发展预测与对 策[J].系统工程理论与实践,2008,28(2):125-130.
[15]李晓梅.城市流动人口预测模型探讨[J].南京人口管理干 部学院学报,2006,22(4):26-29.
[16]亓昕.北京未来流动人口预测方法探讨及发展趋势[J].人 口与经济,1999(3):52-56.
[17]武萍,陶静.沈阳市流动人口预测与分析[J].锦州师范学 院学报:自然科学版,2001,22(3):69-71.
[18]李振福.长春市城市人口的Logistic模型预测[J].吉林师 范大学学报:自然科学版,2003(1):16-19.
数据获取
在公众号后台回复“人口数据”,可免费获取完整数据。

本文中分析的数据分享到会员群,扫描下面二维码即可加群!

点击文末“阅读原文”
获取全文完整代码数据资料。
本文选自《R语言武汉流动人口趋势预测:灰色模型GM(1,1)、ARIMA时间序列、logistic逻辑回归模型》。


点击标题查阅往期内容
R语言时间序列:ARIMA / GARCH模型的交易策略在外汇市场预测应用
R语言中的时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格
R语言用Garch模型和回归模型对股票价格分析
R语言对S&P500股票指数进行ARIMA + GARCH交易策略
R语言ARMA GARCH COPULA模型拟合股票收益率时间序列和模拟可视化
ARMA-GARCH-COPULA模型和金融时间序列案例
时间序列分析:ARIMA GARCH模型分析股票价格数据
GJR-GARCH和GARCH波动率预测普尔指数时间序列和Mincer Zarnowitz回归、DM检验、JB检验
【视频】时间序列分析:ARIMA-ARCH / GARCH模型分析股票价格
时间序列GARCH模型分析股市波动率
PYTHON用GARCH、离散随机波动率模型DSV模拟估计股票收益时间序列与蒙特卡洛可视化
极值理论 EVT、POT超阈值、GARCH 模型分析股票指数VaR、条件CVaR:多元化投资组合预测风险测度分析
Garch波动率预测的区制转移交易策略
金融时间序列模型ARIMA 和GARCH 在股票市场预测应用
时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格
R语言风险价值:ARIMA,GARCH,Delta-normal法滚动估计VaR(Value at Risk)和回测分析股票数据
R语言GARCH建模常用软件包比较、拟合标准普尔SP 500指数波动率时间序列和预测可视化
Python金融时间序列模型ARIMA 和GARCH 在股票市场预测应用
MATLAB用GARCH模型对股票市场收益率时间序列波动的拟合与预测
R语言GARCH-DCC模型和DCC(MVT)建模估计
Python 用ARIMA、GARCH模型预测分析股票市场收益率时间序列
R语言中的时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格
R语言ARIMA-GARCH波动率模型预测股票市场苹果公司日收益率时间序列
Python使用GARCH,EGARCH,GJR-GARCH模型和蒙特卡洛模拟进行股价预测
R语言时间序列GARCH模型分析股市波动率
R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测
matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计
Python使用GARCH,EGARCH,GJR-GARCH模型和蒙特卡洛模拟进行股价预测
使用R语言对S&P500股票指数进行ARIMA + GARCH交易策略
R语言用多元ARMA,GARCH ,EWMA, ETS,随机波动率SV模型对金融时间序列数据建模
R语言股票市场指数:ARMA-GARCH模型和对数收益率数据探索性分析
R语言多元Copula GARCH 模型时间序列预测
R语言使用多元AR-GARCH模型衡量市场风险
R语言中的时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格
R语言用Garch模型和回归模型对股票价格分析
GARCH(1,1),MA以及历史模拟法的VaR比较
matlab估计arma garch 条件均值和方差模型
R语言POT超阈值模型和极值理论EVT分析

![]()

相关文章:

数据分享|R语言武汉流动人口趋势预测:灰色模型GM(1,1)、ARIMA时间序列、logistic逻辑回归模型...
全文链接:http://tecdat.cn/?p32496 人口流动与迁移,作为人类产生以来就存在的一种社会现象,伴随着人类文明的不断进步从未间断(点击文末“阅读原文”获取完整代码数据)。 相关视频 人力资源是社会文明进步、人民富裕…...
解决 Axios 跨域问题,轻松实现接口调用
跨域是指访问另外一个域的资源,由于浏览器的同源策略,默认情况下使用 XMLHttpRequest 和 Fetch 请求时是不允许跨域的。跨域的根本原因是浏览器的同源策略,这是由浏览器对 JavaScript 施加的安全限制。 Axios 跨域常见报错 跨域请求被阻止 (…...

Layui快速入门之第十节 表单
目录 一:基本用法 二:输入框 普通输入框 输入框点缀 前置和后置 前缀和后缀 动态点缀 密码显隐 内容清除 自定义动态点缀 点缀事件 三:复选框 默认风格 标签风格 开关风格 复选框事件 四:单选框 普通单选框 自…...
Linux之yum/git的使用
目录 一、yum 1、关于yum 2、yum的操作 ①、yum list ②、yum install ③、yum remove 二、git 1、Linux中连接gitee 2、git的操作 ①git add [文件] ②git commit -m "提交日志" ③git push 3、可能出现的问题 ①配置用户名、邮箱 ②出现提交冲突 ③…...

使用ExcelJS快速处理Node.js爬虫数据
什么是ExcelJS ExcelJS是一个用于处理Excel文件的JavaScript库。它可以让你使用JavaScript创建、读取和修改Excel文件。 以下是ExcelJS的一些主要特点: 支持xlsx、xlsm、xlsb、xls格式的Excel文件。可以创建和修改工作表、单元格、行和列。可以设置单元格样式、字…...
轻量级的Python IDE —— Thonny
现在的开发工具太多了,而且每个开发工具都致力于做成最好用最智能的工具,所以功能越堆越多,越怼越智能。安装这些开发工具比较烧脑,经常需要经过许多配置步骤。作为一个 Python 开发者来说,好多人光是这些配置都要弄半…...

java设计模式之观察者模式
. 基本概念 观察者(Observer)模式中包含两种对象,分别是目标对象和观察者对象。在目标对象和观察者对象间存在着一种一对多的对应关系,当这个目标对象的状态发生变化时,所有依赖于它的观察者对象都会得到通知并执行它…...

掌动智能分享:性能压力测试的重要性与优势
在当今数字化时代,应用程序的性能对于用户体验和业务成功至关重要。为了保证应用程序的高性能和稳定性,性能压力测试成为了不可或缺的环节。在这个领域,掌动智能作为一家专业的性能压力测试公司,正以其卓越的技术与服务࿰…...

C# ppt文件转换为pdf文件
使用第三方插件 Office 实现转换 1.Application方式转换 /// <summary>/// Microsoft.Office.Interop.PowerPoint/// 使用第三方软件 office/// </summary>/// <param name"pptPath">需要转换的ppt文件路径</param>/// <param name"…...
使用Pyarmor保护Python脚本不被反向工程
Python可读性强,使用广泛。虽然这种可读性有利于协作,但也增加了未授权访问和滥用的风险。如果未采取适当的保护,竞争对手或恶意攻击者可以复制您的算法和专有逻辑,这将对您软件的完整性和用户的信任产生负面影响。 实施可靠的安…...
STM32单片机——串口通信(轮询+中断)
STM32单片机——串口通信(轮询中断) 串口通信相关概念HAL库解析及CubeMX工程配置与程序设计常用函数介绍CubeMX工程配置HAL库程序设计(轮询中断)轮询数据收发中断收发数据 固件库程序设计及实现固件库配置流程结构体配置及初始化程…...

Python if语句的嵌套应用
视频版教程 Python3零基础7天入门实战视频教程 有时候业务上有多维度复杂条件判断,我们需要用到if语句的嵌套来实现。 举例:我们在一些游戏网站活动充值的时候,冲100送 20 冲200送50 但是vip用户的话,冲100送 30 冲200送70 代码…...

C++中带默认值的函数参数
C中带默认值的函数参数 如果一直将 Pi 声明为常量,没有给用户提供修改它的机会。然而,用户可能希望其精度更高或更低。如何编写一个函数,在用户没有提供的情况下,将 Pi 设置为默认值呢? 为解决这种问题,一…...

记录一次部署Hugo主题lotusdocs到Github Pages实践
引言 随着开源项目的越来越复杂,项目文档的重要性日渐突出。一个好的项目要有一个清晰明了的文档来帮助大家使用。最近一直有在找寻一个简洁明了的文档主题来放置项目的各种相关文档。最终找到这次的主角:Lotus Docs 基于Hugo的主题。Lotus Docs的样子&…...
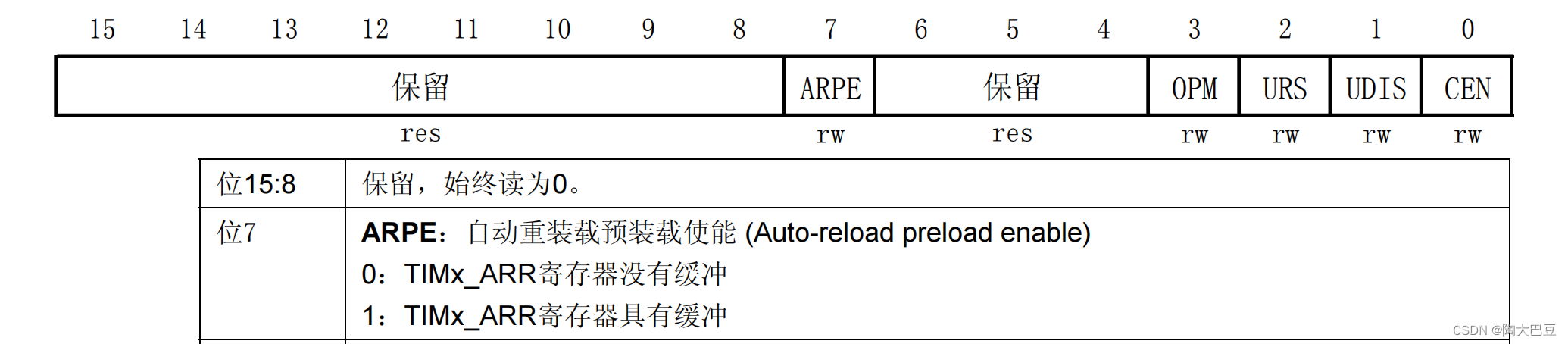
stm32---基本定时器(TIM6,TIM7)
STM32F1的定时器非常多,由两个基本定时器(TIM6,TIM7)、4个通用定时器(TIM2-TIM5)和两个高级定时器(TIM1,TIM8)组成。基本定时器的功能最为简单&am…...

HTML网页设计
HTML网页设计 HTML网页设计1、常用的单标签2、常用的双标签3、列表标签4、超链接标签5、图像和动画标签6、Html5中音频的插入7、定时刷新或跳转8、表格9、HTML表单标签与表单设计 HTML网页设计 属性值一般用" "括起来,且必须使用英文双引号 <head>…...

阶段性总结:跨时钟域同步处理
对时序图与Verilog语言之间的转化的认识: 首先明确工程要实现一个什么功能;用到的硬件实现一个什么功能。 要很明确这个硬件的工作时序,即:用什么样的信号,什么变化规则的信号去驱动这个硬件。 然后对工程进行模块划…...

[交互]接口与路由问题
[交互]接口与路由问题 场景描述问题分析解决方案 这是在实战开发过程中遇到的一个问题,所以导致产生了服务端如何区分浏览器请求的是前端路由还是 api 接口的问题?? 场景描述 这是一个前后端分离开发的项目,因此前端一般都会使用…...

linux 6中4T磁盘识别并分区格式化挂接
存储端划分4T的LUN后,主机端操作如下 1、主机识别,本例中hba卡的端口是host11和host12 [rootdb1 ~]# echo "- - -" > /sys/class/scsi_host/host11/scan [rootdb1 ~]# echo "- - -" > /sys/class/scsi_host/host12/scan …...
【Unity】ShaderGraph应用(浮动气泡)
【Unity】ShaderGraph应用(浮动气泡) 实现效果 一、实现的方法 1.使用节点介绍 Position:获取模型的顶点坐标 Simple Noise:简单的噪声,用于计算顶点抖动 Fresnel Effect:菲涅耳效应,用于实现气泡效果 计算用节点 Add&…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
